"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ"  N 2, 2006

оглавление

дискуссия

Математическое моделирование сферически-слоистого диэлектрического резонатора

 

|Моденов В.П.|, Гущин Р.А., Ерохин А.И., Шапкина Н.Е.
 

МГУ им. М. В. Ломоносова

 

Получена 4 апреля 2006 г.

 

 

1. Введение. 1

2. Постановка задачи. 2

3. Алгоритм решения характеристического уравнения. 4

4. Вычислительные результаты. 6

Литература.. 13

 

 

 

Рассмотрена математическая модель экранированного  сферического резонатора с многослойным диэлектрическим заполнением. На ее основе проведено исследование зависимости добротности резонатора от его геометрических и электродинамических параметров в случае  трехслойного заполнения.

 1. Введение.

Работа посвящена исследованию основной характеристики резонаторов – добротности. По сравнению с другими резонаторами простых конструкций сферический резонатор обладает более высокой добротностью [1]. На сегодняшний день среди них наилучшими с точки зрения добротности считаются сферические микро- и мини-резонаторы оптического диапазона частот на высокоазимутальных модах типа «шепчущей галереи». Благодаря современным технологиям [2], возможно создавать практически идеальные сферические резонаторы малых размеров с любым количеством диэлектрических слоев. Такие резонаторы могут использоваться для создания узкополосных фильтров, прецизионной измерительной аппаратуры, для стабилизации СВЧ-генераторов, а также в качестве чувствительных элементов для измерения различных физических и химических свойств окружающей среды. Таким образом, возникает интерес к исследованию зависимости добротности от количества слоев, геометрических и электродинамических параметров резонатора, от влияния экрана в случае экранированного резонатора. Последняя характеристика играет большую роль в связи с высокой нестабильностью открытых систем. Так в работе [3] был предложен и реализован алгоритм вычисления комплексных резонансных волновых чисел собственных колебаний сферического резонатора с заданным поверхностным импедансом. Были получены приближенные аналитические формулы для малого по модулю импеданса. Работа [4] посвящена исследованию собственных колебаний сферически-слоистого резонатора с импедансной поверхностью. В ней предлагается эффективный алгоритм нахождения волновых чисел собственных колебаний, и частично исследовано влияние различных параметров резонатора на его добротность. Было показано, что введением диэлектрического слоя и оптимальным выбором его геометрического расположения можно повысить добротность по отношению к полому сферическому резонатору. Настоящая работа является  развитием [4]. В ней приведено подробное описание алгоритма, исследована зависимость добротности от различных геометрических и электродинамических параметров экранированного резонатора в случае  трехслойного диэлектрического заполнения. В работе рассматриваются колебания электрического типа.

2. Постановка задачи.

Рассмотрим резонатор в виде  части пространства, ограниченной сферической поверхностью с заданным на ней комплексным  импедансом Z, и представляющей собой совокупность m концентрически расположенных шаровых слоев с заданными значениями диэлектрической проницаемости e_i. Магнитную проницаемость полагаем равной 1.

Рассмотрим данную систему в сферической системе координат (r,φ,q), совместив при этом начало координат с центром сферы.

Будем считать, что значения поверхностного импеданса и постоянных диэлектрических проницаемостей слоев не зависят от частоты электромагнитных колебаний.

Собственными колебания резонатора называют нетривиальные решения однородной краевой задачи для системы уравнений Максвелла

                           (1)

c граничными условиями Леонтовича-Щукина

и условиями сопряжения, заключающимися в требовании непрерывности касательных составляющих векторов напряженности  электрического и магнитного полей на границах диэлектрических слоев. Здесь  - единичный вектор внешней нормали к сфере, k – волновое число.

Систему (1) можно записать в виде

,

где  – диэлектрическая проницаемость s-го слоя диэлектрика,

 .

Компоненты решения данной системы представимы в виде

, , ,

 

, ,

с граничным условием

,

 где  потенциал Боргниса U_s удовлетворяет уравнению

.

Из условий сопряжения имеем:

После разделения переменных в характеристическом уравнении для потенциала Боргниса, получим:

, где  n – целое число.

Запишем решение в виде

 ,

где  и  - сферические функции Бесселя I и II рода n-го порядка соответственно, а и - некоторые постоянные.

После преобразований получаем систему дифференциальных уравнений

 где

Рассмотрим данную систему  как СЛАУ относительно неизвестных A₁,…, A_m, B₂,…, B_m. Число уравнений и переменных равно 2m-1, где m - число слоев.

Из условия существования нетривиального решения для СЛАУ получаем характеристическое уравнение для вычисления собственных значений k:

                                           (2)

3. Алгоритм решения характеристического уравнения.

Данное характеристическое уравнение решим с помощью бинарного итерационного корректор-процесса [5],  основанного на продолжении решения методом дифференцирования по параметру с уточнением решения методом Ньютона.

Заменим диэлектрические постоянные  на величины , где , t – параметр.  При t = 0 получаем задачу, заключающуюся в нахождении волнового числа k₁ для случая полого сферического резонатора с заданным поверхностным комплексным импедансом. Назовем ее задачей I. При t =1 получаем исходную задачу. Пусть  решение задачи I есть волновое число k₁. Считая простой комплексный корень k исходной задачи неявно заданной функцией параметра k =  k(t), получим задачу Коши:

 

             (3)

Таким образом, при известном значении k₁ решение исходной задачи представляет собой решение соответствующей задачи Коши, и мы приходим к более простой задаче I .

Заменим импеданс Z на величину uZ, где u – параметр. При u = 0 (величина t по-прежнему равна нулю) получаем задачу II для случая полого сферического резонатора с поверхностным импедансом равным нулю; при u = 1  получаем задачу I. Пусть k₂ есть решение задачи II.

Считая простой комплексный корень k₁ задачи I неявно заданной функцией параметра k₁ =  k₁ (u), получим задачу Коши:

  (4)

Таким образом, как и в предыдущем случае, при известном значении k₂ решение задачи I представляет собой решение задачи Коши. В итоге задача I свелась к еще более простой задаче II, заключающейся в нахождении волнового числа k₂ для случая полого сферического резонатора с нулевым импедансом на границе.

 Решим задачу II.

В этом случае решение задачи сводится к решению характеристического уравнения для определения волновых чисел колебания E_0np:

,               

Введем в это уравнение параметр g  и сделаем замену x = k₂r_m:

             

Считая корень этого уравнения x неявно заданной функцией параметра  и воспользовавшись дифференциально-полиномиальным свойством функции F(x) = :

,           

приходим к задаче Коши:

 

              (5)

где x₀ = x_np – p-ый корень уравнения .             

Используя дифференциально-параметрический метод [6] и считая корни уравнения

                 

известными, например= pπ (p = 1, 2, …), вычислим значения x_np , решая задачу Коши для дифференциального уравнения с производной по параметру:

               (6)

Таким образом, решение исходной задачи редуцировано к решению четырех выше указанных задач Коши (3)-(6). Они решались методом Рунге-Кутта четвертого порядка, при этом для задач I, II уточнение корня на каждом шаге проводилось методом Ньютона по формуле

   

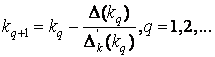
Физической интерпретацией решения является последовательное введение в идеальный полый сферический резонатор (импеданс равен нулю) потерь (когда импеданс отличен от нуля), затем постепенное заполнение диэлектрическими слоями.

Для вычисления зависимости волнового числа от каких-либо других характеристик резонатора, к примеру, от  расположения экрана, к ним применяется введение параметра, аналогичное приведенному выше для задач I, II. 

4. Вычислительные результаты.

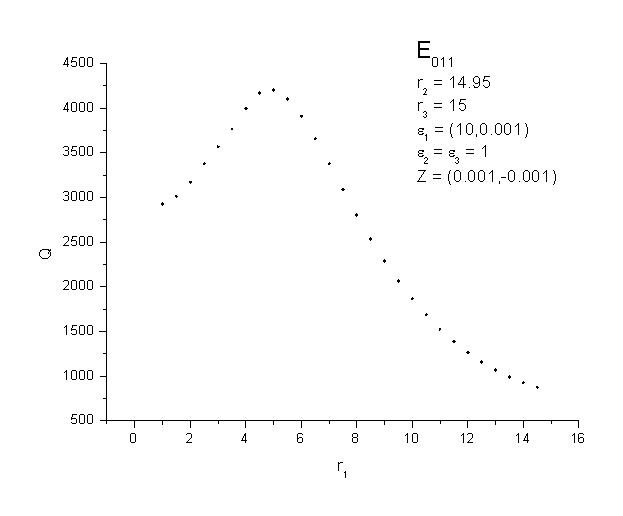
Важнейшей характеристикой экранированного резонатора является влияние экрана на добротность. Рассмотрим сначала экран с потерями. Было обнаружено, что при определенных геометрических параметрах заполнения сферического однослойного резонатора существует оптимальное расположение экрана, при котором добротность максимальна. При дальнейшем увеличении расстояния от экрана до диэлектрика добротность понижается и впоследствии уже практически не меняется (рис.1). Таким образом, для увеличения добротности нет необходимости сильного удаления экрана, вследствие чего значительно сокращаются размеры резонаторов, что очень важно в их современном практическом применении.

 

Рис.1

 

Пусть теперь размеры резонатора ограничены, то есть положение  импедансного экрана фиксировано. Введем в резонатор концентрический шаровой диэлектрик и будем постепенно увеличивать его размеры, пока радиус последнего не приблизится к радиусу  экрана. В этом случае также существует оптимальное заполнение экрана (рис 2), при котором добротность максимальна.

 

Рис. 2

Добротность также может быть повышена благодаря использованию колебаний типа шепчущей галереи, так как вычисления показали, что с ростом полярного индекса n добротность значительно возрастает (рис 3).

                                                    

Рис. 3

 

 

При увеличении радиального индекса p увеличивается число резонансных положений экрана, причем их число совпадает с номером этого индекса (рис. 4,5).  Добротность также увеличивается. Таким образом, при фиксированных параметрах резонатора с помощью выбора мод с высокими радиальным и полярным индексами возможно значительно улучшить добротность резонатора (рис. 6, сравни с рис.4).

 

Рис. 4

 

Рис. 5

Рис. 6

В случае резонатора с параметрами  при фиксированном положении экрана существует оптимальное положение диэлектрика (рис 3). Показано, что использование диэлектриков с малыми потерями приводит к большей добротности.

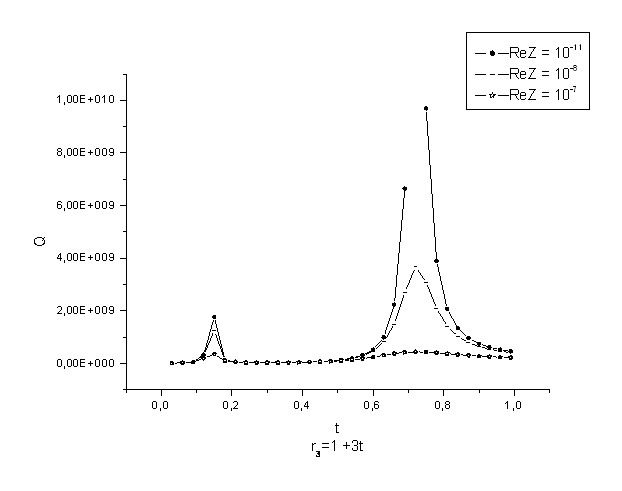
Уменьшая потери в экране можно добиться добротности, обусловленной в основном фундаментальными потерями в диэлектрике. Так в случае идеального экрана при  при определенных параметрах резонатора для колебания Е₁₀₂ была получена добротность равная 10¹⁰ (рис. 7). Это было достигнуто уменьшением толщины слоя и  потерь в нем, что повышает добротность, а также выбором оптимального положения экрана. При удалении экрана было обнаружено два максимума, причем дальний из них по отношению к диэлектрику значительно превосходит ближний по добротности. При введении небольших потерь в экран картина качественно сохраняется.

 

Рис. 7

Были получены результаты, согласующиеся с общими физическими соображениями. К примеру, рассмотрим резонатор с двухслойным сферическим заполнением. Экран и размеры внутреннего диэлектрика фиксированы.  Будем увеличивать размеры внешнего диэлектрика. При этом наблюдается уменьшение добротности (рис. 8). Действительно, если рассматривать внешний диэлектрик как некоторый слой, загрязняющий  резонатор, то увеличение его размеров будет соответствовать увеличению потерь резонатора.

Результаты расчетов согласуются с данными, полученными другими методами [7].

Рис. 8

 

Литература

 

1.     Ильинский А.С., Слепян Г.Я. Колебания и волны в электродинамических системах с потерями.- М.: Изд-во МГУ, 1983.

2.     Sadayuki Ueha. “Ultrasonic actuators using near-field acoustic levitation”. Session ULTRASONIC ACTUATION AND LEVITATION. 1998 IEEE INTERNATIONAL ULTRASONICS SYMPOSIUM, Sendai, Miyagi, JAPAN, October 5-8, 1998.

3.     Моденов В.П. // Радиотехника и электроника, 2000. Т. 45. N 10. – С. 1198.

4.     Моденов В.П., Чулков Ф.М. // Электродинамика и техника СВЧ и КВЧ, 2000. Т. 8. N 3-4 (28).- С. 89.

5.     Моденов В.П. // Вестник МГУ. Сер. 15: Вычислительная математика и кибернетика, 1985. N 2.- С. 63.

6.     Моденов В.П. // Докл. АН СССР. 1987. Т. 296. N 3.- С.536.

7.    Krupka, J.; Tobar, M.E.; Hartnett, J.G.; Cros, D.; Le Floch, J.-M.;  Extremely high-Q factor dielectric resonators for millimeter-wave applications Microwave Theory and Techniques, IEEE Transactions,  Volume:53 , Issue: 2 , Feb. 2005. P.702