УДК 621.396:621.391.82
Алгоритм
неградиентной коррекции радиолокационных изображений при траекторных искажениях
фазы сигнала в РСА
О. В. Сытник
Институт радиофизики и электроники им. А.Я. Усикова НАН Украины
Получена 26 марта 2008 г.
Рассматриваются задачи построения адаптивных алгоритмов синтезирования радиолокационных изображений подстилающей поверхности по сигналам когерентного бортового радиолокатора. Предложенный алгоритм относится к классу самонастраивающихся алгоритмов, в которых информация о траекторных ошибках извлекается непосредственно из отраженного сигнала. В качестве информационных параметров используется усредненная по наклонной дальности оценка смещения доплеровского спектра на интервале синтезирования и ее высшие производные. Это обеспечивает возможность автоматической коррекции изображений, обусловленных не только ошибками по скорости полета носителя, но позволяет учесть ошибки, вызванные неучтенным ускорением и скоростью изменения ускорения. Поиск оптимального в смысле минимума среднего квадрата ошибки корректирующего множителя опорной функции осуществляется неградиентным случайным поиском. Приведены результаты обработки сигналов когерентного радиолокатора с синтезированием апертуры антенны (РСА). Обсуждаются особенности работы алгоритма в различных условиях.
Введение.
Бортовые радиолокационные станции с синтезированием апертуры антенны (РСА) формируют радиолокационное изображение (РЛИ) местности путем когерентной обработки отраженных от подстилающей поверхности сигналов. Принцип синтезирования основан на перемещении бортовой антенны РЛС для последовательного формирования антенной решетки больших размеров на траектории полета [1–2]. Амплитуда и фаза отраженного от подстилающей поверхности колебания, регистрируемого приемным устройством вдоль траектории полета носителя РСА, содержит информацию об участках местности и объектах на ней. Такой принцип землеобзора эффективно используется в РСА космического и самолетного базирования для решения важных научных и практических задач. При этом радиолокационные изображения местности при цифровой обработке можно оперативно получать непосредственно на борту носителя с высоким пространственным разрешением.
Отклонения от заданной траектории полета носителя РСА, которые не учтены в алгоритме обработки сигнала в виде соответствующих корректирующих функций, приводят к искажениям результирующего радиолокационного изображения. В частности, это расфокусировка по азимутальной и дальностной координатам, смещение объектов относительно их истинного положения, потеря яркости изображения, увеличение боковых лепестков синтезированной диаграммы направленности, что влечет за собой повторы целей, и ряд других искажений. Поэтому для получения радиолокационных изображений приемлемого качества приходится ограничивать интервал синтезирования или применять различные методы компенсации траекторных ошибок.
Коррекция траекторных ошибок при синтезировании апертуры в РСА осуществляется на основе целого ряда различных методов [3–8]. Всю совокупность методов можно разделить на три группы:
¾ методы, использующие информацию о положении носителя в каждой точке его траектории от специальных бортовых датчиков различного типа;
¾ методы, использующие информацию об отклонении реальной траектории полета от расчетной, извлеченную из траекторного сигнала;
¾ комбинированные методы.
Создание радиолокационной аппаратуры, инвариантной к типу и характеристикам бортовых навигационных средств и одновременно обеспечивающей автоматическую коррекцию радиолокационных изображений, возможно благодаря извлечению информации о траекторных ошибках непосредственно из отраженного сигнала.
Постановка задачи.
В общем виде алгоритм формирования синтезированной апертуры в азимутальном направлении для фиксированной дальности можно представить в виде интеграла свертки [1]
где ![]() - операция вычисления модуля;
- операция вычисления модуля; ![]() - интервал времени, в течении которого
выполняется синтезирование апертуры антенны;
- интервал времени, в течении которого
выполняется синтезирование апертуры антенны; ![]()
![]() - аддитивная смесь отраженного от
подстилающей поверхности сигнала
- аддитивная смесь отраженного от
подстилающей поверхности сигнала ![]() ;
; ![]() - амплитуда отраженного сигнала;
- амплитуда отраженного сигнала; ![]() - текущее значение
наклонной дальности от фазового центра передающей антенны до
- текущее значение
наклонной дальности от фазового центра передающей антенны до ![]() -го точечного
отражателя;
-го точечного
отражателя; ![]() -
длина волны зондирующих колебаний (без потери общности множитель
-
длина волны зондирующих колебаний (без потери общности множитель ![]() в этом выражении
опущен) и некогерентного гауссовского шума
в этом выражении
опущен) и некогерентного гауссовского шума ![]() с дисперсией
с дисперсией ![]() и нулевым математическим ожиданием;
и нулевым математическим ожиданием; ![]() - опорная функция, где
- опорная функция, где ![]() - весовая функция,
которая в простейшем случае может быть
- весовая функция,
которая в простейшем случае может быть ![]() ;
; ![]() - путевая скорость движения носителя РСА.
- путевая скорость движения носителя РСА.
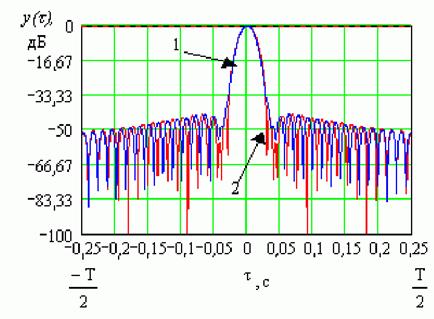
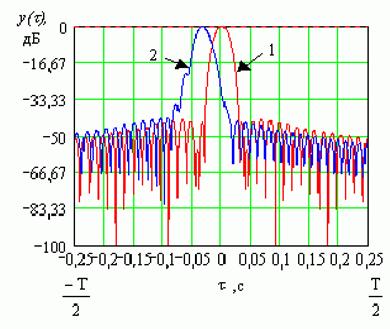
В результате работы алгоритма (1) при условии отсутствия траекторных ошибок формируется диаграмма направленности (ДН) эквивалентной антенны, показанная на рис.1, кривая 1. Кривая 2 рис.1 иллюстрирует характер искажений, возникающих при нестационарном движении летательного аппарата, изменения параметров движения которого не учтены в опорной функции при синтезировании по алгоритму (1). Как видно из рис.1, ошибки в определении путевой скорости приводят к смещению максимума синтезированной ДН, т.е. к появлению ошибок целеуказания.
Рис.1. Синтезированные ДН антенны РСА при отсутствии траекторных ошибок (кривая 1) и при наличии ошибок по путевой скорости и ускорению.
Ошибки в определении
ускорения и скорости изменения ускорения приводят к увеличению ширины главного
лепестка синтезированной антенны (что эквивалентно потере разрешающей
способности РСА в азимутальном направлении), повышению уровня боковых лепестков
и асимметрии главного лепестка. На радиолокационном изображении такого рода
траекторные ошибки проявляются в виде геометрических искажений, повторов,
пятнистости, потере потенциала локатора, что, в свою очередь, приводит к искажениям
контрастов отдельных участков и расфокусировке изображения в целом. При
формировании обеих диаграмм использовалась опорная функция с весовым окном
Хэмминга [9].
Информационный сигнал.
Характер изменения
траекторного сигнала на интервале синтезирования ![]() при облучении бортовым локатором точечной
цели подчиняется закону линейного частотно-модулированного колебания с круговой
частотой
при облучении бортовым локатором точечной
цели подчиняется закону линейного частотно-модулированного колебания с круговой
частотой ![]() .
При
.
При ![]() закон
изменения частоты сигнала в пределах главного лепестка реальной ДН есть
линейная функция, а огибающая его спектра ¾ симметрична относительно центрального элемента
массива отсчетов траекторного сигнала и монотонно убывает с увеличением частоты
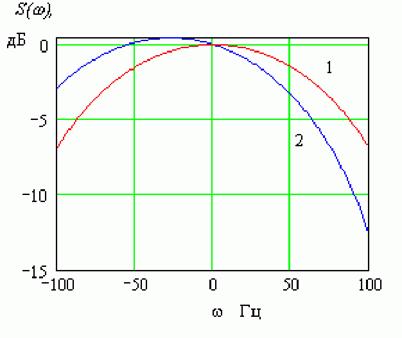
(как показано на рис.2, кривая 1). Ошибки в определении параметров движения
носителя РСА приводят к искажениям формы спектральной плотности, в частности, к
ее асимметрии относительно середины распределения (кривая 2, рис.2). Поэтому
кажется перспективным использование отличия формы реального спектра сигнала от
идеального путем введения соответствующих корректирующих составляющих в опорную
функцию алгоритма синтезирования (1).
закон
изменения частоты сигнала в пределах главного лепестка реальной ДН есть
линейная функция, а огибающая его спектра ¾ симметрична относительно центрального элемента
массива отсчетов траекторного сигнала и монотонно убывает с увеличением частоты
(как показано на рис.2, кривая 1). Ошибки в определении параметров движения
носителя РСА приводят к искажениям формы спектральной плотности, в частности, к
ее асимметрии относительно середины распределения (кривая 2, рис.2). Поэтому
кажется перспективным использование отличия формы реального спектра сигнала от
идеального путем введения соответствующих корректирующих составляющих в опорную
функцию алгоритма синтезирования (1).
Рис.2. Идеализированная форма огибающей спектра доплеровских частот при отсутствии (кривая 1) и наличии (кривая 2) траекторных ошибок.
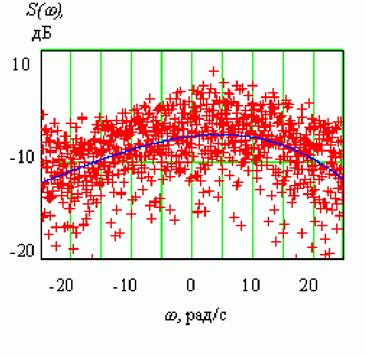
Амплитудный спектр доплеровских частот реального сигнала, отраженного от различных по масштабу и радиофизическим свойствам элементов подстилающей поверхности, носит флуктуационный характер, и его непосредственное использование для построения корректирующей опорной функции затруднительно. На рис.3 показан усредненный по 128-ми соседним стробам наклонной дальности спектр траекторного сигнала на участке траектории, где летательный аппарат совершал маневр.
Рис.3. Спектральная плотность доплеровских частот траекторного сигнала при маневре носителя РСА (показана символами +) и ее полиномиальная аппроксимация полиномом третьей степени (сплошная линия).
Алгоритм коррекции.
Из-за значительной дисперсии отсчетов огибающей спектра построить формализованную процедуру вычисления достоверных оценок величин смещения и коэффициентов асимметрии для получения корректирующих составляющих опорной функции затруднительно. Однако, если полученные из реальной последовательности спектральные отсчеты аппроксимировать известной функцией, например полиномом, то процедура вычисления корректирующих коэффициентов опорной функции легко формализуется. На рис.3 символом "+" показаны спектральные отсчеты траекторного сигнала, а сплошной линией ¾ его полиномиальная аппроксимация полиномом третьей степени с коэффициентами: 24,469; 0,024; 1,656 * 10-5; -4,507 * 10-8. Коэффициенты полинома вычислялись из системы уравнений
где ![]() ;
; ![]() –степень аппроксимирующего полинома;
–степень аппроксимирующего полинома; ![]() – соответствующий
индексу коэффициент полинома;
– соответствующий
индексу коэффициент полинома;![]() –базисная функция. При условии минимума
величины нормированной среднеквадратичной погрешности аппроксимации
–базисная функция. При условии минимума
величины нормированной среднеквадратичной погрешности аппроксимации
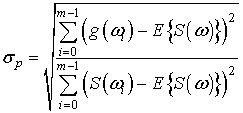 ,
,
где ![]() ¾ символ операции вычисления математического ожидания.
¾ символ операции вычисления математического ожидания.
Достигнутая в этой процедуре ![]() не превышала 0,248.
не превышала 0,248.
Кроме того, если предположить, что инерционный летательный аппарат, на котором установлен РСА, не может совершать быстрых по отношению к интервалу синтезирования изменений своего положения, а высокочастотные составляющие спектра флуктуаций фазового центра антенны, обусловленные вибрациями корпуса носителя незначительны, то в разложении в ряд Маклорена [10] показателя экспоненты в выражении для опорной функции можно оставить не более трех составляющих [6]. Тогда, мгновенное значение наклонной дальности r(t) от фазового центра антенны РСА до отражателя на поверхности может быть представлено как:
Используя представление
(3), нетрудно рассчитать проекции фазовых ошибок в опорной функции для смещений
носителя вдоль координат ![]() , где координата
, где координата ![]() совпадает с направлением полета
носителя, координата
совпадает с направлением полета
носителя, координата ![]() -
с направлением перпендикулярным направлению полета и координата
-
с направлением перпендикулярным направлению полета и координата ![]() - с нормалью к поверхности
земли.
- с нормалью к поверхности
земли.
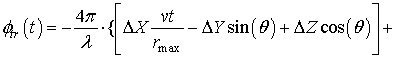
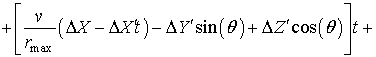 (4)
(4)
где DX, DY, DZ – ошибки положения носителя соответственно вдоль линии полета, поперек линии полета и по высоте; DX', DY', DZ', DX'', DY'', DZ'' – соответствующие производные этих ошибок; v -начальная скорость в момент времени t.; q-угол между нормалью, опущенной из фазового центра антенны к подстилающей поверхности и направлением на цель.
Фазовую ошибку, обусловленную совместной неоднозначностью по некомпенсированному углу сноса и положения носителя РСА на орбите (под ошибками положения носителя понимаются ошибки положения фазового центра реальной антенны) определим как ряд
где b, b', b'' ¾ соответственно угол сноса, скорость изменения угла сноса и ускорение изменения угла сноса. А фазовую ошибку, обусловленную совместной неоднозначностью по некомпенсированному углу q между нормалью и направлением излучения, а также положения носителя РСА на орбите по высоте и направлению перпендикулярному линии полета, можно записать в виде
![]()
![]()
Без потери общности предположим, что все параметры движения носителя РСА (за исключением его путевой скорости) известны со сколь угодно высокой точностью, то фазовые ошибки, связанные с неадекватным представлением закона изменения путевой скорости, можно представить в упрощённом виде и изучать их влияние на характеристики РЛИ отдельно от ошибок (4)-(6)
где Dv, a, a' - ошибки измерения путевой скорости, ускорения и производной от ускорения соответственно.
Корректирующие фазу опорной функции (1) коэффициенты Dv, a, a' найдем из сравнения кривых 1 и 2
рис.2. Причем в качестве кривой 2 необходимо использовать модель
аппроксимирующей функции, показанной на рис.3. Коэффициент Dv, физический смысл которого – ошибка в определении
путевой скорости, определим путем отыскания смещения экстремума кривой 2 по
отношению к эталонной кривой 1. Формализовать эту процедуру для алгоритма
автоматической коррекции фазы опорной функции можно при помощи, например,
метода неградиентного случайного поиска [11]. Обозначим искомую ![]() и искаженную
и искаженную ![]() спектральные плотности в
виде векторов размером
спектральные плотности в
виде векторов размером ![]() , где
, где ![]() ─ число дискретных отсчетов функции в
спектральной области, которое равно количеству зондирующих импульсов на
интервале синтезирования. В общем виде алгоритм неградиентного случайного
поиска имеет следующую структуру
─ число дискретных отсчетов функции в
спектральной области, которое равно количеству зондирующих импульсов на
интервале синтезирования. В общем виде алгоритм неградиентного случайного
поиска имеет следующую структуру
где 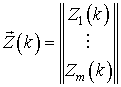 ─ вектор случайных чисел размера
─ вектор случайных чисел размера ![]() , а
, а 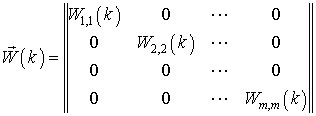 ─ квадратная матрица, на
диагонали которой размещаются положительные случайные числа, свойства которых
изменяются от
─ квадратная матрица, на
диагонали которой размещаются положительные случайные числа, свойства которых
изменяются от ![]() ,
знак
,
знак ![]() относится
к каждому элементу вектора
относится
к каждому элементу вектора ![]() .
.
Требования к случайным
последовательностям, обеспечивающим сходимость ![]() к
к ![]() с вероятностью 1 подробно описаны в [11].
с вероятностью 1 подробно описаны в [11].
Результаты эксперимента.
Для случая, показанного на рис.1, процедура (8) формирует ДН РСА показанную на рис.4 за 36 итераций.
Рис.4. Исправленная ДН РСА (кривая 1), эталонная ДН РСА (кривая 2).
Как видно из рис.4, в области главного лепестка ДН
кривые 1 и 2 полностью совпадают. Остаточная ошибка аппроксимации, обусловленная
ошибками определения корректирующих коэффициентов, проявляется в области
боковых лепестков на уровнях ниже минус 50дБ, что для подавляющего большинства
прикладных задач достаточно. Эффект от применения адаптивной коррекции изображения,
которое получено при синтезировании из голограммы самолетного радиолокатора
дециметрового диапазона (![]() м.), виден при сравнении изображений на
рис.5 и рис.6.
м.), виден при сравнении изображений на
рис.5 и рис.6.
Рис.5. Фрагмент синтезированного радиоизображения местности при маневре летательного аппарата.
На рис.5 ¾ 8 азимутальное направление показано сверху-вниз, а по наклонной дальности ¾ слева-направо. Разрешение по наклонной дальности дециметрового локатора 22,5 м, а по азимуту примерно 10 м.
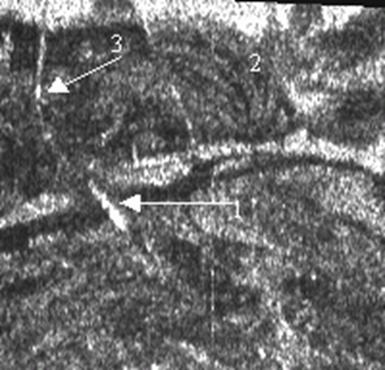
Рис.6. Фрагмент синтезированного радиоизображения местности при маневре летательного аппарата и адаптивной компенсации траекторных ошибок.
В частности, в результате применения адаптивной коррекции радиоизображения повтор объекта 1 на рис.5 и 6 отсутствует. Периодическая структура, отмеченная цифрой 2 на обоих рисунках, осталась практически без изменения. При вычислении корректирующих коэффициентов использовалась спектральная оценка, показанная на рис.3.
На рис. 7 и 8 показано применение адаптивной коррекции
изображения когерентного самолетного локатора метрового диапазона длин волн (![]() м.). Элемент разрешения
для изображений рис.7 и 8 составляет 15х37.5 м.
м.). Элемент разрешения
для изображений рис.7 и 8 составляет 15х37.5 м.
Рис.7. Фрагмент радиоизображения местности без коррекции.
Отклики периодической структуры, обозначенные на рис.7 цифрой 1, на участке, где самолет изменял параметры полета, размазаны в азимутальном направлении. На рис.8 показан этот же участок местности при синтезировании с алгоритмом адаптивной коррекции параметров полета. Как видно из рис.8, отклики от целей на участке 1 приняли форму, аналогичную откликам на участке 2. Кроме того, яркие сплошные линии, представляющие собой отклики от лесополос, прорисованы на рис.8 с более высокой детализацией чем на рис.7.
Рис.8. Фрагмент радиоизображения местности после обработки алгоритмом с коррекцией траекторных ошибок.
Кроме визуальной оценки синтезированных изображений подстилающей поверхности в качестве оперативного критерия можно предложить сравнительный анализ радиолокационных контрастов вдоль строки записи сигнала на протяжении всего сеанса работы. (Здесь под строкой понимается запись траекторного сигнала вдоль линии полета.) Так, на рис. 9 показан результат синтезирования одной строки с учетом коррекции траекторных ошибок и на рис. 10 ¾ стандартным алгоритмом прямой свертки.
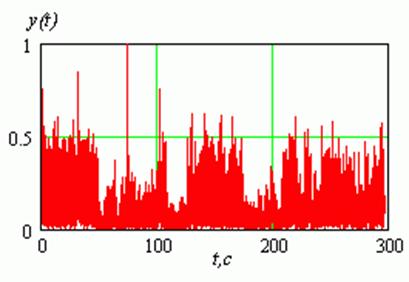
Рис.9. Результат синтезирования 208-го строба дальности дециметрового локатора с учетом коррекции траекторных ошибок.
Для удобства сравнения масштаб амплитуд откликов от целей по оси ординат на рис.9 и рис.10 линейный, и амплитуды откликов нормированы к максимуму на рис.9. Общее время записи составляло 300 с при скорости самолета 487 км/час.
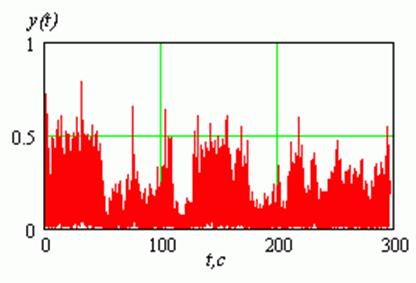
Рис.10. Результат синтезирования 208-го строба дальности дециметрового локатора стандартным алгоритмом.
Наклонная дальность до выбранного строба составляла 13680 м, а интервал синтезирования ¾ 1,8 с. Применение алгоритма адаптивной коррекции практически на всем протяжении полета приводит к увеличению радиолокационных контрастов на 10 – 20 %, а по отдельным целям (например рис.9, цель в интервале между 70 и 90 с полета) амплитуда отклика от одиночной цели возрастает почти 1,5 раза.
Выводы. Процедура обработки искаженных участков радиоизображений подстилающей поверхности состоит в том, что исходная когерентная запись траекторного сигнала подвергается предварительному Фурье анализу, и одновременно отсчеты траекторного сигнала сохраняются в элементах памяти. В частности, при создании спецпроцессоров бортовой обработки РСА сигналов это могут быть сдвиговые регистры, а при наземной – накопители на жестких дисках, имеющие соответствующий объем памяти. Затем с целью снижения дисперсии флуктуационной составляющей спектральных отсчетов выполняется усреднение по нескольким соседним стробам дальности. По полученной таким образом спектральной оценке вычисляют корректирующие коэффициенты для опорной функции. Выбор алгоритма неградиентного случайного поиска обусловлен тем, что скорость адаптации и результирующая остаточная ошибка аппроксимации практически не зависят от участка полосы обзора (имеется ввиду ближний или дальний по отношению к надиру край полосы).
Как показала практика, применение адаптивного алгоритма синтезирования позволяет повысить амплитуду отклика от отражателей на поверхности до 1,5 раз и повысить разрешающую способность на отдельных участках почти вдвое по сравнению с традиционным (неадаптивным) алгоритмом синтезирования. Для представленных в работе реальных записей сигнала алгоритм аппроксимации давал приемлемые в смысле визуального качества коррекции изображений оценки смещений скорости и ускорения за 30–40 итераций.
Литература
1. Радиолокационные станции с цифровым синтезированием апертуры антенны / Под ред. В.Т. Горяинова – М.: Радио и связь, 1988 – 304с.
2. Томиясу К.. Радиолокационные станции с синтезированием апертуры и их применение для отображения поверхности океана // Тр. ин-та инж. по электротехнике и радиоэлектронике. - 1978. - 66, № 5. – С.40 – 67.
3. Ицхоки Я.С., Сазонов Н.А., Толстов Е.Ф. Основные характеристики РСА при произвольном движении летательного аппарата // Радиотехника и электроника. - 1984.-29, №11. –С.2164-2172.
4. Hounam D. Motion Errors and Compensation Possibilities // AGARD Lecture Series 182. Fundamentals and Special Problems of Synthetic Aperture Radar (SAR). -1992. – P. 31 – 42.
5. Moreira J.A. A New Method of Aircraft Motion Error Extraction from Radar Raw Data for Real Time SAR Motion Compensation. // Proc., IGARSS Symposium, Vancover< Canada. -1999. – Р. 1- 7.
6. Сытник О.В., Кабанов А.В., Ефимов В.Б. и др. Критерий качества радиолокационного изображения когерентных систем дистанционного зондирования // «Космічна наука і технологія». :Тез. Докл. 2002.- 8, №2/3. – С.287 – 288.
7. Cumming I., Wong F., Hawkins R. RADARSAT-1 Doppler Centroid Estimation Using Phase Based Estimators // Proc., IGARSS Symposium, -2002. – Р. 1-3.
8. Sharif A. H. A., Cumming I. Centroid Estimation for Azimuth-Offset SARs // Proceedings of the IEEE National Aerospace and Electronics Conference, NAECON'95,- 1995, Dayton, Ohio, May 22-26,- P. 134-139.
9. Марпл С.Л. Цифровой спектральный анализ и его приложения / Пер. с англ. Под ред. С.И. Рыжака– М.: Мир, 1990. – 584 с.
10. Бронштейн И.Н., Семендяев К.А. Справочник по математике. – М.: Наука, 1981. – 720 с.
11. Гладков Д.И. Оптимизация систем неградиентным случайным поиском. ─ М.: Энергоатомиздат, 1984. ─ 256 с.
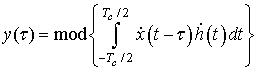
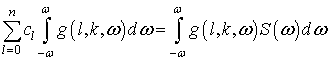 , (2)
, (2)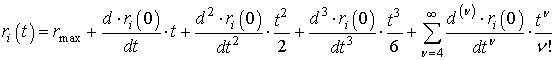 . (3)
. (3)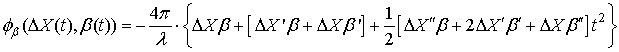
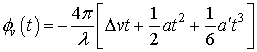 ,
(7)
,
(7)