УДК 621.372.852; 621.318.134.029.64
НЕЛИНЕЙНЫЕ
МАГНИТОСТАТИЧЕСКИЕ ВОЛНЫ В СЛОИСТЫХ СТРУКТУРАХ НА ОСНОВЕ ФЕРРОМАГНИТНЫХ ПЛЁНОК
М.А. Малюгина, Ю.П. Шараевский
Саратовский государственный университет им. Н.Г. Чернышевского
Получена 23 апреля 2008 г.
Теоретически показана возможность модуляционной неустойчивости поверхностных магнитостатических волн относительно возмущений вдоль направления распространения в связанной касательно намагниченной ферромагнитной структуре с металлическими экранами, как при возбуждении одной моды в структуре за счёт изменения характера дисперсии, так и при возбуждении двух мод за счёт возникновения нелинейной связи.
Известно (см., например, [1-4]), что поверхностные магнитостатические волны (ПМСВ), распространяющиеся в одиночной касательно намагниченной ферромагнитной плёнке[1], при повышении уровня сигнала являются устойчивыми относительно продольных возмущений, т.е. для такого типа волн отсутствует модуляционная неустойчивость в направлении распространения возмущения. В тоже время в слоистых структурах, например, типа феррит-полупроводник [5] или феррит-диэлектрик-металл [6], введение дополнительного слоя (полупроводника или металла) может приводить при определённых условиях к модуляционной неустойчивости ПМСВ, причём этот эффект обусловлен, в основном, изменением характера дисперсии волн. Модуляционная неустойчивость ПМСВ в одиночной ферромагнитной плёнке может наблюдаться также при возбуждении двух сигналов на разных частотах, причём в данной ситуации неустойчивость обусловлена взаимным влиянием двух модуляционно устойчивых волн [7,8].
Использование связи значительно расширяет функциональные возможности электродинамических систем [3-6]. Особенности влияния связи на нелинейные процессы самовоздействия, такие как образование уединённых волн (солитонов) огибающей, автомодуляцию амплитуды огибающей, применительно к случаю распространения связанных объёмных магнитостатических волн (ОМСВ) в нормально намагниченной структуре подробно рассмотрены в работах авторов [9,10]. Причём показано, что в таких системах связь может не только приводить к изменению дисперсионных характеристик волн, но и к появлению нелинейной связи между волнами (см. также [11-12]). Что касается ПМСВ, то в работе [11] теоретически показана возможность модуляционной неустойчивости ПМСВ в связанной структуре из двух ферромагнитных плёнок, разделённых тонким слоем диэлектрика в узкой области частот при возбуждении одной, быстрой или медленной моды в структуре. Данный эффект связан с изменением характера дисперсии ПМСВ и появлением областей с положительной дисперсией на дисперсионных характеристиках быстрой и медленной волн в связанной структуре. Крое того, показано, что независимо от того, наблюдается ли модуляционная неустойчивость в одиночной плёнке, МСВ в связанной структуре всегда является модуляционно неустойчивой при одновременном возбуждении двух волн. [10,11,12]. Модуляционная неустойчивость, возникающая при одновременном распространении двух модуляционно устойчивых волн, связанных через нелинейность, получила названием кросс-модуляции [12, 13].
Кроме того, распространение ПМСВ сильно зависит от граничных условий (использование металлических экранов в структуре, плёнок с различными характеристиками и т.д.) [4]. Например, если плёнки в структуре разной намагниченности, то частотные полосы пропускания нормальных мод разные, и в этом случае, в зависимости от частоты сигнала и от соотношения параметров, в структуре можно возбудить либо одну, либо две моды [1,14]. Поверхностные МСВ чрезвычайно чувствительны к металлическим нагрузкам (экранам). Наличие металлических экранов позволяет получать любой вид дисперсии МСВ – нормальную аномальную, линейную зависимость и пр., а также даёт возможность управлять полосой передачи, изменяя её в широких пределах. Использование связанных ПМСВ ещё более расширяет возможности управления их характеристиками. Изменение дисперсии волн, очевидно, приведёт к изменению характера модуляционной неустойчивости и основных характеристик нелинейных процессов самовоздействия. Данная работа посвящена исследованию влияния граничных условий, в частности металлических экранов, на характер модуляционной неустойчивости ПМСВ в таких структурах.
Анализируемая в работе структура, представляет собой два
тонких ферромагнитных слоя 1 и 2 толщиной ![]() и с намагниченностью насыщения
и с намагниченностью насыщения ![]() , соответственно, разделенных
диэлектрическим промежутком толщины
d, каждая из которых нагружена
металлическим экраном, расположенным на расстоянии
L от плёнки (рис.1). Структура
бесконечна в направлении осей x и y, постоянное магнитное поле
, соответственно, разделенных
диэлектрическим промежутком толщины
d, каждая из которых нагружена
металлическим экраном, расположенным на расстоянии
L от плёнки (рис.1). Структура
бесконечна в направлении осей x и y, постоянное магнитное поле ![]() приложено по касательной
к поверхности слоёв.
приложено по касательной
к поверхности слоёв.
Рис. 1. Схематическое изображение исследуемой модели.
Предполагается [9,10], что взаимное
влияние магнитостатических волн в каждой из плёнок осуществляется через
высокочастотные магнитные поля (связь носит чисто электродинамический характер),
что позволяет в уравнениях движение для вектора намагниченности и уравнениях
магнитостатики, записанных для каждого слоя 1 и 2, эффективные магнитные поля ![]() в каждом слое
представить следующим образом:
в каждом слое
представить следующим образом:
где ![]() - переменные ВЧ магнитные поля,
- переменные ВЧ магнитные поля, ![]() - постоянные
компоненты,
- постоянные
компоненты, ![]() -
коэффициент связи между слоями. Значение
-
коэффициент связи между слоями. Значение ![]() можно рассчитать на основе линейной теории
(см., например, [9,10]) и тогда
можно рассчитать на основе линейной теории
(см., например, [9,10]) и тогда ![]() , где k - постоянная
распространения волны в системе.
, где k - постоянная
распространения волны в системе.
Допустим
также, что нелинейность каждой плёнки определяется только величиной переменной
намагниченности этой плёнки, т.е. нелинейность, обусловленная изменением продольной
компоненты магнитного момента ![]() , для каждого слоя задаётся в виде [4]:
, для каждого слоя задаётся в виде [4]:
где ![]() – переменные
намагниченности, значения которых определяются ВЧ магнитными полями как одной,
так и другой плёнки.
– переменные
намагниченности, значения которых определяются ВЧ магнитными полями как одной,
так и другой плёнки.
Важной особенностью связанных структур является расщепление
дисперсионной кривой, соответствующей волне в одиночной плёнке, на две, т.е. возбуждение
на одной частоте w
двух нормальных волн – быстрой (с амплитудой ![]() ) и медленной волн (
) и медленной волн (![]() ) с различными волновыми числами kб,м. Если плёнки в
структуре различные, то поведение дисперсионных кривых в этом случае имеет ряд
особенностей. Например, если плёнки в структуре имеют разную намагниченность,
то полосы пропускания быстрой и медленной волн могут не совпадать [4].
) с различными волновыми числами kб,м. Если плёнки в
структуре различные, то поведение дисперсионных кривых в этом случае имеет ряд
особенностей. Например, если плёнки в структуре имеют разную намагниченность,
то полосы пропускания быстрой и медленной волн могут не совпадать [4].
Дисперсионное уравнение, описывающее связанные поверхностные магнитостатические волны, имеет следующий вид [4]:
где  ,
,
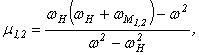
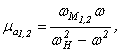
![]() ,
, ![]() H0,
H0, ![]() - гиромагнитная постоянная.
- гиромагнитная постоянная.
С учётом соотношений (1) и (2) можно получить нелинейные дисперсионные соотношения для быстрой и медленной волн в линиях, с использованием которых на основе метода огибающих [2] была получена следующая система нелинейных уравнений, описывающих эволюцию огибающей сигнала[2]:
где ![]() ,
,  ,
, 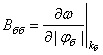 ,
, 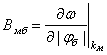 ,
, 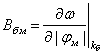 ,
, 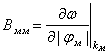 - коэффициенты, характеризующие групповые
скорости, дисперсию и нелинейность быстрой и медленной волны, соответственно, и
зависящие от параметров плёнок и величины связи. Комплексные
амплитуды волн в каждой из плёнок
- коэффициенты, характеризующие групповые
скорости, дисперсию и нелинейность быстрой и медленной волны, соответственно, и
зависящие от параметров плёнок и величины связи. Комплексные
амплитуды волн в каждой из плёнок ![]() , где k1,2 – постоянные распространения в плёнках)
связаны соотношениями
, где k1,2 – постоянные распространения в плёнках)
связаны соотношениями ![]() , где N и R1,2 коэффициенты,
значение которых определяются относительными параметрами плёнок (если плёнки
одинаковые, то N=R1,2=1).
, где N и R1,2 коэффициенты,
значение которых определяются относительными параметрами плёнок (если плёнки
одинаковые, то N=R1,2=1).
Если плёнки одинаковые, то в (4) ![]() , а
, а ![]() . При d®¥ система (4) распадается на два несвязанных
нелинейных уравнения Шредингера (НУШ) с коэффициентами, соответствующими
несвязанным плёнкам 1 и 2, а при d=0 получим уравнение
с коэффициентами, соответствующими одиночной плёнке удвоенной толщины.
. При d®¥ система (4) распадается на два несвязанных
нелинейных уравнения Шредингера (НУШ) с коэффициентами, соответствующими
несвязанным плёнкам 1 и 2, а при d=0 получим уравнение
с коэффициентами, соответствующими одиночной плёнке удвоенной толщины.
Как показано в [13], решение системы уравнений типа (5) будет неустойчиво даже в том случае, если решение каждого из уравнений в отдельности устойчиво, т.е. ПМСВ являются модуляционно неустойчивыми в связанной структуре при возбуждении двух нормальных волн. Данный вид модуляционной неустойчивости, возникающей при одновременном распространении двух модуляционно устойчивых волн, связанных через нелинейность называется кросс-модуляцией [13].
В случае возбуждения одной из нормальных волн в структуре (![]() ) система уравнений (4) распадается
на два несвязанных нелинейных уравнения для каждой из нормальных волн и условие модуляционной неустойчивости в этом случае
имеет вид [2,4]:
) система уравнений (4) распадается
на два несвязанных нелинейных уравнения для каждой из нормальных волн и условие модуляционной неустойчивости в этом случае
имеет вид [2,4]:
Анализ коэффициентов в уравнениях (4) показал, что действие
связи не приводит к смене знаков коэффициентов нелинейности, а именно![]() <0 при любой величине связи. Однако,
возможно изменение знаков коэффициентов дисперсии
<0 при любой величине связи. Однако,
возможно изменение знаков коэффициентов дисперсии ![]() для одной из нормальных мод в узкой
области частот. Значение коэффициентов дисперсии
для одной из нормальных мод в узкой
области частот. Значение коэффициентов дисперсии ![]() рассчитывается
из дисперсионного соотношения (3).
рассчитывается
из дисперсионного соотношения (3).
(а)
(б)
(в)
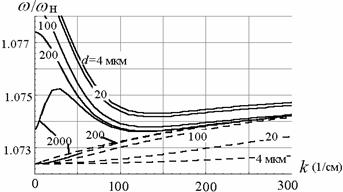
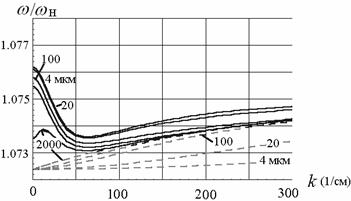
Рис. 2. Дисперсионные
характеристики ПМСВ для медленной волны (- - -), для быстрой волны (_____)
связанной структуры (при D1,2=20 мкм, ![]() =2630 Э, 4πM01,02=1750 Гс) (а) L®¥.
(б) L1,2 =100 мкм, (в) L1,2 =200 мкм.
=2630 Э, 4πM01,02=1750 Гс) (а) L®¥.
(б) L1,2 =100 мкм, (в) L1,2 =200 мкм.
Результаты решения дисперсионного уравнения (3) для различных значений связи (толщины диэлектрического промежутка между плёнками d) в отсутствии металлических экранов (L®¥.) представлены на рис. 2а. На этом же рисунке приведены дисперсионные кривые для одиночных плёнок железо-иттриевого граната (точечная кривая). Сплошные кривые соответствуют быстрым модам, а пунктирные – медленным модам связанной структуры.
Использование металлических экранов существенно влияет на дисперсию ПМСВ. На рис. 2б и 2в приведены кривые, рассчитанные с помощью дисперсионной зависимости, при фиксированном конечном значении L и различной величине связи d. Как следует из рисунков, металлические экраны сильно влияют на дисперсию одной верхней (быстрой) ветви МСВ и практически не влияют на другую нижнюю (медленную) дисперсионную ветвь. С приближением экранов при малых k на верхней ветви появляется участок аномальной дисперсии, тем больший, чем сильнее связь между плёнками (чем меньше d). Нижняя дисперсионная ветвь с приближением металла не деформируется. С дальнейшим уменьшением L аномальный участок на верхней кривой расширяется и при больших d на верхних ветвях появляется характерный перелом (см. рис. 2в). Важным обстоятельством является рост полосы пропускания с уменьшением L. Для малых L и достаточно малых d дисперсия верхней ветви во всей полосе становится аномальной, т.е. в связанной структуре в этом диапазоне частот возбуждается только обратная волна. В пределе при L®0 верхняя дисперсионная ветвь переходит в прямую. При достаточно больших L нижняя и верхняя ветви перекрываются практически во всей полосе пропускания, т.е. на каждой частоте существуют две волны с разными волновыми числами kб,м, быстрая и медленная. C уменьшением L, когда верхняя дисперсионная ветвь уходит в сторону более высоких частот, область перекрытия исчезает и появляется только для очень больших d. В этом случае в связанной системе на каждой частоте может возбуждаться только одна волна. При больших w она будет соответствовать нижней дисперсионной ветви (медленной МСВ моде), а при маленьких w – верхней (быстрой моде).
Как
видно из рис. 26,2в на заданной частоте w/wH в зависимости от величины связи (расстояния между
ферромагнитными плёнками d) и граничных условий (расстояния до металлических
экранов L) в структуре возможно распространение: одной нормальной моды
(быстрой или медленной), двух мод (быстрой и медленной, либо двух быстрых),
трёх мод (двух быстрых и медленной) или четырёх мод (трёх быстрых ![]() и одной медленной
и одной медленной ![]() ).
).
Рассмотрим
условия, при которых возможно возбуждение одной моды в структуре
![]() или
или![]() , соответственно . Для этого воспользуемся простой аналитической
теорией связанных волн [16]. Пусть имеются две линии передачи (в данной случае,
на МСВ), в которых могут распространяться несвязанные волны с постоянными
распространения k1 и k2 и амплитудами j1 и j2.
, соответственно . Для этого воспользуемся простой аналитической
теорией связанных волн [16]. Пусть имеются две линии передачи (в данной случае,
на МСВ), в которых могут распространяться несвязанные волны с постоянными
распространения k1 и k2 и амплитудами j1 и j2.
В отсутствии связи k1 и k2 положительны, фазовые и групповые скорости МСВ направлены в одну сторону. Если между волнами имеется связь, характеризующаяся коэффициентом связи K, то постоянные распространения изменяются, а амплитуды j1 и j2 становятся периодическими функциями продольной координаты. Полагая, что структура симметричная и плёнки одинаковые, т.е. k1=k2=k и примерное равенство скоростей несвязанных волн и K<<1 (т.е. слабую связь), уравнение связанных волн, описывающие линейную перекачку сигнала между плёнками запишем в виде:
где ![]() (i,j=1,2) определяются из соотношений (3) и зависят от
параметров структуры. Далее предположим, что j1 в случае связанных волн (для полного ВЧ поля) можно
записать как
(i,j=1,2) определяются из соотношений (3) и зависят от
параметров структуры. Далее предположим, что j1 в случае связанных волн (для полного ВЧ поля) можно
записать как
Исходя
из последних соотношений (6) и (7) можно получить выражение для
![]() . C учётом начальных условий, налагаемых на начальные
амплитуды
. C учётом начальных условий, налагаемых на начальные
амплитуды ![]() волн в линиях и их производные, можно прийти к
следующему соотношению, определяющему условия возбуждения каждой из нормальных
волн в с
волн в линиях и их производные, можно прийти к
следующему соотношению, определяющему условия возбуждения каждой из нормальных
волн в с ![]() или
k, соответственно, в отдельности:
или
k, соответственно, в отдельности:
Значения
волновых чисел ![]() и K известны из решения соответствующих дисперсионных
уравнений для связанных и одиночных структур (3). В случае, если в структуре
возбуждаются две моды, условия (8) переходят в простые соотношении,
соответствующие возбуждению каждой из нормальных волн, быстрой или медленной, в
отдельности:
и K известны из решения соответствующих дисперсионных
уравнений для связанных и одиночных структур (3). В случае, если в структуре
возбуждаются две моды, условия (8) переходят в простые соотношении,
соответствующие возбуждению каждой из нормальных волн, быстрой или медленной, в
отдельности:
Как отмечалось ранее, при возбуждении одной моды в структуре магнитостатическая волна является неустойчивой при выполнении условия (5). Так как при изменении L и d возможно изменение знаков коэффициента дисперсии нормальных волн, то можно предположить, что в связанной металлизированной структуре в определённо области частот возможна модуляционная неустойчивость ПМСВ при возбуждении одной моды. Для определения этих областей проводился расчёт коэффициентов Aб,м и Bбб,мм, и рассчитывались значения частот для которых значения этих коэффициентов удовлетворяют условия (5).
|
L/D=¥ (а) L/D =2 (б) L/D=0.7
(в) |
L/D=0.5
(г) L/D=0.2
(д) L/D=0.01
(е) |
|
|
|
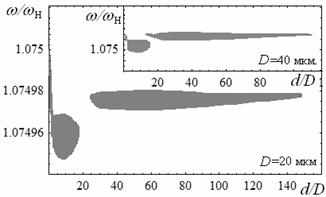
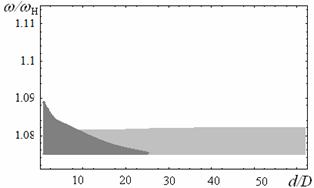
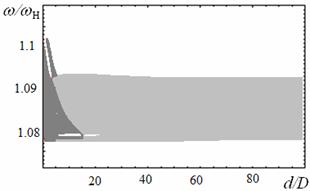
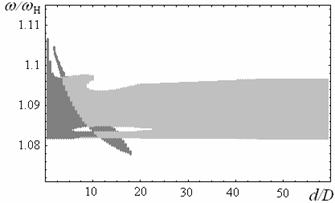
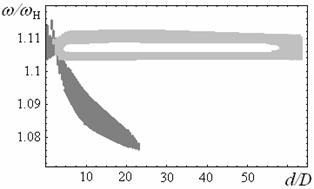
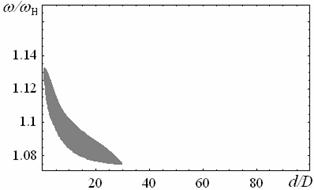
На рисунках 3а-е показаны плоскости параметров, демонстрирующие области модуляционной неустойчивости при возбуждении только быстрой волны в рассматриваемой структуре металл-ферромагнетик-диэлектрик-ферромагнетик-металл. Рассчитаны области изменения параметров с учетом расстояния от ферромагнитных плёнок до металлических экранов L1,2, демонстрирующие возможность модуляционной неустойчивости в системе при возбуждении быстрой волны. Для медленной моды диапазон частот, соответствующий неустойчивости практически не изменяется при приближении металлических экранов, т.к. граничные условия слабо влияют на дисперсию медленной поды (см. рис. 2б). При возбуждении нескольких мод в структуре, как отмечалось ранее, ПМСВ является неустойчивой при любой величине связи из-за наличия кросс-модуляции.
Как
видно из рис. 3а в свободной связанной структуре в отсутствие металлических экранов
(L/t®¥) имеет место очень узкая область частот, соответствующая модуляционной
неустойчивости ПМСВ (при уменьшении толщин плёнок область изменения параметра d,
при котором возможна неустойчивость, сужается (см. вставку к рис.3а). По мере
приближения экранов (с уменьшением L) область частот,
соответствующая неустойчивости ПМСВ значительно расширяется, сдвигается в
сторону более высоких частот и расщепляется на две, как показано на рис.
3б-д.
Различным цветом на рис. 3б-д показаны области неустойчивости, которые
возникают при различных способах возбуждения: возбуждение только ![]() (темный цвет) или
(темный цвет) или ![]() (светлый
цвет). Видно, что приближение металлических экранов приводит к существенной
деформации областей параметров, соответствующих модуляционной неустойчивости,
как показано на рис. 3.
(светлый
цвет). Видно, что приближение металлических экранов приводит к существенной
деформации областей параметров, соответствующих модуляционной неустойчивости,
как показано на рис. 3.
Видно,
что при d®¥ при
конечных значениях L и
возбуждении ![]() всегда имеется область частот, соответствующая
модуляционной неустойчивости, что соответствует существованию области с
положительной дисперсией на дисперсионной характеристике волн в связанной
структуре с металлом (см., например, рис. 2б). При d=0 (что
соответствует плёнке удвоенной толщины), в отсутствии металла ПМСВ, как
отмечалось выше и показано на рис. 3а, является устойчивой. В металлизированной
с обоих сторон одиночной плёнке удвоенной толщины (рис. 3б-д) (при d=0)
существуют частоты, при которых ПМСВ не устойчива. При L®0 диапазон частот,
соответствующий неустойчивости является максимальным.
всегда имеется область частот, соответствующая
модуляционной неустойчивости, что соответствует существованию области с
положительной дисперсией на дисперсионной характеристике волн в связанной
структуре с металлом (см., например, рис. 2б). При d=0 (что
соответствует плёнке удвоенной толщины), в отсутствии металла ПМСВ, как
отмечалось выше и показано на рис. 3а, является устойчивой. В металлизированной
с обоих сторон одиночной плёнке удвоенной толщины (рис. 3б-д) (при d=0)
существуют частоты, при которых ПМСВ не устойчива. При L®0 диапазон частот,
соответствующий неустойчивости является максимальным.
Таким образом, в работе показано, что при распространении нелинейных поверхностных МСВ в слоистых ферромагнитных структурах типа возможна модуляционная неустойчивость этого типа волн при определенных параметрах структур. Использование металлических экранов в таких структурах даёт возможность эффективно управлять размером и местоположением областей модуляционной неустойчивости за счёт изменения расстояния между плёнками и способа возбуждения структуры.
Работа выполнена в рамках Программы Федерального агентства по образованию и CRDF «Развитие научного потенциала высшей школы на 2006-2007 гг.» (Appendix–06-04) и при поддержке РФФИ (гранты № 07-02-00639 и № 05-02-16273).
Список литературы
[1] Лукомский В.П.// Укр. физ. журн. 1978. т.23, № 1. c.134.
[2] Звездин А.К., Попов А.Ф.// ЖЭТФ. 1983. т.84, вып.2. с.606-615.
[3] Boardman A. D., Wang Q., Nikitov S.A.// IEEE Trans. in Mag. 1994. v.30, №1. p.14.
[4] Вашковский А.В., Стальмахов В.С., Шараевский Ю.П. Магнитостатические волны в электронике сверхвысоких частот. Саратов: СГУ. 1993. 320с.
[5] Киндяк А.С.// ЖТФ. 1999. т.69, вып. 6. с.119.
[6] Киндяк А.С.// Письма в ЖТФ. 1999. т.25, вып.4. с.48-54.
[7] Короткевич А.О, Никитов С.А.// ЖЭТФ. 1999. т.116, вып.6(12). с.205.
[8] Кокин А.В., Никитов С.А.// ФТТ. 2001. т.43, вып.5. с.851.
[9] Малюгина М.А., Шараевский Ю.П.// Изв.ВУЗов–Прикладная нелинейная динамика. 2000. т.8, №3. c.59-69.
[10] Дудко Г.М., Малюгина М.А., Шараевский Ю.П.// Изв.ВУЗов–Прикладная нелинейная динамика. 2003. т.8, №6.
[11] Boardman A.D., Xie K.// Phys. Rev. Lett. 1995. v.75, №25. p.4591.
[12] Marcelli R., Nikitov S.A.// Europhys. Lett. 2001. v.54, №1. p.91-97.
[13] Agrawal G.P.// Phys. Rev. A. 1989. v.39, №7. p.3406-3413.
[15].
Агравал Г. Нелинейная волоконная оптика. М.:Мир. 1996.
[16]. Люиселл У. Связанные и параметрические колебания в электронике. М.:ИЛ.
1963.

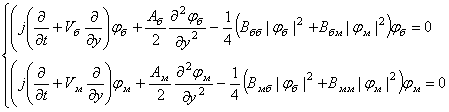 , (4)
, (4)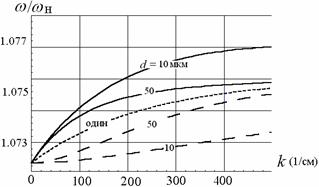
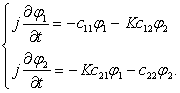 (6)
(6)