Анализ протоколов шифрования
В. Н. Никитин, Д. В. Юркин
Санкт-Петербургский Государственный университет телекоммуникаций
им. проф. М.А. Бонч-Бруевича
Получена 1 апреля 2009 г.
Выбор приоритетного алгоритма шифрования
для защищенной системы передачи данных, работающей по реальным каналам связи с
ошибками, не дает возможность оптимального повышения ее пропускной способности.
Поэтому встает вопрос о том, какой протокол шифрования обеспечит максимальную
эффективность использования пропускной способности открытого канала связи и
обеспечит наивысшее качество связи. В данной
работе были исследованы различные схемы организации каналов передачи данных с
переспросом, защищенных криптографическими методами, что позволило оценить
изменение пропускной способности защищенного канала по отношению к открытому.
Также оценивается зависимость пропускной способности защищенного канала от
соотношения скоростей работы шифратора и передачи данных по открытому каналу и
организации приемо-передающего тракта.
Ключевые слова:
защита информации,
передача данных, шифрование.
Описание структуры канала при передаче данных с использованием механизмов различных алгоритмов шифрования
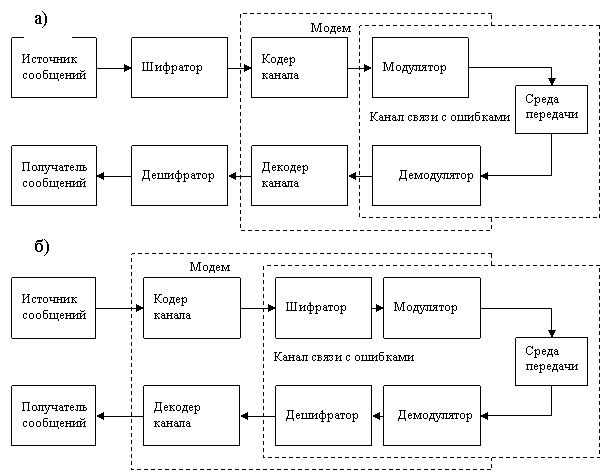
Анализируя структуру канала передачи данных можно установить, что узлы шифрования (дешифрования) данных как показано на рисунке 1 могут включаться либо (Рис. 1а) как автономные устройства тракта между источником (получателем) сообщений и модемом, либо (Рис. 1б) как составные элементы модемов, включаемые между кодером (декодером) и модулятором (демодулятором). При этом для шифрования данных могут использоваться как блоковые, так и потоковые алгоритмы.
Рис. 1. Структуры тракта передачи
данных с узлами шифрования (дешифрования) данных.
Рассмотрим особенности использования данных алгоритмов в протоколах передачи данных.
При
автономном использовании шифраторов (Рис. 1а), исходное сообщение разбивается
на блоки длиной ![]() символов,
над каждым из которых выполняется блоковое шифрование. В зависимости от
выбранного алгоритма шифрования блоки криптограммы могут иметь ту же длину
символов,
над каждым из которых выполняется блоковое шифрование. В зависимости от
выбранного алгоритма шифрования блоки криптограммы могут иметь ту же длину ![]() , что и на входе, либо
длину
, что и на входе, либо
длину ![]() . Полученные блоки криптограммы
конкатенируются и поступают в канальный кодер модема, где осуществляется
помехоустойчивое кодирование зашифрованного сообщения. В дальнейшем будем
предполагать, что повышение достоверности передачи обеспечивается применением
алгоритма решающей обратной связи с адресным переспросом. Для этого поступающее
зашифрованное сообщение разбивается на новые блоки длины
. Полученные блоки криптограммы
конкатенируются и поступают в канальный кодер модема, где осуществляется
помехоустойчивое кодирование зашифрованного сообщения. В дальнейшем будем
предполагать, что повышение достоверности передачи обеспечивается применением
алгоритма решающей обратной связи с адресным переспросом. Для этого поступающее
зашифрованное сообщение разбивается на новые блоки длины ![]() . Далее блоки данных кодируются кодом заданным
. Далее блоки данных кодируются кодом заданным ![]() - кодом [3]. Полученные кодовые слова выводятся на вход
модулятора, сигнальные конструкции которого передаются по каналу связи.
- кодом [3]. Полученные кодовые слова выводятся на вход
модулятора, сигнальные конструкции которого передаются по каналу связи.
При
установке шифратора между канальным кодером и модулятором (Рис. 1б) сообщения с
выхода источника разбиваются на блоки длины ![]() , кодируются
, кодируются ![]() - кодом,
конкатенируются и повторно разбиваются на блоки длины
- кодом,
конкатенируются и повторно разбиваются на блоки длины ![]() для выполнения шифрования, в результате которого формируются блоки
для выполнения шифрования, в результате которого формируются блоки ![]() , которые конкатенируются и поступают на вход модулятора аналогично
первой схеме с передачей по каналу связи.
, которые конкатенируются и поступают на вход модулятора аналогично
первой схеме с передачей по каналу связи.
На приемной стороне после детектирования сообщения в первом случае выполняется канальное декодирование и декодирование источника сообщения с последующим дешифрованием. Во втором случае дешифрование выполняется перед канальным декодированием.
При
использовании потоковых алгоритмов шифрование сообщения осуществляется посимвольно,
без внесения избыточности [9]. Однако с целью защиты от накопления статистики
[11] осуществляется динамическая смена вектора инициализации (![]() ) алгоритма потокового шифрования. С этой целью после передачи каждых
) алгоритма потокового шифрования. С этой целью после передачи каждых ![]() бит информации от
источника происходит передача служебного сообщения, содержащего
бит информации от
источника происходит передача служебного сообщения, содержащего![]() длинной
длинной ![]() бит.
бит.
В первом
случае (Рис. 1а), исходное сообщение обрабатывается потоковым [12] шифратором.
Затем зашифрованное сообщение разбивается на блоки длины ![]() , которые кодируются
помехоустойчивым
, которые кодируются
помехоустойчивым ![]() -
кодом. Полученные в результате блоки длины
-
кодом. Полученные в результате блоки длины ![]() объединяются в поток и выводятся на вход модулятора, сигнальные конструкции
которого передаются по каналу связи.
объединяются в поток и выводятся на вход модулятора, сигнальные конструкции
которого передаются по каналу связи.
Во втором случае (Рис. 1б), исходное сообщение сначала кодируется помехоустойчивым кодом, после чего шифруется и передается по каналу, аналогично первой схеме.
Анализ протоколов передачи данных с использованием блокового шифрования
Известно, что при декодировании сообщения декодером максимального правдоподобия, оценка нижней границы вероятности обнаруженной битовой ошибки определена величиной [4,7]:
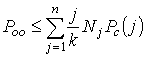
Где ![]() - число кодовых слов веса
- число кодовых слов веса ![]() , а
, а ![]() определено как:
определено как:
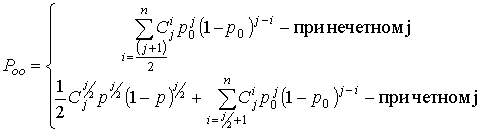
Где ![]() - вероятность битовой ошибки на входе
декодера.
- вероятность битовой ошибки на входе
декодера.
Например,
для кодов Хэмминга [3] известно распределения весов кодовых слов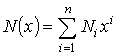 , при
, при ![]() и
и ![]() :
:
![]()
Известно
также, что при использовании блоковых шифров ошибки в криптограмме, порожденные
каналом связи размножаются при дешифровании. Таким образом, вероятность битовой
ошибки на выходе дешифратора [6] равна ![]() , где
, где ![]() , это коэффициент
размножения ошибок шифратором за одну итерацию подстановки, а
, это коэффициент
размножения ошибок шифратором за одну итерацию подстановки, а ![]() , это число итераций
подстановки.
, это число итераций
подстановки.
Остановимся на первой схеме с размещением шифратора до канального кодера. В ней, как и во второй осуществляется декодирование в ближайшее кодовое слово по максимуму правдоподобия (для ДСК они совпадают, поскольку метрика Хэмминга согласована с двоичным симметричным каналом).
Закодированные
криптограммы длины ![]() символов
передаются, конкатенируясь друг за другом в последовательность длины
символов
передаются, конкатенируясь друг за другом в последовательность длины ![]() . В случае обнаружения
ошибки по обратному каналу передается информационное сообщение об обнаруженных
искажениях. После чего на передающей стороне выполняется повторная передача
кодового слова, содержащего обнаруженную ошибку.
. В случае обнаружения
ошибки по обратному каналу передается информационное сообщение об обнаруженных
искажениях. После чего на передающей стороне выполняется повторная передача
кодового слова, содержащего обнаруженную ошибку.
Таким образом, достоверный прием блока сообщения будет случайным событием, а процесс доставки каждого блока сообщения можно описать вероятностным графом [1].
Вероятностный граф передачи одного блока сообщения будет иметь вид:
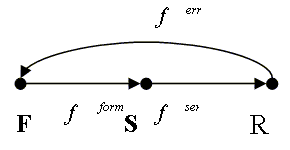
|
|
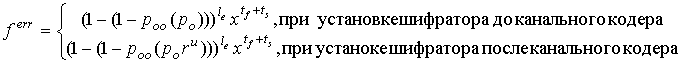
![]()

Множитель
![]() определяет
величину коэффициента размножения ошибок шифратором. Параметры
определяет
величину коэффициента размножения ошибок шифратором. Параметры ![]() ,
,![]() ,
,![]() определяют время передачи, формирования сообщения
и длину криптограммы соответственно.
определяют время передачи, формирования сообщения
и длину криптограммы соответственно.
В общем
случае, при передаче ![]() блоков сообщения в обоих вариантах установки блокового шифратора вероятностный граф
протокола передачи выглядит следующим образом.
блоков сообщения в обоих вариантах установки блокового шифратора вероятностный граф
протокола передачи выглядит следующим образом.

Рис.
2. Вероятностный граф протокола передачи сообщений с использованием блокового
шифра.
Определим
характер функциональной зависимости среднего времени выполнения протокола от
величины битовой ошибки в ДСК. Она определяется как производная от
производящей функции по переменной ![]() в точке начальной
вершины графа [8].
в точке начальной
вершины графа [8].
Применение теории вероятностных графов позволит получить такие характеристики процесса передачи сообщений в анализируемых схемах как зависимости среднего времени передачи одного блока и средней скорости передачи сообщения от вероятности битовой ошибки в канале связи [1].
Поскольку
производящая функция передачи одного блока сообщения будет иметь вид 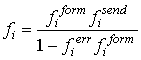 , а производящая
функция передачи всех блоков сообщения будет
, а производящая
функция передачи всех блоков сообщения будет 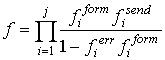 .
.
Вычисление
производной по переменной ![]() в точке
в точке ![]() от производящей функции передачи одного
блока криптограммы
от производящей функции передачи одного
блока криптограммы
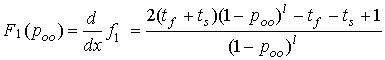
позволяет получить зависимость среднего времени передачи одного блока сообщения от вероятности битовой ошибки в канале связи
![]()
Разделим
типологически алгоритм передачи одного сообщения с переспросом. Для этого вынесем
из общей группы конструкций формирования сообщения ту, в которой реализована
процедура шифрования исходного открытого текста, формирование сообщения и
подготовку к отправке. Эта процедура имеет трудоемкость ![]() (где
(где ![]() это трудоемкость выполнения элементарной
операции) и описывается производящей функцией
это трудоемкость выполнения элементарной
операции) и описывается производящей функцией ![]() .
Оставшуюся группу конструкций, отвечающую за передачу сообщения, объединим в цикл
и граничным условием для перехода в начало по флагу, возвращаемому функцией
.
Оставшуюся группу конструкций, отвечающую за передачу сообщения, объединим в цикл
и граничным условием для перехода в начало по флагу, возвращаемому функцией ![]() с вероятностями
с вероятностями ![]() для первого случая или
для первого случая или
![]() для второго.
Определим вероятностный граф полученного алгоритма выполнения протокола
шифрования.
для второго.
Определим вероятностный граф полученного алгоритма выполнения протокола
шифрования.
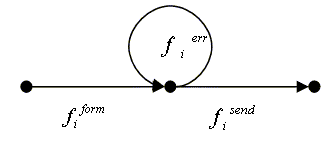
Рис. 3. Вероятностный граф
протокола блокового шифрования с разделенной топологией.
Производящая функция
данного алгоритма будет иметь вид: 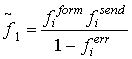
Вычислим
производную по переменной ![]() в точке
в точке ![]() от производящей функции передачи одного
блока криптограммы:
от производящей функции передачи одного
блока криптограммы:
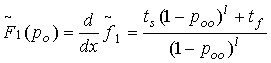
Затем
вычислим производную для ![]() последовательно передаваемых сообщений
последовательно передаваемых сообщений ![]() , она будет определена
как
, она будет определена
как
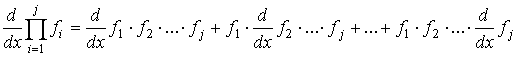 .
.
Таким
образом в данной зависимости присутствуют производящие функции, их производные
первого порядка и линейные комбинации из их произведений. Исследуя эту функцию
на монотонность, можно показать, что 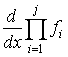 монотонно возрастает, если монотонно
возрастает
монотонно возрастает, если монотонно
возрастает ![]() и
ее первая производная
и
ее первая производная ![]() ,
для чего достаточным условием будет
,
для чего достаточным условием будет 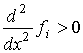 . Основываясь на вышесказанном, может утверждать,
что вероятностно-временные характеристики протокола передачи являются монотонно
возрастающими во всей области определения.
. Основываясь на вышесказанном, может утверждать,
что вероятностно-временные характеристики протокола передачи являются монотонно
возрастающими во всей области определения.
Особенности передачи данных с использованием потокового шифрования
Так как
введение потокового шифратора в систему передачи данных не приводит к
размножению ошибок на приемной стороне, то функциональные зависимости,
определяющие производящие функции переходов в различные состояния протокола
будут соответствовать функциям для случая установки шифратора до канального
кодера и коэффициент размножения ошибок будет равен единице. Основным отличием применения
данного протокола шифрования является необходимость передачи данных (векторов
инициализации), синхронизирующих работу шифраторов обоих корреспондентов. Как
было отмечено выше, периодическая передача векторов инициализации обусловлена
необходимостью защиты потокового шифратора от сбоев синхронизации работы
шифратора и дешифратора и от накопления статики. Однако ошибки, возникшие в
канале связи при передаче вектора инициализации, будут приводить к ошибкам
синхронизации шифратором передачи и приема и, как следствие, к возникновению
ошибочных блоков сообщений длиной ![]() бит. При установке дешифратора после декодера канала
(Рис. 1а) ошибочно расшифрованные блоки будут поступать получатель, что
недопустимо. Однако такие ошибки легко обнаруживаются при установке дешифратора
перед декодером канала (Рис. 1б) и блокируются. Неправильно принятые сообщения
в таком случае будут переданы повторно. Определим вероятностный граф протокола:
бит. При установке дешифратора после декодера канала
(Рис. 1а) ошибочно расшифрованные блоки будут поступать получатель, что
недопустимо. Однако такие ошибки легко обнаруживаются при установке дешифратора
перед декодером канала (Рис. 1б) и блокируются. Неправильно принятые сообщения
в таком случае будут переданы повторно. Определим вероятностный граф протокола:

Рис. 4. Вероятностный граф протокола потокового шифрования.
Производящие функции будут иметь следующий вид:
![]()
![]()
![]()
![]()
![]()
Далее разделим
типологически алгоритм общей конструкции передачи одного фрагмента данных между
передачами вектора инициализации потокового шифратора на три последовательно
выполняемые конструкции: формирование передача IV, формирование
сообщения, передача сообщения. Таким образом, конструкции передачи вектора
инициализации и блока информационного сообщения независимы, т.е. ![]() и
и
![]() .
.
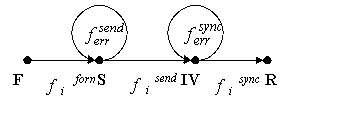
Рис. 5. Вероятностный граф
протокола потокового шифрования с разделенной топологией.
Производящая функция
данного алгоритма будет иметь вид: 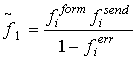
Вычислим
производную по переменной ![]() в точке
в точке ![]() от производящей функции передачи одного
блока криптограммы аналогично вышеприведенным расчетам.
от производящей функции передачи одного
блока криптограммы аналогично вышеприведенным расчетам.
Сравнительный анализ ВСХ протоколов блокового шифрования
Построим графики функций относительной
скорости выполнения протокола ![]() и
и ![]() , [1] исходя из условий:
, [1] исходя из условий:
1) Канал двоичный симметричный, скорость канала “вверх” равна скорости канала “вниз”.
2) Пропускная способность канала связи составляет 1 Мбит/с, 10 Мбит/с, 100 Мбит/с.
3) Блок данных состоит трех сообщений длиной 64 бита.
4)
Время формирования одного сообщения ![]() с.
с.
Определим как среднюю относительную скорость функцию ![]() равную, обратной
величине среднего времени выполнения протокола
равную, обратной
величине среднего времени выполнения протокола ![]() умноженной на частное от длины
криптограммы
умноженной на частное от длины
криптограммы ![]() и
битовой
и
битовой ![]() пропускной
способности канала.
пропускной
способности канала.
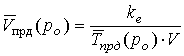
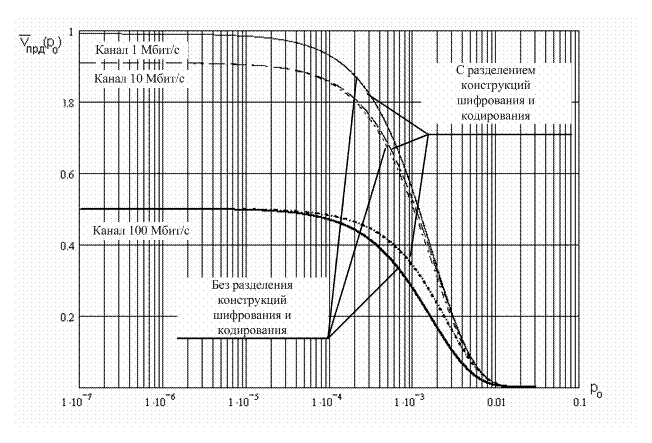
Рис. 6. Средняя скорость передачи блоков криптограммы с ошибками в
системе с переспросом, при различных топологиях вероятностного графа.
На котором жирными сплошной и пунктирной с точкой кривой показано относительное снижение скорости выполнения алгоритма с неразделенной и разделенной топологиями соответственно в канале 100 Мбит/с. Далее пунктирной и пунктирной с точкой линиями показаны аналогичные кривые для скорости 10 Мбит/с. И в сплошную линию слились в данном масштабе кривые для 1 Мбит/с.
Рассмотрим схему
с установкой шифратора после канального кодера. Предположим, что СПДС работает
при вышеуказанных условиях и что шифратор имеет в своей структуре 32 раунда
подстановки с коэффициентом размножения ошибки 1,2 на каждом раунде.
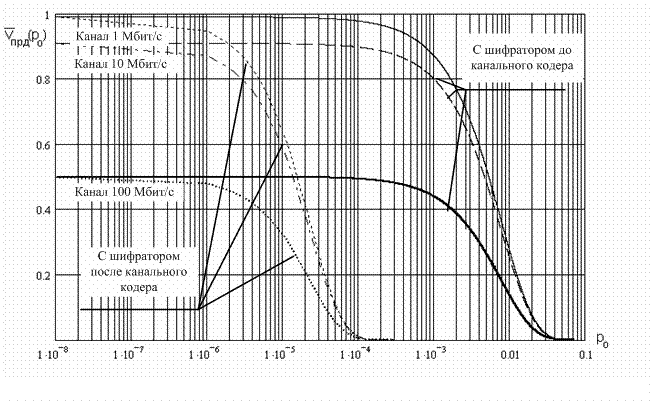
Рис. 7. Средняя скорость передачи блоков криптограммы с ошибками в системе с переспросом, в различных схемах установки блокового шифратора.
Как видно по
графикам зависимости среднего снижения скорости канала от вероятности битовой
ошибки в канале связи ![]() (рис
7.), наилучшими ВСХ обладают протоколы с разделенной топологией и шифратором
(рис.) расположенным до канального кодера.
(рис
7.), наилучшими ВСХ обладают протоколы с разделенной топологией и шифратором
(рис.) расположенным до канального кодера.
Однако следует
заметить, что в канале без ошибки (![]() ) время передачи в обоих случаях будет
одинаково. Этот факт дает основание утверждать, что подобное разделение
конструкций формирования и передачи сообщения адаптирует алгоритм протокола к
каналу связи с ошибками.
) время передачи в обоих случаях будет
одинаково. Этот факт дает основание утверждать, что подобное разделение
конструкций формирования и передачи сообщения адаптирует алгоритм протокола к
каналу связи с ошибками.
Исходя из полученных результатов,
представим граф протокола шифрования ![]() блоков сообщения (рис.8).
блоков сообщения (рис.8).

Рис 8.
Вероятностный граф протокола передачи ![]() блоков криптограммы с разделенной
топологией.
блоков криптограммы с разделенной
топологией.
При передаче сообщении по каналу организованному с шифратором расположенном после кодера на передающей стороне (и перед декодером на приемной) ВСХ получаются на несколько порядков хуже чем с шифратором до кодера канала. И аналогично с топологией протокола это наблюдается только в каналах плохого качества а, к примеру, при нулевой вероятности ошибки время передачи сообщения одинаково в обоих случаях.
Таким образом, можно сказать, что алгоритм протокола блокового шифрования, соответствующий графу рис. с шифратором, размещенным по верхней схеме рис. имеет наилучшие ВСХ в канале с ошибками.
Сравнительный анализ ВСХ протоколов потокового шифрования
Построим графики функций
относительной скорости выполнения протокола, аналогично вышеприведенным
расчетам ![]() и
и
![]() , [1] исходя
из условий:
, [1] исходя
из условий:
5) Канал двоичный симметричный, скорость канала “вверх” равна скорости канала “вниз”.
6) Пропускная способность канала связи составляет 1 Мбит/с, 10 Мбит/с, 100 Мбит/с.
7) Длина блока данных состоит из двух сообщений: вектора инициализации длиной 40 бит и сообщения длинной 256 бит.
8)
Время формирования одного бита сообщения ![]() с.
с.
Приведем сравнительные
характеристики протоколов.
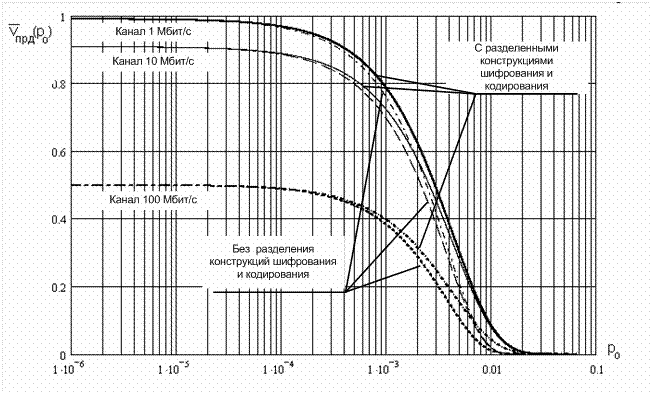
Рис. 9. Относительная средняя скорость передачи блоков криптограммы в системе с переспросом при установке потокового шифратора с различной топологией вероятностного графа.
Как видно по графикам средней скорости канала, ситуация аналогична протоколу блокового шифрования: алгоритм с разделенной структурой графа имеет лучшие ВСХ чем с неразделенной, также среднее время передачи при нулевой вероятности у обоих одинаково. Поэтому вероятностный граф адаптированного протокола выглядит следующим образом рис.10

Рис 10. Вероятностный
граф протокола передачи ![]() блоков криптограммы с разделенной
топологией.
блоков криптограммы с разделенной
топологией.
Улучшение ВСХ
большей частью связано с тем, что вероятность успешной передачи вектора
инициализации равна ![]() ,
что приводит к значительному увеличению среднего времени передачи последующей
за ним криптограммы в едином цикле передачи. Вынесение конструкции формирования
и передачи
,
что приводит к значительному увеличению среднего времени передачи последующей
за ним криптограммы в едином цикле передачи. Вынесение конструкции формирования
и передачи ![]() , а
также формирования сообщения позволяет ощутимо повысить скорость передачи
сообщений.
, а
также формирования сообщения позволяет ощутимо повысить скорость передачи
сообщений.
Выводы
В данной работе были исследованы различные схемы организации каналов передачи данных с переспросом и применением симметричных шифров.
Результаты оценки пропускной способности защищенного канала по отношению к открытому показывают, что применение криптографических алгоритмов шифрования данных влияет на пропускную способность системы передачи данных. На основании этих результатов можно сформулировать следующие выводы.
Вне зависимости от качества канала связи пропускная способность защищенного канала зависит от соотношения скоростей работы шифратора и передачи данных по открытому каналу.
При снижении качества канала связи, пропускная способность защищенного канала передачи данных уменьшается по сравнению с открытым и зависит как от выбранного протокола шифрования, так и от места установки шифраторов в тракте передачи.
Разделение конструкций формирования и передачи блока сообщения дает преимущественное улучшение пропускной способности канала при скорости формирования сообщения меньшей или равной скорости его передачи в каналах плохого качества. Также такое разделение не снижает пропускную способность хороших каналов с низкой вероятностью ошибки.
Установка блокового шифратора в модеме приводит к существенному снижению
пропускной способности канала связи, по причине размножения шифром канальных
ошибок. В этом случае эффективность канального кодера с заданным ![]() кодом падает, что приводит к
снижению пропускной способности. Этого можно избежать, реализовав функцию
шифрования непосредственно в источнике сообщения или сразу после него.
кодом падает, что приводит к
снижению пропускной способности. Этого можно избежать, реализовав функцию
шифрования непосредственно в источнике сообщения или сразу после него.
При применении потокового шифра эффективность использования пропускной способности канала не зависит от места шифраторов в тракте передачи, так как канальных ошибок он не размножает. Но такой шифр чувствителен к синхронизации работы шифраторов передачи и приема. Передачи вектора инициализации шифраторов снижает пропускную способность защищенного канала. Для уменьшения этого влияния конструкция, в которой передается вектор инициализации, должна быть выделена из общего цикла передачи сообщения и в ней реализован механизм проверки ошибок с переспросом.
Для выбора приоритетного алгоритма шифрования для канала связи с ошибками требуется более детальный анализ с подробным рассмотрением частных случаев.
Список литературы
1) Г. А. Емельянов, В. О. Шварцман, Передача дискретной информации: [Учебник для электротехн. ин-тов связи] / М. Радио и связь 1982
2) С. Мэзон, Г. Циммерман. Электронные цепи, сигналы и системы. "Издательство иностранной Литературы", 1963.
3) Соловьева Ф.И. Введение в теорию кодирования: Учебное пособие / Новосибирский государственный университет, Новосибирск, 2006.
4) Золотарев В.В., Овечкин Г.В. Помехоустойчивое кодирование. Методы и алгоритмы: справочник / Под ред. Чл.-кор. РАН Ю.Б. Зубарева. – М: Горячая линия – Телеком, 2004.
5) F. Chabaud, On the security of some cryptosystems based on error-correcting codes, Advances in Cryptology–EUROCRYPT ’94, 1995
6) H. Faestal, Cryptography and computer privacy. Scientific American, 1973.
7) T. Johansson, G. Kabatinskii, B. Smeets, “On the relation between Acodes and codes correcting independent errors”, Advances in Cryptology–EUROCRYPT’93 1994.
8) O. Ore, Graphs and their uses. Random house, New York, 1963.
9) RSA Laboratories, Stream ciphers, Technical Report TR-701, 1995.
10) S. Lin, D. Costello, Error Control Coding: Fundamentals and Applications, Prentice Hall, Englewood Cliffs, New Jersey,1983
11) New approaches to the design of selfsynchronizing stream ciphers, Advances in Cryptology–EUROCRYPT ’91,1991
12) N. Proctor, A self-synchronizing cascaded cipher system with dynamic control of error propagation, Advances in Cryptology– Proceedings of CRYPTO 84, 1985.