УДК 517.5: 535+537.8: 621.37
ТЕОРЕТИЧЕСКОЕ ИССЛЕДОВАНИЕ КОРРЕКТНОСТИ ОБРАТНОЙ ЗАДАЧИ ВОЛНОВОДНОГО РАССЕЯНИЯ ЛАЗЕРНОГО ИЗЛУЧЕНИЯ В СТАТИСТИЧЕСКИ НЕРЕГУЛЯРНОМ ИНТЕГРАЛЬНО-ОПТИЧЕСКОМ ВОЛНОВОДЕ В ОТСУТСТВИЕ ШУМА
А. А. Егоров
Институт общей физики им. А.М. Прохорова РАН
Получена 10 апреля 2009 г.
Исследована корректность линейной обратной задачи теории рассеяния лазерного излучения в статистически нерегулярном интегрально-оптическом волноводе в отсутствие шума. Доказано, что при вполне естественных физических и математических ограничениях, наложенных на диаграмму рассеяния, можно получить приближенное корректное решение поставленной обратной задачи волноводного рассеяния лазерного излучения в виде ряда Тейлора. Единственность полученного решения обратной задачи основана на свойствах аналитических функций. Устойчивость решения к малым изменениям входных данных обеспечена сужением возможного класса решений до некоторого компактного множества.
Ключевые слова: интегральная оптика, лазерное излучение, обратная задача рассеяния, статистические нерегулярности, автокорреляционная функция, некорректные задачи, обработка данных.
1. ВВЕДЕНИЕ
Интенсивное развитие интегральной оптики и волноводной оптоэлектроники за последние 30-40 лет значительно продвинуло исследование процессов распространения и преобразования электромагнитного излучения, как в регулярных, так и в нерегулярных интегрально-оптических волноводах [1-16].
Перспективы развития интегральной оптики и волноводной оптоэлектроники в последние годы, несомненно, связаны с применением новых высокоточных оптических методов исследования и контроля объектов с субмикронной топологией. Особенно эта проблема актуальна в области интегрально-оптических нанотехнологий. По нашему мнению использование явления волноводного рассеяния лазерного излучения [1-7, 13-22] для метрологического контроля в интегральной оптике и волноводной оптоэлектронике является наиболее адекватным решением вышеуказанных проблем.
Важно отметить, что в большинстве публикаций по волноводному рассеянию лазерного излучения практически отсутствует постановка обратной задачи рассеяния и обсуждение связанной с ней проблемы корректности, особенно при изменении радиуса корреляции нерегулярностей в широком диапазоне значений, включая длину волны падающего излучения. Более того, обратная задача волноводного рассеяния, как в отсутствие, так и при наличии шума до сих пор не была решена. Поэтому ее решение – это актуальная задача теории волноводного рассеяния.
В работах [17-19, 21, 22] последовательно развит новый метод решения обратной задачи волноводного рассеяния лазерного излучения в нерегулярном интегрально-оптическом волноводе. Метод заключается в регистрации диаграммы рассеяния точечным фотоприемником в дальней (или в эквивалентной ей плоскости Фурье [17]), ближней или промежуточной зоне и последующей обработке оцифрованных значений интенсивности рассеянного в волноводе излучения. В результате можно найти приближенное корректное решение обратной задачи: восстановить автокорреляционную функцию и/или функцию спектральной плотности статистических нерегулярностей и определить соответствующие параметры нерегулярностей.
В настоящей работе теоретически исследуется проблема корректности обратной задачи волноводного рассеяния лазерного излучения на статистических нерегулярностях интегрально-оптического трехслойного двухмерного волновода при не зашумленных входных данных, полученных в дальней зоне или в некоторой эквивалентной ей плоскости Фурье.
2. ОБРАТНАЯ ЛИНЕЙНАЯ ЗАДАЧА ТЕОРИИ ВОЛНОВОДНОГО РАССЕЯНИЯ
В математической физике различают корректно поставленные и некорректно поставленные задачи [23-25]. Задача называется корректно поставленной, если выполняются следующие требования: 1) ее решение существует, 2) это решение определяется однозначно и 3) решение непрерывно зависит от входных данных, т.е. малым изменениям входных данных соответствуют малые изменения в решении задачи. Последнее требование называется свойством устойчивости решения задачи. Задачи, не удовлетворяющие данным требованиям, называются некорректно поставленными.
Обратные задачи теории рассеяния света входят в общий класс некорректно поставленных задач математической физики [24]. Действительно, в этом случае об исследуемом объекте судят по данным измерений рассеянного излучения, несущего информацию об оптико-физических свойствах объекта [1-23].
Анализ двухмерной задачи волноводного рассеяния лазерного излучения [1-4, 13-19]
показывает: а) решение обратной задачи в виде ![]() может не существовать, например,
если
может не существовать, например,
если ![]() не
существует (не выполняется первое требование корректности); б) даже если такое
решение задачи
не
существует (не выполняется первое требование корректности); б) даже если такое
решение задачи ![]() существует,
оно может не обладать свойством устойчивости, поскольку зачастую оператор
существует,
оно может не обладать свойством устойчивости, поскольку зачастую оператор ![]() не является непрерывным
(не выполняется третье требование корректности). Таким образом, поставленная
обратная задача волноводного рассеяния в этих случаях не является корректной.
не является непрерывным
(не выполняется третье требование корректности). Таким образом, поставленная
обратная задача волноводного рассеяния в этих случаях не является корректной.
Линейность
задачи понимается в смысле линейной зависимости ![]() от
от ![]() в (1). В выражении (1): A
– линейный интегральный оператор с ядром Φ(β′, γ);
в (1). В выражении (1): A
– линейный интегральный оператор с ядром Φ(β′, γ); ![]() – оператор обратный к A,
– оператор обратный к A,
![]() – функция
спектральной плотности статистических нерегулярностей (ФСП) – функция
относительно которой решается обратная задача,
– функция
спектральной плотности статистических нерегулярностей (ФСП) – функция
относительно которой решается обратная задача, ![]() – рассеянная на нерегулярностях волновода
мощность (например, коэффициент затухания); β – продольная
составляющая постоянных распространения мод рассеяния, формирующих диаграмму
рассеяния; γ – эффективный
показатель преломления или коэффициент
фазового замедления, показывающий, во сколько раз фазовая скорость волны,
распространяющейся по оси z, меньше скорости света в вакууме. Ядро Φ
– это волноводный оптический фактор (оптическая передаточная функция волновода).
Если все же оператор
– рассеянная на нерегулярностях волновода
мощность (например, коэффициент затухания); β – продольная
составляющая постоянных распространения мод рассеяния, формирующих диаграмму
рассеяния; γ – эффективный
показатель преломления или коэффициент
фазового замедления, показывающий, во сколько раз фазовая скорость волны,
распространяющейся по оси z, меньше скорости света в вакууме. Ядро Φ
– это волноводный оптический фактор (оптическая передаточная функция волновода).
Если все же оператор ![]() существует,
но нет устойчивости решения, то это делает обычно невозможной физическую
интерпретацию результатов измерений, поскольку условие устойчивости является
следствием физической детерминированности поставленной задачи волноводного
рассеяния света.
существует,
но нет устойчивости решения, то это делает обычно невозможной физическую
интерпретацию результатов измерений, поскольку условие устойчивости является
следствием физической детерминированности поставленной задачи волноводного
рассеяния света.
Таким образом, возникают две основные проблемы. Что понимать под решением поставленной обратной задачи волноводного рассеяния? Как построить такой алгоритм нахождения приближенного решения задачи, который обладает устойчивостью к малым изменениям во входных данных, например, в диаграмме рассеяния, по которой восстанавливается функция спектральной плотности и/или автокорреляционная функция (АКФ) нерегулярностей (являющаяся преобразованием Фурье ФСП).
Решение первой проблемы позволяет удовлетворить первому требованию корректности (существование решения). Для решения второй проблемы, как правило, используется дополнительная информация об искомом решении [23-26]. Эта дополнительная информация должна отражать сущность рассматриваемого физического явления – в нашем случае – явления волноводного рассеяния света. Такая информация имеет количественный (например, погрешность измерения) или качественный характер (например, гладкость, монотонность, не отрицательность решения и др.). Эта дополнительная информация должна быть учтена при построении математической модели решения обратной задачи.
В обоих случаях с математической точки зрения фактически появляется возможность сузить класс возможных приближенных решений обратной задачи волноводного рассеяния. В первом случае – до компактного множества [23-27]. Во втором – множество возможных приближенных решений (класс допустимых функций) часто не является компактным, а, кроме того, изменения правой части уравнения (1) при не точных входных данных (особенно при высоком уровне шума) могут выводить ее значения за пределы множества, на котором правая часть определена. В обоих случаях удается сделать сформулированную некорректную обратную задачу волноводного рассеяния устойчивой к малым изменениям во входных данных (в измеряемой в дальней зоне диаграмме рассеяния света).
Отметим, что есть ряд методов решения линейных обратных задач, например, метод сравнения [25], метод подбора Тихонова [25], метод квазирешения Иванова [25], метод Бейкуса-Гилберта [23], метод регуляризации Тихонова [25] и др. Метод сравнения, например, является наиболее часто применяемым экспериментаторами для решения различных обратных задач.
Линейная
обратная задача рассеяния в статистически нерегулярном интегрально-оптическом
волноводе при известных показателях преломления образующих волновод сред и
известном коэффициенте фазового замедления формулируется следующим образом: по
измеренной в ближней, промежуточной или дальней зоне диаграмме рассеяния лазерного
излучения восстановить функцию спектральной плотности и/или автокорреляционную
функцию нерегулярностей и определить соответствующие параметры нерегулярностей.
К последним, как правило, относятся геометрические параметры нерегулярностей:
среднеквадратичная высота шероховатостей σ границ раздела сред
волновода и радиус корреляции нерегулярностей r; а также
оптические параметры нерегулярностей, например, волноводного слоя:
среднеквадратичное отклонение показателя преломления волноводного слоя от
среднего значения ![]() и
радиус корреляции неоднородностей показателя преломления волноводного слоя
и
радиус корреляции неоднородностей показателя преломления волноводного слоя ![]() .
.
При постановке двухмерной задачи волноводного рассеяния в виде (1) использован переход от полевой постановки обратной задачи (требующей знания амплитудно-фазового распределения) к постановке задачи, требующей знания распределения интенсивности (2D-диаграммы рассеяния) P(β, γ) рассеянного в волноводе лазерного излучения (см. рис. 1).
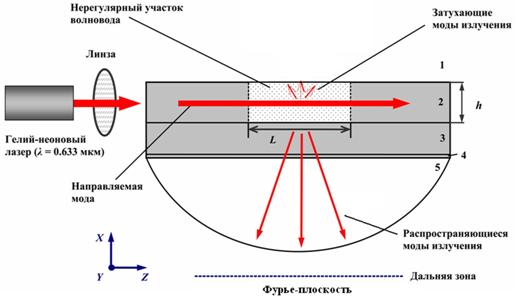
Рис. 1. Схема, иллюстрирующая рассеяние лазерного излучения в
нерегулярном интегрально-оптическом волноводе:
1 – покровный слой
(воздух), 2 – волноводный слой; 3 – подложка; 4 –
иммерсия; 5 – кварцевая полусфера; L
– длина нерегулярной области;
h – толщина волновода.
Таким
образом, весь ход решения сформулированной задачи можно свести к следующему ряду
этапов: 1) в дальней зоне или в некоторой эквивалентной ей плоскости Фурье[1]
на ограниченном участке постоянных распространения ![]() мод
излучения (непрерывного спектра, см. рис. 2) измеряется точечным фотодетектором
(или матрицей, обладающей соответствующим разрешением) 2D-диаграмма
рассеяния
мод
излучения (непрерывного спектра, см. рис. 2) измеряется точечным фотодетектором
(или матрицей, обладающей соответствующим разрешением) 2D-диаграмма
рассеяния ![]() ; 2) на этом ограниченном участке постоянных
распространения
; 2) на этом ограниченном участке постоянных
распространения ![]() определяется
оценка ФСП
определяется
оценка ФСП ![]() ;
3) из
;
3) из ![]() определяются
грубые оценки параметров нерегулярностей; 4) используя теорему Винера-Хинчина, находится
приближенный вид автокорреляционной функции нерегулярностей
определяются
грубые оценки параметров нерегулярностей; 4) используя теорему Винера-Хинчина, находится
приближенный вид автокорреляционной функции нерегулярностей ![]() , где
, где ![]() , z
и z' – координаты в плоскости волновода (вдоль оси z
распространяется направляемая мода); 5) из
, z
и z' – координаты в плоскости волновода (вдоль оси z
распространяется направляемая мода); 5) из ![]() определяются улучшенные оценки параметров;
6)
определяются улучшенные оценки параметров;
6) ![]() используется
для нахождения регуляризованной функции
используется
для нахождения регуляризованной функции ![]() ; 7) из
; 7) из ![]() определяются с высоким разрешением
параметры нерегулярностей.
определяются с высоким разрешением
параметры нерегулярностей.
На
соответствующих этапах решения обратной задачи может быть использована
следующая коррекция решения: оценки ![]() ,
, ![]() или
или ![]() используется для нахождения все более
точного вида ФСП и АКФ.
используется для нахождения все более
точного вида ФСП и АКФ.
Рассмотрим последовательно основные этапы решения поставленной двухмерной задачи волноводного рассеяния лазерного излучения.
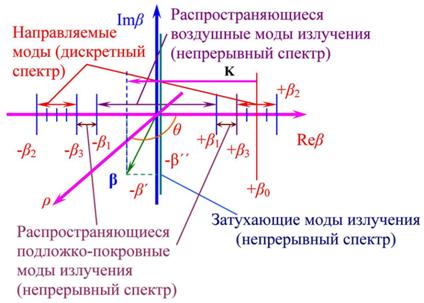
Рис. 2. Диаграмма постоянных распространения направляемых мод ![]() и мод излучения
и мод излучения ![]() нерегулярного
несимметричного волновода, иллюстрирующая процесс рассеяния лазерного
излучения на нерегулярностях волновода. Здесь:
нерегулярного
несимметричного волновода, иллюстрирующая процесс рассеяния лазерного
излучения на нерегулярностях волновода. Здесь: ![]() ,
, ![]() ,
, ![]() ,
, ![]() , где
, где ![]() – показатели преломления воздуха
(обрамляющая среда), волноводного слоя и подложки соответственно,
– показатели преломления воздуха
(обрамляющая среда), волноводного слоя и подложки соответственно, ![]() ;
; ![]() – коэффициент замедления
волновода;
– коэффициент замедления
волновода; ![]() –
некоторая постоянная распространения мод излучения с составляющими
–
некоторая постоянная распространения мод излучения с составляющими ![]() и
и ![]() (в общем случае – комплексная);
(в общем случае – комплексная); ![]() – некоторый продольный
(латеральный) вектор решетки в спектре нерегулярностей.
– некоторый продольный
(латеральный) вектор решетки в спектре нерегулярностей.
1-й этап. Запишем выражение (1) для интенсивности рассеянного в волноводе лазерного излучения в следующем виде:
где C0 – нормировочный множитель; ![]() – передаточная функция
фотодетектора; β, β' – продольная составляющая
постоянной распространения мод излучения, формирующих диаграмму рассеяния на
нерегулярностях. Формула (2) описывает интегральное волноводное рассеяние.
– передаточная функция
фотодетектора; β, β' – продольная составляющая
постоянной распространения мод излучения, формирующих диаграмму рассеяния на
нерегулярностях. Формула (2) описывает интегральное волноводное рассеяние.
При исследовании статистических нерегулярностей обычно измеряется интенсивность диаграммы рассеяния с помощью «точечного» фотодетектора (с достаточно малой апертурой), у которого передаточная функция является дельта функцией δ(β' – β). Тогда формула (2) переходит в выражение, описывающее дифференциальное волноводное рассеяние:
Диаграмма
рассеяния света ![]() измеряется
в дальней зоне (зоне дифракции Фраунгофера или в эквивалентной ей плоскости
Фурье [17-19]) на некотором ограниченном отрезке оси действительных постоянных
распространения мод излучения β (непрерывный спектр),
соответствующих наблюдаемым излучательным подложко-покровным модам и модам
подложки несимметричного или наблюдаемым покровным модам симметричного
волновода соответственно.
измеряется
в дальней зоне (зоне дифракции Фраунгофера или в эквивалентной ей плоскости
Фурье [17-19]) на некотором ограниченном отрезке оси действительных постоянных
распространения мод излучения β (непрерывный спектр),
соответствующих наблюдаемым излучательным подложко-покровным модам и модам
подложки несимметричного или наблюдаемым покровным модам симметричного
волновода соответственно.
По условию задачи измеряемая диаграмма рассеяния – это действительная однозначная функция действительной переменной β (или соответствующего угла рассеяния θ), непрерывная на рассматриваемом отрезке постоянных распространения. Переход от β к углу рассеяния θ в (3) осуществляется в соответствии с равенством β = knicosθ, где ni – показатель преломления среды, где производится измерение. С физической точки зрения непрерывность диаграммы рассеяния (3) является следствием ограниченности интервала, где есть нерегулярности. Ограниченный интервал, очевидно, не может содержать бесконечно протяженных гармонических решеток (формирующих в совокупности случайную нерегулярность), которые могли бы обусловить дельта подобные выбросы (разрывы) в целом непрерывной диаграммы рассеяния. С другой стороны непрерывность диаграммы связана со статистическим характером нерегулярностей.
2-й
этап. Определение оценки функции
спектральной плотности ![]() из измеренной диаграммы дифференциального
волноводного рассеяния (3) проводится по формуле:
из измеренной диаграммы дифференциального
волноводного рассеяния (3) проводится по формуле:
где волноводный оптический фактор ![]() рассчитывается
на компьютере. ФСП определенная по обладающей указанными выше свойствами
диаграмме рассеяния будет также непрерывной функцией действительной переменной β.
Затем используется разложение восстановленной в ограниченном диапазоне
рассчитывается
на компьютере. ФСП определенная по обладающей указанными выше свойствами
диаграмме рассеяния будет также непрерывной функцией действительной переменной β.
Затем используется разложение восстановленной в ограниченном диапазоне ![]() в
усеченный ряд Тейлора (с центром в точке βs):
в
усеченный ряд Тейлора (с центром в точке βs):
где m = 0, 1, 2, …, N << ∞; βm = m∙Δβ; Fm = F(βs) = <P(βs, γ)∙Ф-1(βs, γ)>(m) – коэффициенты разложения, вычисляемые в точке βs внутри некоторого интервала (-βa, +βb) постоянных распространения мод излучения; верхний индекс m означает m-ю производную. Ряд (5) позволяет аналитически продолжить действительную функцию спектральной плотности выше граничной пространственной частоты βmax (выше которой волноводный оптический фактор обращается в ноль). С физической точки зрения ограниченность области определения ФСП связана с практической трудностью измерения диаграммы рассеяния вне отрезка наблюдаемых мод рассеяния, поскольку выше граничной пространственной частоты βmax волноводный оптический фактор волновода, а, следовательно, и диаграмма рассеяния обращается в ноль.
Минимальная
погрешность, достижимая при аппроксимации неограниченно-протяженной ФСП из
класса функций L2(-∞,
+∞) с помощью финитных функций из класса L2(-β, +β), восстановленных при решении обратной задачи волноводного
рассеяния ограничена сверху некоторой величиной ![]() :
: ![]() . Эта величина имеет максимум
приблизительно при N = 13, после которого она достаточно быстро убывает,
стремясь к 0 при N > 25. Константа K
ограничивает сверху (по модулю) величину производных в ряде (5).
. Эта величина имеет максимум
приблизительно при N = 13, после которого она достаточно быстро убывает,
стремясь к 0 при N > 25. Константа K
ограничивает сверху (по модулю) величину производных в ряде (5).
3-й
этап. Из ФСП ![]() определяются оценки параметров
нерегулярностей, например, в соответствии с формулами, приведенными в работах [17-19,
21, 22].
определяются оценки параметров
нерегулярностей, например, в соответствии с формулами, приведенными в работах [17-19,
21, 22].
4-й
этап. Из оценки ![]() находится приближенный
вид автокорреляционной функции нерегулярностей
находится приближенный
вид автокорреляционной функции нерегулярностей ![]() в результате преобразования
Фурье функции спектральной плотности (теорема Винера-Хинчина) в соответствии с
формулой:
в результате преобразования
Фурье функции спектральной плотности (теорема Винера-Хинчина) в соответствии с
формулой:
где β0 = ![]() – модуль продольной составляющей
– модуль продольной составляющей ![]() вектора
распространения
вектора
распространения ![]() волноводной моды вдоль оси Z,
волноводной моды вдоль оси Z,
![]() –
угол падения моды на границу раздела волновода; u = z – z',
z и z' – координаты в плоскости подложки волновода.
–
угол падения моды на границу раздела волновода; u = z – z',
z и z' – координаты в плоскости подложки волновода.
Поскольку оценка АКФ (6) определена на конечном отрезке [0, L], где расположены нерегулярности, она является квадратично интегрируемой (по модулю в квадрате), т.е. принадлежит пространству функций интегрируемых по модулю в квадрате L2 [23-26]. Это означает, что конечен интеграл:
Таким
образом, интервал определения АКФ оказывается ограниченным вполне естественным
образом: вне нерегулярного участка волновода ![]() обращается в ноль
обращается в ноль
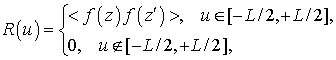
поскольку там по предположению нет нерегулярностей, т.е. АКФ является финитной функцией. Между последними и целыми функциями существует тесная связь [26, 27].
В
соответствии с теоремой Винера-Пэли преобразование Фурье такой функции
допускает аналитическое продолжение ФСП на всю комплексную плоскость до целой
функции конечной степени не выше L/2. Если при |u|
→ ∞ функция |R(u)| < R0exp(-b0|u|),
то функция ![]() будет
аналитической в полосе |β′′| < b0.
будет
аналитической в полосе |β′′| < b0.
Теорема
Винера-Пэли позволяет использовать в качестве конструктивной процедуры
построения аналитического продолжения ФСП за пределы области его определения
комплексный ряд Тейлора типа (5), где берется комплексное значение ![]() , β′ –
это вещественная часть комплексного
, β′ –
это вещественная часть комплексного ![]() , т.е. то β, которое обычно
рассматривается, а β′′ – это мнимая часть
, т.е. то β, которое обычно
рассматривается, а β′′ – это мнимая часть ![]() . При этом в основе
построенной таким образом ФСП будут лежать ее значения, определенные на некотором
отрезке действительной оси постоянных распространения β. Затем в
расчетах может быть использована, например, только действительная или мнимая
части экстраполированного спектра.
. При этом в основе
построенной таким образом ФСП будут лежать ее значения, определенные на некотором
отрезке действительной оси постоянных распространения β. Затем в
расчетах может быть использована, например, только действительная или мнимая
части экстраполированного спектра.
Комплексная ФСП может позволить оценить фазовое распределение, характеризующее весь ансамбль нерегулярностей в целом, а не какую-либо его отдельную реализацию. Используя физическую обоснованность перехода на комплексную плоскость постоянных распространения β, можно в этом случае воспользоваться развитым аппаратом теории аналитических (и в частности – целых) функций, преобразования Фурье и теорем Винера-Хинчина и Винера-Пэли.
Заметим,
что ограничение типа (7) должно быть наложено и на функцию ![]() (или
(или ![]() ), т.к. полная энергия рассеянного
света конечна.
), т.к. полная энергия рассеянного
света конечна.
5-й
этап. Из найденной оценки ![]() в (6) определяются
более точные, чем на 3-м этапе оценки параметров нерегулярностей.
в (6) определяются
более точные, чем на 3-м этапе оценки параметров нерегулярностей.
6-й
этап. Из полученной оценки АКФ ![]() в виде (6)
восстанавливается регуляризованная
в виде (6)
восстанавливается регуляризованная ![]() , наиболее близкая (в определенном смысле)
к заданной АКФ:
, наиболее близкая (в определенном смысле)
к заданной АКФ:
где использованы процедуры классической регуляризации [25] и
квазиоптимальной фильтрации [18, 19,
21, 22], которая позволяет управлять
разрешающей способностью метода, т.к. пространственные составляющие в спектре
нерегулярностей ![]() сглаживаются
на интервале различной длины в зависимости от величины параметра m.
В (8): μ – параметр регуляризации; стабилизаторы p-го
порядка M могут
быть взяты в виде β2p или (β0 – β)2p,
где p ≥ 0 – порядок регуляризации;
сглаживаются
на интервале различной длины в зависимости от величины параметра m.
В (8): μ – параметр регуляризации; стабилизаторы p-го
порядка M могут
быть взяты в виде β2p или (β0 – β)2p,
где p ≥ 0 – порядок регуляризации; ![]() –
комплексно-сопряженное к
–
комплексно-сопряженное к ![]() ;
; ![]() – сглаживающая функция, которая
подбирается, например, из условия минимума среднеквадратичной ошибки решения
обратной задачи.
– сглаживающая функция, которая
подбирается, например, из условия минимума среднеквадратичной ошибки решения
обратной задачи.
7-й этап. Из регуляризованной АКФ (8) определяются с высоким разрешением параметры нерегулярностей [21, 22, 30-33].
3. ПРОБЛЕМА КОРРЕКТНОСТИ РЕШЕНИЯ ОБРАТНОЙ ЗАДАЧИ ВОЛНОВОДНОГО РАССЕЯНИЯ ЛАЗЕРНОГО ИЗЛУЧЕНИЯ
3.1. Доказательство существования решения обратной задачи
Теорема 1. Решение поставленной обратной задачи теории волноводного рассеяния лазерного излучения существует и может быть представлено в виде ряда Тейлора (5).
Для доказательства теоремы подставим усеченный ряд Тейлора (5) в (2), получим следующее интегральное выражение
=
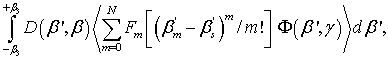 (9)
(9)
которое при передаточной функции ![]() переходит очевидным образом в
переходит очевидным образом в
По условию
решения задачи функция ![]() – это ряд Тейлора, который определен на
ограниченном отрезке постоянных распространения
– это ряд Тейлора, который определен на
ограниченном отрезке постоянных распространения ![]() , т.е. является степенным рядом,
(бесконечно) дифференцируемым на отрезке (в круге – в случае комплексного ряда)
сходимости
, т.е. является степенным рядом,
(бесконечно) дифференцируемым на отрезке (в круге – в случае комплексного ряда)
сходимости ![]() ,
где R > 0. Это разложение функции
,
где R > 0. Это разложение функции ![]() в степенной ряд единственно, а
ряд Тейлора этой функции является аналитической функцией.
в степенной ряд единственно, а
ряд Тейлора этой функции является аналитической функцией.
Функция ![]() по определению является
непрерывной финитной функцией, определенной на том же ограниченном отрезке
постоянных распространения
по определению является
непрерывной финитной функцией, определенной на том же ограниченном отрезке
постоянных распространения ![]() . Следовательно, их произведение (10) –
функция
. Следовательно, их произведение (10) –
функция ![]() –
является действительной (ряд Тейлора рассматривается на действительной оси β)
однозначной в силу однозначности
–
является действительной (ряд Тейлора рассматривается на действительной оси β)
однозначной в силу однозначности ![]() и
и ![]() функцией и, кроме того, – непрерывной на
рассматриваемом отрезке постоянных распространения в силу непрерывности функций
функцией и, кроме того, – непрерывной на
рассматриваемом отрезке постоянных распространения в силу непрерывности функций
![]() и
и ![]() .
.
Таким
образом, полученная функция (10) будет удовлетворять основным требованиям для
диаграммы рассеяния, полученным при анализе условий ее измерения на первом
этапе решения обратной задачи. При N → ∞ усеченный
ряд Тейлора перейдет в ряд (5), а диаграмма ![]() перейдет в
перейдет в ![]() , т.е. будет принадлежать множеству функций
, т.е. будет принадлежать множеству функций
![]() , определяющих
диаграммы рассеяния; I – множество натуральных чисел.
, определяющих
диаграммы рассеяния; I – множество натуральных чисел.
Диаграмма
рассеяния ![]() тем
точнее будет соответствовать некоторой функции
тем
точнее будет соответствовать некоторой функции ![]() из допустимого множества решений
из допустимого множества решений ![]() , чем ýже
исходный спектр нерегулярностей, в противном случае необходимо использовать
процедуру аналитического продолжения найденного
, чем ýже
исходный спектр нерегулярностей, в противном случае необходимо использовать
процедуру аналитического продолжения найденного ![]() на всю ось
на всю ось ![]() . Этим завершается доказательство Теоремы
1.
. Этим завершается доказательство Теоремы
1.
3.2. Доказательство единственности решения обратной задачи
Теорема 2. В классе целых функций поставленная обратная задача теории волноводного рассеяния имеет единственное решение.
Напомним, что целой функцией называется однозначная аналитическая во всей комплексной плоскости (за исключением бесконечно удаленной точки) функция комплексного переменного, представимая всюду сходящимся степенным рядом [26, 27, 29]. Доказательство проведем традиционным способом «от противного».
Пусть
существуют два различных решения ![]() и
и ![]() , удовлетворяющие уравнению (3), и, следовательно, выполняется
тождество:
, удовлетворяющие уравнению (3), и, следовательно, выполняется
тождество:
откуда следует очевидное тождество:
Случай, когда ![]() ,
является тривиальным, поскольку тогда согласно (11) рассеяние будет
отсутствовать в зоне регистрации при любом β во всем диапазоне
наблюдаемых мод излучения (-β3, +β3).
Очевидно, что реальный нерегулярный участок волновода со статистическими
нерегулярностями будет излучать широкий спектр мод излучения, поэтому всегда
можно найти некоторый отрезок оси постоянных распространения [-βa, +βb]
,
является тривиальным, поскольку тогда согласно (11) рассеяние будет
отсутствовать в зоне регистрации при любом β во всем диапазоне
наблюдаемых мод излучения (-β3, +β3).
Очевидно, что реальный нерегулярный участок волновода со статистическими
нерегулярностями будет излучать широкий спектр мод излучения, поэтому всегда
можно найти некоторый отрезок оси постоянных распространения [-βa, +βb] ![]() (-β3, +β3), где
(-β3, +β3), где ![]() . Тогда на отрезке [-βa, +βb] должно выполняться следующее из (12) тождество:
. Тогда на отрезке [-βa, +βb] должно выполняться следующее из (12) тождество:
![]() . (13)
. (13)
По условию решения поставленной обратной задачи разностная функция в тождестве (13) является целой функцией как разность целых функций [27-30]. Следовательно, из (13) и теоремы единственности для аналитических функций [27, 29] следует, что выполнение тождества (13) обеспечивается также на отрезке (-β3, +β3) и всей действительной оси постоянных распространения β. Тогда из (13) следует доказанное тождество
![]() . (14)
. (14)
Тождество
(14) справедливо при любом ![]() . Таким образом, теорема единственности для
поставленной двухмерной обратной задачи волноводного рассеяния лазерного
излучения на статистических нерегулярностях в классе целых функций полностью
доказана.
. Таким образом, теорема единственности для
поставленной двухмерной обратной задачи волноводного рассеяния лазерного
излучения на статистических нерегулярностях в классе целых функций полностью
доказана.
3.3. Проблема устойчивости решения обратной задачи
Условие устойчивости приближенного решения поставленной нами двухмерной обратной задачи теории волноводного рассеяния к небольшим изменениям во входных данных можно сформулировать в виде следующего известного условия: решение обратной задачи будет устойчивым, если для любого ε > 0 существует δ > 0, такое, что если выполняется неравенство
то выполняется неравенство:
![]() , (16)
, (16)
где индексом «mes» отмечены неточно измеренные в дальней зоне данные ![]() и определенная по ним
ФСП нерегулярностей
и определенная по ним
ФСП нерегулярностей ![]() .
Считается, что условия (15) и (16) справедливы в некоторой окрестности
рассматриваемой точки (β, γ) где решение задачи
существует и оно единственно. При этом должно быть обеспечено выполнение
предельного соотношения: при
.
Считается, что условия (15) и (16) справедливы в некоторой окрестности
рассматриваемой точки (β, γ) где решение задачи
существует и оно единственно. При этом должно быть обеспечено выполнение
предельного соотношения: при ![]() ,
, ![]() , и возмущенное решение задачи переходит в
точное. Как правило, без дополнительных предположений о свойствах решения не
удается построить высокоэффективных алгоритмов решения этой задачи.
, и возмущенное решение задачи переходит в
точное. Как правило, без дополнительных предположений о свойствах решения не
удается построить высокоэффективных алгоритмов решения этой задачи.
Одним из
распространенных методов решения этой проблемы является использование понятия
компактности [23-25, 27,
29, 30]. В этом случае множество допустимых решений
удается выделить достаточно узким (компактным) и в качестве приближенного
решения некорректной обратной задачи волноводного рассеяния света можно
выбирать любой элемент данного компактного множества, сопоставимый по точности
с входными данными. Таким образом, мы ограничиваем множество допустимых решений
![]() некоторым
компактным множеством (компактом); I – множество натуральных
чисел. Тогда решение становится устойчивым к малым изменениям входных данных.
При этом используется информация, носящая количественный характер. Ее
использование приводит к следующим методам решения задачи: подбора,
квазирешения, замены исходного уравнения близким к нему и квазиобращения [25].
некоторым
компактным множеством (компактом); I – множество натуральных
чисел. Тогда решение становится устойчивым к малым изменениям входных данных.
При этом используется информация, носящая количественный характер. Ее
использование приводит к следующим методам решения задачи: подбора,
квазирешения, замены исходного уравнения близким к нему и квазиобращения [25].
При
использовании, например, метода подбора в качестве приближенного решения задачи
может браться точное решение уравнения (2) с приближенно заданной диаграммой
рассеяния. Здесь решение ищется также на компакте, где в качестве приближенного
решения задачи берется функция ![]() , для которой выполняется неравенство:
, для которой выполняется неравенство:
![]() .
.
Для того
чтобы класс допустимых решений F являлся компактом в
соответствии с теоремой Монтеля [27] необходимо и достаточно, чтобы множество
аналитических функций было равномерно ограниченным в области аналитичности,
т.е. для любого замкнутого множества ![]() (
(![]() ,
, ![]() – гладкая граница области F)
точек области аналитичности существует положительное число K,
такое, что любая функция
– гладкая граница области F)
точек области аналитичности существует положительное число K,
такое, что любая функция ![]() удовлетворяет во всех точках множества
удовлетворяет во всех точках множества ![]() неравенству:
неравенству:
![]() . (17)
. (17)
В этом случае множество решений ![]() образует компакт, т.е. любая равномерно
сходящаяся последовательность из этого пространства функций сходится равномерно
к своему пределу, являющемуся функцией из того же класса аналитических функций.
Константа K из
неравенства (17) ограничивает величину производных в ряде (5).
образует компакт, т.е. любая равномерно
сходящаяся последовательность из этого пространства функций сходится равномерно
к своему пределу, являющемуся функцией из того же класса аналитических функций.
Константа K из
неравенства (17) ограничивает величину производных в ряде (5).
В силу
своей непрерывности в области ![]() и аналитичности в открытой области F,
целые функции удовлетворяют условию (15) (принцип максимума модуля) [23,
27] и,
следовательно, решение поставленной обратной задачи волноводного рассеяния
будет устойчиво в классе целых функций. Таким образом, мы доказали, что решение
поставленной двухмерной задачи теории волноводного рассеяния света в
статистически нерегулярном планарном волноводе в классе целых функций
корректно, т.е. удовлетворяет всем трем требованиям корректности.
и аналитичности в открытой области F,
целые функции удовлетворяют условию (15) (принцип максимума модуля) [23,
27] и,
следовательно, решение поставленной обратной задачи волноводного рассеяния
будет устойчиво в классе целых функций. Таким образом, мы доказали, что решение
поставленной двухмерной задачи теории волноводного рассеяния света в
статистически нерегулярном планарном волноводе в классе целых функций
корректно, т.е. удовлетворяет всем трем требованиям корректности.
4. ВЫВОДЫ. ДИСКУССИЯ
При анализе проблемы корректности обратной задачи волноводного рассеяния света мы использовали финитность автокорреляционной функции нерегулярностей. В соответствии с теоремой Винера-Пали преобразование Фурье АКФ, т.е. функция спектральной плотности, может быть представлена рядом Тейлора. Затем ФСП может быть продолжена на комплексную плоскость как целая функции (однозначная аналитическая функция комплексного переменного, представимая всюду сходящимся степенным рядом).
Знание функции
спектральной плотности и всех ее производных (в отсутствие экспериментального
шума и погрешностей вычисления!), по крайней мере, в одной точке позволяет
продолжить ФСП в область, определяемую радиусом сходимости степенного ряда.
Далее, зная функцию спектральной плотности и ее производные вблизи границы
области сходимости, можно определить новые коэффициенты ряда Тейлора и получить
новый степенной ряд, расширяющий область определения функции. Выполняя, таким
образом, процедуру аналитического продолжения можно при точных входных данных
построить функцию спектральной плотности (почти) на всей действительной оси
постоянных распространения ![]() . Полученное решение будет единственно и
устойчиво в классе целых функций.
. Полученное решение будет единственно и
устойчиво в классе целых функций.
По крайней мере, с теоретической точки зрения эта конструктивная процедура построения решения обратной задачи волноводного рассеяния в отсутствие шума выглядит вполне безупречно. Однако очевидно, что эта процедура предполагает также отсутствие погрешностей во всех последующих преобразованиях входных данных. Безусловно, что это трудно обеспечить даже при использовании современных суперкомпьютеров. Следовательно, речь может идти только о приближенном корректном решении обратной задачи волноводного рассеяния.
Аналогичная
процедура решения обратной задачи волноводного рассеяния может быть
реализована, если в качестве финитной функции, заданной на конечном отрезке
постоянных распространения ![]() , взять функцию спектральной плотности.
Действительно, как теоретические ФСП и АКФ, так и многие ФСП и АКФ реальных
физических процессов стремятся к нулю при больших значениях аргументов. Поэтому
только априорная информация, условия эксперимента или некоторые теоретические
предположения модельного характера позволяют рассматривать ту или иную функцию
как финитную, т.е. обращающуюся в нуль вне области определения. Выбор того или
иного решения во многом зависит от конкретных условий поставленной задачи.
, взять функцию спектральной плотности.
Действительно, как теоретические ФСП и АКФ, так и многие ФСП и АКФ реальных
физических процессов стремятся к нулю при больших значениях аргументов. Поэтому
только априорная информация, условия эксперимента или некоторые теоретические
предположения модельного характера позволяют рассматривать ту или иную функцию
как финитную, т.е. обращающуюся в нуль вне области определения. Выбор того или
иного решения во многом зависит от конкретных условий поставленной задачи.
Например, известно, что экстраполяция АКФ в область малых значений радиуса корреляции, определяющую возможность нахождения моментов высоких порядков, является достаточно трудной задачей. Однако именно эта область определяет рассеяние на крупномасштабных (по векторам решеток K) нерегулярностях волновода.
С другой стороны, если при решении обратной задачи волноводного рассеяния будет, например, использована простая аналитическая формула для аппроксимации АКФ в области больших значений радиуса корреляции, то это может привести к ошибкам при анализе волноводного рассеяния на мелкомасштабных нерегулярностях (по векторам решеток K в спектре нерегулярностей).
Оценим
точность для случае использования не зашумленной диаграммы рассеяния с неточно
заданной информацией, когда коэффициенты в ряде Тейлора (5) заданы точно при
всех m ≤ N, но значения после N
пропущены, например, были утеряны при измерениях диаграммы рассеяния или были
недоступны для измерений при данных значениях ![]() . Величина погрешности
. Величина погрешности ![]() ограничена сверху:
ограничена сверху: ![]() причем коэффициенты
ряда Тейлора (5) |Fm| ≤ K. Неравенство для
причем коэффициенты
ряда Тейлора (5) |Fm| ≤ K. Неравенство для ![]() получено из (1) путем перехода от
интегрирования по
получено из (1) путем перехода от
интегрирования по ![]() к
интегрированию по углу рассеяния с использованием свойства остаточного члена
ряда Тейлора в форме Лагранжа. Отметим, что величина погрешности
к
интегрированию по углу рассеяния с использованием свойства остаточного члена
ряда Тейлора в форме Лагранжа. Отметим, что величина погрешности ![]() стремится к 0 при N ≥ 25.
стремится к 0 при N ≥ 25.
Важно
также оценить величину максимально допустимой среднеквадратичной высоты шероховатостей
подложки волновода ![]() .
Используя для этой цели условие компактности (допустимого пространства функций),
получаем, что
.
Используя для этой цели условие компактности (допустимого пространства функций),
получаем, что ![]() будет
ограничена сверху величиной примерно 1000 Å. Понятие компактности
позволяет сузить класс исследуемых нерегулярностей до нерегулярностей,
описываемых достаточно плавными и гладкими функциями. Это условие в частности
ограничивает исследования подложками оптических элементов, применяемых в
лазерной оптике, в интегральной оптике, в системах с высокой плотностью записи
информации, у которых поверхность обработана по высокому классу чистоты.
будет
ограничена сверху величиной примерно 1000 Å. Понятие компактности
позволяет сузить класс исследуемых нерегулярностей до нерегулярностей,
описываемых достаточно плавными и гладкими функциями. Это условие в частности
ограничивает исследования подложками оптических элементов, применяемых в
лазерной оптике, в интегральной оптике, в системах с высокой плотностью записи
информации, у которых поверхность обработана по высокому классу чистоты.
Использование
полученного автором статистического критерия разрешения (связывающего
соотношение неопределенностей Гейзенберга и критерий разрешения Аббе-Рэлея) для
волноводного рассеяния позволило получить следующие диапазоны разрешимых
методом волноводного рассеяния значений радиуса корреляции ![]() и среднеквадратичной высоты
шероховатости
и среднеквадратичной высоты
шероховатости ![]() для
длины волны излучения
для
длины волны излучения ![]() =
0.63 мкм [30]:
=
0.63 мкм [30]: ![]()
![]() мкм,
мкм, ![]() Å.
Å.
Следует также подчеркнуть важность использование фазовой информации [1-3, 22, 23, 26, 30], позволяющее повысить разрешение. При исследовании статистического ансамбля однотипных микрообъектов надо учитывать, что фазовая информация содержится в измеряемой «мощностной» диаграмме рассеяния в дальней зоне (и соответственно в энергетическом спектре) в усредненном запутанном виде. Этот факт должен приниматься во внимание при анализе фазовой проблемы т.к. из-за сложного характера формирования диаграммы рассеяния (как в ближней, так и дальней зонах, или в эквивалентных плоскостях Фурье) при волноводном рассеянии света на статистическом ансамбле нерегулярностей, этот путь сверхразрешения, особенно при наличии высокого шума, пока является трудно реализуемым.
В общем случае статистических нерегулярностей для решения фазовой проблемы могут использоваться пространственная ограниченность объекта и свойства аналитических сигналов, позволяющие найти фазу полевой диаграммы рассеяния с помощью, например, преобразования Гильберта. Как следствие возникает проблема поиска методов измерения амплитудно-фазовых диаграмм рассеяния в ближней, промежуточной и дальней зонах при произвольном уровне шума для различных типов нерегулярностей. Как один из методов решения данной проблемы автором предложено использовать для нахождения фазового распределения ансамбля статистических нерегулярностей волновода восстановленную в обратной задаче аналитически продолженную комплексную ФСП [30].
Необходимо подчеркнуть, что использование фазовой информации позволяет повысить разрешение системы примерно вдвое, т.к. в этом случае в два раза увеличивается число степеней свободы. Аналогичный выигрыш может быть, например, получен при передаче информации только в одном состоянии поляризации (например, при использовании только направляемых ТЕ-мод). Поскольку в пределах фундаментального инварианта информационной емкости оптической системы, т.е. числа полных степеней свободы оптического сигнала (принцип Лауэ), можно изменять соотношение между пространственными, временными и поляризационными степенями свободы, сохраняя неизменным их полное число (теорема Лукоша).
Достижение сверхразрешения в методе волноводного рассеяния возможно также при использовании метода Габора, относящегося к преобразованиям вэйвлетного типа. Здесь существует проблема выбора «удачного» набора базисных функций, по которым производится разложение, и потребность нахождения устойчивых алгоритмов численного обращения матриц, особенно при наличии шумов.
Возможно также применение в качестве набора базисных функций собственных функций преобразования Фурье в конечных пределах (например, в пределах диапазона регистрируемых мод излучения в соответствующей плоскости Фурье), т.е. вытянутых сфероидальных волновых функций. Как известно, эти функции образуют полную систему функций, как на бесконечном, так и на конечном интервалах. При этом они ортогональны на обоих интервалах, т.е. биортогональны. Разлагая входную и выходную функции (например, автокорреляционную функцию нерегулярностей и диаграмму рассеяния в дальней зоне) по полному ортогональному набору сфероидальных волновых функций, получим соотношения, позволяющие решить обратную задачу. При сверхразрешении здесь возникают, по крайней мере, две проблемы: а) наличие шума, б) быстрое уменьшение собственных значений преобразования Фурье.
Учитывая
эти проблемы, необходимо по возможности определять при решении обратной задачи
необходимые функции без интегральных, дифференциальных и др. преобразований.
При этом ограничения измерительной техники (фильтры, фотоприемники, усилители,
аналого-цифровые преобразователи и др.) не должны превышать ограничений
используемой модели изучаемого явления. Несомненно, что при высокоточных
измерениях, особенно при решении проблемы сверхразрешения требуется серьезная
аппаратно-аналитическая обработка данных измерений в соответствии с заранее
разработанным алгоритмом.
5. ЗАКЛЮЧЕНИЕ
В настоящей работе сформулирована и последовательно исследована проблема корректности решения линейной обратной задачи теории рассеяния лазерного излучения в статистически нерегулярном двухмерном интегрально-оптическом волноводе в отсутствие шума.
Приближенное корректное решение поставленной обратной задачи получено путем ограничения множество допустимых решений некоторым компактным множеством. Тогда решение становится устойчивым к малым изменениям входных данных. При этом используется информация о данных рассеяния в дальней зоне, носящая количественный характер.
Компьютерная реализация разработанного метода нахождения решения обратной задачи волноводного рассеяния требует разработки эффективных вычислительных алгоритмов, особенно при решении проблемы сверхразрешения. Несомненно, наилучшего результата можно достичь, если известна какая-либо априорная информация об объекте.
Важным
преимуществом рассмотренного метода исследования является использование явления
волноводного рассеяния, которое позволяет повысить чувствительность измерений
примерно в 100-1000 по сравнению с методами однократного рассеяния света,
благодаря многократному синфазному рассеянию лазерного излучения на исследуемом
статистическом ансамбле нерегулярностей. Волноводный метод позволяет получить
статистическую информацию о шероховатости подложки (или неоднородности
волноводного слоя) оптической интегральной схемы за одно измерение с достаточно
большой площади поверхности (или объема волноводного слоя). Преимуществом
метода является также возможность исследования нерегулярностей волновода в
широком диапазоне изменения их латеральных размеров, включая и размер порядка
длины волны зондирующего излучения, как и в теории рассеяния Ми.
ЛИТЕРАТУРА
1. Маркузе Д. Оптические волноводы. – М.: Мир, 1974.
2. Содха М.С., Гхатак А.К. Неоднородные оптические волноводы. – М.: Связь, 1980.
3. Снайдер А., Лав Дж. Теория оптических волноводов. – М.: Радио и связь, 1987.
4. Marcuse D. Radiation losses of dielectric waveguides in terms or the power spectrum or the wall distortion function // Bell System Tech. J. 1969. V. 48. No. 10. P. 3233-3242.
5. Дерюгин Л.Н., Марчук А.Н., Сотин В.Е. Излучение с плоского диэлектрического волновода // Изв. вузов. Радиоэлектроника. 1970. Т. 13. № 3. С. 309-315.
6. Suematsu Y., Furuya K. Propagation mode and scattering loss of a two dimensional dielectric waveguide with gradual distribution of refractive index // IEEE Trans. on MTT. 1972. V. 20. No. 7. P. 524-531.
7. Tsai T.L., Tuan H.S. Reflection and scattering by a single groove in integrated optics // IEEE J. of QE. 1974. V. 10. No. 3. P. 326-332.
8. Киселев В.А. О распространении, преобразовании и генерации поверхностных световых волн в тонких пленках с гармонически промодулированным показателем преломления // Квантовая Электроника. 1974. Т. 1. № 4. С. 899-907.
9. Прохоров А.М., Спихальский А.А., Сычугов В.А., Шипуло Г.П. Отражение и излучение Н- и Е-волн на гофрированном участке диффузионного волновода // Квантовая Электроника. 1976. Т. 3. № 9. С. 1941-1947.
10. Гудзенко А.И. Резонансное отражение в плоских волноводах с периодической модуляцией толщины диэлектрика // Радиотехника и Электроника. 1976. Т. 21. № 3. С. 451-457.
11. Imai M., Miyanaga S., Asakura T. Mode conversion and radiation loss caused by refractive-index fluctuations in an asymmetric slab waveguide // IEEE J. of QE. 1977. V. 13. No. 4. P.255-262.
12. Дерюгин Л.Н., Комоцкий В.А. Явления при дифракции оптической волны с пространственной фазовой модуляцией на периодической амплитудной решетке // Оптика и Спектроскопия. 1979. Т. 46. Вып. 1. С. 146-152.
13. Андлер Г., Черемискин И.В. Рассеяние в диэлектрическом волноводе со случайными искажениями стенок // Изв. вузов. Радиоэлектроника. 1981. Т. ХХIV. № 9. С. 68-70.
14. Андлер Г., Егоров А.А., Черемискин И.В. Определение параметров шероховатости оптической поверхности по рассеянию в диэлектрическом волноводе // Оптика и Спектроскопия. 1984. Т. 56. № 4. С. 731-735.
15. Сиро Ф. Васкес С. де Ф., Егоров А.А., Черемискин И.В. К вопросу об определении статистических характеристик нерегулярностей тонкопленочных волноводов // Автометрия. 1991. № 2. С. 51-55.
16. Егоров А.А. Характеристики излучения, рассеянного на шероховатостях поверхности подложки планарного волновода // Поверхность. Физика, химия, механика. 1994. № 5. С. 72-76.
17. Egorov A.A. Theory of waveguide optical microscopy // Laser Physics. 1998. V. 8. No. 2. P. 536-540.
18. Yegorov A.A. A new algorithm of restoring the autocorrelation function of subwavelength statistic surface roughness by light scattering in integrated optical waveguide in the presence of a high additive stochastic noise // Proc. SPIE. 2002. V. 4900. P. 792-801.
19. Егоров А.А. Восстановление экспериментальной автокорреляционной функции и определение параметров статистической неровности поверхности по данным рассеяния лазерного излучения в интегрально-оптическом волноводе // Квантовая Электроника. 2003. Т. 33. № 4. С. 335-341.
20. Егоров А.А. Векторная теория рассеяния лазерного излучения в интегрально-оптическом волноводе с трехмерными нерегулярностями при наличии шума // Квантовая Электроника. 2004. Т. 34. № 8. С. 744-754.
21. Egorov A.A. Correct investigation of the statistic irregularities of integrated optical waveguides using waveguide light scattering // Laser Physics. 2004. V. 14. No. 7. P. 987-995.
22. Егоров А.А. Обратная задача рассеяния монохроматического света в статистически нерегулярном волноводе: теория и численное моделирование // Оптика и Спектроскопия. 2007. Т. 103. № 4. C. 638-645.
23. Колтон Д., Кресс Р. Методы интегральных уравнений в теории рассеяния. – М.: Мир, 1987.
24. Арсенин В.Я. Методы математической физики и специальные функции. – М.: Наука, 1974.
25. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. – М.: Наука, 1981.
26. Хургин Я.И., Яковлев В.П. Методы теории целых функций в радиофизике, теории связи и оптике. – М.: Гос. издательство физ.-мат. литературы, 1962.
27. Маркушевич А.И. Краткий курс теории аналитических функций. – М.: Наука, 1978.
28. Анго А. Математика для электро- и радиоинженеров. – М.: Наука, 1965.
29. Свешников А.Г., Тихонов А.Н. Теория функций комплексной переменной. – М.: Физматлит, 2005.
30. Егоров А.А. Автореф. дисс. … д.ф.м.н. Теория и математическое моделирование рассеяния лазерного излучения в нерегулярном интегрально-оптическом волноводе при наличии шума. – М.: РУДН, 2005.
31. Егоров А.А. Теория волноводного рассеяния света в интегрально-оптическом волноводе при наличии шума // Изв. вузов. Радиофизика. 2005. Т. 48. № 1. С. 63-75.
32. Egorov A.A. Super resolution in the waveguide inverse light scattering problem // Journal of Radio Electronics. 2007. No. 6.
33. Egorov A.A. Influence of light scattering by 3d-irregularities on the characteristics of the integrated optical devices using for optical signal processing // Journal of Radio Electronics. N. 2. 2008.
[1] На возможность использования вместо диаграммы рассеяния, измеренной в дальней зоне, соотвествующего энергетического распределения, измеренноого в некоторой эквивалентной плоскости Фурье, автор обращал внимание еще в своих докладах 1980-2000 г.г. на различных семинарах и конференциях РУДН, МНТОРЭС им. А.С. Попова, ИОФАН и др, а также – в своих ранних работах (см., например, [17-19]). Как известно поле в задней фокальной плоскости линзы соответствует дифракционному полю в дальней зоне (зоне дифракции Фраунгофера). Несмотря на то, что этот факт хорошо известен в классической оптике, в интегральной оптике для анализа волноводного рассеяния до нас этим никто не воспользовался. При таком подходе следует помнить, что при измерении амплитудно-фазового распределения в плоскости Фурье потребуется корректный учет фазовых сомножителей в соответствующих комплексных выражениях для полей.
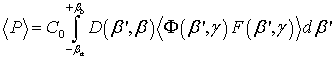 , (2)
, (2)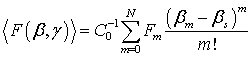 , (5)
, (5)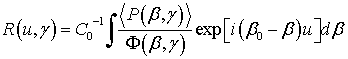 , (6)
, (6)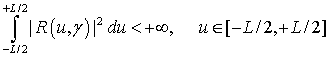 . (7)
. (7)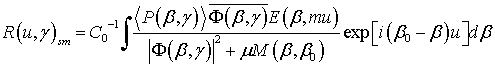 . (8)
. (8)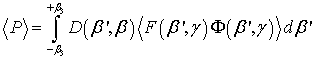
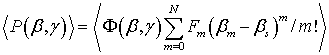 . (10)
. (10)