ИССЛЕДОВАНИЕ
ОСОБЕННОСТЕЙ ДИНАМИКИ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ В МЕТАМАТЕРИАЛАХ ЧИСЛЕННЫМИ МЕТОДАМИ
В. Н. Корниенко, В. А. Черепенин
Институт радиотехники и электроники им. В.А.Котельникова РАН
Получена 28 апреля 2010 г.
Аннотация. В работе представлены результаты численного моделирования динамики электромагнитного поля в средах, диэлектрические и магнитные проницаемости которых могут принимать отрицательные значения. Показано, что в некоторых случаях в моделях, основанных на усредненных характеристиках среды, которые не имеют зависимости от времени (не обладают частотной дисперсией), может нарушаться принцип причинности и закон сохранения энергии.
Ключевые слова: метаматериалы, численное моделирование.
Введение
В последнее время повышенный интерес
вызывают экспериментальные и теоретические исследования специфических
электромагнитных свойств так называемых метаматериалов. Количество статей по
этой тематике достаточно велико ([1]), и проведение обзора полученных
результатов – отдельная и весьма сложная задача. Мы обратим внимание только на
одну из многочисленных проблем: проблему описания динамики электромагнитного
поля в таких средах [2]. К настоящему моменту существует множество вопросов о
возможности применимости тех или иных подходов к построению теоретических
моделей: можно ли использовать понятия диэлектрической (![]() ) и магнитной (
) и магнитной (![]() ) проницаемости, следует и, если следует, то в какой мере,
учитывать частотную дисперсию этих величин и пр.
) проницаемости, следует и, если следует, то в какой мере,
учитывать частотную дисперсию этих величин и пр.
Целью
данной работы является демонстрация при помощи методов вычислительного
эксперимента на нескольких примерах ограниченности часто используемых моделей
для непрерывных неоднородных сред без частотной дисперсии с постоянными ![]() и
и ![]() , которые могут принимать
отрицательные значения.
, которые могут принимать
отрицательные значения.
Постановка задачи
Рассмотрим
двумерную прямоугольную область V (рис.1.), заполненную средой с ![]() ,
, ![]() и проводимостью
и проводимостью ![]() . Введем декартову систему координат, начало которой
совпадает с левым нижним углом области V.
. Введем декартову систему координат, начало которой
совпадает с левым нижним углом области V.

Рис.1. Рассматриваемая система.
В точке ![]() с координатами
с координатами ![]() расположим точечный источник
электромагнитного поля, характеризующийся плотностью тока с заданной временной
зависимостью:
расположим точечный источник
электромагнитного поля, характеризующийся плотностью тока с заданной временной
зависимостью:
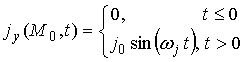 (1)
(1)
Такой источник может
возбуждать в рассматриваемой пространственной области три компоненты
электромагнитного поля: ![]() .
.
Описание динамики поля будем проводить, используя два уравнения Максвелла в пространственно-временном представлении и пару материальных уравнений, справедливых для непрерывных изотропных линейных сред:
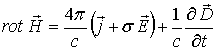 (2)
(2)
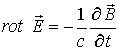 (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
Так как диэлектрическая и магнитная проницаемости не зависят от времени и отличны от нуля, то, с учетом выбранной плотности тока (1), для двумерного случая запишем систему уравнений (2)-(5) в следующем виде:
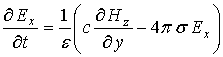 (6)
(6)
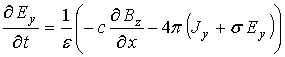 (7)
(7)
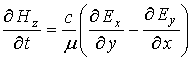 (8)
(8)
Предположим, что на временном интервале ![]() поле в системе отсутствует, что позволяет, выбрав в качестве
начального момента времени
поле в системе отсутствует, что позволяет, выбрав в качестве
начального момента времени ![]() , использовать для (6)-(8) нулевые
начальные условия.
, использовать для (6)-(8) нулевые
начальные условия.
Для системы (6)-(8) будем рассматривать два вида граничных условий:
1) случай идеально проводящих границ (что соответствует случаю прямоугольного резонатора с бесконечной добротностью);
2) случай, при котором границы области, перпендикулярные оси x выбранной системы координат, являются прозрачными для излучения, а на границах, перпендикулярных оси y поле имеет структуру плоской волны, распространяющейся вдоль y.
Во втором случае условие излучения реализуем путем введения в небольшой области вблизи границ искусственного согласованного поглотителя.
Численная схема
Рассматриваемую систему уравнений (6)-(8) с выбранными начальными и
граничными условиями будем решать численно, основываясь на методе конечных
разностей [3]. В V введем три пространственные сетки, в
узлах которых будут определяться значения ![]() . Пусть индекс i соответствует номеру узла сетки по направлению оси x, а j – по направлению оси y. Тогда координаты узлов пространственных сеток задаются
следующими выражениями:
. Пусть индекс i соответствует номеру узла сетки по направлению оси x, а j – по направлению оси y. Тогда координаты узлов пространственных сеток задаются
следующими выражениями:
для компоненты ![]() -
- ![]()
![]() ;
;
для компоненты ![]() -
- ![]()
![]() ;
;
для компоненты ![]() -
- ![]()
![]() .
.
Здесь ![]() ,
, ![]() ,
, ![]() и
и ![]() - шаги пространственных сеток по x и y
соответственно. Далее положим
- шаги пространственных сеток по x и y
соответственно. Далее положим ![]() .
.
Интегрирование по времени будем выполнять с шагом ![]() , величина которого удовлетворяет условию Куранта:
, величина которого удовлетворяет условию Куранта:
![]()
где ![]() - максимальная фазовая скорость волны в среде,
- максимальная фазовая скорость волны в среде, ![]() .
.
Учитывая, что компоненты магнитного поля вычисляются в моменты времени,
сдвинутые на ![]() /2 относительно моментов времени, в
которых находим
/2 относительно моментов времени, в
которых находим ![]() и
и ![]() , конечно-разностная аппроксимация уравнений (6)-(8) имеет
вид:
, конечно-разностная аппроксимация уравнений (6)-(8) имеет
вид:
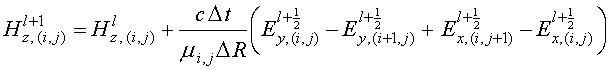 (9)
(9)
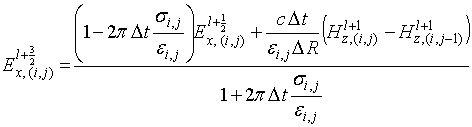 (10)
(10)
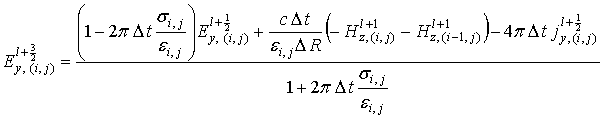 (11)
(11)
Здесь верхний индекс
обозначает момент времени, нижние – компоненту поля и номер узла сетки.
Значения ![]() ,
, ![]() и
и ![]() берутся в тех же узлах, что и
соответствующие компоненты поля.
берутся в тех же узлах, что и
соответствующие компоненты поля.
Результаты моделирования
1. Пусть V имеет размер 45х45 см, границы
области – идеально проводящие, частота источника составляет ![]() , точка
, точка ![]() имеет координаты
имеет координаты ![]() . Среда, заполняющая область, однородна.
. Среда, заполняющая область, однородна.
Проведем сравнение динамики поля для двух случаев: 1) ![]() ,
, ![]() ,
, ![]() (вакуум); 2)
(вакуум); 2) ![]() ,
, ![]() ,
, ![]() (дважды отрицательная среда без
поглощения).
(дважды отрицательная среда без
поглощения).
На рис.2. показаны результаты численного моделирования динамики электромагнитного поля для этих двух случаев. Цвет указывает на величину поля (белый – максимальная, черный – минимальная).
Рис.2. Эволюция пространственного распределения магнитного поля для вакуума (а)
и дважды отрицательной среды (б)
Как следует из представленных результатов, в обоих случаях фазовая скорость возбуждаемой волны одинакова и имеет положительное значение: волна распространяется от источника. Однако, поведение потоков мощности имеет существенное отличие (рис.3): если в первом случае поток мощности поля направлен от источника, то во втором – в противоположную сторону. В принципе, этот результат вполне предсказуем и известен (см., например, [1]). Однако, в отличие от давно известных сред вакуумной электроники, где этот эффект используется, например, в лампе обратной волны [4], здесь не выполняется принцип причинности.
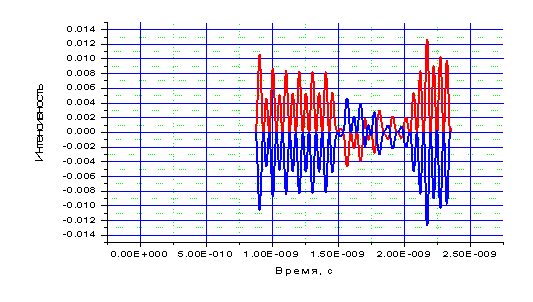
Рис.3. Зависимость x-ой компоненты потока мощности в точке с координатами от времени для вакуума (красная кривая) и дважды отрицательной среды без поглощения (синяя кривая).
Кроме того, реализуется ситуация, при которой энергия черпается из среды
и поглощается в точке источника. Физически это, по-видимому, возможно только
тогда, когда среда обладает запасенной энергией, т.е. активна. Описание таких
сложных сред при помощи только ![]() и
и ![]() проблематично.
проблематично.
2. В простейшей системе, содержащей границу раздела «вакуум – дважды отрицательная среда», наблюдается неограниченный рост амплитуды поля (рис.4.).

для просмотра видео кликните здесь
Рис.4. Эволюция пространственного распределения магнитного поля в неоднородной среде, содержащей границу раздела «вакуум – дважды отрицательная среда».
Ситуация принципиально не изменяется при введении дополнительного поглощения за счет конечной проводимости – изменяется лишь инкремент нарастания поля. Таким образом, в такой системе закон сохранения энергии, по крайней мере в простой форме, не выполняется.
3. Работоспособность используемой численной схемы в случае пространственно неоднородных сред продемонстрируем на следующих примерах.
Рассмотрим задачу распространения волны, создаваемой точечным источником (1) при наличии в системе линзы с радиусом кривизны 40 см.
Пусть в первом случае прямоугольная область описывается диэлектрической и
магнитной проницаемостями, равными единице, и значение ![]() внутри линзы равно 3. Во втором случае среда имеет
внутри линзы равно 3. Во втором случае среда имеет ![]() ,
, ![]() , и значение
, и значение ![]() внутри линзы равно -3.
внутри линзы равно -3.
На рис.5. приведены результаты моделирования для этих двух случаев. Положение формируемого изображения с хорошей точностью совпадает с его координатами, получаемыми из геометрической оптики.

а) для просмотра видео кликните здесь

б)для просмотра видео кликните здесь
Рис.5. Эволюция пространственного распределения магнитного поля в неоднородной среде для вакуума (а) и дважды отрицательной среды (б).
Выводы
Из полученных результатов следует, что модели сред с отрицательными ![]() и
и ![]() следует применять с большой
осторожностью, так как они не удовлетворяют принципу причинности, и в них
энергия черпается из среды.
следует применять с большой
осторожностью, так как они не удовлетворяют принципу причинности, и в них
энергия черпается из среды.
Таким образом, для описания реальных метаматериалов необходимы более сложные модели, в которых бы выполнялись закон сохранения энергии и принцип причинности.
Отметим, что полученный в данной работе результаты в целом согласуются с замечаниями о дважды отрицательных средах, высказанными ранее проф.А.А.Рухадзе на одном из семинаров в ИОФ РАН.
Литература
1. В.М.Агранович, Ю.Н.Гартштейн. //Успехи физ. наук. 2006. Т.176. № 10. С.1051.
2. А.П.Виноградов, А.В.Дорофеенко, С.Зухди. // Успехи физ. наук. 2008. Т.178. № 15. С.511.
3. Управляемый термоядерный синтез //под ред. Дж.Киллина. М.:Мир. 1980.
4. Лебедев И.В. Техника и приборы сверхвысоких частот. Т.II. М.:Высшая школа. 1972.
