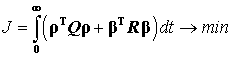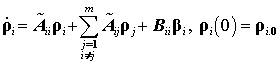Робастная стабилизация состояния параметрически возмущенной активной многопанельной составной отражающей поверхности главного рефлектора радиотелескопа

УДК 62-506

Робастная стабилизация состояния параметрически возмущенной активной многопанельной составной отражающей поверхности главного рефлектора радиотелескопа

М. В. БеловСанкт-Петербургский государственный политехнический университет

Получена 7 апреля 2011 г.

Аннотация. Для активной многопанельной составной отражающей поверхности главного рефлектора большого полноповоротного радиотелескопа миллиметрового диапазона предложены модельные описания как линейной крупномасштабной интервальной динамической системы с параметрическими возмущениями в условиях отсутствия и наличия сильных межпанельных связей. Рассмотрены вопросы синтеза оптимальных асимптотически устойчивых робастных регуляторов в классе централизованных и децентрализованных структур, обеспечивающих стабилизацию состояния множества возмущенных панелей главного зеркала в заданном пространственном положении, соответствующем предписанной форме отражающей поверхности.

Ключевые слова: радиотелескоп, составная отражающая поверхность, крупномасштабная линейная система, интервальные модели, централизованное и децентрализованное управление, робастная стабилизация, асимптотическая устойчивость.

Abstract. It is proposed the model for the active multipanel composite reflecting surface of the main reflector of the large millimeter radio telescope as large linear interval dynamic system with parametric perturbations in the absence and presence of strong interpanel ties. The problem of synthesis of optimal asymptotically stable robust regulator in the class of centralized and decentralized structures to ensure stabilization of the perturbed set of panels of the main reflector in a specified position is discussed.

Key worlds: radio telescope, composite reflecting surface, large linear system, interval models, centralized and decentralized control, robast stabilization, asymptotic stability.

1. Введение

В настоящее время в практике построения больших радиотелескопов миллиметрового диапазона находят применение антенные системы с так называемыми активными (адаптивными) отражающими поверхностями [1,2] – см. рис. 1. Такие поверхности представляют собой составные многоэлементные конструкции, пространственное положение зеркальных пластин в которых регулируется, позволяя с достаточно высокой точностью аппроксимировать параболоид или эллипсоид вращения и компенсировать при этом деформации и линейные возмущения положения отражающих щитов, вызванные гравитационными, термическими и ветровыми воздействиями.

Активные многоэлементные составные зеркальные поверхности больших антенн радиотелескопов в данном случае являются типичным представителем класса крупномасштабных (больших, сложных) динамических систем, поскольку они характеризуются многомерностью (высокой размерностью) фазового вектора и многосвязностью его компонент. Многосвязность здесь отражает сильное влияние друг на друга переменных состояния и управлений в пределах подсистем, а также сильные взаимосвязи между подсистемами. Заметим при этом, что подсистемами у активной отражающей поверхности следует считать зеркальные панели, ее образующие.

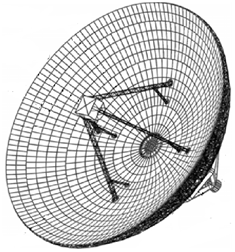
Рис. 1. Главный рефлектор радиотелескопа с активной составной поверхностью.

Функционально радиотелескоп представляет собой двухфокусную радиооптическую систему (рис. 2), закрепленную в двухосном кардановом подвесе.

Радиооптическая система образуется главным рефлектором (ГР) радиотелескопа, контррефлектором (КР), расположенном за фокусом основного зеркала, и приемником (Пр), находящемся в фокусе вторичного рефлектора. На уровень достижимости всеволновости эксплуатации радиотелескопа, т.е. возможностей наблюдения с его помощью миллиметровых и субмиллиметровых космических излучений определяющее влияние оказывает качество предэксплуатационной и текущей динамической юстировки отражающей поверхности главного рефлектора приемной системы.

В соответствии с законами геометрической оптики, излучение, приходящее от наблюдаемых радиоастрономических объектов в форме параллельного пучка, отражаясь от поверхности главного зеркала радиотелеcкопа, поступает в приемник, размещенный в сопряженном фокусе контррефлектора и главного рефлектора.

Рис. 2. Радиооптическая система радиотелескопа.

Условием сохранения синфазности отраженного главным рефлектором излучения является наличие у него идеальной параболической отражающей поверхности при условии таких же свойств у эллипсоидальной поверхности контррефлектора. Однако применение при построении зеркальной системы составных многопанельных отражающих поверхностей, элементы-щиты которой, как и несущая конструкция зеркал, имеют ошибки изготовления и сборки, усугубляемые используемым способом формирования отражающей поверхности, приводят к тому, что реальная составная поверхность аппроксимирует идеальную с некоторой среднеквадратической погрешностью . Вследствие наличия таких отклонений реальной отражающей поверхности от идеальной, синфазность наблюдаемого излучения радиоастрономических объектов нарушается, что приводит к уменьшению реального усиления радиотелескопа.

Исходную форму составному многоэлементному главному зеркалу, максимально близкую к форме идеального параболоида вращения, придают в процессе его предэксплуатационной юстировки после сборки конструкции главного рефлектора. При выполнении этой юстировки считается справедливой сильная гипотеза об абсолютной жесткости и недеформируемости металлоконструкций радиотелескопа, в т.ч. и гипотеза о недеформрруемости отражающих панелей, образующих составной главный рефлектор.

Вместе с тем, очевидно, что в реальных условиях эксплуатации большой полноповоротный радиотелескоп должен функционировать всесезонно, всепогодно, при достаточно больших суточных перепадах температуры окружающей среды, при скоростях ветра до 10 м/с и более. Эти факторы, а также сильные гравитационные воздействия на механическую структуру конструкцию и зеркальные щиты главного рефлектора при перенаправлении центра антенны в различные позиции (особенно его повороты по высоте) приводят к возникновению деформаций металлоконструкций радиотелескопа. Составная поверхность главного рефлектора в этой ситуации теряет свою настроенную в процессе предъэксплуатационной юстировки форму и, как следствие, уменьшается эффективность антенны. Наиболее распространенные искажения формы составной отражающей поверхности схематично изображены на рис. 3 – смещения щитов главного зеркала (а), неровности поверхности панелей возникающие при их неравномерном нагреве (b), искажения пространственного положения пластин, приводящие к несовпадению фокусов главного зеркала и щитов (c). Это означает, что любые дестабилизирующие воздействия, будь то гравитационные, температурные либо ветровые возмущения, в конечном итоге приводят к разъюстировке радиооптической системы радиотелескопа и, как следствие, к ухудшению эффективности его работы и качества приема космических излучений сверхвысоких частот. Следовательно, в реальных условиях эксплуатации сильная гипотеза о недеформируемости металлоконструкций радиотелескопа, в т.ч. конструктивных элементов и отражающих пластин его главного зеркала, неприменима.

Рис. 3. Неидеальности (погрешности) составной отражающей поверхности главного рефлектора: смещение щитов поверхности (а), неровности поверхности панелей при их неравномерном нагреве (b), гравитационные искажения пространственного положения пластин, приводящие к несовпадению фокусных расстояний главного зеркала и щитов (c).

Сказанное предполагает, что радиотелескоп для сохранения хорошей эффективности приема сверхвысокочастотных радиоизлучений космических объектов при воздействии любых возмущений должен иметь такую систему управления положением зеркальных щитов главного рефлектора, которая была бы способна оперативно парировать любые деформирующие перемещения отражающих панелей, удерживая с помощью прецизионных электродомкратов (актуаторов) такое их пространственное состояние, в котором реальное среднеквадратическое отклонение пространственного положения реперных точек зеркальных щитов соответствует условию

где – величина допустимой среднеквадратичной погрешности

Величина допустимой среднеквадратичной погрешности может быть определена по следующей формуле [3]:

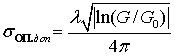, (1)

где , – усиление, соответственно, реальной и «идеальной» главной антенны радиотелескопа, при этом , – длина волны наблюдаемого излучения, – эффективная площадь главного рефлектора.

Как правило, при проектировании систем управления крупномасштабными динамическими объектами, к каковым и относится описанная составная отражающая поверхность, точные значения их параметров неизвестны, а известны только оценки этих параметров в виде верхних и нижних граничных значений либо задана принадлежность параметров некоторому множеству. Кроме того параметры объекта управления могут изменяться в процессе функционирования. По этим причинам проектируемые регуляторы должны обеспечивать устойчивость и качество не одного объекта управления, а целого класса таковых объектов. Это достигается путем придания управляющим средствам свойств робастной устойчивости и робастного качества по отношению к параметрическим и иным возмущающим воздействиям за счет синтеза соответствующих управляющих алгоритмов. Также следует отметить, что умеренные отклонения пространственного положения зеркальных щитов составной поверхности относительного состояния аппроксимирующего параболоида вращения приводят к необходимости удержания многоэлементного объекта управления в заданной области допустимых отклонений, ограниченных величиной , а это характеризует данную задачу как задачу стабилизации.

2. Модельные описания составной отражающей поверхности как крупномасштабного объекта управления

Прежде, чем приступать к синтезу робастных законов управления многоэлементной отражающей поверхностью, дадим модельные описание такого многомерного управляемого объекта как крупномасштабной системы.

Пусть эволюционные процессы в подобном управляемом многомерном объекте описываются нелинейным дифференциальным уравнением вида:

, (2)

в котором – вектор фазовых координат, в качестве которых выберем смещения по нормали реперных точек составной пространственной конструкции от некоторой эталонной параболической поверхности стабилизации главного рефлектора; – вектор управлений, характеризующий состояние механизмов регулирования положением щитов составной поверхности; – векторная функция, – вещественные функции, определенные и непрерывные по совокупности аргументов в области

Пусть уравнение (2) описывает отклонения фазовых координат нелинейного объекта управления от стационарного состояния , соответствующего состоянию вектора пространственных координат реперных точек, совпадающим с вектором точек, находящихся на поверхности стабилизации , при этом объект управления (составная поверхность) удерживается в состоянии с помощью стабилизирующего управляющего воздействия . Тогда, используя в окрестности стационарной точки интервальные расширения формулы Тейлора для функции вида [4]

, (3)

где есть интервальное расширение полинома Тейлора

;

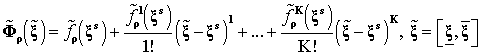а интервальное расширение остатка равно

;

преобразуем уравнение (2) к квазилинейному интервальному виду

. (4)

Здесь интервальные матрицы и есть совокупность коэффициентов ; ; 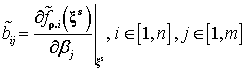соответственно; которые вычисляются в стационарной точке .

Если положить, что для точек справедливы неравенства

и принять, что выполнима оценка

, (5)

то для синтеза управления, стабилизирующего систему (4) в окрестности стационарной точки , обычно используется следующее интервальное уравнение эволюции крупномасштабной системы:

, (6)

которое есть совокупность множества «точечных» подсистем

(7)

с параметрами из заданных интервалов и .

При синтезе робастного управления зачастую удобно иметь математическую модель динамической системы в виде двух составляющих – медианной системы, описывающей номинальные режимы, и системы в вариациях, которая характеризует предельно возможные режимы:

, (8)

где , – матрицы медианных (номинальных) зна-чений параметров системы, , ; , – интервальные матрицы вариаций параметров, , .

Если интервальная неопределенность присутствует только при определении элементов матрицы , объект из семейства (6) принимает вид системы с параметрическими возмущениями:

, (9)

в которой – переменная, учитывающая параметрические возмущения.

Заметим, что к аналогичному виду можно привести и любой объект семейства (8), если положить, что , когда

Для уменьшения трудностей вычислительного характера, которые возникают при исследовании крупномасштабных систем, исходная многомерная многосвязная система вида (6) или (9) обычно представляется в виде совокупности взаимосвязанных подсистем меньшей размерности. Для этого используются различные методы декомпозиции [5]: структурная, формальная, временная, по входам (управляющим) или по выходам. Для построения модельного описания составной отражающей поверхности воспользуемся следующими способами членения большой системы на подсистемы – структурной, как вытекающей из физических свойств исследуемого составного многопанельного объекта управления, и декомпозицией по входам, когда каждая из подсистем имеет один управляющий вход.

На основе структурной декомпозиции исходная многомерная система (многоэлементная составная отражающая поверхность) сводится к совокупности взаимодействующих подсистем-панелей

, (10)

где , – векторы состояния и управляющих воздействий -й подсистемы-панели, соответственно, 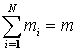; , – матрицы параметров и управлений; или – векторная функция влияния на -ю подсистему-панель со стороны всех остальных панелей.

В случае выполнения декомпозиции по управляющим входам модельное описание большой системы сводится к виду (10), если число подсистем-панелей совпадает с числом управляющих воздействий и у каждой подсистемы имеется единственный векторный управляющий вход. Однако в практике построения составных отражающих поверхностей более широкое применение нашли конструкции, когда число подсистем-панелей составного зеркала не совпадает с числом управляющих воздействий и в вектор управления -й подсистемы-панели входят компоненты управления, воздействующие на другие зеркальные щиты составной поверхности. Здесь для построения модели, полностью децентрализованной по входам, в которой число подсистем равно числу управляющих воздействий, и каждое управление прикладывается к одной подсистеме, что необходимо для решения задачи синтеза локальных регуляторов, воспользуемся следующей процедурой [5].

Представим исходную систему в виде совокупности подсистем-панелей

, (11)

в которой .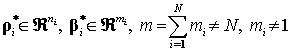

Это позволяет свести задачу декомпозиции по входам исходного крупномасштабного объекта управления – составной отражающей поверхности к задаче приведения большой системы (11) к системе вида (10), где , .

Известно [5], что при выполнении критерии управляемости для каждой из подсистем, входящих в (11)

полная децентрализация по управляющим входам может быть достигнута посредством использования преобразования Луенбергера , выполняемого путем использования квадратной матрицы , столбцами которой являются столбцы матрицы управляемости соответствующих пар системы (11)

Матрицы , , децентрализованной по входам системы находятся через одноименные матрицы , , системы (11) из соотношений

. (12)

После выполнения преобразований получаем следующее модельное представление крупномасштабного объекта – многопанельного зеркала, расчлененного по управляющим входам

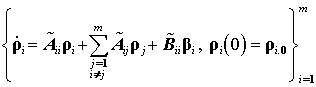. (13)

В заключение обсуждения моделей составной поверхности отметим, что при малых значениях интервальных неопределенностей в матрицах , когда , децентрализованные модельные представления (10) и (13) легко сводятся к системе с локальными параметрическими возмущениями

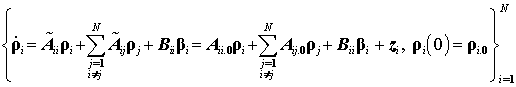, (14)

в которам , , .

Рассмотрим далее методики синтеза законов стабилизации формы многоэлементной поверхности главного зеркала радиотелескопа, находящегося под влиянием возмущений, приводящих к умеренным деформациям и смещениям зеркальных панелей, т.е. к ситуации, когда имеет место ограниченная неопределенность параметров управляемого крупномасштабного объекта.

Решение задачи робастной стабилизации будем искать как в классах централизованных, так и децентрализованных структур. Централизованное робастное управление применимо, если взаимосвязи между пластинами отражающей поверхности, особенно по управляющим цепям, отсутствуют, а это имеет место, когда пространственное положение каждой зеркальной панели регулируется независимо от других пластин. Децентрализованные методы стабилизации используются при синтезе стабилизирующих управлений для составной отражающей поверхности, у которой имеет место сильные взаимосвязи между смежными подсистемами-щитами по компонентам управляющих сигналов.

3. Централизованная робастная стабилизация положения панелей составной отражающей поверхности

3.1. Постановка задачи. В модельном описании многомерных динамических систем умеренные параметрические возмущения обычно сводят к центрированным интервальным формам с неопределенными параметрами в матрично-векторном представлении:

, (15)

где , , , , .

Централизованное управление для объекта (15) в форме линейного алгоритма стабилизации

, (16)

где – матрица обратной связи, обычно формируется при условии минимизации следующего квадратичного функционала качества [6]

, , , (17)

при этом блочно диагональные весовые матрицы и (матрицы штрафа) устанавливают разумный компромисс между стремлением наискорейшим образом ликвидировать ошибку динамической системы в фазовых координатах, колебательностью переходных процессов управления и ограничениями энергетических потерь, определенных интегралом от .

3.2. Синтез централизованного регулятора. Известно [7], что в силу малости отклонений параметров матрицы от номинального значения , систему (15) можно считать квазистационарной и ее устойчивость удается обеспечить с помощью стационарной матрицы обратной связи . Воспользовавшись известным подходом [8], выберем

. (18)

Здесь , – симметричная положительно определенная матрица, причем , которая является решением алгебраического уравнения Риккати

, (19)

где – положительное вещественное число, при этом решение уравнения (19) может быть найдено без привлечения рекуррентных процедур [8]. Для этого определим обратную матрицу

и, умножив (19) в левой и правой частях на , а затем произведя необходимые преобразования, получим линейное уравнение Ляпунова следующего вида [7]

, (20)

где – единичная матрица, алгебраические методы решения которого известны, например, из [9].

Заметим, что в соотношениях (18)…(20) матрицы и , также как и матрица , соответствуют номинальному состоянию системы.

Таким образом, закон робастного управления составной поверхностью в классе централизованных структур имеет вид

. (21)

3.3. Свойства замкнутой системы. С учетом синтезированного централизованного управления (21) динамика замкнутой параметрически возмущенной системы с робастным регулятором описывается соотношением

, (22)

при этом поведение номинальной системы при номинальных значениях матриц и характеризуется уравнением

. (23)

Отметим, что рассмотренный метод синтеза закона управления (21) обеспечивает для замкнутой номинальной системы (23) оптимальное решение в смысле квадратичного критерия качества (17), в котором .

Свойства полученной замкнутой системы (22) могут быть оценены по поведению замкнутой номинальной системы (23) с помощью следующей теоремы (которую приводим без доказательства, последнее см. в [7]):

Теорема 3.1 [7]. Пусть:

пара матриц полностью управляема;

матрица ;

степень устойчивости .

Тогда существует положительное определенное решение системы (19) и , где – собственные числа соответствующей матрицы.

Из данной теоремы следует, что замкнутая система с номинальными матрицами и асимптотически устойчива со степенью устойчивости не менее , при этом гарантируется и ее экспоненциальная устойчивость с оценкой

(24)

для любых , при этом .

Отличие возмущенной матрицы от номинальной , конечно, приводит в некоторым расхождениям между оценкой (24) и реальным поведением замкнутой системы (22). Однако возмущенное движение системы на интервале при малых деформациях отражающих пластин близко к движению стационарной системы (23), если выполняется следующее условие квазистационарности [7]:

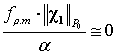или (25)

где , , – номинальная функция чувствительности с моделью

, (26)

в которой для рассматриваемого случая

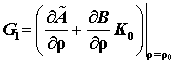. (27)

Таким образом, в квазистационарном случае система (27) имеет малые траекторную чувствительность и скорость изменения фазовых координат.

4. Децентрализованная робастная стабилизация положения панелей составной отражающей поверхности

4.1. Постановка задачи. При наличии сильных взаимосвязей между подсистемами-пластинами составной отражающей поверхности главного рефлектора высокая размерность вектора состояний приводит к заметным усложнениям процесса синтеза централизованного управления вида (21). В этом случае более удачным методом нахождения закона управления является синтез робастного регулятора в классе децентрализованных структур. Задачу синтеза децентрализованного робастного регулятора решим с использованием метода декомпозиции централизованного регулятора [6], параметры которого находятся в процессе решения глобальной задачи динамической оптимизации при структурных ограничениях с помощью классических методов аналитического конструирования регуляторов. На втором этапе матрица коэффициентов обратной связи централизованного регулятора путем использования формальных аналитических процедур приведем к блочно-диагональному виду, где каждый блок является коэффициентом обратной связи локального регулятора, обеспечивающего заданную оптимальность подсистем.

Пусть динамика составной отражающей поверхности с сильно-связными по управляющим цепям подсистемами-панелями описывается векторным дифференциальным уравнением с интервальными коэффициентами

. (28)

Представим систему (28) в виде децентрализованной по управляющим входам структуры из взаимодействующих подсистем, воспользовавшись

, (29)

в которых и .

Цель синтеза робастного управления состоит в определении децентрализованной обратной связи по фазовым координатам подсистем

, (30)

которая обеспечивает их асимптотическую устойчивость и минимум функционала

, (31)

где , .

Кроме того, значения функционала качества, вычисленные на траектории замкнутой системы, должны удовлетворять двухстороннему неравенству при всех допустимых вариациях параметров, т.е. для .

4.2. Синтез централизованного регулятора сильно-взаимосвязанной системы. Определим оптимальное управление в классе централизованных структур для системы (29), для чего задачу минимизации (31) при ограничениях (30) решим методом динамического программирования с использованием функции Ляпунова – Беллмана интервального типа.

Используя рекомендации [5], уравнение Беллмана для системы (29) представим в виде

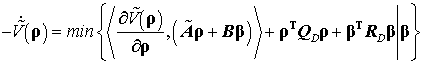, (32)

где в качестве функции Ляпунова – Беллмана возьмем интервальную квадратичную форму

. (33)

Подставив в функциональное уравнение (32) полную производную функции (33), получим

Вычислив полную производную функции по и приравняв ее к нулю, получим обобщенное управление со структурированными параметрическими возмущениями в классе централизованных структур

, (34)

в котором матрица , является решением интервального уравнения Риккати

, (35)

имеющего ту же размерность, что и исследуемая система.

4.3. Синтез децентрализованного регулятора. Синтез локального регулятора осуществим на основе декомпозиции интервального матричного уравнения (35). Для нахождения решения уравнения (35) в классе диагональных матриц в исходный функционал качества (31) введем дополнительную составляющую :

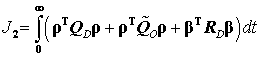, (36)

где .

Решая модифицированную задачу [10] минимизации функционала (36) при ограничениях (29) с учетом представления матрицы в виде , получаем два уравнения:

; (37)

. (38)

В силу блочно-диагональной структуры матриц , , и матрица также является блочно-диагональной, а уравнение (37) эквивалентно интервальным уравнениям

, (39)

каждое из которых соответствует -й параметрически возмущенной подсистеме (29), при этом управление принимает искомую децентрализованную форму

, (40-1)

или в более компактном представлении

, (40-2)

где – решение интервального уравнения (39), .

Заметим, что для определения блоков матрицы необходимо воспользоваться соотношениями, напрямую следующими из уравнения (39)

. (41)

4.4. Свойства локально-замкнутой системы. Уравнения взаимодействующих подсистем (29), замкнутых синтезированным децентрализованным робастным регулятором вида (40-1), имеют вид

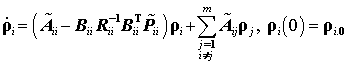, (42-1)

или в более компактной форме записи

. (42-2)

Данная замкнутая крупномасштабная система асимптотически устойчива при условии, когда ограниченные параметрические возмущения удовлетворяют соотношениям

, (43)

, (44)

в которых – положительно определенные решения уравнений Риккати

соответственно.

Это вытекает из следующей теоремы, которую приведем без доказательства (доказательство см. в [5])

Теорема 4.1 [5]. Пусть для системы (28) или (29) и для :

пары матриц полностью управляема;

пары матриц наблюдаемы

существует интервальная функция Ляпунова с бесконечно малым верхним пределом и справедливо неравенство:

, (45)

где – верхняя граница максимального собственного числа интервальной матрицы

Тогда децентрализованное управление (40) обеспечивает асимптотическую устойчивость замкнутой системы (42).

Известно [5], что при выполнении условий данной теоремы для каждой изолированной подсистемы вида (29) существует интервальная функция Ляпунова вида

которая в целом для всех взаимодействующих параметрически возмущенных подсистем (29) многомерной системы (28) есть

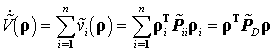. (46)

Полная производная функции (46), построенная вдоль траекторий подсистем (29), замкнутых синтезированным локальным управлением (40), с учетом выражений (37), (38), (41) и равная

(47)

является отрицательно определенной функцией, т.е. , откуда и следует, что условие асимптотической устойчивости (45) выполнено и замкнутая система (42) асимптотически устойчива при всех вариациях параметров многомерного объекта управления, ограниченных условиями (43)-(44).

5.Выводы

Сформированы модельные описания активной многоэлементной составной поверхности главного зеркала радиотелескопа, находящейся под воздействием гравитационных, термических и ветровых возмущений, как крупномасштабной интервальной системы с параметрическими возмущениями. Рассмотрены модели исследуемого многомерного объекта при отсутствии и при наличии межэлементных связей. В классе централизованных и децентрализованных структур синтезированы робастные законы стабилизации пространственного состояния параметрически возмущенных отражающих щитов составного главного зеркала радиотелескопа, обеспечивающие асимптотическую устойчивость замкнутым многомерным объектам управления.

Литература

1. Orfei A., Morsiani M., Zacchiroli G., etc. The Active Surface System on the Noto Radio Telescope.//the 6th European VLBI Network Symposium, June 25th-28th 2002, Bonn, Germany – P.13-16.

2. Lacasse R.J. The Green Bank Telescope Active Surface System.//National Radio Astronomy Observatory (NRAO).//Technical Report 184, GBT Memo Series, 1998.

3. Коровьяков А.Н., Сударчиков С.А., Ушаков А.В. Следящий оптоэлектронный мониторинг деформаций в задаче динамической юстировки устройств пространственного наблюдения/Под ред. А.В. Ушакова. – СПб.: СПбГУ ИТМО, 2008.– 132c.

4. Меньшиков Г.Г. Интервиализация приближенных формул. Численное суммирование рядов //Интервальный анализ и методы вычислений. – СПб.: Изд-во СПбгу, 1996. – 42с.

5. Шашихин В.Н. Интервальные динамические системы: Модели, анализ, синтез. – СПб.: Изд-во СПбГПУ, 2003. – 214с.

6. Шашихин В.Н. Теория управления: Модели, анализ и синтез крупномасштабных динамических систем. – СПб.: Изд-во СПбГТУ, 1999. – 116с.

7. Дроздов В.Н., Мирошник И.В., Скорубский В.И. Системы управления с микро-ЭВМ. – Л.: Машиностроение. Ленингр. отд-ние, 1989. – 284с.

8. Фурасов В.Д. Устойчивость движения, оценки, стабилизация. – М.: Наука, 1977. – 247с.

9. Икрамов Х.Д. Численное решение матричных уравнений. – М.: Наука, 1984. – 192с.

10. Шашихин В.Н. Декомпозиция динамических систем с использованием инверсной процедуры оптимизации.//Автоматика, 1991, № 1. С.45-52.