ЧИСЛЕННЫЙ АНАЛИЗ МИКРОПОЛОСКОВЫХ ПЕЧАТНЫХ АНТЕНН

 

К. Б. Папилов
ОАО «МКБ «Компас»

Получена 18 апреля 2011 г.

 

Аннотация. Проведено сопоставление экспериментальных данных, полученных при измерении характеристик печатных антенн, с результатами компьютерного моделирования тех же типов печатных антенн. Оценена сходимость результатов в зависимости от точности построения модели и выбора граничных условий. Показано соотношение между точностью и временем решения.

Ключевые слова: печатные антенны, численное моделирование.

Abstract. We have compared experimental data, obtained from measuring characteristics of the patch antennae, with the results of computer modeling of the same type of patch antennae. We have also evaluated the resulting convergence depending on the accuracy of the model and boundary conditions selection. Finally, we have presented a correlation between the accuracy and computing time.

Keywords: patch antennas, computer modeling.

 

1. Постановка задачи

В связи с резким ростом производительности современных персональных компьютеров широкое распространение в практике инженерного проектирования получают программы электродинамического моделирования СВЧ структур. Наиболее популярными системами такого типа являются: HFSS, CST Microwave Studio, FEKO, а также ряд других. Данные программы являются эффективным инструментом решения практических задач разработки различных СВЧ устройств и систем. Они отличаются друг от друга методами решения граничных задач электродинамики, интерфейсами и некоторыми дополнительными возможностями. Например, программа Microwave Studio основана на методе конечных разностей во временной области (FDTD), а программа FEKO -  комбинирует метод моментов, физическую оптику и геометрическую теорию дифракции. Поэтому разработчик может выбирать тот или иной подход решения задачи наиболее адекватный конкретным требованиям технического задания.

Важной проблемой использования современных систем электродинамического моделирования является проблема достоверности получаемых численных результатов. Ее актуальность обусловлена, в том числе и тем, что обсуждаемые системы являются сложным объектом, требующим для правильного функционирования установки многочисленных параметров решения граничной задачи, которые не производятся автоматически, а определяются пользователем программы.  Естественно использовать в качестве критерия достоверности сравнение расчетных данных с экспериментальными результатами.

В данной работе исследуются особенности применения программы CST Microwave Studio для расчета широко используемых микрополосковых антенн. Они получили распространение еще в 50-х годах прошлого века и являются одним из наиболее хорошо изученных типов антенн. Система CST Microwave Studio является популярным программным продуктом. Поэтому представляет интерес анализ особенностей его использования для расчета и проектирования интересных с практической точки зрения антенн. Чтобы выяснить, можно ли полагаться на расчеты, полученные при помощи CST Microwave Studio было решено в соответствии со сформулированным выше критерием достоверности провести сравнение экспериментальных результатов с расчетными.

 

2. Моделирование ПА с учетом элементов реальной конструкции

В качестве объекта исследования была выбрана полуволновая микрополосковая антенна. Экспериментальная модель представляет собой печатную антенну, выполненную на фольгированном диэлектрике ФЛАН-10 толщиной 8 мм.

Рис. 1. ПА на металлическом диске.

 

Антенна имеет форму квадрата со стороной 45 мм. В качестве подстилающей поверхности был выбран диск фольгированного текстолита диаметром 300 мм (см. рис. 1.).

Верхний проводник ПА имеет форму квадрата с зубцами. Данные зубцы используются для удобства настройки. Отрезая эти зубцы можно сдвигать резонансную частоту вверх. Для более точного сравнения будет лучше провести серию экспериментов, отрезая постепенно зубцы от антенны. Для простоты сравнения антенны возбуждаются в одной точке, причем лежащей вдоль оси х или у, чтобы возбудить только одно колебание. Соответственно и зубцы отрезаются вдоль сторон, отвечающих за резонансную частоту возбуждаемого колебания.

Эксперименты проведены следующие:

1)     Антенна со всеми зубцами (см. рис. 2).

Рис.2. Макет ПА со всем зубцами.

 

Измеренная зависимость КСВ от частоты приведена на рис. 3.

 

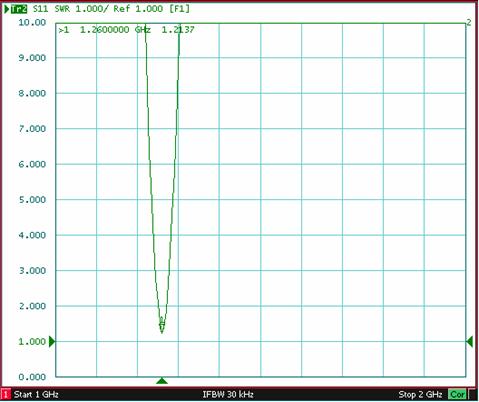
Рис.3. Измеренная зависимость КСВ от частоты для ПА со всеми зубцами.

 

Модель этой антенны, построенная и рассчитанная в CST Microwave Studio показана на рис. 4.

 

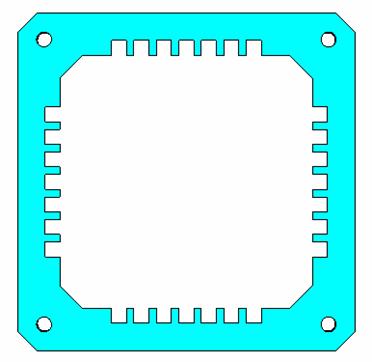
Рис.4. Модель ПА со всеми зубцами.

 

Результаты моделирования показаны на рис. 5.

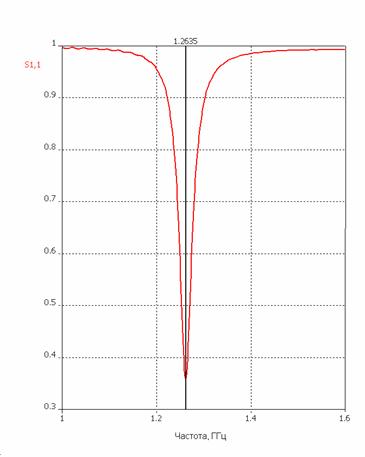
Рис. 5. Расчетная частотная характеристика ПА со всеми зубцами.

 

Во втором опыте от экспериментальной модели отрезаются по одному зубцу с двух противоположных сторон, и соответствующие изменения вносятся в компьютерную модель. В третьем опыте отрезаются еще 4 зубца с каждой стороны и затем, в четвертом -  все зубцы. Следует сравнить между собой резонансные частоты компьютерных и экспериментальных моделей.

Сопоставим графически экспериментальные и расчетные результаты. На графике (рис. 6) нанесены две линии, одна из которых это экспериментальная зависимость центральной частоты ПА от номера эксперимента, а вторая – расчетная.

 

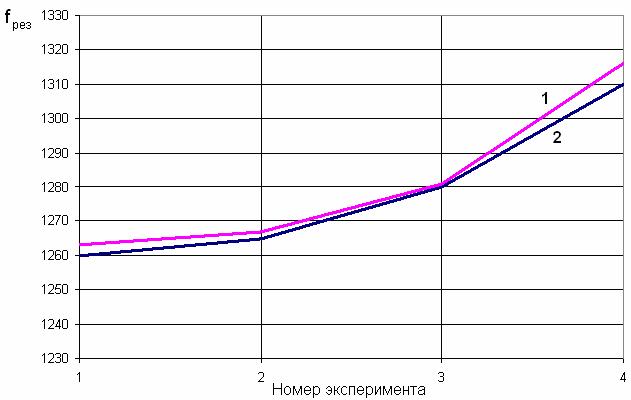
Рис. 6. Сравнение экспериментальных и расчетных значений резонансных частот.

 

         Из графика, приведенного на рис. 6 видно, что расчетные значения резонансных частот отличаются от измеренных на единицы мегагерц. По отношению к абсолютному значению резонансной частоты порядка 1300 МГц эта разница составляет доли процента, что можно считать приемлемым результатом с точки зрения использования расчетных данных для проектирования антенн данного типа.

Также, важным является вопрос достоверности вычисления диаграммы направленности рассчитываемых антенн. Для этого сравнивались между собой рассчитанная ДН и измеренная. В качестве исследуемого образца была выбрана классическая ПА с воздушным заполнением (рис. 7).

Рис. 7. ПА с воздушным заполнением.

 

Данная ПА отличается от рассматриваемой выше модели ПА на ФЛАНе более узкой ДН, что позволит нагляднее сопоставить расчетную и экспериментальную ДН. На рис. 8 нанесены две сопоставляемые ДН, измеряемые в плоскости угла θ, при φ = 90°. Кривая под номером 1 представляет результаты компьютерного моделирования антенны, а кривая 2 – экспериментально измеренную ДН.  Из графика видно, что в направлении основного лепестка ДН практически идентичны, а расхождения имеются при углах θ > 100°.  Это объясняется тем, что при данных углах уровень сигнала сопоставим с уровнями отраженных сигналов, присутствующих при измерении антенны в неидеальных условиях.

 

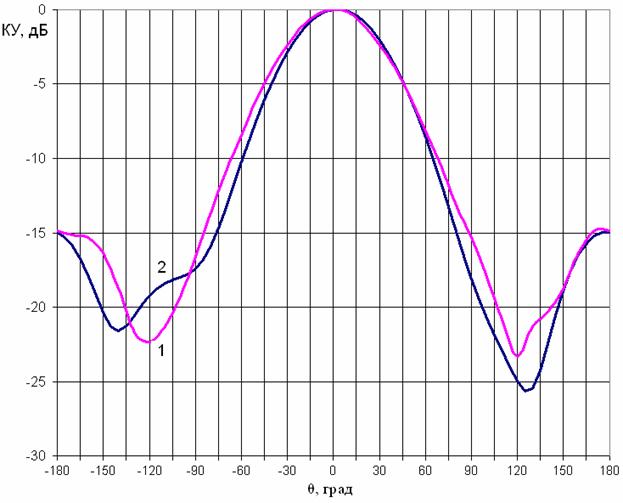
Рис. 8. Сопоставление диаграмм направленности.

 

Важным вопросом, возникающим при моделировании ПА является влияние размеров экрана, на котором она располагается на параметры антенны. Интересно также найти размеры экрана, при которых он перестает влиять на параметры ПА и ее можно анализировать в рамках модели с бесконечным металлическим экраном. Переход к такой модели весьма выгоден с точки зрения уменьшения времени анализа ПА, поскольку объем, в котором ищется электромагнитное поле в модели с бесконечным экраном намного меньше объема в модели с экраном конечных размеров.

Было произведено моделирование трех ПА с подстилающими поверхностями разных размеров. В первом случае это был квадрат со стороной 100 мм, во втором – 200 мм, а в третьем – 300 мм. И четвертый - ПА на бесконечной подстилающей поверхности. Изменения параметров  - резонансной частоты и полосы пропускания – показаны на рис. 9 и 10, соответственно.

 

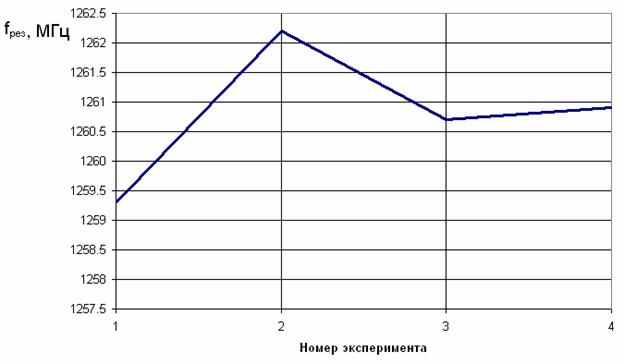
Рис. 9. Влияние размера подстилающей поверхности на резонансную частоту ПА.

 

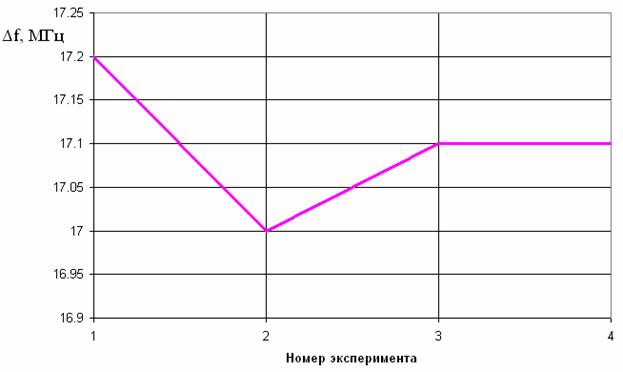
Рис. 10. Влияние размера подстилающей поверхности на ширину полосы пропускания ПА.

 

         Из рис. 9 и 10 видно, что, начиная с экрана размером 300 мм влияние на резонансную частоту и полосу пропускания практически незаметно и указанные параметры совпадают с расчетными данными, полученными с помощью модели с бесконечным экраном. Сильнее всего результаты с отличаются от предельного случая (бесконечный экран) при размере подстилающей поверхности 100 мм. Это объясняется тем, что ее размеры близки к половине длины волны, которая равна 188 мм. При этом токи на металлическом экране резонируют и их влияние возрастает. Из представленных выше результатов можно сделать вывод о том, что модель с бесконечным экраном, использованная для построения кривых на рис. 6 вполне оправданна, так как экспериментальный образец имел экран с диаметром равным 300 мм. Отметим, что при небольших размерах подстилающей поверхности заменять ее бесконечной электрической стенкой некорректно.

 

3. Влияние параметров численного решения на результаты расчетов

Как известно, в программах электродинамического моделирования исследуемый объект описывается граничными условиями на его поверхностях. В CST Microwave Studio они бывают нескольких типов: граничные условия на магнитной и электрической стенках, условия излучения, периодические граничные условия, импедансные граничные условия, имитирующие проводник с потерями и ряд других. Наибольший интерес для нас представляют условия излучения. При анализе излучающих структур соответствующие им поверхности излучения ограничивают общий объем, в котором ищется электромагнитное поле. Через эти поверхности энергия поля должна проходить без возмущения. Следует отметить, что не всякое поле удовлетворяет граничным условиям излучения, которые носят приближенный характер. Полностью им удовлетворяет только поле излучения или поле в дальней зоне. Реальное поле, кроме поля излучения, содержит, так называемое ближнее поле, которое убывает при удалении от источника излучения быстрее, чем дальнее поле. Оно не удовлетворяет условиям излучения. Поэтому поверхности излучения должны устанавливаться на расстоянии от антенны, на котором ближнее поле пренебрежимо мало. Структура ближнего поля зависит от конструкции излучателя. Поэтому ответить на вопрос о минимальном расстоянии от антенны до поверхности излучения можно лишь, анализируя результаты численного решения электродинамической задачи.

При моделировании ПА область, в которой решалась электродинамическая задача имела форму параллелепипеда со следующими границами: сверху и по бокам поверхности излучения, снизу эквивалент электрической стенки, на которой располагалась модель ПА. Так как открытые границы лишь эквивалент свободного пространства, то стоит убедиться, насколько он приближен к реальности. Для этого рассчитывались три модели с разными расстояниями от структуры до поверхностей излучения. В первом случае указанное расстояние равно λ/8, во втором - λ/4 а в третьем - λ/2. В качестве критерия выберем резонансную частоту исследуемой модели и ее полосу пропускания по уровню 0,5. На рис. 11 показаны значения резонансных частот ПА в зависимости от номера эксперимента, а на рис. 12 зависимость ширины полосы пропускания от того же параметра.

 

 

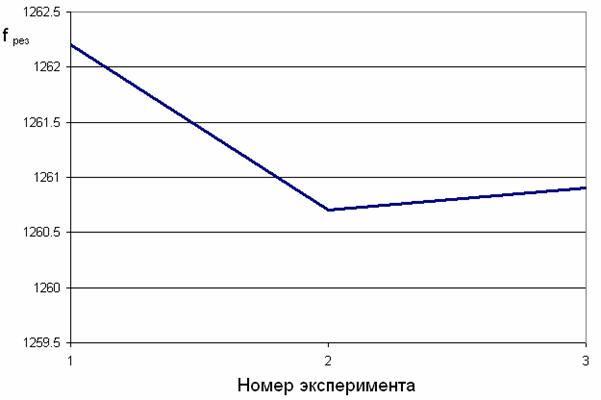
Рис. 11. Влияние расстояния от структуры до границ излучения на резонансную частоту ПА.

 

 

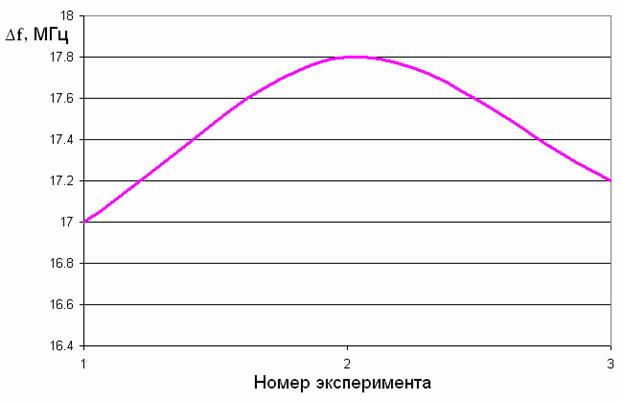
Рис. 12. Влияние расстояния от структуры до границ излучения на ширину полосы пропускания ПА.

 

         Как видно из графиков, в обоих случаях погрешность параметров составляет десятые доли мегагерц, что позволяет использовать наименьшее расстояние до границ излучения для сокращения времени решения задачи.

Важным параметром решения граничной задачи является скорость его сходимости, а также связь точности решения с размерами ячеек, на которые разбивается пространство, в котором ищется решение.  В CST Microwave Studio размеры ячеек и их число определяются адаптивным путем. Решение проводится в несколько этапов. На каждом последующем шаге размеры ячеек уменьшаются, а их общее число увеличивается. Поэтому номер шага адаптации сетки может служить параметром, описывающим размеры ячеек и их число.

На рис. 13 изображена зависимость числа ячеек в модели ПА от номера шага адаптации.  На рис. 14 изображены частотные характеристики, полученные на разных шагах. Номер кривой указанный на графике соответствует номеру шага адаптации.

 

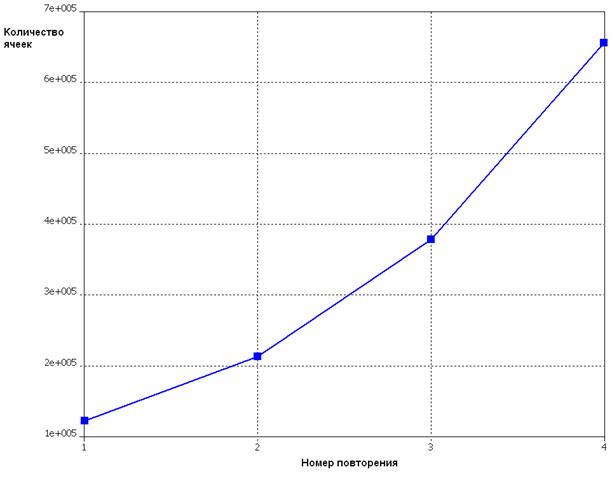
Рис. 13. Зависимость числа ячеек от номера повторения.

 

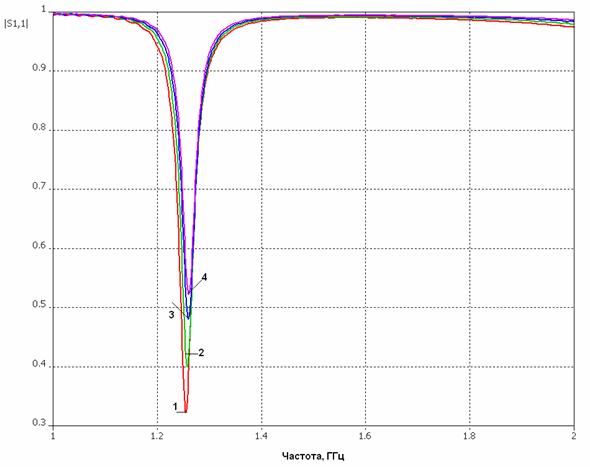
Рис. 14. Влияние частоты разбиения сетки на результат расчета.

 

         Из рис. 14 видно, что разброс значений резонансной частоты составляет единицы мегагерц, а согласование и соответственно значения входных сопротивлений несколько различаются. Как видно из рис. 13 с каждым новым разбиением модели на ячейки увеличивается их число, что увеличивает время решения. Рассмотрим, как растет время решения в зависимости от номера шага. На рис. 15 показана указанная зависимость. Видно, что время, как и количество ячеек, растут экспоненциально. Для данной модели к четвертому проходу число ячеек, на которые разбивается модель, равно приблизительно шестистам тысячам. При таком количестве ячеек среднестатистическая ЭВМ решает данную задачу приблизительно за 14 тысяч секунд или почти 4 часа. Поэтому при выборе количества повторений стоит соотносить точность вычисления и длительность времени решения.  Например, в данной ситуации для расчета резонансной частоты и диаграммы направленности можно ограничиться 2-3 повторениями, а если требуется получить точные значения входных сопротивлений, то число повторений следует увеличить до требуемой сходимости результатов.

 

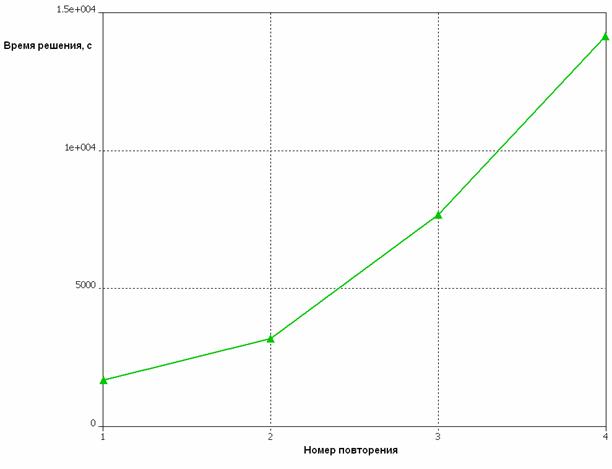
Рис. 15. Зависимость времени решения от номера повторения.

 

4. Заключение

Из данной статьи следует, что программы электродинамического моделирования являются довольно точным инструментом моделирования микрополосковых ПА. Они позволяют хорошо прогнозировать параметры ПА с учетом присутствия в ее составе реальных конструктивных элементов, таких как подстроечные элементы и экран конечных размеров. Важное значение имеют выбор места расположения поверхностей излучения, а также формулировка критерия сходимости процесса адаптации сетки разбиения пространства. Основным недостатком электродинамических моделей рассмотренного типа является достаточно большое время, необходимое для получения корректного численного результата. Фактор затрат компьютерного времени становится особенно существенным, когда речь идет о расчете более сложных структур, нежели та, что рассмотрена в данной работе, например решеток микрополосковых излучателей.