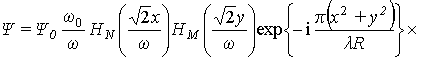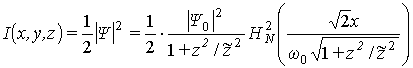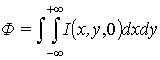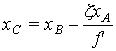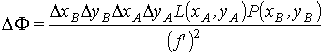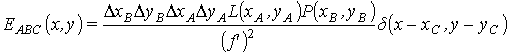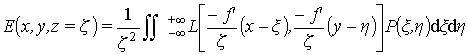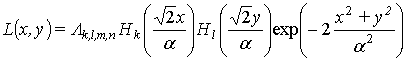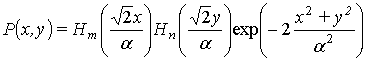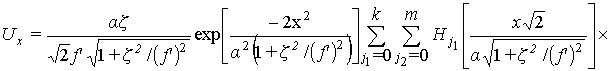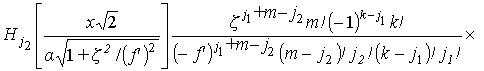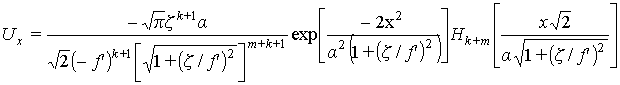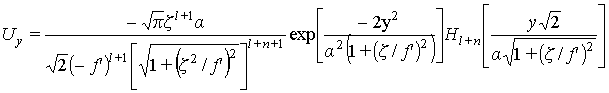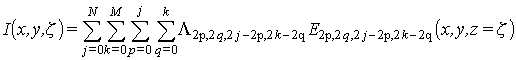Геометрооптическая модель прохождения моды эрмито-гауссового пучка через оптическую систему
Р. Е.
Ильинский,
независимый исследователь
Получена 20 марта 2013 г.
Аннотация. Для моделирования прохождения через оптическую систему моды эрмито-гауссового пучка предлагается заменить эрмито-гауссов пучок на набор базовых излучающих систем. Каждая базовая излучающая система состоит из тонкой линзы, излучающей площадки и амплитудного фильтра в плоскости линзы. Последовательность базовых излучающих систем создает в каждой точке пространства плотность потока энергии излучения, которая прямо пропорциональна квадрату модуля амплитуды моды эрмито-гауссового пучка. В качестве примера рассмотрено моделирование прохождение моды эрмито-гауссового пучка через одиночную линзу.
Ключевые слова: построение траектории луча, эрмито-гауссов пучок.
Abstract. For modeling of the transmissions through the optical system modes Hermite-Gaussian beam is proposed to replace the Hermite-Gaussian beam on a set of basic radiating systems. Each base radiating system consists of a thin lens, emitting area and amplitude filter in the plane of the lens. The sequence of base radiating systems creates at each point of the flux density of the radiation energy, which is directly proportional to the square of the modulus of the amplitude modes Hermite-Gaussian beam. As an example, the simulation of the transmission modes Hermite-Gaussian beam through a single lens is considered.
Keywords: Ray tracing,
Hermite-Gaussian beam.
Достаточно часто лазерное излучение, собственные типы колебаний (моды) открытых резонаторов и оптических волноводов представляет собой узкие пучки, поперечные размеры которых намного больше длины волны, а амплитуда медленно изменяется в продольном направлении. При этом электромагнитное излучение сконцентрировано около одной линии (оси пучка) и быстро спадает до нуля в поперечных направлениях. Общепризнано [4,5], что наиболее просто и достаточно полно электромагнитное излучение с подобным пространственным распределением энергии описывают эрмито-гауссовы пучки. Для моделирования прохождения эрмито-гауссовых пучков через оптические системы предложен целый ряд методов [6,4,7,8]. Предлагаемый в настоящей статье метод является логическим продолжением более ранних работ автора [2,3], где задача о прохождении гауссовых пучков через оптическую систему была сведена к решению стандартной задачи геометрической оптики - расчету хода лучей через оптическую систему. Преимущества и недостатки геометрооптических моделей изложены в статье [12] на примере дифракции плоской волны на полуплоскости.
Если в декартовой системе координат OXYZ плоскоть OXY является плоскостью перетяжки, а ось OZ совпадает с осью моды TEMN,M эрмито-гауссового пучка, то комплексная амплитуда моды TEMN,M описывается выражением [4,6,5]:
 , (1)
, (1)
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() – конфокальный параметр гауссового пучка, l - длина волны излучения, Y0 -начальное значение амплитуды; w0- параметр, характеризующий размеры пятна в плоскости
OXY, Hl (.) - полином Эрмита [1]:
– конфокальный параметр гауссового пучка, l - длина волны излучения, Y0 -начальное значение амплитуды; w0- параметр, характеризующий размеры пятна в плоскости
OXY, Hl (.) - полином Эрмита [1]:
H0(x)=1, H1(x)=2x, H2(x)=4x2−2,…
Квадрат модуля амплитуды моды TEMN,M эрмито-гауссового пучка равен:
 . (2)
. (2)
Для моды TEMN,M эрмито-гауссового пучка мощность равна:
При подстановке в формулу (3) выражения (2) и, учитывая свойство ортогональности полиномов Эрмита, получим:
Базовая
излучающая система
состоит из тонкой линзы O, в передней
фокальной плоскости которой расположен источник излучения (рис. 1), а в
плоскости линзы расположен амплитудный фильтр. Линза O и источник излучения находятся в среде с показателем
преломления равным единице. Фокусное расстояние линзы равно f '. Обозначим переднюю фокальную плоскость объектива O как плоскость ![]() , а плоскость, в которой находится линза O, как
плоскость
, а плоскость, в которой находится линза O, как
плоскость ![]() . Введем систему координат OXYZ. Ось OZ
совпадает с оптической осью объектива O; плоскость OXY совпадает
с плоскостью
. Введем систему координат OXYZ. Ось OZ
совпадает с оптической осью объектива O; плоскость OXY совпадает
с плоскостью ![]() .
.

Рисунок 1: Базовая излучающая система.
Рассмотрим луч ABC, который исходит из точки A в
плоскости ![]() и пересекает плоскость
и пересекает плоскость ![]() в точке B.
После прохождения объектива этот луч пересекает плоскость z=ζ в
точке C(xC,yC,zC=ζ). Далее будем считать, что прохождение луча через объектив O
описывается законами параксиальной
оптики. В этом случае координаты точки C равны [9]:
в точке B.
После прохождения объектива этот луч пересекает плоскость z=ζ в
точке C(xC,yC,zC=ζ). Далее будем считать, что прохождение луча через объектив O
описывается законами параксиальной
оптики. В этом случае координаты точки C равны [9]:
где xA, yA - абсцисса и ордината точки A, xB, yB - абсцисса и ордината точки B.
Рассмотрим лучевую трубку
ABC. Эту трубку заполняют лучи, которые пересекает плоскость ![]() в пределах прямоугольной площадки
□A (|x−xA|≤ DxA/2, |y−yA|≤ DyA/2), а плоскость
в пределах прямоугольной площадки
□A (|x−xA|≤ DxA/2, |y−yA|≤ DyA/2), а плоскость ![]() в пределах площадки □B (|x−xB|≤ DxB/2, |y−yB|≤ DyB/2. Пусть ΔxB→0, ΔyB→0, ΔxA→0, ΔyA→0. Представим мощность ΔΦ,
в участке BC лучевой трубки в виде:
в пределах площадки □B (|x−xB|≤ DxB/2, |y−yB|≤ DyB/2. Пусть ΔxB→0, ΔyB→0, ΔxA→0, ΔyA→0. Представим мощность ΔΦ,
в участке BC лучевой трубки в виде:
ΔΦ=L(A,B)×[DxBDyBDxADyAP(A,B)], (6)
где P (A,B) - коэффициент пропускания амплитудного
фильтра в плоскости ![]() для луча AB.
L(A,B) - коэффициент пропорциональности. Далее
будем считать, что коэффициент пропускания амплитудного фильтра зависит только
от координат точки B: P(A,B)=P(xB,yB), аналогично примем, что коэффициент
пропорциональности L(A,B) зависит только от координат точки A L (A,B)=L(xA,yA)/(f')2 .Тогда формула (6)
примет вид:
для луча AB.
L(A,B) - коэффициент пропорциональности. Далее
будем считать, что коэффициент пропускания амплитудного фильтра зависит только
от координат точки B: P(A,B)=P(xB,yB), аналогично примем, что коэффициент
пропорциональности L(A,B) зависит только от координат точки A L (A,B)=L(xA,yA)/(f')2 .Тогда формула (6)
примет вид:
Плотность потока энергии в плоскости z=z, которая обусловлена мощностью DF, в участке BC лучевой трубки, описывается выражением [10]:
где xC, yC - координаты точки C [см. формулы (5)]; d(x,y) - двумерная дельта-функция Дирака.
Проинтегрировав выражение (8) по плоскости ![]() и плоскости
и плоскости ![]() , получим плотность потока энергии E(x,y)
в плоскости z=z:
, получим плотность потока энергии E(x,y)
в плоскости z=z:
Далее будем считать, что функции L(x,y) и P(x,y) описываются выражениями:
где Lk,l,m,n, a - постоянные коэффициенты. После подстановки формул (10),(11) в выражение (9) получим
где
 , (13)
, (13)
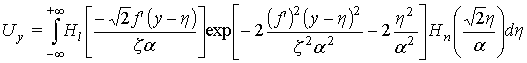 . (14)
. (14)
Введем новую переменную
 . (15)
. (15)
В результате подстановки переменной v и использования теоремы сложения полиномов Эрмита [1] интеграл (13) примет вид:
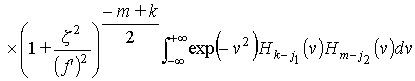 . (16)
. (16)
C учетом ортогональности полиномов Эрмита выражение (16) может быть преобразовано к виду
Аналогично доказывается
После подстановки выражений (17), (18) в формулу (12) получим, что базовая излучающая система создает в плоскости z=z плотность потока энергии
где
Необходимо отметить, что функции (10), (11), (19) могут принимать отрицательные значения. Следовательно, базовая излучающая система к виртуальным объектам, которые не могут существовать в материальном мире. Однако отрицательные значения яркости, освещенности и т. д. используются в теоретической фотометрии в качестве промежуточных величин [11] при расчетах.
В соответствии с формулой (2) интенсивность одиночной моды TEMN,M эрмито-гауссова пучка в плоскости z=z может быть представлена в виде суммы ряда:
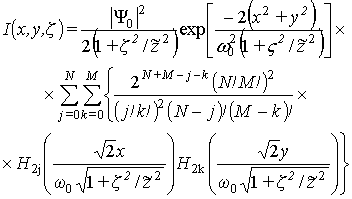 .
(21)
.
(21)
Если в функцию (20) подставить a=w0, ![]() , то ряд (21) может быть записан как:
, то ряд (21) может быть записан как:
 .
(22)
.
(22)
Формула бинома Ньютона позволяет представить сомножитель в прямоугольных скобках из формулы (22) в виде:
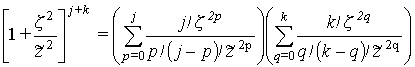 . (23)
. (23)
После подстановки формулы (23) в выражение (22) получим
 . (24)
. (24)
Согласно формуле (19) выражение (24) можно рассматривать как сумму плотностей потоков энергии, создаваемых базовыми излучающими системами:
при условии, что в формулах (10), (11),
(20), (19) выполняются равенства a=w0, ![]() ,
,
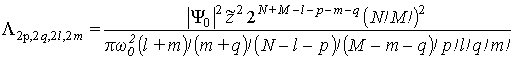
Пусть на расстоянии 2000 мм от перетяжки
моды TEM1,2
эрмито-гауссова пучка находится вершина первой поверхности линзы (рис. 2).
Основные параметры моды TEM1,2 Эрмито-Гауссова пучка: w0=0.05 мм, l=0.532 мкм, ![]() =14.7631 мм, F=0.1
Вт. Эти значения и формула (4) позволяют найти квадрат модуля начального
значения амплитуды: |Y0|2=3.1831 Вт/мм2. Оптическая ось линзы совпадает с
осью пучка. Первая поверхность линзы является выпуклой сферической. Ее радиус
равен 51.5 мм. Вторая поверхность линзы плоская. Толщина линзы по оси
составляет 6.5 мм. Линза находится в среде с показателем преломления 1.
Показатель преломления материала линзы для длины волны излучения равен 1.515.
Плоскость анализа (плоскость
=14.7631 мм, F=0.1
Вт. Эти значения и формула (4) позволяют найти квадрат модуля начального
значения амплитуды: |Y0|2=3.1831 Вт/мм2. Оптическая ось линзы совпадает с
осью пучка. Первая поверхность линзы является выпуклой сферической. Ее радиус
равен 51.5 мм. Вторая поверхность линзы плоская. Толщина линзы по оси
составляет 6.5 мм. Линза находится в среде с показателем преломления 1.
Показатель преломления материала линзы для длины волны излучения равен 1.515.
Плоскость анализа (плоскость ![]() ) находится на расстоянии 102 мм от второй поверхности линзы.
) находится на расстоянии 102 мм от второй поверхности линзы.
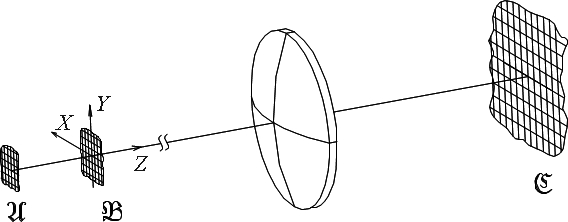
Рисунок 2: К расчету прохождения излучения через линзу.
Заменим моду эрмито-гауссова пучка набором базовых излучающих систем. Плоскости ![]() всех базовых излучающих систем
совпадают с плоскостью перетяжки пучка, оптические оси линз этих систем также
совпадают с осью пучка. При этом будут также совпадать плоскости
всех базовых излучающих систем
совпадают с плоскостью перетяжки пучка, оптические оси линз этих систем также
совпадают с осью пучка. При этом будут также совпадать плоскости ![]() всех базовых излучающих систем.
Отличаются базовые излучающие системы друг от друга только видом функций L(x,y)
и P(x,y) в плоскостях
всех базовых излучающих систем.
Отличаются базовые излучающие системы друг от друга только видом функций L(x,y)
и P(x,y) в плоскостях ![]() и
и ![]() соответственно.
соответственно.
Разделим плоскость ![]() на сеть из
на сеть из ![]() ×
×![]() прямоугольных ячеек; плоскость
прямоугольных ячеек; плоскость ![]() разделим на сеть из
разделим на сеть из ![]() ×
×![]() прямоугольных ячеек; плоскость
прямоугольных ячеек; плоскость ![]() разделим на сеть из
разделим на сеть из ![]() ×
×![]() прямоугольных ячеек. Сопоставим
каждому лучу, задаваемого координатами x=ξA, y=ηA
центра центра ячейки в плоскости
прямоугольных ячеек. Сопоставим
каждому лучу, задаваемого координатами x=ξA, y=ηA
центра центра ячейки в плоскости ![]() и координатами x=ξB, y=ηB
центра ячейки в плоскости
и координатами x=ξB, y=ηB
центра ячейки в плоскости ![]() , мощность DFS(ξA,ηA,ξB,ηB).
Мощность, которая исходит с ячейки в плоскости
, мощность DFS(ξA,ηA,ξB,ηB).
Мощность, которая исходит с ячейки в плоскости ![]() и проходит через ячейку в плоскости
и проходит через ячейку в плоскости ![]() , для одиночной базовой излучающей
системы может быть аппроксимирована значением [см. формулы (7), (10), (11)]
, для одиночной базовой излучающей
системы может быть аппроксимирована значением [см. формулы (7), (10), (11)]
![]()
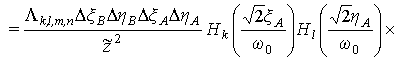
 , (26)
, (26)
где DxA, DhA, DxB, DhB размеры прямоугольных ячеек в
плоскости ![]() и в плоскости
и в плоскости ![]() соответственно. Так как геометро-оптический аналог
моды эрмито-гауссова пучка состоит из набора базовых излучающих систем, то, по
аналогии с формулой (25), мощность излучения, который исходит с ячейки в
плоскости
соответственно. Так как геометро-оптический аналог
моды эрмито-гауссова пучка состоит из набора базовых излучающих систем, то, по
аналогии с формулой (25), мощность излучения, который исходит с ячейки в
плоскости ![]() и проходит через ячейку в плоскости
и проходит через ячейку в плоскости ![]() , равна
, равна
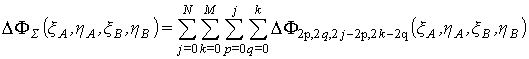 . (27)
. (27)
Центр каждой ячейки в
плоскости ![]() соединим лучами со всеми центрами
ячеек в плоскости
соединим лучами со всеми центрами
ячеек в плоскости ![]() . Выполним расчет полученного пучка лучей от плоскости
. Выполним расчет полученного пучка лучей от плоскости ![]() до плоскости
до плоскости ![]() через линзу O базовой излучающей системы и выпукло-плоскую линзу. Расчет
лучей от плоскости
через линзу O базовой излучающей системы и выпукло-плоскую линзу. Расчет
лучей от плоскости ![]() через линзу O базовой
излучающей системы должен выполняться по формулам параксиальной оптики. Расчет
лучей через выпукло-плоскую линзу может быть выполнен как в параксиальном
приближении, так и по точным формулам. Поток излучения DFC, падающий на ячейку в плоскости
через линзу O базовой
излучающей системы должен выполняться по формулам параксиальной оптики. Расчет
лучей через выпукло-плоскую линзу может быть выполнен как в параксиальном
приближении, так и по точным формулам. Поток излучения DFC, падающий на ячейку в плоскости ![]() , равен
, равен
DFC=SDFS(ξA,ηA,ξB,ηB), (28)
где суммирование ведется по всем лучам, которые попадают в данную
ячейку. По мощности, падающей на ячейку в плоскости ![]() , находится среднее значение плотность
потока энергии в ячейке. Средние значения плотности потока энергии,
соотнесенные с центрами ячеек, аппроксимируют значения плотности потока энергии
в плоскости
, находится среднее значение плотность
потока энергии в ячейке. Средние значения плотности потока энергии,
соотнесенные с центрами ячеек, аппроксимируют значения плотности потока энергии
в плоскости ![]() .
.
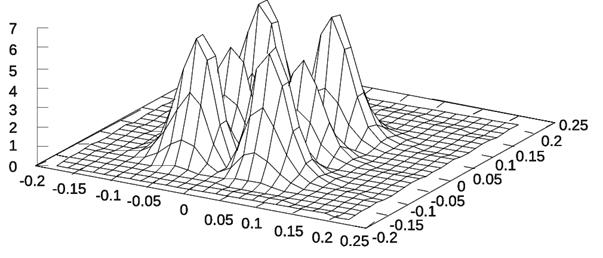
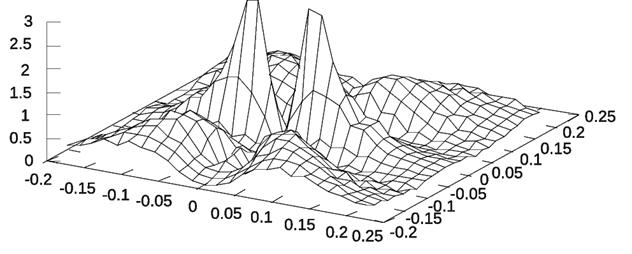
На рис. 3,a и 4,a показаны результаты
расчетов, выполненных при ![]() =64,
=64, ![]() =128, ΔξA=ΔhA=0.003125, ΔξB=ΔhB=0.0015625. На рисунках 3.b и 4.b
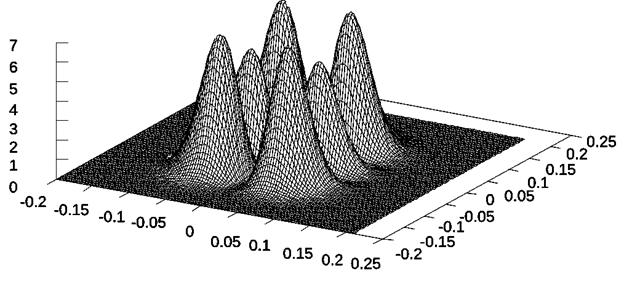
показаны результаты расчетов, которые выполнены для тех же самых исходных
данных по программе Fresnel 4.1 Pro. Основные алгоритмы программы Fresnel 4.1
Pro описаны в работах [7,8].
=128, ΔξA=ΔhA=0.003125, ΔξB=ΔhB=0.0015625. На рисунках 3.b и 4.b
показаны результаты расчетов, которые выполнены для тех же самых исходных
данных по программе Fresnel 4.1 Pro. Основные алгоритмы программы Fresnel 4.1
Pro описаны в работах [7,8].
a)
b)
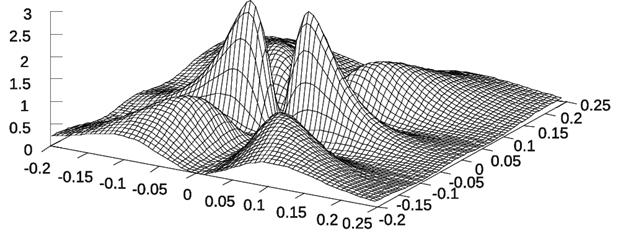
Рисунок 3:
Плотность потока энергии
в плоскости ![]() . a) Геометрооптическая модель, расчет хода лучей через линзу
выполнен в параксиальном приближении. b)Расчет по программе Fresnel 4.1 Pro,
параксиальное приближение прохождения излучения через линзу.
. a) Геометрооптическая модель, расчет хода лучей через линзу
выполнен в параксиальном приближении. b)Расчет по программе Fresnel 4.1 Pro,
параксиальное приближение прохождения излучения через линзу.
a)
b)
Рисунок 4:
Плотность потока энергии
в плоскости ![]() . a) Геометрооптическая модель, расчет хода лучей через линзу
выполнен по точным формулам. b) Расчет по программе Fresnel 4.1 Pro,
прохождение излучения через линзу с учетом сферической аберации третьего
порядка.
. a) Геометрооптическая модель, расчет хода лучей через линзу
выполнен по точным формулам. b) Расчет по программе Fresnel 4.1 Pro,
прохождение излучения через линзу с учетом сферической аберации третьего
порядка.
[1] Абрамовиц М., Стиган И. Справочник по специальным функциям.-М.: Наука, 1979.
[2] Ильинский Р. Е. Использование геометрооптической аналогии при расчете потерь в соединителе двух одномодовых волокон // Оптика и спектроскопия.-2003-Т.97, №1.-С.159-164.
[3] R. Ilinsky A Geometrical-Optics Analogue of a Astigmatic Elliptic Gaussian Beam// Progress in Optics Research New York : Nova Science Publishers, 2007. Editors: Maximilian N. Schulz pp. 293-304
[4] Ананьев Ю.А. Оптические резонаторы и лазерные пучки. - М.: Наука. Гл. ред. физ.-мат. лит., 1990. - 264 с.
[5] Абрамочкин Е.Г., Волостников В.Г. Современная оптика гауссовых пучков - М. Физматлит, 2010, 184с.
[6] A. E. Siegman, LASERS, University Science Books, Mill Valley, 1986. 1283pp
[7] И. В. Епатко и др. Новый алгоритм численного моделирования распространения лазерного излучения// Квантовая электроника, т. 25, N8 1998г. 717-722
[8] Д. А. Соловьев, Р.В. Серов, Расчет сферической аберрации линзы в задачах распространения лазерного излучения в оптических системах// Оптика и спектроскопия.-2001-Т.91, №2.-С.344-351.
[9] Заказнов Н. П., Кирюшин С. И., Кузичев В. И. Теория оптических систем.-М.: Машиностроение, 1992.-448с.
[10] Мосягин Г. М., Немтинов В. Б., Лебедев Е. Н. Теория оптико-электронных систем.- М.: Машиностроение,1990.- 432 с.
[11] Сапожников Р. А. Теоретическая фотометрия. Изд. 3-е, перераб. и доп. М., "Энергия", 1977. 264с.
[12] E.R.Freniere, G.G.Gregory and R.A.Hassler Proc SPIE 3780 151 (1999) Edge diffraction in Monte Carlo ray tracing.