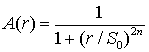Типичные проблемы восстановления изображений: дефокусировка и смазанное изображение. Результаты применения метода опорного изображения

 

А. Ю. Зражевский, В. А. Коротков, К. В. Коротков
ИРЭ им. В.А.Котельникова РАН,  Фрязинский филиал

 

Статья получена 3 апреля 2014 г.

 

Аннотация. В работе рассмотрены проблемы восстановления изображений при дефокусировке и смазанном изображении при сравнении результатов применения метода опорного изображения и фильтрации по методу Винера.

Ключевые слова: радиовидение, миллиметровый диапазон волн, аппаратная  функция, радиотепловое изображение, восстановление изображения, опорное изображение, метод Винера, метод опорного изображения.

Abstract: The paper considers the problems of restoring images on fussing and a blurred image. The results of the basic image method are compared with the results of  filtration on Winer's method.

Key words: radio vision, millimetric wave band, hardware function, radio thermal image, recovery of the image, basic image, Winer's method, method of the basic image.

 

         Восстановление дефокусированных и смазанных изображений принято рассматривать на основе уравнения свертки в силу относительной простоты решения этого уравнения с помощью преобразования Фурье [1,2]:

,                                                                    (1)

 

где D – область наблюдения,  - элементарная площадка в точке (x,y),  -  аппаратная функция (АФ) системы, - исходное  изображение,- изображение на выходе этой системы, - аддитивный шум.

В силу того, что смазывание изображений можно рассматривать как одномерную дефокусировку,  в дальнейшем рассмотрении ограничимся именно анализом этого случая. При этом возникающие проблемы сводятся к определению аппаратной функции (АФ) и учету влияния помех и шумов. Однако все это будет верно только при условии, что все объекты, изображения которых получают с помощью данной АФ, находятся на одном расстоянии от оптической системы, а изменение этого расстояния внутри поверхности, изображение которой строится, незначительно. Только при этом условии АФ может быть одинакова для разных объектов. Если это условие не выполняется, то уравнение (1) может быть записано так:

,                                                           (2)

 

где D – область наблюдения,  - элементарная площадка в точке (x,y),  -  аппаратная функция (АФ) системы для  объекта (исходного изображения), -  исходное  изображение,- изображение на выходе этой системы, - аддитивный шум, суммирование по  ведется по k объектам, стоящим на разном расстоянии от оптической системы.

Если перейти к спектральным представлениям изображений: исходного  и на выходе системы :

,

,                                                                        (3)

 

и спектра АФ:

,                  

                                           

то  в частотной области пространственный спектр  изображения на выходе системы выражается через спектр  и :

.                                                                (4)

         Понятно, что решить (4) относительно , даже если точно известны ,  и , невозможно. Однако можно и не ставить такой цели.

Если умножить обе части (4) на и применить обратное преобразование Фурье, то мы не получим в результате части, соответствующей , восстановленного изображения даже в отсутствии шума (). Это происходит из-за того, что для остальных элементов изображения  при  и при определенных пространственных частотах отношение  может принимать большие значения. Такой результат в какой-то степени похож на результат воздействия шума  при инверсной фильтрации [1]. Поэтому можно предположить, что применение адаптивного метода опорного изображения - аМОИ [3] или метода фильтрации по Винеру [1] с подбором коэффициента  эквивалентного отношению шум/сигнал будет успешно. Практика показывает, что это не так. Сформируем изображение, представленное на Рис.1А, состоящее из комбинации 3 изображений. Применим к отдельным частям изображения аппаратную функцию, аналогичную фильтру Баттерворта [1] с различными параметрами:

 ,                                                                                   (5)

где  - аппаратная функция,  - модуль ,  и  - параметры фильтра Баттерворта, и получим изображение на Рис.1Б. На Рис.1Б  и  принимает значения для разных частей изображения 0, 4.5, и 9.

 

Рис.1. А - исходное изображение и Б - изображение после применения к Рис.1А АФ (1) с  и  равной 0, 4.5, и 9. Размер изображений 306 х 460.

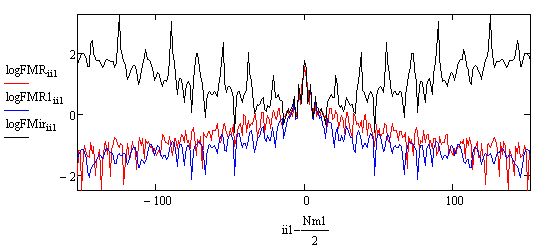
         На Рис.2 представлены графики разрезов модулей амплитудных спектров изображений, показанных на Рис.1.

 

Рис.2. Графики разрезов модулей спектров изображений, приведенных на Рис.1, в логарифмическом масштабе. Красная и синяя линии соответствуют Рис.1А и Рис.1Б. Черная линия обозначает график разреза модуля спектра, показанного на Рис.1Б после инверсной фильтрации с АФ (1) и , .

         Анализ графиков Рис.2 показывает, что амплитудные спектры изображений, приведенных на Рис.1А и Рис.1Б, похожи. В тоже время инверсная фильтрация (черный график на Рис.2) сильно искажает спектр изображения. Восстановление изображения после инверсной фильтрации с помощью аМОИ [3] и фильтрации по Винеру [1], как и ожидалось, не приводят к успеху. На Рис.3А и Рис.3Б приведены результаты восстановления изображения, показанного на Рис.1Б, соответственно с помощью аМОИ и метода Винера.

Увеличение  в методе Винера приводит к уменьшению «интерференционной» структуры на получаемом изображении и «замыливанию» деталей изображения. Постепенно, с увеличением , восстановленное с помощью метода Винера изображение будет приближаться к изображению, приведенному на Рис.3Б, полученному с помощью аМОИ.
 

Рис.3. Восстановление изображения, приведенного на Рис.1Б, с помощью аМОИ – А, метода Винера – Б при , и .
 

         Одним из вариантов решения проблемы восстановления может быть разбиение восстанавливаемого изображения на фрагменты и восстановление каждого фрагмента отдельно от остальных. Важным моментом может стать определение размера фрагмента. Из общих соображений понятно, что этот размер не следует делать меньше  характерного размера пятна расфокусировки -го объекта. В то же время величину фрагмента целесообразно делать меньше величины отдельного объекта изображения.  

В качестве примера Рис.2Б был разбит на квадратные фрагменты – спрайты, и каждый спрайт восстанавливался отдельно, но с одинаковыми параметрами АФ для всего изображения Рис.2Б. В качестве параметров аппаратной функции (5) используется , а  принимает значения 4.5 и 9 для восстановления разных частей изображения. Результат восстановления представлен на Рис.4.
 

Рис.4. Восстановление изображения, приведенного на Рис.1Б, с помощью аМОИ. АФ – фильтр Баттерворта . Вариант восстановления  соответствует Рис.4А,  - Рис.4Б. Количество спрайтов 3 х 4.
 

         Сравнение результатов восстановления, представленных на Рис.3-4, показывает преимущество восстановления описанным способом, то есть путем разбиения изображения на спрайты с последующим использованием аМОИ.
 

Рис.5. Восстановление изображения Рис.1Б с помощью аМОИ. АФ – фильтр Баттерворта . Вариант восстановления  соответствует Рис.5А,  - Рис.5Б. Количество спрайтов 6 х 9.

 

         На Рис.5 представлены результаты восстановления изображения, показанного на Рис.1Б, с помощью аМОИ. В отличие от результатов, представленных на Рис.4, восстановление изображения на Рис.5 производилось в 4 раза большим количеством спрайтов. Как мы видим на Рис.4-5, такое увеличение количества спрайтов не сильно сказывается на качестве восстановления.  

 

A

Б

В

 

Рис.6. Восстановление изображения Рис.6А с помощью аМОИ. АФ – фильтр Баттерворта . Вариант восстановления  соответствует Рис.6Б,  - Рис.6В. Количество спрайтов 3 х 4.
 

С помощью цифрового фотоаппарата SONY A550 было получено изображение, представленное на Рис.6А. Результаты восстановления Рис.6А представлены на Рис.6Б и Рис.6В. Как следует из анализа Рис.6, простым изменением параметра  можно по выбору восстанавливать (компенсировать дефокусировку) у соответствующих частей изображения.

         Если изображение состоит их нескольких объектов, но у некоторых параметры дефокусировки близки, то вне зависимости от того, что они могут находиться на разном расстоянии, результат восстановления для этих объектов будет одинаковый. С помощью цифрового фотоаппарата SONY A550 было получено изображение, представленное на Рис.7А. На изображении видно 3 объекта, находящихся на разном расстоянии, но дефокусировка ближнего и дальнего объекта близка. Поэтому результат восстановления для этих объектов похож – Рис.7Б.
 

Рис.7. Восстановление изображения Рис.7А 304х456 с помощью аМОИ. Рис.7А – исходное изображение. Рис.7Б - восстановленное изображения (АФ – фильтр Баттерворта ,, количество спрайтов 6 х 9).

Выводы.

Восстановление дефокусированных и смазанных изображений осложняется наличием помех и шумов в измеренном изображении, ошибками в определении формы и параметров аппаратной функции. Эти проблемы могут в той или иной мере быть решены в рамках известных методов, например метода опорного изображения или метода фильтрации по Винеру. Наличие на изображении нескольких по разному дефокусированных объектов делает применение этих методов малоэффективным. Разбиение обрабатываемого изображения на набор фрагментов (спрайтов) и дальнейшая обработка их с помощью аМОИ позволяет решить эту проблему.

 

Литература

1.     Р. Гонсалес,  Р. Вудс. Цифровая обработка изображений. М. «Техносфера» , 2005, 1071 стр.

2.     А. Ю. Зражевский, А. В. Кокошкин, Е.П. Новичихин, С.В. Титов, «Повышение качества  радиоизображений». «Нелинейный Мир», № 9, 2010г., с. 582-590.

3.     Ю. В. Гуляев, А. Ю. Зражевский, А. В. Кокошкин, В. А. Коротков,  В. А. Черепенин Коррекция пространственного спектра, искаженного оптической системой, с помощью метода опорного изображения.
Часть 2. Адаптивный метод опорного изображения (АМОИ).  // Журнал радиоэлектроники [электронный журнал]. 2013. №12.
URL: http://jre.cplire.ru/jre/dec13/2/text.html