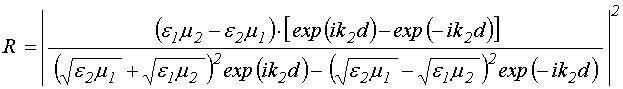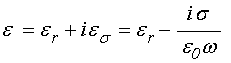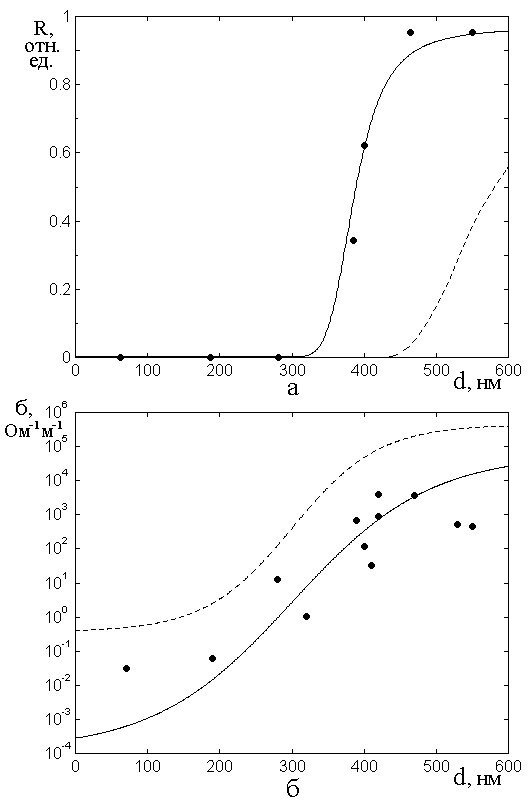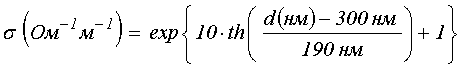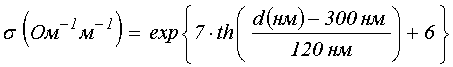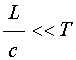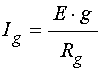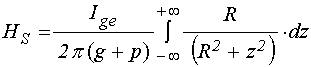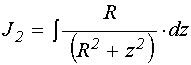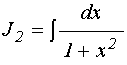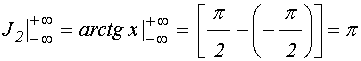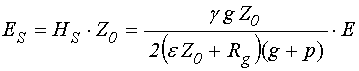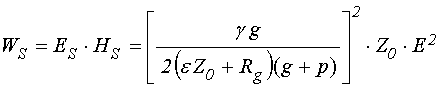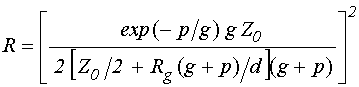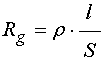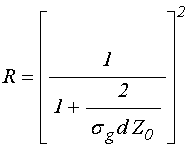Механизм динамической проводимости аморфных наногранулированных пленок в диапазоне сверхвысоких частот

УДК 537.874; 537.624

МЕХАНИЗМ ДИНАМИЧЕСКОЙ ПРОВОДИМОСТИ АМОРФНЫХ НАНОГРАНУЛИРОВАННЫХ ПЛЕНОК «МЕТАЛЛ-ДИЭЛЕКТРИК» В ДИАПАЗОНЕ СВЕРХВЫСОКИХ ЧАСТОТ

И. В. Антонец¹, Л. Н. Котов¹, О. А. Кирпичёва¹, Е. А. Голубев², Ю. Е. Калинин³, А. В. Ситников³, В. Г. Шавров⁴, В. И. Щеглов⁴

¹Сыктывкарский государственный университет, Сыктывкар, Россия

²Институт геологии Коми НЦ Уро РАН, Сыктывкар, Россия

³Воронежский государственный технический университет, Воронеж, Россия

⁴Институт радиотехники и электроники РАН, Москва, Россия

Статья получена 22 апреля 2014 г.

Аннотация. Экспериментально исследована статическая проводимость на постоянном токе и отражение электромагнитных волн СВЧ диапазона от тонких пленок гранулированных аморфных металл-диэлектрических нанокомпозитов. Выявлено превышение динамической проводимости над статической на два-четыре порядка. Для объяснения экспериментальных результатов предложена модель внутригранулярных (внутрикластерных) токов. Рассчитан коэффициент отражения СВЧ волны от пленок с учетом их гранулированного характера. Выявлен механизм компенсации полей отдельных гранул, приводящий к резкой зависимости коэффициента отражения от толщины пленок.

Ключевые слова: тонкие пленки, нанокомпозит металл-диэлектрик, отражение электромагнитных волн.

Abstract. In experiments the static conductivity on direct current and electromagnetic microwave reflectivity from thin nanogranulated amorphous composite metal-dielectric films were investigated. It was found the exceeding of dynamic conductivity over static on two-four orders. For the explanation of these experimental results the model of intergranular (intercluster) currents is proposed. The microwave reflection coefficient from films in connection with theirs granular character is found. It is proposed the mechanism of individual granular fields compensation which leads to sharp dependence of reflection coefficient from film thickness.

Key words: thin films, nanocomposit metal-dielectric, electromagnetic wave reflection.

Введение

В последнее время значительное внимание исследователей, техников и технологов привлекают наногранулированные композиты «металл-диэлектрик» [1-4], в том числе содержащие магнитные наночастицы и , проявляющие уникальные анизотропные и структурные свойства [5,6]. В технике СВЧ все большее значение приобретают метаматериалы – композиты, состоящие из множества отдельных элементов, в том числе фотонные и магнонные кристаллы, проявляющие «левые» волноведущие свойства [7-11]. Наноструктурные гранулированные металл-диэлектрические пленки могут быть отнесены к особому классу подобных материалов, распределение гранул внутри которых носит хаотический характер [12]. Использование ферромагнитного металла в такой наноструктуре обусловливает как проявление гигантского магнитосопротивления [13], так и высокий уровень поглощения СВЧ излучения [14].

Разнообразие прикладных возможностей таких материалов стимулирует изучение их физических свойств, в том числе квантовые механизмы электропроводности в сочетании с процессами намагничивания [5,6,15-18].

Для интерпретации электрических свойств гранулированных нанокомпозитов предложены модели прыжковой проводимости [18], активированного [17,19,20] и резонансного туннелирования [21,22], описывающие зависимость проводимости от температуры.

С другой стороны, и при комнатных температурах аморфные нанокомпозиты проявляют немало интересных свойств. В первую очередь это касается СВЧ процессов, где наблюдается аномальное уширение линии ФМР [23] и аномальные особенности электронного транспорта, изучаемые методами спин-волновой спектроскопии [24-26].

В работах [27,28], относящихся к аморфным металлическим пленкам без ярко выраженных гранул, однако имеющим кластерный характер, по-видимому, впервые было сообщено о различии статической и динамической СВЧ проводимостей таких пленок, могущем достигать полутора-двух раз.

Подобное различие проводимостей для аморфных наногранулированных пленок было отмечено в работе [29], однако приведенные там результаты являются предварительными. В работе [30], относящейся к гранулированным композитам состава , показано, что динамическая проводимость таких пленок в диапазоне СВЧ превышает статическую до четырех раз. Для объяснения этого явления предложены механизмы емкостного шунтирования, эффективной диэлектрической проницаемости и внутрикластерных токов. Механизм емкостного шунтирования также был привлечен для интерпретации описанного для тех же пленок в работе [31] увеличения коэффициента отражения с частотой, в диапазоне 10-25 ГГц достигающего полутора раз. В работе [32], где исследованы пленки состава , показано, что в этом случае различие динамической и статической проводимостей является гигантским и может достигать четырех порядков.

Однако исследования, описанные в этих работах, являются недостаточно полными. Так не ясно поведение пленок в более широком, чем в работе [31], диапазоне частот, в первую очередь адекватность емкостного механизма без привлечения роли контактов. О возможной роли механизма внутрикластерных токов в работе [30] лишь кратко упоминается, что не позволяет получить реальных числовых оценок. Не ясна причина столь большой величины превышения динамической проводимости над статической, как на три-четыре порядка.

Предварительные оценки показывают, что в пленках, описанных в работе [32], преобладающую роль может играть механизм внутрикластерных токов, в связи с чем настоящая работа посвящена более подробному его рассмотрению с целью интерпретации экспериментальных результатов.

1. Технология получения и морфологические свойства пленок

В работе исследовались пленки наногранулированных композитов состава , представлявших собой металлические гранулы Co-Fe-Zr, вкрапленные в диэлектрическую матрицу Zr₂O₃, причем концентрация металлической фазы составляла от 0.20 до 0.80. Пленки были получены методом ионно-лучевого напыления в атмосфере азота с применением методики экранирования [33,34] на гибких подложках из лавсана. Технология получения пленок была разработана в Воронежском государственном техническом университете и наиболее подробно описана в работах [34-37].

Гранулированный характер пленок проверялся методом просвечивающей электронной микроскопии [34,37-39]) на контрольных образцах, выполненных на подложках из NaCl в виде пленок толщиной до 100 нм. Аморфный характер металлических гранул определялся по высокой степени размытия кольцевых дифракционных гало на электронных микрофотографиях [34,40].

В настоящей работе было исследовано 12 образцов пленок размером с толщиной от 70 до 550 нм, которая контролировалась с помощью сканирующего электронного микроскопа путем наблюдения в торец по 15 точкам.

Топография поверхности пленок исследовалась с помощью атомно-силового микроскопа по методике, описанной в [27,28,41].

На всех пленках наблюдался четко выраженный зернистый характер поверхности, подобный описанному в [27,28,41], размер зерен составлял от 30 до 100 нм и увеличивался с увеличением толщины пленки.

2. Измерение электрических параметров пленок

Основным предметом исследования в настоящей работе была удельная электрическая проводимость пленок, определяемая двумя методами: по удельному сопротивлению пленок на постоянном токе и по коэффициентам отражения и прохождения электромагнитных волн в диапазоне СВЧ.

3. Измерение статической проводимости

Статическая удельная проводимость получалась как обратная величина удельного электрического сопротивления, измеряемого на постоянном токе двухзондовым методом с использованием потенциометрической методики замещения [27,28]. Было выявлено, что удельная проводимость исследуемых пленок меняется в диапазоне от до и увеличивается с увеличением концентрации металлической фазы.

4. Измерение коэффициентов отражения и прохождения

Отражение СВЧ электромагнитных волн от пленок и прохождение волн через них исследовалось в трех диапазонах частот: 8-11, 12-18 и 24-38 ГГц. Измерения проводились с помощью комплекта панорамных волноводных СВЧ спектрометров, включавших в себя генератор качающейся частоты в сочетании с индикатором коэффициента стоячей волны напряжения (КСВН) по методике, аналогичной описанной в работах [27-29,31]. В отличие от работы [31], где коэффициент отражения измерялся по напряжению, в настоящей работе, подобно [27-29], коэффициенты отражения и прохождения измерялись по мощности. Отражение волн СВЧ от материала подложки во всех диапазонах не превышало 5%.

5. Основные статические параметры пленок

Основные статические параметры пленок приведены в таблице №1. Концентрация металлической фазы и толщина были заданы технологически, а проводимость на постоянном токе измерялась по описанной в предыдущем разделе методике. Средняя точность измерения толщины составляла 9%. Средняя точность измерения проводимости составляла 35%.

Пленки расположены в порядке увеличения концентрации основных проводящих металлов Fe+Co. Такой параметр для упорядоченности расположения пленок выбран по той причине, что в объемном состоянии удельные проводимости железа и кобальта почти на порядок превышают удельную проводимость аморфизатора циркония [42], поэтому, учитывая что цирконий составляет в общем составе металлической фазы сплава всего 10%, его вклад в качестве проводника в результирующую проводимость пленок является второстепенным. Для справки в следующем столбце таблицы приведено общее значение концентрации ( в химических формулах составов пленок) Fe+Co+Zr. Видно, что с увеличением концентрации Fe+Co величина общей концентрации тоже, в основном, возрастает.

Следует учитывать далее, что в аморфных пленках удельная проводимость металлов, таких как Fe и Co, по крайней мере на порядок меньше, чем в объемных образцах, [27,28], поэтому для численных оценок приведенные выше значения должны быть уменьшены в таком же соотношении.

Таблица №1.

№№ (исх.)	Концентрация		Толщина (нм)	Проводимость (Ом^-1м^-1)
№№ (исх.)	Fe+Co	Fe+Co+Zr	Толщина (нм)	Проводимость (Ом^-1м^-1)
1	0.14	0.25
2	0.27	0.38
3	0.37	0.54
4	0.45	0.59
5	0.46	0.63
6	0.53	0.65
7	0.58	0.68
8	0.60	0.73
9	0.64	0.77
10	0.65	0.75
11	0.68	0.78
12	0.68	0.77

Из таблицы видно, что при увеличении концентрации металлической фазы удельная проводимость пленок возрастает. Численная оценка показывает, что при концентрациях меньше 0.2 и больше 0.6 зависимость удельной проводимости от концентрации металлической фазы можно приближенно (с точностью до двух-трех раз) описать с помощью эмпирической формулы:

. (1)

За пределами интервала концентрации (0.2 – 0.6) лучшее приближение обеспечивает плавный переход проводимости к насыщению. Такое насыщение обусловлено тем, что стремлении концентрации к нулю пленка становится полностью диэлектрической с проводимостью около , а при стремлении к единице – полностью металлической с проводимостью около .

Сравним полученные результаты с параметрами пленок, исследованных в работе [30]. Рассмотренные там пленки имели составы: (серия А) и (серия Б), где . При этом, если судить по приведенному там интервалу концентраций, удельная проводимость диэлектрической фазы составляла порядка , а металлической – . Можно видеть, что для тех пленок удельная проводимость как диэлектрической, так и металлической фаз была на 3-5 порядков выше, чем для рассматриваемых в настоящей работе. При этом металлы основной фазы Fe и Co – те же, тогда как металлы диэлектрической фазы – другие: Mg, для которого и Al, для которого [42]. В рассмотренных здесь пленках эти металлы заменены относительно плохо проводящим цирконием ( [42]), что, по-видимому, и приводит к уменьшению удельной проводимости диэлектрической фазы на пять порядков. С другой стороны, можно думать, что столь сильное уменьшение проводимости диэлектрической фазы оказывает влияние на уменьшение проводимости также и металлической фазы, что дает и ее уменьшение на три порядка. Дополнительным фактором уменьшения проводимости обеих фаз могут явиться вносимые цирконием структурные изменения, обоснование чего требует дополнительных структурных исследований, выходящих за рамки настоящей работы.

6. Отражение волн СВЧ от пленок

Рассмотрим теперь динамическое поведение проводимости пленок на основе экспериментов по отражению электромагнитных волн СВЧ диапазона. Будем в основном следовать результатам работы [32], где описаны предварительные эксперименты на тех же пленках.

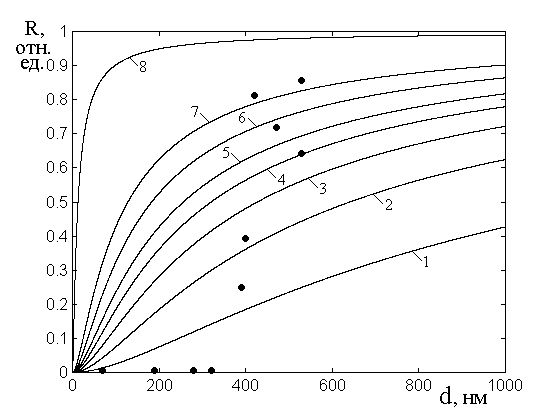
На рис.1 показаны зависимости от толщины пленок для коэффициента отражения на частоте 16 ГГц (а) и удельной проводимости на постоянном токе (б).

Рассмотрим сначала зависимость коэффициента отражения от толщины пленок , показанную на рис. 1а. Здесь точки – результаты эксперимента. При расчете коэффициента отражения использовалась формула [43,44]:

(2)

где , , – проницаемости и волновое число в свободном пространстве, , , – проницаемости и волновое число в пленке, – толщина пленки. Проводимость пленки учитывалась в виде мнимой добавки к диэлектрической проницаемости с помощью формулы:

, (3)

где - диэлектрическая проницаемость пленки в отсутствие проводимости, - частота, - диэлектрическая постоянная.

Рис.1. Зависимость коэффициента отражения (а) и удельной проводимости (б) от толщины пленок.

В расчетах полагалось, при частоте ( = 16 ГГц) в свободном пространстве: , , , в материале пленок в отсутствие проводимости: , , .

Входящая в формулу (3) проводимость рассчитывалась по значениям, приведенным в таблице №1, приближенным с помощью эмпирической формулы:

, (4)

соответствующей сплошной кривой на рис.1б. При этом для коэффициента отражения была получена кривая, показанная на рис.1а пунктирной линией, то есть резко не соответствующая эксперименту.

Сплошная кривая на рис.1а, проходящая по экспериментальным точкам, построена с использованием вместо (4) следующей формулы:

. (5)

Однако использование этой формулы для построения зависимости проводимости от толщины, на рис.1а дает пунктирную кривую, лежащую значительно выше и левее сплошной, проходящей по экспериментальным точкам полученным на постоянном токе, причем превышение составляет от двух до четырех порядков.

Таким образом, если рассматривать измерение коэффициента отражения как метод для измерения динамической проводимости пленок (на СВЧ), то можно видеть, что такая проводимость превышает статическую на два-четыре порядка.

Как уже упоминалось, некоторое (около двух раз) превышение динамической проводимости над статической отмечалось ранее на металлических пленках, имеющих зернистую структуру [27,28], а также до четырех раз на гранулированных пленках с более высокой чем здесь (на 3-5 порядков) удельной проводимостью [30].

Можно полагать, что наблюдаемое здесь превышение динамической проводимости над статической на несколько порядков, связано, во-первых, именно с гранулированной структурой композитных пленок, и во-вторых, со сравнительно низкой удельной проводимостью в первую очередь диэлектрической фазы, обусловленной наличием в ее составе низкопроводящего циркония.

7. Отражение в диапазоне частот

Приведенные в предыдущем разделе данные соответствуют единственной частоте 16 ГГц. Рассмотрим теперь отражение электромагнитных волн от пленок в широком диапазоне частот.

На рис.2 показаны зависимости коэффициента отражения от частоты для ряда пленок, выбранных таким образом, чтобы более или менее равномерно перекрыть весь возможный интервал значений коэффициента отражения от нуля до единицы. Точность измерения коэффициента отражения во всем диапазоне частот составляет не менее 10%. Экспериментальные точки соответствуют практически непрерывному изменению частоты. Отсутствие данных между 18 и 24 ГГц обусловлено отсутствием имевшихся в распоряжении авторов набором приборов (панорамных спектрометров).

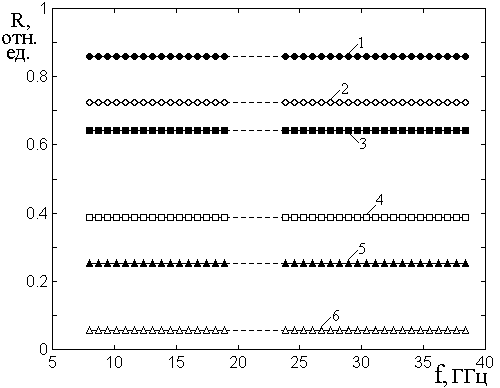
Рис.2. Зависимости коэффициента отражения от частоты для ряда пленок.
Кривая 1 соответствует пленке №11, кривая 2 – пленке №10, 3 – № 9, 4 – №6, 5 – №8, 6 – №5.

Из рис.2 видно, что зависимость коэффициента отражения от частоты в исследованном диапазоне частот 8-38 ГГц с точностью до 10% отсутствует. Заметим, что наблюдаемое отсутствие частотной зависимости не соответствует наблюдавшемуся в работе [31] подъему в области выше 25 ГГц, что, возможно, связано с различным характером пленок, исследованных здесь и в работе [31]. С другой стороны, подобное наблюдаемому здесь отсутствие частотной зависимости отражения хорошо известно для тонких пленок, обладающих металлическим характером проводимости [45,27]. Более того, в работе [46] показано, что частоты, при которых металлический характер отражения сменяется диэлектрическим, обусловливающим сильную осциллирующую зависимость отражения от частоты, составляют тысячи, десятки и сотни тысяч ГГц, то есть лежат намного выше диапазона, исследованного как в [31], так и в настоящей работе.

8. Сравнение динамических свойств со статическими

Из рассмотрения приведенных экспериментов следуют два основных вывода:

1) динамическая проводимость аморфных наногранулированных пленок более чем на два порядка превышает статическую;

2) динамические свойства пленок в диапазоне 8-40 ГГц от частоты не зависят.

9. Оценка роли емкостного механизма

Из второго вывода, находящегося в некотором противоречии с данными работы [31], сразу следует ограниченность действия емкостного механизма. Уделим некоторое внимание емкостному механизму динамической проводимости в таком виде, как он был предложен в работе [31]. Рассмотрим рис.4 из статьи [31]. Можно видеть, что коэффициент отражения с частотой возрастает для пленок, состав которых ниже (кривые 1,2) или вблизи (кривая 3) порога перколяции. Для интерпретации такого факта привлекается емкостная модель (рис.5, форм. (2)), в которой для оценки емкости промежутка между гранулами используется формула плоского конденсатора (3):

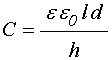, (6)

для подстановки в которую используются параметры:

, , , , , откуда получаются минимальное и максимальное значения емкости: , . Далее максимальное (и даже слегка завышенное) из этих значений подставляется в формулу (2), в результате чего получается зависимость «модуля комплексной проводимости» от частоты, приведенная на рис.6.

Таким образом, следуя обозначениям статьи [31], полагается, что структура пленки образована гранулами с «поперечными размерами , длиной и толщиной » (обозначения расшифрованы в первых трех строках левого столбца текста после формулы (2) на стр.1197), то есть гранулы имеют размеры: .

При таких размерах гранула представляет собой длинную тонкую нить, протяженную от одной поверхности пленки до другой, причем длина такой нити отличается от ее толщины на три (!) порядка. Однако из литературы известно [12-18, 34], что гранулы обычно имеют более или менее сферическую форму.

С другой стороны, согласно [34], гранулы в некоторых случаях все же могут иметь вытянутую «столбчатую» форму, обусловленную магнитным и обменным взаимодействием компонент сплава в процессе роста. Именно такая «столбчатость» обеспечивает магнитную анизотропию с осью, перпендикулярной плоскости пленки (10-20 Э). Однако прямое исследование формы «столбчатых» гранул, выполненное в работе [34, стр.176] методом электронной микроскопии, показало, что длина «столбчатых» гранул составляет , но никак не приведенное в работе [31] значение .

Таким образом, можно полагать, что правомерность использования в работе [31] в качестве одного из размеров гранул величины является не вполне корректной или требует более серьезного обоснования.

С другой стороны, если использовать в качестве размера гранул величину более реальную (порядка 5-10 нм), то получаемая емкость составляет порядка , что примерно соответствует полученному в работе [30] значению .

Там же показано, что такая емкость для интерпретации наблюдаемых эффектов недостаточна, в результате чего для объяснения результатов эксперимента привлечен механизм межконтактной емкости, который как раз и дает , то есть – то самое значение, которое использовано в работе [31]. Именно такое значение емкости как раз и обеспечивает превышение динамической проводимости над статической в несколько (до четырех) раз.

Отметим дополнительно, что емкостная модель в любом случае должна приводить к зависимости коэффициента отражения от частоты, отмеченную в экспериментах, описанных в работе [31]. К сожалению, в работе [30] частотные эксперименты отсутствуют (все измерения проводились на одной частоте 14 ГГц). Тем не менее, учитывая приведенные оценки, можно полагать, что частотная зависимость, приведенная в работе [31], обусловлена не межкластерным, а именно межконтактным механизмом, имеющим ту же емкостную природу.

10. Оценка роли различных механизмов

В соответствии со сказанным, из первого вывода о весьма значительном превышении динамической проводимости над статической можно заключить, что роль емкостного механизма в общем случае довольно невелика. Поэтому имеет смысл более подробно рассмотреть альтернативные механизмы, наиболее перспективным из которых в плане интерпретации экспериментальных результатов, по-видимому, является механизм внутрикластерных или внутригранулярных токов.

Так, из первого вывода следует, что отражающие свойства пленок резко отличаются от отражающих свойств диэлектрика и приближаются к отражающим свойствам металла. То есть, если рассматривать реакцию диэлектрика на электрическое поле как результат поляризации молекул, а реакцию металла на такое же поле как результат протекающих в нем токов, можно полагать, что в случае аморфных наногранулированных пленок в формировании проводимости решающую роль играет именно токовый механизм, то есть токи в проводящих областях таких пленок, а именно в гранулах и в какой-то степени в кластерах, образованных компактными группами из гранул. Поэтому далее рассмотрим механизм внутригранулярных токов более подробно.

11. Модель внутригранулярных токов

При наличии в пленке проводящих областей, размер которых недостаточен для возникновения перколяции, проводимость на постоянном токе отсутствует. Однако, волна СВЧ в таких проводящих областях возбуждает токи, которые создают магнитные поля той же частоты. Эти поля можно рассматривать как источник вторичных волн, создаваемых первичной падающей волной. То есть можно считать, что волна переизлучается такими областями за счет циркулирующих в них токов. Переизлучение происходит в обе стороны относительно поверхности пленки, за счет чего формируются как отраженная, так и проходящая волны. Таким образом, присутствие внутри пленки локализованных не контактирующих между собой проводящих областей должно увеличивать коэффициент отражения и уменьшать коэффициент прохождения волны еще задолго до порога перколяции, тем сильнее, чем размер таких проводящих областей больше.

В реальных пленках имеются хорошо проводящие металлические гранулы, разделенные тонкими диэлектрическими прослойками. Гранулы сгруппированы в кластеры, промежутки между которыми ниже порога перколяции превышают размеры гранул. При увеличении концентрации металлической фазы промежутки уменьшаются, так что на подходе к перколяции основную часть объема пленок составляют уже более или менее равномерно распределенные металлические гранулы. То есть в первом приближении можно считать, что СВЧ проводимость пленок, особенно вблизи порога перколяции, определяется именно близко соседствующими гранулярными включениями металлической фазы.

12. Проверка применимости условий квазистационарности

Для расчета поля волны, отраженной от проводящего тела, вообще говоря, надо пользоваться полными уравнениями электродинамики. Однако, при малом размере отражающего тела, когда запаздывание волны при прохождении от одного конца тела до другого достаточно мало, можно пользоваться упрощенными уравнениями квазистационарности. Условие квазистационарности имеет вид [47]:

, (7)

где – характерный размер тела, – скорость света, – период падающей волны.

Характерный размер гранулы составляет , толщина пленки – менее 1 мкм, то есть . Скорость света – . При таких параметрах левая часть соотношения (7) для одной гранулы равна и для толщины пленки в целом – . Наивысшая частота в пределах рассмотренных в настоящей работе диапазонов волн составляет порядка 40 ГГц, то есть период равен , что на четыре-шесть порядков превышает полученные величины. Таким образом, в пределах как одной гранулы, так и толщины всей пленки в целом условия квазистационарности полностью выполняются, чем и воспользуемся далее.

13. Поле одной гранулы

Рассмотрим сначала образование полей отраженной и проходящей волн при падении электромагнитной волны на одну из проводящих (металлических) гранул.

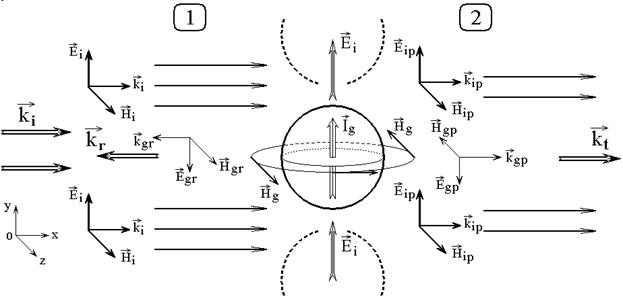
Рис.3. Схема образования полей отраженной и проходящей волн при падении электромагнитной волны на одну гранулу.

На рис.3 показана общая схема образования таких полей. Ориентация осей декартовой системы координат приведена в левом нижнем углу рисунка. Плоскость пленки (на рисунке не показана), параллельная координатной плоскости , разграничивает две области свободного пространства, обозначенные цифрами 1 и 2.

Пленка представляет собой однослойную сетку из гранул, одна из которых (в данном случае сферической формы) показана в центре рисунка. Контур этой гранулы выделен утолщенной линией. Выше и ниже рассматриваемой гранулы находятся другие такие же сферические гранулы, контуры которых показаны пунктирными утолщенными линиями. Будем полагать, что процессы во всех гранулах происходят одинаково, поэтому достаточно более подробно рассмотреть только одну гранулу.

Пусть на пленку из области 1 падает плоская электромагнитная волна, волновой вектор которой параллелен оси , вектор электрического поля параллелен оси , магнитного – оси . Показанные на рисунке ориентации полей волны соответствуют одному из полупериодов во времени, в другом полупериоде направления полей будут обратными. Электрическое поле падающей волны , попадая на металлическую гранулу, создает в ней переменный во времени ток , вектор которого направлен вдоль оси . Этот ток создает вокруг себя циркулирующее магнитное поле , вектор которого в данный полупериод времени в области 1 ориентирован в положительном направлении оси , а в области 2 – в отрицательном. Будучи переменным во времени, магнитное поле создает в области 1 вторичную электромагнитную волну с волновым вектором и полями , , распространяющуюся в отрицательном направлении оси .

В этой волне знак магнитного поля совпадает со знаком поля исходной волны , а знак электрического поля меняется относительно знака на противоположный. Однако синхронного суммирования полей этих волн не происходит, так как их направления распространения противоположны. Сложение полей от разных гранул в этой области дает суммарную отраженную волну с волновым вектором , распространяющуюся в отрицательном направлении оси .

Создаваемое гранулой поле в области 2 создает вторичную электромагнитную волну с волновым вектором и полми , , распространяющуюся в положительном направлении оси . Кроме этой вторичной волны в область 2 проникает из области 1 падающая волна с полями и , ослабленная за счет потери энергии при возбуждении тока в гранулах, так что , . Во вторичной волне, образованной за счет тока в грануле, знаки как магнитного , так и электрического полей противоположны знакам полей и . Однако, благодаря совпадению направлений распространения обеих волн, их поля суммируются, давая в результате поля: электрическое и магнитное . Сложение таких разностных полей от всех гранул в этой области дает суммарную проходящую волну с волновым вектором , распространяющуюся в положительном направлении оси .

14. Образование отраженной и проходящей волн в случае многослойной пленки

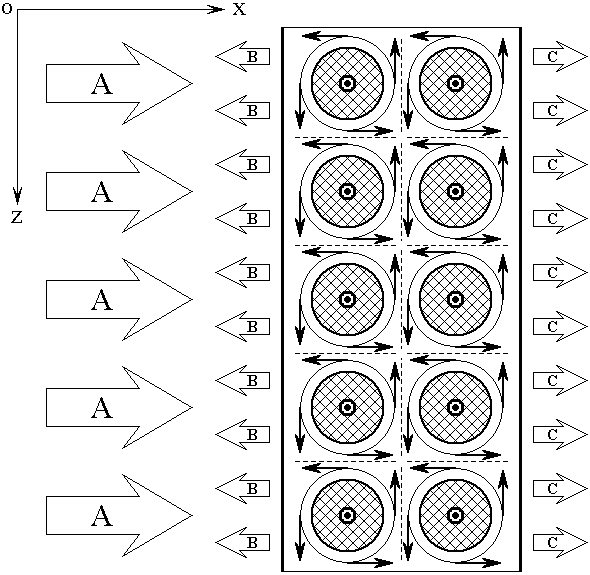
Проведенное рассмотрение относится к пленке, содержащей один слой гранул. Однако в реальных пленках гранулы могут располагаться в несколько слоев, образуя сложную пространственную структуру. В этом случае поля от соседних слоев гранул, будучи направленными в противоположные стороны, взаимно компенсируются (подобно молекулярным токам Ампера) [48,49], в результате чего решающую роль в формировании отраженной и проходящей волн играют только поверхностные слои гранул по обе стороны поверхности пленки.

Схема образования отраженной и проходящей волн иллюстрируется рис.4, где показан вид поперечной структуры пленки в плоскости (система координат – та же, что на рис.3) со стороны положительного направления оси (перпендикулярной плоскости рисунка). Заштрихованными кругами изображены гранулы, находящиеся в окружающей их диэлектрической матрице. С левой стороны на пленку падает волна А (большие стрелки). Электрическое поле этой волны, направленное вдоль оси , возбуждает в гранулах токи, концы векторов которых показаны в центре гранул укрупненными точками с кольцевой окантовкой. Эти токи вызывают магнитные поля, силовые линии которых показаны окружающими гранулы тонкими линиями, а касательные к ним утолщенные стрелки соответствуют положениям векторов магнитных полей вдоль осей и .

Рис.4. Схема образования отраженной и проходящей волн.

Из рис.4 видно, что между гранулами (на линиях, показанных пунктиром) магнитные поля соседствующих гранул взаимно компенсируются. Нескомпенсированными остаются поля только тех гранул, которые примыкают непосредственно к внешним поверхностям пленки. Именно эти поля создают отходящие от поверхностей пленки волны В и С (малые стрелки). Волна В представляет собой отраженную волну. Волна С в сумме с той частью падающей волны, которая проходит насквозь через пленку, образует проходящую волну.

15. Аналитическое рассмотрение образования поля вторичной волны

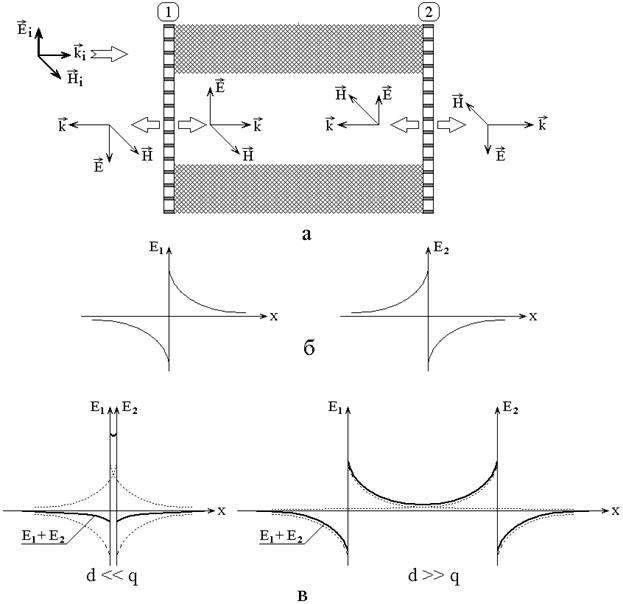
Рассмотрим теперь количественные соотношения при образовании поля вторичной волны, как это иллюстрируется рис.5.

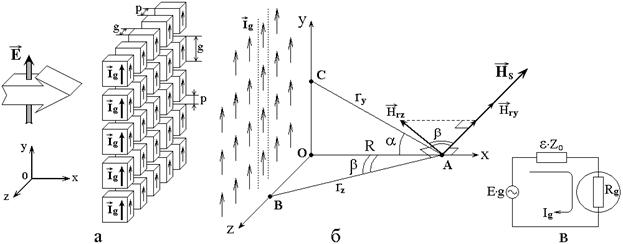
Рис.5. Схема образования поля вторичной волны.

а – образование токов в гранулах; б – образование суммарного поля от токов в гранулах; в – схема образования тока внутри гранулы.

На рис.5а показана схема пленки и падения на нее электромагнитной волны. Для простоты полагаем, что пленка представляет собой плоский слой одинаковых гранул кубической формы, расположенных в виде правильной квадратной решетки. Длина ребра куба гранулы равна , промежутки между гранулами равны . На пленку по нормали падает волна, электрическое поле которой равно (рис.5а). Плоскость декартовой системы координат параллельна плоскости пленки. Направление распространения волны совпадает с осью , поле волны параллельно оси .

Такое поле вызывает в гранулах токи , равные

, (8)

где – сопротивление гранулы постоянному току. В плоскости пленки токи, локализованные в отдельных гранулах, образуют плоскую структуру, параллельную плоскости , показанную на рис.5б слева. Такую структуру можно рассматривать как образованную стоящими вплотную друг к другу вертикальными цепочками последовательно расположенных гранул. В качестве примера одна цепочек показана ограничивающими ее вертикальными точечными линиями.

Поскольку гранулы разделены непроводящими промежутками, сплошной ток вдоль оси через такую цепочку отсутствует, однако внутри каждой гранулы протекает ток, с каждым полупериодом волны меняющий направление. Образование такого тока в единичной грануле иллюстрируется рис.5в. На длине гранулы вдоль оси поле волны имеет разность потенциалов . При этом волна по отношению к грануле является источником тока с внутренним сопротивлением, пропорциональным импедансу свободного пространства , где – нормировочный коэффициент, значение которого определим далее (не путать с диэлектрической проницаемостью!). Таким образом, ток внутри гранулы образуется за счет приложения напряжения к последовательно соединенным двум сопротивлениям и . Этот ток равен:

. (9)

В результате протекания тока , гранула создает вокруг себя «вторичное» магнитное поле , причем такие поля от отдельных гранул суммируются, формируя в пространстве около пленки единое магнитное поле, параллельное оси .

Будем полагать, что результирующее суммарное поле создается непрерывным «эффективным» током, текущим вдоль цепочки гранул, величина которого несколько меньше и составляет:

, (10)

где можно положить стремящимся к единице при и к нулю при , например, в виде:

. (11)

При этом вблизи порога перколяции, когда размер промежутков между гранулами становится значительно меньше размера самих гранул , можно полагать .

Примем в качестве точки наблюдения точку А, удаленную от плоскости на расстояние (рис.5б).

Рассмотрим сначала поле, создаваемое цепочкой гранул, проходящей через начало координат – точку . В рамках квазистационарного приближения поле в точке А, создаваемое током в элементе цепочки при точке С, можно найти с помощью закона Био-Савара [47-49]:

, (12)

где:

, (13)

. (14)

Полное поле, создаваемое всей вертикальной цепочкой гранул, проходящей через точку , определяется интегралом:

. (15)

Рассмотрим вспомогательный интеграл:

. (16)

С помощью замены переменных:

, (17)

приведем его к виду:

. (18)

Введем еще одну замену переменных:

. (19)

При этом:

. (20)

Пользуясь известной тригонометрической формулой [50]:

, (21)

получаем:

. (22)

Пределы интегрирования в (15) при заменах (17) и (19) принимают вид:

, (23)

откуда получаем:

. (24)

Подставляя (24) в (15), получаем:

, (25)

что по структуре совпадает с формулой для поля, создаваемого током в прямом проводе [48,49], однако ток здесь определяется формулой (10).

Такое поле в точке А направлено вдоль оси , так как создается цепочкой гранул, проходящей через точку , являющуюся началом координат. Поле от цепочки гранул, проходящей через произвольную точку В оси , равно:

, (26)

где расстояние между точкой В и точкой наблюдения А равно:

. (27)

Это поле направлено перпендикулярно линии АВ, а его составляющая вдоль оси определяется формулой:

, (28)

где:

. (29)

Благодаря симметрии задачи, составляющая поля вдоль оси компенсируется такой же составляющей противоположного знака, создаваемой подобной же цепочкой гранул, расположенной по другую сторону оси , в результате чего суммарное поле в точке А получается направленным точно вдоль оси .

Для возможности интегрирования вдоль оси введем поверхностную плотность тока , приходящуюся на единицу длины оси :

. (30)

При этом ток в полосе шириной равен:

. (31)

Поле вдоль оси , создаваемое таким током в точке А равно:

, (32)

Полное поле, создаваемое в точке А всей совокупностью токов в плоскости пленки, направлено вдоль оси и равно:

, (33)

откуда с учетом (27) и (29), получаем:

, (34)

Рассмотрим вспомогательный интеграл:

. (35)

С помощью замены переменных:

, (36)

приведем его к виду:

. (37)

Этот интеграл является табличным и равен [50]:

. (38)

Пределы интегрирования при замене (36) принимают вид:

, (39)

откуда получаем:

. (40)

Подставляя (40) в (34), получаем:

, (41)

Подставляя в соответствии с формулой (10), получаем полное поле, создаваемое электрическим полем волны в точке А:

. (42)

Как видим, поле не зависит от расстояния от точки наблюдения А до плоскости пленки. Такая независимость является следствием бесконечной протяженности пленки в плоскости . При конечных пределах интегрирования, отличных от (23) и (39), такая зависимость имела бы место. Однако в реальных экспериментах пространственная протяженность пленки (единицы см) по крайней мере на четыре-пять порядков превышает как толщину пленки (сотни нм), так и размер гранул (единицы нм), поэтому приближение (23) и (39) можно считать достаточно хорошим.

С другой стороны, формула (42) для поля получена в приближении квазистационарности, то есть она применима только на расстояниях , значительно меньших . Наивысшая частота в описываемых здесь экспериментах – порядка 40 ГГц, то есть минимальный период волны равен . При этом , поэтому предел применимости формулы (42), будучи меньшим на порядок, составляет не более . Такое расстояние близко к одной десятой от длины волны, где амплитуда составляет примерно 0.81 от максимума. Таким образом, формулу (42) можно считать применимой с точностью порядка 20%.

16. Электрическое поле вторичной волны

Будем считать, что магнитное поле, создаваемое падающей волной, определяется формулой (42) непосредственно вблизи самой поверхности пленки. Такое поле присутствует на обоих поверхностях пленки, образуя вторичную отраженную и вторичную проходящую волны. В простейшем случае (без учета затухания) можно полагать, что магнитные поля обеих таких волн равны, откуда следует, что равны и электрические.

Так электрическое поле каждой из вторичных волн равно:

. (43)

17. Коэффициент отражения

Вторичные волны образуют потоки энергии, текущие в обе стороны относительно плоскости пленки, по абсолютной величине равные:

. (44)

При электрическом поле падающей волны , ее магнитное поле равно:

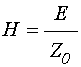. (45)

Поток энергии падающей волны равен:

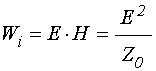. (46)

Из (44) и (46) получаем коэффициент образования вторичной волны по энергии:

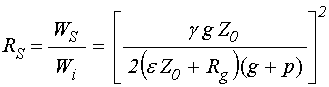. (47)

Рассматривая вторичную волну, распространяющуюся в направлении встречном относительно падающей волны, как отраженную, получаем коэффициент отражения по энергии:

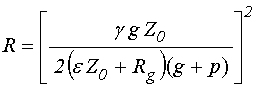. (48)

При полном смыкании гранул между собой, что эквивалентно случаю сплошного металла, можно считать, что:

, , , (49)

откуда получаем:

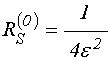. (50)

Полагая, что волна от сплошного металла отражается полностью, то есть , находим коэффициент . Подставляя это значение в (50), а также заменяя в соответствии с (11), окончательно получаем коэффициент отражения в виде:

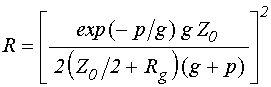. (51)

Из полученной формулы видно, что коэффициент отражения в таком виде не зависит от толщины пленки. Однако в экспериментах при увеличении толщины пленки коэффициент отражения всегда возрастает [27,28]. В формуле (51) так получилось из-за того, что пленка заведомо предполагалась состоящей из одного слоя гранул, имеющих кубическую форму, то есть толщина пленки равнялась размеру одной гранулы. Зависимость от толщины в формулу (51) можно ввести, если предположить, что сопротивление тем меньше, чем толщина пленки больше, например вводя замену:

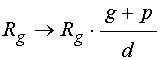, (52)

где – толщина пленки в целом.

При этом коэффициент отражения принимает вид:

. (53)

Представленный в таком виде коэффициент отражения при малой толщине пропорционален квадрату толщины, а при большой стремится к постоянному значению, близкому к единице. Такое его поведение находится в хорошем соответствии с экспериментами [27,28] и общими теоретическими положениями [43,44,51,52].

Можно видеть, что полученный коэффициент отражения от частоты волны никак не зависит, что является следствием решения задачи в условиях квазистационарности.

18. Численная оценка поля вторичной волны

Для численной оценки положим, что удельная проводимость материала гранулы с учетом аморфного характера составляет [27,28], то есть удельное сопротивление равно: . Приближенно полагая гранулу в виде куба с ребром равным 5 нм, находим ее сопротивление с помощью формулы [48,49]:

, (54)

где и – продольный размер и площадь поперечного сечения гранулы. Полагая , , получаем: .

Учитывая здесь, что [55], согласно (43), получаем поле вторичной волны:

. (55)

Таким образом, можно видеть, что рассматриваемый механизм внутригранулярных токов способен обеспечить поле отраженной волны по величине того же порядка, что и поле падающей волны.

19. Коэффициент отражения для кубических гранул

Для кубической гранулы, то есть при ; , из (54) получаем:

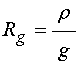. (56)

Подставляя (56) в (53), получаем коэффициент отражения:

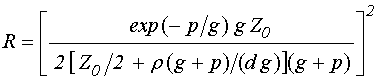, (57)

или подставляя:

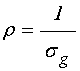, (58)

где – удельная проводимость материала гранулы, получаем:

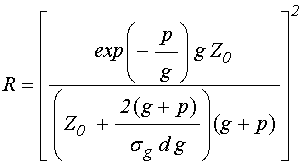. (59)

В реальных гранулированных пленках размеры гранул, как правило, значительно превышают размеры промежутков между ними, то есть приближенно можно положить: . При таком условии формула (59) допускает существенное упрощение:

. (60)

В соответствии с проведенным рассмотрением, полученные выражения (59) и (60) позволяют определить коэффициент отражения непосредственно вблизи поверхности пленки. Для получения амплитуд распространяющихся волн, надо решить электродинамическую задачу, содержащую условия распространения волн в средах, с обеих сторон примыкающих к пленке. В простейшем случае для этой цели можно эффективно использовать метод переотражений, описанный например в [56,57].

Замечание. В настоящем рассмотрении кубическая форма гранул и их расположение в виде правильной квадратной решетки выбраны для удобства проведения оценочного расчета. Учет сферической формы гранул в сочетании с их хаотическом расположением, по-видимому, может изменить полученный результат не более чем в разы, но не на порядки, то есть не меняет правомерности выполненной оценки по существу.

20. Коэффициент отражения при различной проводимости пленок

Рассмотрим теперь, как связан рассчитанный по описанной модели гранулярных токов коэффициент отражения с удельной проводимостью гранулированных пленок, исследованных в настоящей работе.

На рис.6 представлена зависимость коэффициента отражения от удельной проводимости пленок . Сплошные точки – результаты экспериментов по измерению коэффициента отражения и статической проводимости пленок. Открытые точки – те же результаты экспериментов, построенные при значении проводимости, увеличенной на два порядка по сравнению с измеренной на постоянном токе. Сплошная линия – результаты расчета по формуле (60) при толщине пленки . Точечная линия – результаты расчета по той же формуле при .

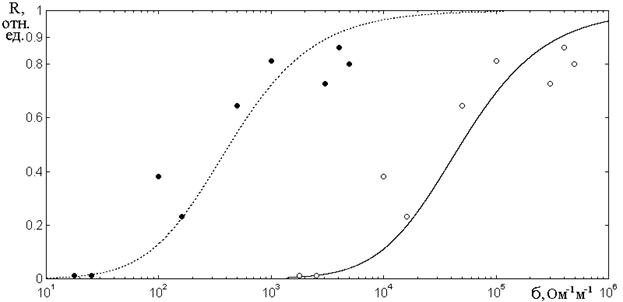
Рис.6. Зависимость коэффициента отражения от удельной проводимости пленок.

Из рис.6 видно, что реальные экспериментальные точки соответствуют точечной кривой, тогда как те же точки, сдвинутые по горизонтальной оси на два порядка соответствуют сплошной кривой. Это означает, что для того, чтобы результаты экспериментов по измерению коэффициента отражения соответствовали расчету по модели гранулярных токов, реально измеренная проводимость пленок должна быть увеличена на два порядка.

Такое обстоятельство становится понятным, если учесть, что модель гранулярных токов построена с учетом проводимости материала гранул , тогда как в экспериментах на постоянном токе измеряется средняя проводимость пленки , в формировании которой высокопроводящие гранулы перемежаются с низкопроводящими промежутками, в результате чего такая интегральная проводимость значительно снижается (то есть имеет место соотношение: ).

21. Формирование вторичных волн от двух поверхностей пленки

До этого места рассматривались создаваемые гранулярными токами волны, отходящие относительно слоя гранул только на одну какую-то сторону. Однако реальная пленка имеет две поверхности, каждая из которых создает свою совокупность вторичных волн, которые далее могут взаимодействовать друг с другом. Рассмотрим теперь образование проходящей и отраженной волн с учетом двух поверхностей пленки.

Рис.7. Схема образования полей волн, выходящих из пленки.

а – схема поперченного сечения пленки; б – поля вторичных волн вблизи поверхностей пленки; в – поля отраженной и проходящей волн.

Схема образования полей отраженной и проходящей волн иллюстрируется рис.7. На рис.7а показано поперечное сечение пленки. Как показано в разделе 14 (рис.4), активными в плане создания вторичных волн являются только поверхностные слои пленки, образованные одним рядом гранул. Два таких слоя, соответствующие противоположным поверхностям пленки, обозначены цифрами 1 и 2.

На пленку с левой стороны рисунка падает волна, поля которой обозначены и . Каждый из поверхностных слоев пленки создает две волны, распространяющиеся по нормали к плоскости пленки в противоположные стороны. Поля этих волн обозначены и .

На рис.7б показана схема пространственного распределения электрических полей волн, отходящих от поверхностей пленки в обе стороны.

В квазистационарном приближении задача о пространственном распределении электрического поля вторичной волны подобна задаче электростатики о поле бесконечно протяженной заряженной плоскости. Как известно [48,49], поле такой плоскости не зависит от расстояния до нее. Однако при ограниченных поперечных размерах плоскости поле спадает по закону, близкому к экспоненте, показатель которой пропорционален соотношению между пространственной протяженностью плоскости и расстоянием до нее.

Таким образом, будем считать, что поля вторичных волн направлены в противоположные стороны относительно друг друга и по мере удаления от создающего их поверхностного слоя пленки, подобным же образом монотонно спадают.

22. Влияние кластерного характера пленок

Будем полагать, что пленка по поверхности не является однородной, а представляет собой совокупность хорошо проводящих кластеров (зерен), разделенных плохо проводящими промежутками. Поперечный размер кластеров будем считать значительно превышающим размер гранул, то есть каждый кластер содержит большое количество более или менее равномерно распределенных гранул. Таким образом, можно полагать, что излучение вторичных волн происходит не со всей однородной поверхности пленки, а из совокупности кластерных областей, размер которых значительно превышает размер отдельной гранулы, однако имеет тот же порядок, что и толщина пленки.

Характер спада вторичной волны относительно поверхности пленки будет определяться соотношением между протяженностью кластерной области и размером гранулы, однако суммирование полей вторичных волн от обеих поверхностей пленки будет происходить различным образом в зависимости от соотношения между размером кластерной области и толщиной пленки.

Сказанное иллюстрируется рис.7в где показаны случаи суммирования для тонкой (слева) и толстой (справа) пленки. Здесь размер кластерной области обозначен через , а толщина пленки – по прежнему через . В случае тонкой пленки поля от противоположных поверхностей пленки взаимно проникают друг в друга, причем в результате их сложения из-за различия знаков поля выходящих волн взаимно почти компенсируются. В случае толстой пленки поля от противоположных поверхностей пленки не мешают друг другу, в результате чего остаются достаточно сильными. Таким образом, в случае тонкой пленки вторичные волны почти не образуются, тогда как в случае толстой – образуются в полной мере. При анализе интенсивностей отраженной и проходящей волн от пленки в целом следует учесть, что отраженная волна формируется за счет чисто вторичных волн, тогда как проходящая является сумой вторичной волны (с обратным знаком) с той частью падающей волны, которая проходит насквозь через пленку. Таким образом получаем, что от тонких пленок, удовлетворяющих условию отражается мало, а проходит много, в случае толстых пленок отражается много, но проходит мало.

Резюмируя сказанное, можно полагать, что существует какое-то критическое значение толщины пленки, по порядку близкое к величине кластерной области, начиная с которого отражение от пленки резко возрастает, а соответственно прохождение падает.

23. Зернистость пленок как проявление их кластерного характера

Для выяснения степени правдоподобия описанного механизма рассмотрим исследованные в настоящей работе пленки с точки зрения их кластерного характера.

Все исследовавшиеся в наших экспериментах пленки имели ярко выраженный зернистый характер, что отчетливо контролировалось с помощью атомного силового микроскопа. В таблице №2 приведены размеры зерен для пленок различных толщин. Промежутки между зернами составляли обычно примерно половину тех же расстояний.

Таблица №2.

Толщина (нм)	Размер зерен (нм)
70	33
190	37
320	70
400	79
550	95

Из таблицы видно, что размер зерен с увеличением толщины пленки увеличивается, причем отношение толщины пленки к размеру зерна, составляя от 2 до 5, тоже растет. Средний по всей таблице размер зерен составляет около 60 нм при средней толщине пленки около 300 нм. Таким образом, для исследуемых пленок размер зерен имеет тот же порядок, что и их толщина, поэтому можно полагать, что значение критической толщины пленок также должно быть того же порядка, то есть составлять 300 – 500 нм.

24. Влияние толщины пленок

Рассмотрим теперь, как зависит коэффициент отражения, рассчитанный по модели гранулярных токов, от толщины пленки.

Рис.8. Зависимость коэффициента отражения от толщины пленок при различных значениях проводимости материала гранул . Сплошные линии – теория, точки – результаты эксперимента.

1 – ; 2 – ; 3 – ;

4 – ; 5 – ; 6 – ; 7 – ; 8 – .

На рис.8 приведены зависимости коэффициента отражения от толщины пленок при различных значениях проводимости материала гранул . Теоретические кривые рассчитаны по формуле (60).

Из рис.8 видно, что при увеличении толщины коэффициент отражения возрастает тем сильнее, чем проводимость материала гранул больше. Экспериментальные точки приходятся на значения проводимости порядка , что довольно неплохо согласуется со значениями удельной проводимости для металлических пленок в аморфном состоянии [28] (например, для железа: [27,41,53,54]).

Однако в эксперименте зависимость коэффициента отражения от толщины носит резко немонотонный характер, а именно: до толщины порядка 400 нм отражение практически отсутствует, после чего в интервале от 400 до 600 нм резко возрастает, достигая значений 0.8 и более.

Такое резко скачкообразное увеличение коэффициента отражения от нуля почти до единицы в довольно узком интервале толщин, по-видимому, говорит как раз о достижении в этом интервале критического значения толщины, рассмотренного в предыдущем разделе, по-видимому, близкого к 400 нм. То есть ниже этого значения отраженная волна практически компенсируется вторичными волнами от двух поверхностей пленки, тогда как выше – компенсация нарушается и отражение от каждой из поверхностей принимает независимый характер. При этом волна, отраженная от более удаленной поверхности пленки, на ее толщине практически спадает до нуля, оставляя нетронутой волну, отраженную от ближайшей поверхности пленки.

25. Интерпретация результатов эксперимента с учетом компенсации вторичных волн

Роль механизма компенсации вторичных волн иллюстрируется рис.9, где показана та же зависимость коэффициента отражения от толщины пленок.

Из предыдущего рис.8 можно видеть, что более или менее соответствующее эксперименту скачкообразное изменения коэффициента отражения с толщиной можно обеспечить только при значении удельной проводимости материала гранул равном (кривая 8 на рис.8). Однако такое отражение реализуется только при достижении толщиной критического значения порядка 400 нм. Поэтому приведенная на рис.9 кривая, построенная по формуле (60), сдвинута по горизонтальной оси как раз на эту величину. Видно, что теперь согласие теории с экспериментом носит вполне удовлетворительный характер.

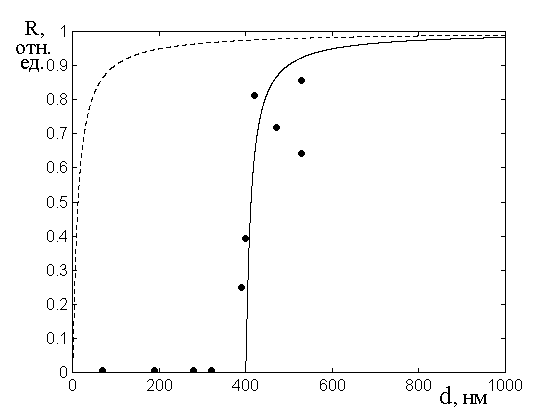
Рис.9. Зависимость коэффициента отражения от толщины пленок с учетом компенсации вторичных волн. Сплошная линия – теория с учетом компенсации, пунктир – без учета компенсации. Точки – результаты эксперимента. Проводимость – .

Заметим однако, что произведенный здесь сдвиг теоретической кривой носит, хотя и правдоподобный, но все же довольно произвольный характер, то есть годится лишь для оценки. Для большей корректности оценки роли компенсации вторичных волн надо реально определить крутизну спада поля вторичных волн по нормали к плоскости пленки с учетом размера кластеров, что требует более подробного исследования.

Заключение

Основные результаты настоящей работы сводятся к следующему.

Экспериментально исследована статическая проводимость и отражение электромагнитных волн от тонких пленок гранулированных аморфных металл-диэлектрических нанокомпозитов в широком диапазоне концентраций металлической фазы. Показано, что статическая проводимость пленок с увеличением концентрации проводящей фазы увеличивается. Энергетический коэффициент отражения волны СВЧ от пленок, при малых концентрациях будучи незначительным, резко возрастает вплоть до единицы при концентрациях порядка , что обусловлено переходом от диэлектрического типа распространения волны к металлическому.

Показано, что динамическая проводимость в диапазоне СВЧ превышает статическую, измеренную на постоянном токе, на два-четыре порядка, принимая такие значения задолго до порога перколяции металлической фазы, причем степень превышения в диапазоне частот до 40 ГГц от частоты не зависит.

Для объяснения наблюдаемого в экспериментах частотнонезависимого превышения эффективной динамической проводимости над статической предложен механизм внутригранулярных (внутрикластерных) токов. Предложена модель планарного распределения гранул внутри пленки, на основе которой показано, что в диапазоне частот, на которых проводились эксперименты, поля вторичных волн, создаваемых волной, падающей на слой гранул, могут приближаться по величине к полю падающей волны.

На основе предложенной модели рассчитан коэффициент отражения волны от одного слоя гранул. В формировании вторичных волн выявлена определяющая роль поверхностных слоев гранул, обусловленная взаимной компенсацией полей соседствующих гранул.

Модель обобщена на случай пленки, содержащей значительное количество слоев. Рассмотрены особенности формирования отраженной и проходящей волн в предельных случаях тонкой и толстой пленки.

Результаты расчета по предложенной модели сопоставлены с экспериментами по отражению волн от пленок. Выявлено хорошее соответствие как по порядку величины коэффициента отражения, так и по связи его с толщиной пленок. Результаты эксперимента интерпретированы с учетом механизма компенсации вторичных волн. Предсказано и выявлено в эксперименте существование критического значения толщины пленки, определяющего порог резкого роста коэффициента отражения, обусловленного механизмом раскомпенсации.

Даны рекомендации для дальнейших исследований, в том числе более подробного выявления структурного характера пленок, а также механизмов формирования вторичных волн с учетом многослойной структуры и взаимной компенсации волн от отдельных слоев гранул.

Работа выполнена при финансовой поддержке РФФИ (гранты №12-02-01035-а, №13-02-01401-а).

Литература

1. Суздалев И.П. Нанотехнология. Физико-химия нанокластеров, наноструктур и наноматериалов. М.: КомКнига. 2006.

2. Рит М. Наноконструирование в науке и технике. Введение в мир нанорасчета. Москва-Ижевск: НИЦ "Регулярная и хаотическая динамика". 2005.

3. Neugebauer C.A. // Thin Solid Films. 1970. V.6. P.443.

4. Gittleman J.L., Goldstain Y., Bozowski S. // Phys.Rev.B. 1972. V.5. P.3609.

5. Калинин Ю.Е., Ремизов А.Н., Ситников А.В. // ФТТ. 2004. Т.46. №11. С.2076.

6. Kotov L.N., Turkov V.K., Vlasov V.S., Kalinin Yu.E., Sitnikov A.V. // Mat.Sci.Eng. 2006.V.442. P.352.

7. Вендик И.Б., Вендик О.Г. // ЖТФ. 2013. T.83. №1. С.3.

8. Parimi P.V., Lu W.T., Vodo P., Sokoloff J., Derov J.S., Sridhar S. // Phys. Rev. Lett. 2004. V.92. №12. P.127401(4).

9. Гуляев Ю.В., Никитов С.А., Животовский Л.В., Климов А.А., Тайад Ф., Пресманес Л., Бонин К., Цай Ч.С, Высоцкий С.Л., Филимонов Ю.А. // Письма в ЖЭТФ. 2003. T.77. №10. C.670.

10. Веселаго В.Г. // УФН. 1967. T.92. №3. C.517.

11. Агранович В.М., Гартштейн Ю.Н. // УФН. 2006. T.176. №10. C.1052.

12. Петров Ю.И. Кластеры и малые частицы. М.: Наука. 1986.

13. Gerber A., Milner A., Groisman B. et al. // Phys. Rev. B. 1997. V.55. №10. P.6446.

14. Казанцева Н.Е., Пономаренко А.Т., Шевченко В.Г., Чмутин И.А., Калинин Ю.Е., Ситников А.В. // Физика и химия обработки материалов. 2002. №1. C.5.

15. Kotov L.N., Efimets Yu.Yu., Vlasov V.S., Petrakov A.P., Turkov V.K., Kalinin Yu.E., Sitnikov A.V. // Adv.Mat.Rep. 2008. V.47-50. Pt.1. P.706.

16. Иванов А.В., Калинин Ю.Е., Нечаев А.В., Ситников А.В.//ФТТ. 2009. Т.51. №12. С.2331.

17. Sheng P., Abeles B., Arie Y. // Phys.Rev.Lett. 1973. V.31. №1. P.44.

18. Мейлихов Е.З. // ЖЭТФ. 1999. Т.115. №4. С.1484.

19. Abeles B., Cohen R.W., Cullen G.W. // Phys.Rev.Lett. 1966. V.17. №4. P.632.

20. Cuevas E., Ortuno M., Ruiz J. // Phys.Rev.Lett. 1993. V.71. №12. P.1871.

21. Луцев Л.В., Звонарева Т.К., Лебедев В.М. // Письма в ЖТФ. 2001. Т.27. №15. С.84.

22. Луцев Л.В., Калинин Ю.Е., Ситников А.В., Стогней О.В. // ФТТ. 2002. Т.44. №10. С.1802.

23. Луцев Л.В. // ФТТ. 2002. Т.44. №6. С.97.

24. Lutsev L.V., Yakovlev S.V. // J.Appl.Phys. 1998. V.83. №11. P.7330.

25. Луцев Л.В., Яковлев С.В. // Сб.тр. XVII Международной школы-семинара «Новые магнитные материалы микроэлектроники». 2000. М.:УРСС-МГУ. С.254.

26. Луцев Л.В., Яковлев С.В., Сиклицкий В.И. // ФТТ. 2000. Т.42. №6. С.1105.

27. Антонец И.В., Котов Л.Н., Некипелов С.В., Шавров В.Г., Щеглов В.И. // РЭ. 2004. Т.49. №10. 1243.

28. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2006. Т.51. №12. С.1481.

29. Власов В.С., Гущин Н.Н., Котов Л.Н., Калинин Ю.Е., Ситников А.В., Шавров В.Г., Щеглов В.И. // Сб. тр. XIX Международной конференции «Электромагнитное поле и материалы». 2011. М.: НИУ МЭИ. С.194.

30. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2014. Т.59. №7. В печати.

31. Калинин Ю.Е., Котов Л.Н., Петрунёв С.Н., Ситников А.В. // Изв.РАН. Сер.физич. 2005. Т.69. №8. С.1195.

32. Антонец И.В., Котов Л.Н., Калинин Ю.Е., Ситников А.В., Шавров В.Г., Щеглов В.И. // ПЖТФ. 2014. Т.40. №14. С.1.

33. Калинин Ю.Е., Пономаренко А.Т., Ситников А.В., Стогней О.В. // Физика и химия обработки материалов. 2001. №5. С.14.

34. Ситников А.В. Электрические и магнитные свойства наногетерогенных систем металл-диэлектрик. Диссертация на соискание ученой степени докт. физ.-мат. наук. Воронеж: ВГТУ. 2010. 318 с.

35. Kalinin Yu.E., Sitnikov A.V., Stognei O.V., Zolotukhin I.V., Neretin P.V. // Mat. Scien. and Engin. 2001. A304-306. P.941.

36. Золотухин И.В., Неретин П.В., Калинин Ю.Е., Стогней О.В., Ситников А.В. // Альтернативная энергетика и экология. 2002. №2. С.7.

37. Калинин Ю.Е., Пономаренко А.Т., Ситников А.В., Стогней О.В. // Физика и химия обработки материалов. 2002. №5. С.14.

38. Ohnuma M., Hono K., Abe T. et al. // J. Appl. Phys. 1997. V.82. №11. P.5646.

39. Калинин Ю.Е., Пономаренко А.Т., Ситников А.В., Стогней О.В. // Инженерная физика. 2003. №5. С.44.

40. Татаринова Л.И., Структура твердых аморфных и жидких веществ. М.: Наука. 1983.

41. Антонец И.В., Котов Л.Н., Некипелов С.В., Голубев Е.А. // ЖТФ. 2004. Т.74. №3. С.24.

42. Гороновский И.Т., Назаренко Ю.П., Некряч Е.Ф. Краткий справочник по химии. Киев: Наукова думка. 1974.

43. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. //

РЭ. 2007. Т.52. №4. С.403.

44. Антонец И.В., Щеглов В.И. Распространение волн через тонкие слои и пленки. Сыктывкар: ИПО СыктГУ. 2010.

45. Каплан А.Е. // РЭ. 1964. Т.9. №10. С.1781.

46. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2008. Т.53. №8. С.901.

47. Левич В.Г. Курс теоретической физики. Т.1. М.: Наука. 1969.

48. Калашников С.Г. Электричество. М.: Наука. 1964.

49. Сивухин Д.В. Общий курс физики. Т.3. Электричество.

М., Наука, 1977.

50. Двайт Г.Б. Таблицы интегралов и другие математические формулы. М.: Наука. 1973.

51. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. //

РЭ. 2010. Т.55. №2. С.133.

52. Антонец И.В., Щеглов В.И. Распространение волн через многослойные структуры (монография). Часть первая. Прямой метод. Сыктывкар: ИПО СыктГУ. 2011.

53. Антонец И.В., Котов Л.Н., Некипелов С.В., Шавров В.Г., Щеглов В.И. // Proc. XII Intern. Conference on Spin-Electronics and Gyrovector Electrodynamics, Moscow (Firsanovka). 2003. Publ.UNC-1 MPEI (TU). Р.642.

54. Антонец И.В., Котов Л.Н., Некипелов С.В., Карпушов Е.Н. // ЖТФ. 2004. Т.74. №11. С.102.

55. Чертов А.Г. Единицы физических величин. М.: Высшая школа. 1977.

56. Борн М., Вольф Э. Основы оптики. М.: Наука. 1970.

57. Антонец И.В., Щеглов В.И. Распространение волн через многослойные структуры (монография). Часть четвертая. Специфические методы. Сыктывкар: ИПО СыктГУ. 2013.