УДК 621.391
ПРОГНОЗИРОВАНИЕ ДОСТОВЕРНОСТИ ПРИЕМА ОФМ СИГНАЛОВ ДЛЯ ПОТЕНЦИАЛЬНО ВОЗМОЖНЫХ РЕЖИМОВ РАБОТЫ
В. В. Егоров, М. С. Смаль
ОАО «Российский институт мощного радиостроения, Санкт-Петербург
Статья получена 1 апреля 2013 г.
Аннотация. Рассмотрены способы прогнозирования вероятности ошибки на бит для сигналов с относительной фазовой модуляцией повышенной позиционности на основе анализа сигналов с заданной позиционностью модуляции, показана возможность их применения для адаптивных систем передачи данных.
Ключевые слова: вероятность ошибки на бит, канал связи, прогнозирование качества канала, передача данных.
Abstract: Methods of bit error probability forecast for signals with higher phase modulation type that is based on signal analysis with definite phase modulation type. Possibility of its application for adaptive data communication systems.
Key words: bit error probability, communication channel, channel quality forecast, data communications.
При передаче информации по нестационарным радиоканалам, характеризующимся замираниями огибающей сигнала, широко используются адаптивные системы передачи сообщений. В этих условиях наиболее подходящими являются сигналы с относительной фазовой модуляцией (ОФМ) различной позиционности, для демодуляции которых не требуется знания амплитуды и начальной фазы несущего колебания. Наиболее часто адаптация заключается в выборе оптимальной позиционности модуляции, критерием выбора которой является максимум скорости передачи при заданной допустимой вероятности ошибки на бит.
Выбор оптимального вида модуляции ОФМ сигналов осуществляется обычно путём прерывания потока полезной информации и посылки тестовых сигналов соответствующего вида [1], [2]. Однако, для обеспечения максимальной эффективности работы систем желательно применять подходы, которые позволяют сформировать оценки, необходимые для принятия решения по информационному сигналу, без использования какой-либо избыточности. Поэтому актуальной является задача прогнозирования достоверности приёма сигналов ОФМ различной позиционности непосредственно в процессе приёма информационных сигналов.
Как известно, одним из самых помехоустойчивых режимов передачи является двухпозиционная относительная фазовая модуляция (ОФМ-2). Именно такой вид модуляции обычно используется в начале сеанса связи. В этом случае оценить вероятность ошибки на бит при использовании ОФМ более высокой позиционности можно на основе следующего подхода.
Рассмотрим задачу оценки вероятности ошибки на бит для сигналов с четырехпозиционной относительной фазовой модуляцией (ОФМ-4). Передача символов 0 и 1 для сигналов ОФМ-2 эквивалентна передаче символов 00 и 11 для сигналов с ОФМ-4. Тогда вероятность ошибки на бит для сигналов с ОФМ-4 связана с вероятностью попадания фазы принятого сигнала в сектора, соответствующие символам 00 и 11, с учетом расстановки фаз в соответствии с кодом Грея, описывается следующим уравнением:
|
|
(1) |
где ![]() – вероятность события, состоящего в
том, что фаза принятого сигнала оказалась в секторах, соответствующих символам
00 или 11, независимо от того, какой символ передавался,
– вероятность события, состоящего в
том, что фаза принятого сигнала оказалась в секторах, соответствующих символам
00 или 11, независимо от того, какой символ передавался, ![]() – вероятность ошибки на бит для
сигналов с ОФМ-4.
– вероятность ошибки на бит для
сигналов с ОФМ-4.
В качестве оценки ![]() можно использовать соответствующую
частость, доступную для измерения:
можно использовать соответствующую
частость, доступную для измерения:
|
|
(2) |
где ![]() – количество попаданий фазы
принятого сигнала в сектора, соответствующие символам 00 и 11,
– количество попаданий фазы
принятого сигнала в сектора, соответствующие символам 00 и 11, ![]() – объем выборки. При такой замене следует учитывать,
что решением нового уравнения будет уже не истинная, а оценка вероятности
ошибки на бит
– объем выборки. При такой замене следует учитывать,
что решением нового уравнения будет уже не истинная, а оценка вероятности
ошибки на бит ![]() , которая характеризуется
погрешностью.
, которая характеризуется
погрешностью.
Таким образом, в достаточно простой вычислительной схеме можно получить оценку вероятности ошибки на бит для сигналов с ОФМ-4 во время приема полезной информации, передаваемой с помощью сигналов с ОФМ-2. При этом получаемая оценка, как показывает вычислительный эксперимент, является несмещенной.
Получение оценки вероятности ошибки на бит для сигналов с восьмипозиционной относительной фазовой модуляцией (ОФМ-8) при передаче сообщения сигналами с ОФМ-2 осуществляется аналогичным образом. Для этого символам 0 и 1 в соответствии с кодом Грея сопоставляются символы 000 и 110. Тогда уравнение для вероятности ошибки на бит в режиме ОФМ-8 имеет вид:
|
|
(3) |
где ![]() – количество попаданий фазы
принятого сигнала в сектора, соответствующие символам 000 или 110.
– количество попаданий фазы
принятого сигнала в сектора, соответствующие символам 000 или 110.
Также можно получить уравнение для ожидаемой вероятности ошибки на бит для сигналов с шестнадцатипозиционной относительной фазовой модуляцией (ОФМ-16) при передаче сообщения сигналами с ОФМ-2. Для этого символам 0 и 1 в соответствии с кодом Грея сопоставляются символы 0000 и 1100. Тогда уравнение для вероятности ошибки на бит в режиме ОФМ-16 имеет вид:
|
|
(4) |
где ![]() – количество попаданий фазы
принятого сигнала в сектора, соответствующие символам 0000 или 1100.
– количество попаданий фазы
принятого сигнала в сектора, соответствующие символам 0000 или 1100.
Аналогично удается получить уравнение для ожидаемой вероятности ошибки на бит в режиме ОФМ-8 и ОФМ-16 при передаче информации сигналами с ОФМ-4:
|
|
(5) |
где ![]() – количество попаданий фазы
принятого сигнала в сектора, соответствующие символам 000, 110, 101 или 011,
– количество попаданий фазы
принятого сигнала в сектора, соответствующие символам 000, 110, 101 или 011,
|
|
(6) |
где ![]() – количество попаданий фазы
принятого сигнала в сектора, соответствующие символам 0000, 0110, 1100 или
1010.
– количество попаданий фазы
принятого сигнала в сектора, соответствующие символам 0000, 0110, 1100 или
1010.
Точно также удается получить уравнение для ожидаемой вероятности ошибки на бит в режиме ОФМ-16 при передаче информации сигналами с ОФМ-8:
|
|
(7) |
где ![]() – количество попаданий фазы
принятого сигнала в сектора, соответствующие символам 0000, 0011, 1100, 1010,
0110, 0101, 1100 или 1111.
– количество попаданий фазы
принятого сигнала в сектора, соответствующие символам 0000, 0011, 1100, 1010,
0110, 0101, 1100 или 1111.
Полученные уравнения являются нелинейными и для степеней выше 2 должны решаться численными методами. При этом, объём выборки порядка 104, который можно получить для сигналов в полосе телефонного канала за время порядка 2-8 с, позволяет сделать определяемую частотность достаточно близкой к истинной вероятности ошибки на бит, что значительно уменьшает погрешность оценки.
Зависимости вероятностей попадания в соответствующие сектора вычисленных значений разности фаз принятого сигнала с текущей модуляцией от вероятности ошибки на бит для модуляции повышенной позиционности приведены на рисунке 1.
Следует также отметить, что решения всех уравнений являются устойчивыми в интересной для практики области оцениваемых вероятностей для нестационарного радиоканала в диапазоне [0,01-0,1], так как значительным отклонениям доступной для измерения частости событий, входящих в правую часть уравнений, соответствуют незначительные отклонения оцениваемых вероятностей ошибки на бит от истинных значений.
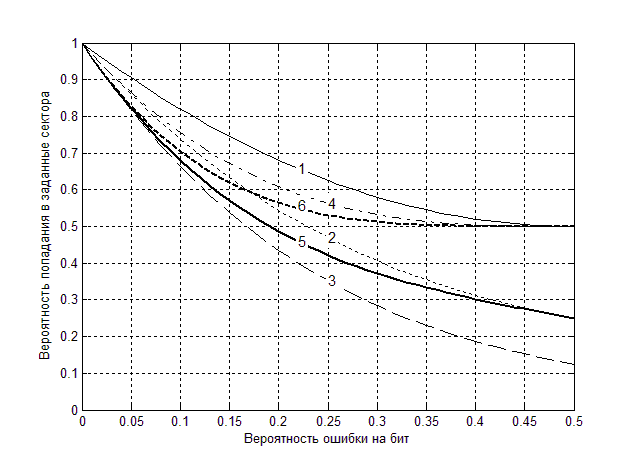
Рисунок 1. Зависимости вероятностей попадания в заданные сектора от вероятности ошибки на бит в канале связи.
1– для ОФМ-4 при ОФМ-2
2– для ОФМ-8 при ОФМ-2
3– для ОФМ-16 при ОФМ-2
4– для ОФМ-8 при ОФМ-4
5– для ОФМ-16 при ОФМ-4
6– для ОФМ-16 при ОФМ-8
После получения оценок вероятностей ошибки на бит для всех используемых в системе передачи данных сигналов, выбирается та позиционность ОФМ, которая позволяет обеспечить максимальную информационную скорость при допустимом уровне вероятности ошибки на бит. Таким образом, используя данный подход, можно выбрать наиболее оптимальный режим функционирования системы передачи данных в любой момент времени. Для получения оценки, которая является несмещенной, используется достаточно простой алгоритм, не требующий больших вычислительных затрат. При этом оценка формируется в результате анализа информационного сигнала и полностью отсутствует необходимость передавать дополнительные тестовые сигналы, что позволяет повысить информационную скорость передачи данных, а также позволяет сделать вывод, что зондирование канала в процессе передачи информации является заведомо излишней операцией для указанных целей.
1. Митряев Е. В., Ростовцев Ю. Г., Рышков Ю. П. Контроль верности информации в морской радиосвязи. — Л. : Судостроение, 1979.
2. Коричнев Л. П., Королев В. Д. Статистический контроль каналов связи. — М. : Радио и связь, 1989.