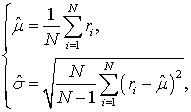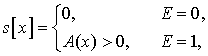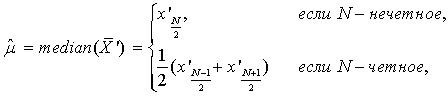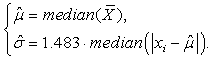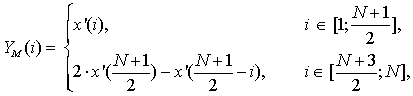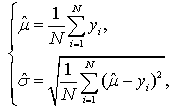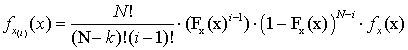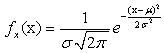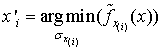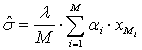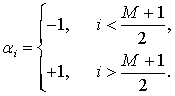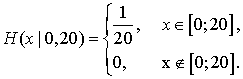МЕТОД ОЦЕНКИ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ ГАУССОВСКОГО ШУМА ДЛЯ ЗАДАЧ ОБНАРУЖЕНИЯ ИМПУЛЬСНОГО СИГНАЛА
И. С. Осадчий
Научно-производственное объединение «Лептон»
Статья получена 24 марта 2015 г.
Аннотация. Работа посвящена задаче точечной оценки параметров сдвига и масштаба функции распределения аддитивного гауссовского шума при обнаружении на его фоне некогерентной последовательности однополярных импульсов. Произведен анализ данной задачи, показывающий её схожесть с задачей оценки параметров распределения случайной величины по набору её реализацией при засорении выборки. Рассмотрены некоторые из основных методов решений, применение которых возможно в составе автоматизированных вычислительных систем обнаружения, производящих обработку данных в режиме реального времени. Предложен метод устойчивой оценки, состоящий из двух шагов: шага усечения выборки и шага вычисления оценок параметров. Произведено исследование и сравнительный анализ значений эффективности и устойчивости оценок, полученных с помощью рассмотренных и предложенного методов.
Ключевые слова: задача обнаружения; импульсный сигнал; методы устойчивой оценки.
Abstract. In this article the problem of estimation of mean and variance parameters of additive Gaussian noise for detection of non-coherent pulse signal is described. Analysis of this problem revealed that it is similar to the robust statistics task of estimate of data with outliers. Some of the popular methods that can be implemented for digital real-time data processing were described. New method of parameters estimate was offered. It consists of two steps: removal of outliers and robust estimation. Research and comparative analysis of effectiveness and stability of estimation for different methods is done.
Key words: problem of signal detection; pulse signal; robust estimation.
Введение
Для многих современных цифровых устройств характерна ситуация, при которой принимаемый сигнал представляет собой смесь некогерентной последовательности однополярных импульсов [1], содержащих целевую информацию, и аддитивного гауссовского шума, возникающего за счет физической природы передачи сигнала [2]. При этом параметры функции распределения шумовой составляющей являются неизвестными и подвержены изменениям в процессе передачи данных. Например, такая ситуация возможна в системах радиолокации [3], где амплитуды импульсов пропорциональны расстояниям до объектов, в аналоговых телевизионных системах, в которых импульсами кодируются синхронизирующие сигналы [4], и в системах обработки данных в оптико-электронных приборах, целевой информацией которых являются точечные объекты на монотонном изображении [5].
В зависимости от конечной цели, задача обнаружения импульсного сигнала может быть решена с помощью средств оптимального приема [6] при использовании критериев Байеса, минимизирующего средний риск [7], или критерия Неймана-Пирсона, фиксирующего вероятность одной из ошибок обнаружения [8]. Однако вне зависимости от выбора критерия существует необходимость в априорной информации относительно вероятностной модели шумовой составляющей. Поскольку она исходно имеет нормальный закон распределения, то может быть полностью описана параметрами математического ожидания (сдвига) и среднеквадратичного отклонения (масштаба) [9].
Классическим подходом для получения оценок данных параметров является использование методов максимального правдоподобия по выборке отсчетов принимаемого сигнала:
|
(1) |
где ![]() –
оценка параметра сдвига,
–
оценка параметра сдвига, ![]() – оценка параметра масштаба,
– оценка параметра масштаба,
![]() – отсчет входного сигнала,
– отсчет входного сигнала, ![]() – общее количество элементов.
– общее количество элементов.
Однако при наличии однополярных импульсов в выборке
получаемые таким методом оценки будут смещены, что может привести как к пропуску
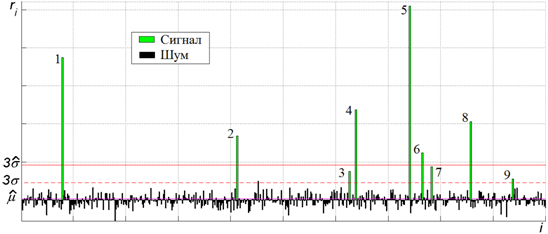
целевой информации, так и к неверному измерению амплитуд. На Рисунке 1
представлен пример набора отсчетов входного сигнала ![]() ,
содержащего девять сигнальных импульсов, и обозначены полученные с помощью (1) значения
параметров сдвига и масштаба.
,
содержащего девять сигнальных импульсов, и обозначены полученные с помощью (1) значения
параметров сдвига и масштаба.
|
|
|
Рисунок 1. Смешение оценки параметров сдвига и масштаба |
Из представленного рисунка видно, что получаемая оценка
параметра масштаба (![]() ) сильно завышена относительно
истинного значения (
) сильно завышена относительно
истинного значения (![]() ), что приведет к пропуску при
обнаружении. Оценка параметра сдвига (
), что приведет к пропуску при
обнаружении. Оценка параметра сдвига (![]() ) также
является несколько завышенной, что исказит конечное измерение амплитуд для
правильно обнаруженных сигнальных импульсов.
) также
является несколько завышенной, что исказит конечное измерение амплитуд для
правильно обнаруженных сигнальных импульсов.
В результате для снижения вероятностей ошибок обнаружения и измерения амплитуд необходимо применение иных методов оценки параметров распределения шумовой составляющей, позволяющих получить точечные значения более адекватные истинным. При этом данные методы должны быть реализованы в составе цифровых вычислительных устройств и иметь возможность обработки поступающего сигнала в режиме реального времени.
Постановка задачи
Принимаемый дискретный сигнал ![]() представляет
собой смесь недетерминированной помехи в виде аддитивного гауссовского шума
представляет
собой смесь недетерминированной помехи в виде аддитивного гауссовского шума ![]() и полезного импульсного сигнала
и полезного импульсного сигнала ![]() :
:
|
|
|
Значения шумовой составляющей ![]() описываются
плотностью вероятности нормального распределения с параметрами математического
ожидания
описываются
плотностью вероятности нормального распределения с параметрами математического
ожидания ![]() и среднеквадратичного отклонения
и среднеквадратичного отклонения ![]() :
:
|
(2) |
Характер возникновения однополярного импульсного сигнала ![]() является вероятностным и может быть
описан как:
является вероятностным и может быть
описан как:
|
(3) |
где ![]() –
значения сигнала при его наличии,
–
значения сигнала при его наличии, ![]() – случайная величина, определяющая
возникновение сигнала и подчиняющаяся закону распределения Бернулли с заданной вероятностью
– случайная величина, определяющая
возникновение сигнала и подчиняющаяся закону распределения Бернулли с заданной вероятностью
![]() .
.
По принимаемому набору отсчетов сигнала ![]() требуется получить векторную оценку
требуется получить векторную оценку ![]() параметров распределения шумовой
составляющей (2). При этом получаемая оценка должна удовлетворять ряду свойств [10].
параметров распределения шумовой
составляющей (2). При этом получаемая оценка должна удовлетворять ряду свойств [10].
Во-первых, она должна являться состоятельной [9], то есть сходиться по вероятности к истинному значению при увеличении объема выборки:
|
(4) |
где ![]() –
вектор истинных значений параметров,
–
вектор истинных значений параметров, ![]() – объем выборки,
– объем выборки, ![]() – бесконечно малая величина. Поскольку
– бесконечно малая величина. Поскольку ![]() является векторной, то требуется выполнение
свойства состоятельности для её компонент отдельно.
является векторной, то требуется выполнение
свойства состоятельности для её компонент отдельно.
Во-вторых, она должна являться несмещенной [11], то есть её математическое ожидание должно совпадать с истинным значением:
|
(5) |
при этом, так же, как и для
состоятельности, данному свойству должны удовлетворять все компоненты ![]() по отдельности.
по отдельности.
В случае, если выполнены оба предыдущих условия, то для
сравнения оценок, получаемых различными методами, можно пользоваться значением
эффективности [12]. Оно определяется как предел отношения ковариаций получаемой
оценки ![]() к эффективной оценке
к эффективной оценке ![]() при увеличении объема выборки:
при увеличении объема выборки:
|
(6) |
Доказано [13], что свойством эффективности для (2) обладают
оценки максимального правдоподобия. Остальные оценки считаются тем эффективнее,
чем больше значение ![]() .
.
Влияние, оказываемое на конечные значения векторной оценки ![]() наличием в выборке импульсного сигнала,
можно измерять как расстояние между положениями истинных значений параметров и
центром разброса полученных для них оценок:
наличием в выборке импульсного сигнала,
можно измерять как расстояние между положениями истинных значений параметров и
центром разброса полученных для них оценок:
|
(7) |
Поскольку применение вычисляемых значений параметров шумовой составляющей будет производиться в составе цифровых вычислительных устройств, решающих задачу обнаружения сигнала, то немаловажным критерием для выбора того или иного метода оценки является его вычислительная сложность. Данную характеристику можно рассматривать как совокупное количество элементарных вычислительных операций различного типа, требующихся для получения конечного результата.
Анализ задачи
Поставленная задача по своей сути схожа с классической задачей
робастной статистики [14], заключающейся в оценке параметров нормального
распределения по выборке, в которой присутствуют аномальные значения
(засорения). В данной задаче рассматривается набор реализаций ![]() случайной величины
случайной величины ![]() , функция распределения которой
описывается моделью Тьюки-Хьюбера:
, функция распределения которой
описывается моделью Тьюки-Хьюбера:
|
(8) |
где ![]() –
нормальный закон распределения (2),
–
нормальный закон распределения (2), ![]() – неизвестная функция
распределения засорения,
– неизвестная функция
распределения засорения, ![]() – процент засорения.
– процент засорения.
Применимо к поставленной задаче отсчеты поступающего сигнала
![]() можно рассматривать как набор реализаций
случайной величины
можно рассматривать как набор реализаций
случайной величины ![]() , подчиняющейся закону
распределения аддитивного гауссовского шума
, подчиняющейся закону
распределения аддитивного гауссовского шума ![]() . В
свою очередь, значения импульсного сигнала
. В
свою очередь, значения импульсного сигнала ![]() могут
быть рассмотрены как выбросы, подчиняющиеся
могут
быть рассмотрены как выбросы, подчиняющиеся ![]() , а
априорная вероятность появления сигнала
, а
априорная вероятность появления сигнала ![]() (3) представляет
собой процент засорения выборки.
(3) представляет
собой процент засорения выборки.
Однако поскольку сигнал ![]() является
набором однополярных импульсов, то
является
набором однополярных импульсов, то ![]() и выбросы такого
характера являются только правосторонними [15], то есть их наличие будет искажать правый хвост гистограммы распределения
и выбросы такого
характера являются только правосторонними [15], то есть их наличие будет искажать правый хвост гистограммы распределения ![]() . Это является отличием от модели
Тьюки-Хьюбера, в которой предполагается, что
. Это является отличием от модели
Тьюки-Хьюбера, в которой предполагается, что ![]() симметрично
относительно
симметрично
относительно ![]() и создает как правостороннее, так и
левостороннее засорение.
и создает как правостороннее, так и
левостороннее засорение.
Существующие решения
Одним из наиболее часто применяемых методов решения
поставленной задачи является метод Median Absolute Deviation (MAD, Медиана абсолютного отклонения) [16]. На Рисунке
2 представлена последовательность действий, которая необходима для получения
значения оценок математического ожидания ![]() и
среднеквадратичного отклонения
и
среднеквадратичного отклонения ![]() распределения по
выборке реализаций
распределения по
выборке реализаций ![]() в соответствии с данным методом.
в соответствии с данным методом.
|
|
|
Рисунок 2. Схема действий метода MAD |
Первым действием, производимым в рамках данного метода,
является сортировка поступающих отсчетов из ![]() , после
которой формируется упорядоченный набор:
, после
которой формируется упорядоченный набор:
|
(9) |
где ![]() – объем
как исходной выборки
– объем
как исходной выборки ![]() , так и сформированной выборки
, так и сформированной выборки ![]() .
.
Для получения оценки математического ожидания используется
медиана [17], то есть центральный элемент ранжированного множества ![]() , если N –
нечетное число или полусумма двух её центральных элементов, если N – четное число:
, если N –
нечетное число или полусумма двух её центральных элементов, если N – четное число:
|
(10) |
где ![]() ,
, ![]() и
и ![]() –
элементы из множества
–
элементы из множества ![]() .
.
Все последующие действия данного метода направлены на
получение устойчивой оценки среднеквадратичного отклонения ![]() . Сначала формируется множество
. Сначала формируется множество ![]() абсолютных отклонений элементов выборки
абсолютных отклонений элементов выборки ![]() от полученного значения математического
ожидания
от полученного значения математического
ожидания ![]() :
:
|
(11) |
Затем из полученных отклонений формируется ранжированный по возрастанию или убываю ряд:
|
(12) |
и конечное значение оценки ![]() получается в соответствии с выражением:
получается в соответствии с выражением:
|
(13) |
где коэффициент 1.483 используется для коррекции смещения (5).
В результате, исходя из (9) – (13), получение требующихся оценок параметров распределения по наблюдаемому множеству элементов выборки можно записать как:
|
(14) |
Главным достоинством данного метода является устойчивость получаемых оценок к засорению с обеих сторон, что, однако, является избыточным для поставленной задачи. Также немаловажными достоинствами являются простота реализации и высокая надежность метода, которые заключаются в детерминированной последовательности действий. Основную вычислительную сложность составляют процессы получения медиан, для которых существуют как различные способы аппаратного построения [18,19], так и множество программных алгоритмов [20].
Недостатком данного метода является низкая эффективность получаемых оценок. Для её повышения предлагаются различные варианты усовершенствований [21], однако, как правило, они сопряжены со значительным усложнением, что делает их трудно применимыми для обработки данных в режиме реального времени в составе автоматизированных систем обнаружения.
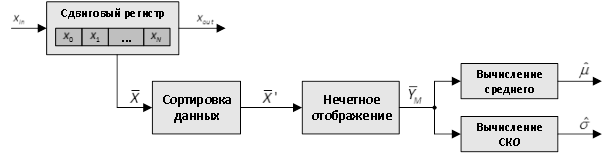
Другим методом решения поставленной задачи является метод Нечетного отображения выборки (НОВ), который был предложен в [22]. Основные действия данного метода и их последовательность, выраженные в виде структурной схемы, представлены на Рисунке 3.
|
|
|
Рисунок 3. Структурная схема метода нечетного отображения |
Для формирования набора данных ![]() используется
сдвиговый регистр, в котором хранится N
последних поступающих отсчетов
используется
сдвиговый регистр, в котором хранится N
последних поступающих отсчетов ![]() . Первой процедурой
обработки, так же, как и в методе MAD, является
сортировка данных, в результате которой получается ранжированное по возрастанию
множество отсчетов
. Первой процедурой
обработки, так же, как и в методе MAD, является
сортировка данных, в результате которой получается ранжированное по возрастанию
множество отсчетов ![]() .
.
Последующие действия метода базируются на том, что
правостороннее засорение оказывает низкое влияние на отсчеты, значения которых
не превышают медианное. За счет этого для получения устойчивых оценок
формируется новая выборка ![]() путем нечетного
отображения:
путем нечетного
отображения:
|
|
|
где ![]() –
элемент из отсортированной выборки
–
элемент из отсортированной выборки ![]() , i – позиция данного элемента в ранжированном ряду.
, i – позиция данного элемента в ранжированном ряду.
В результате такой операции происходит отбрасывание отсчетов
из правой части выборки и на их позиции зеркально отображается относительно
медианы левая сторона ![]() .
.
Для получения конечного значения требуемых оценок параметров
математического ожидания ![]() и среднеквадратичного
отклонения
и среднеквадратичного
отклонения ![]() используются методы максимального
правдоподобия для нормального распределения, применяемые к сформированной
выборке
используются методы максимального
правдоподобия для нормального распределения, применяемые к сформированной
выборке ![]() :
:
|
(15) |
где ![]() –
элемент из множества
–
элемент из множества ![]() .
.
Основным достоинством данного метода являются малые вычислительные затраты, поскольку, в отличии от метода MAD, требуется всего лишь однократная сортировка данных. Также немаловажным достоинством является простота его аппаратной или программной реализации, так как данный метод состоит из линейной последовательности элементарных действий. Эти достоинства делают его пригодным для применения в составе автоматизированных систем обнаружения, производящих обработку поступающего сигнала в режиме реального времени.
Основным недостатком метода НОВ является принципиально
низкая эффективность получаемых точечных значений оценок параметров, которая
обуславливается неизбежной потерей информации о вероятностном распределении
данных из усеченной стороны отсортированного множества элементов ![]() , поскольку она не используются для
получения конечных значений оцениваемых параметров.
, поскольку она не используются для
получения конечных значений оцениваемых параметров.
Предлагаемый метод
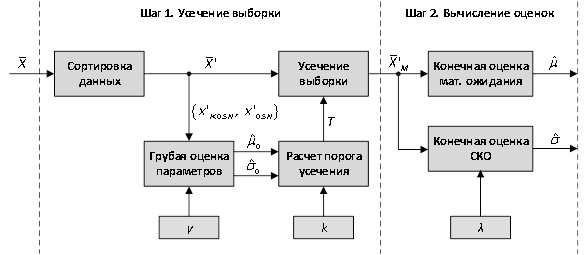
Предлагаемый метод вычисления оценок параметров сдвига и масштаба нормального распределения по набору реализаций случайной величины при наличии правостороннего засорения состоит из двух основных шагов. Целью первого шага является усечение выборки за счет отбраковки резко выделяющихся отсчетов на фоне остальных с помощью рассчитываемого порогового значения. Целью второго шага является получение конечных значений требуемых оценок по усеченной выборке, устойчивое к возможным ошибкам отбраковки на первом шаге. Общая последовательность действий в предлагаемом методе изображена на Рисунке 4.
Шаг усечения выборки. Первоочередным действием, так
же как и в ранее рассмотренных методах MAD и НОВ, является сортировка множества реализаций ![]() случайной величины объема N с целью получения
ранжированного по возрастанию ряда
случайной величины объема N с целью получения
ранжированного по возрастанию ряда ![]() :
:
|
|
|
и вся последующая обработка производится непосредственно над упорядоченными данными.
Основная идея усечения выборки заключается в том, что в
ранжированном множестве ![]() аномальные значения
будут занимать некоторое количество позиций с правой стороны, при этом начиная
с какого-то элемента
аномальные значения
будут занимать некоторое количество позиций с правой стороны, при этом начиная
с какого-то элемента ![]() данное множество не будет
содержать засорения. Однако поскольку количество элементов из
данное множество не будет
содержать засорения. Однако поскольку количество элементов из ![]() неизвестно и является случайной величиной
(3), то порог усечения
неизвестно и является случайной величиной
(3), то порог усечения ![]() можно рассчитать исходя из
левосторонней части выборки как
можно рассчитать исходя из
левосторонней части выборки как
|
(16) |
где ![]() –
полученная по левосторонней части
–
полученная по левосторонней части ![]() предварительная оценка
математического ожидания,
предварительная оценка
математического ожидания, ![]() – полученная по тем же
данным предварительная оценка среднеквадратичного отклонения,
– полученная по тем же
данным предварительная оценка среднеквадратичного отклонения, ![]() – некоторый заданный коэффициент
пропорциональности.
– некоторый заданный коэффициент
пропорциональности.
В качестве значения ![]() берется
медиана выборки (10), так же, как это и было сделано в методе MAD:
берется
медиана выборки (10), так же, как это и было сделано в методе MAD:
|
(17) |
Вычисление предварительного значения параметра
среднеквадратичного отклонения ![]() является более сложным.
Его значение может быть получено исходя из расстояния между медианой выборки и
некоторым отсчетом из её левой части:
является более сложным.
Его значение может быть получено исходя из расстояния между медианой выборки и
некоторым отсчетом из её левой части:
|
(18) |
где ![]() – один
из отсчетов левой части упорядоченной выборки
– один
из отсчетов левой части упорядоченной выборки ![]() , а
, а ![]() – коэффициент корректировки смещения, значение
которого зависит от позиции выбранного отсчета. При этом важным моментом,
оказывающим влияние на конечную эффективность предварительной оценки
– коэффициент корректировки смещения, значение
которого зависит от позиции выбранного отсчета. При этом важным моментом,
оказывающим влияние на конечную эффективность предварительной оценки ![]() и, в соответствии с (16), на точность
порога отсечения
и, в соответствии с (16), на точность
порога отсечения ![]() , является выбор позиции i отсчета
, является выбор позиции i отсчета ![]() .
.
При отсутствии выбросов в отсортированном множестве ![]() каждый элемент представляет собой
порядковую статистику, подчиняющуюся закону распределения:
каждый элемент представляет собой
порядковую статистику, подчиняющуюся закону распределения:
|
(19) |
где i
– положения порядковой статистики в вариационном ряду, ![]() –
плотность вероятности:
–
плотность вероятности:
|
|
|
а ![]() – функция
распределения:
– функция
распределения:
|
|
|
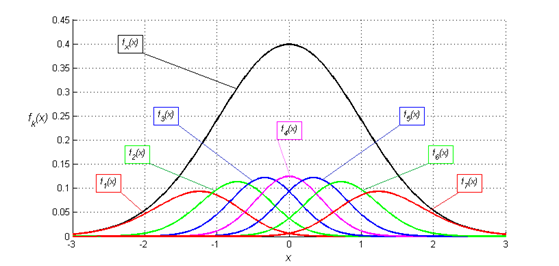
На Рисунке 5 представлены плотности распределения для порядковых статистик (19), сформированных из выборки объемом N = 7 элементов:
|
|
|
Рисунок 5. Распределение порядковых статистик для выборки из 7 элементов |
Из данного рисунка видно, что как математическое ожидание,
так и среднеквадратичное отклонение каждой порядковой статистики зависят от её
положения в вариационном ряду. Поэтому для достижения минимальной дисперсии
предварительной оценки ![]() необходимо выбирать такую
порядковую статистику из левосторонней части выборки
необходимо выбирать такую
порядковую статистику из левосторонней части выборки ![]() ,
среднеквадратичное отклонение которой будет минимально после нормирования
значения математического ожидания:
,
среднеквадратичное отклонение которой будет минимально после нормирования
значения математического ожидания:
|
|
|
где ![]() –
среднеквадратичное отклонение i-ой порядковой
статистики, а
–
среднеквадратичное отклонение i-ой порядковой
статистики, а ![]() функция распределения i-ой порядковой статистики после нормирования:
функция распределения i-ой порядковой статистики после нормирования:
|
(20) |
где ![]() –
математическое ожидание центральной порядковой статистики (медианы),
–
математическое ожидание центральной порядковой статистики (медианы), ![]() – математическое ожидание i-ой порядковой статистики.
– математическое ожидание i-ой порядковой статистики.
В качестве примера на Рисунке 6 представлены значения среднеквадратичного отклонения порядковых статистик от 1 до 9 при объеме выборке N = 25 после процедуры нормирования (20).
|
|
|
Рисунок 6. Среднеквадратичное отклонение нормированных порядковых статистик |
Из представленного рисунка видно, что наименьшим
среднеквадратичным отклонением при объеме выборки 25 элементов обладает
порядковая статистика, занимающая 2 позицию в ранжированном по возрастанию
ряду. Следовательно, её использование для получения предварительной оценки ![]() (18) наиболее предпочтительно.
(18) наиболее предпочтительно.
В Таблице 1 представлены индексы
i наилучших позиций порядковых статистик для (18)
и значения корректировки смещения ![]() при различных
значениях объема выборки N.
при различных
значениях объема выборки N.
|
Таблица 1. Позиции порядковых статистик и коэффициент корректировки |
|||||
|
Объем, N |
Индекс, i |
Корректировка, |
Объем, N |
Индекс, i |
Корректировка, |
|
3 |
1 |
0.85 |
63 |
7 |
1.58 |
|
15 |
2 |
1.74 |
75 |
9 |
1.54 |
|
27 |
4 |
1.56 |
87 |
11 |
1.52 |
|
39 |
5 |
1.51 |
99 |
12 |
1.59 |
|
51 |
6 |
1.64 |
111 |
14 |
1.56 |
Значение коэффициента
пропорциональности k для формирования конечного
значения порога отсечения T в
(16) выбирается исходя из вероятности ложного срабатывания, то есть принятия
решения о выбросе по отношению к элементу из нормального распределения.
Поскольку пороговое значение T рассчитывается по
полученным предварительным оценкам ![]() и
и ![]() , то оно обладает некоторым вероятностным
распределением. На Рисунке 7 представлены законы распределения вероятности для
исходной выборки
, то оно обладает некоторым вероятностным
распределением. На Рисунке 7 представлены законы распределения вероятности для
исходной выборки ![]() без выбросов и пример закона
распределения порогового значения T
при различных значениях коэффициента k.
без выбросов и пример закона
распределения порогового значения T
при различных значениях коэффициента k.
|
|
|
Рисунок 7. Распределение порога T при различных значениях коэффициента k
|
Из представленного рисунка видно, что слишком малые значения k (k = 3) могут приводить к ошибочной отбраковке, а при слишком больших значениях данного коэффициента (k = 8) велика вероятность пропуска засорения.
В соответствии с этим оптимальное значение k можно установить таким образом, чтобы «три сигмы»
исходной выборки ![]() пересекались с «тремя сигмами»
распределения порогового значения T:
пересекались с «тремя сигмами»
распределения порогового значения T:
|
|
|
где ![]() и
и ![]() - моменты распределения формируемого
порога T. На представленном рисунке данное
значение соответствует k = 5.
- моменты распределения формируемого
порога T. На представленном рисунке данное
значение соответствует k = 5.
В результате из отсортированного множества ![]() и рассчитанного порогового значения T формируется новая выборка
и рассчитанного порогового значения T формируется новая выборка ![]() усеченных
данных:
усеченных
данных:
|
|
|
объем M
которой меньше или равен объему исходной выборки ![]() .
.
Шаг вычисления оценок. Для получения оценки
математического ожидания ![]() используется метод
максимального правдоподобия:
используется метод
максимального правдоподобия:
|
(21) |
Для оценки среднеквадратичного отклонения ![]() также можно использовать метод
максимального правдоподобия, как это было сделано в методе НОВ (15), однако
поскольку
также можно использовать метод
максимального правдоподобия, как это было сделано в методе НОВ (15), однако
поскольку ![]() представляет собой ранжированный ряд, то
более удобно использовать линейную комбинацию его элементов:
представляет собой ранжированный ряд, то
более удобно использовать линейную комбинацию его элементов:
|
(22) |
где ![]() –
коэффициент корректировки смещения,
–
коэффициент корректировки смещения, ![]() – весовые
коэффициенты.
– весовые
коэффициенты.
При этом значения весовых коэффициентов ![]() для левой части выборки принимаются –1, а
для правой части +1:
для левой части выборки принимаются –1, а
для правой части +1:
|
|
|
Выбор именно таких значений преследует сразу две цели. Во-первых, таким образом достигается сокращение вычислений. Во-вторых, данные коэффициенты минимизируют влияние ошибки пропуска выбросов, которые возможны на первом шаге. Недостатком такого выбора является снижение эффективности значения оценки параметра сдвига за счет отличия от оптимально рассчитанных для нормального распределения значений [23].
Состоятельность и несмещенность оценок
Оценки параметров сдвига и масштаба ![]() и
и
![]() нормального распределения, получаемые в
соответствии с предлагаемым методом, должны обладать свойствами состоятельности
и несмещенности.
нормального распределения, получаемые в
соответствии с предлагаемым методом, должны обладать свойствами состоятельности
и несмещенности.
Для исследования свойства состоятельности проводился эксперимент численного моделирования по методу Монте-Карло [24], в ходе которого генерировалось 1000 выборок объема от 15 до 200 с шагом увеличения в 2 элемента, подчиняющихся стандартному нормальному распределению:
|
(23) |
Для каждого объема выборки производилось измерение параметров сдвига и масштаба предлагаемым методом и в соответствии с (4) оценивалась вероятность отклонения полученных оценок от истинных значений.
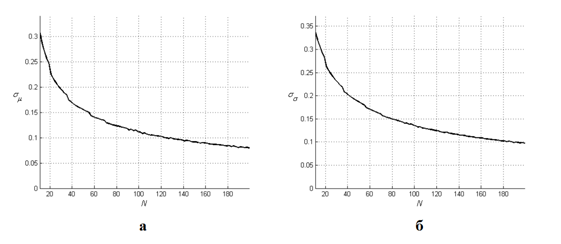
На Рисунке 8 представлены результаты данного эксперимента: на (а) изображен график зависимости отклонения оценки математического ожидания от объема выборки, а на (б) такая же зависимость для оценки среднеквадратичного отклонения.
|
|
|
Рисунок 8. Зависимость отклонения оценок от объема выборки |
Из представленных графиков видно, что с увеличением объема выборки N разброс каждой из оценок уменьшается, что доказывает их состоятельность.
Свойство несмещенности (5) для оценки математического ожидания
![]() выполняется в силу использования для
расчета конечного значения метода максимального правдоподобия (21). Смещение
оценки среднеквадратичного отклонения
выполняется в силу использования для
расчета конечного значения метода максимального правдоподобия (21). Смещение
оценки среднеквадратичного отклонения ![]() предлагаемым
методом корректируется с помощью коэффициента
предлагаемым
методом корректируется с помощью коэффициента ![]() ,
используемого в (22).
,
используемого в (22).
Сравнительный анализ методов
Вычислительные затраты. В Таблице 2 представлена зависимость количества требуемых элементарных операций методами MAD, НОВ и предлагаемым методом (ПМ) от объема выборки для получения конечного значения оценок математического ожидания и среднеквадратичного отклонения.
|
Таблица 2. Количество операций для различных методов оценки |
|||
|
Метод Операция |
MAD |
НОВ |
ПМ |
|
Сумма |
N |
2.5·N |
2·N+1 |
|
Произведение |
2 |
N |
2 |
|
Деление |
0 |
2 |
1 |
|
Сравнение |
2·N·log2(N) |
N·log2(N) |
N·(log2(N) + 1) |
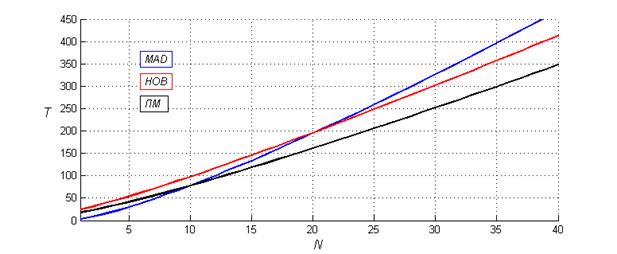
Для количественного сравнения требуемых операций при реализации на цифровом вычислительном устройстве сделано предположение о том, что операции суммирования и сравнения занимают 1 такт, операция произведения – 2 такта, а операция деления – 10 тактов. Зависимость совокупной сложности вычислений при таком предположении от объема выборки представлена на Рисунке 9.
|
|
|
Рисунок 9. Зависимость отклонения оценок предлагаемым методом от объема выборки |
Из представленного графика видно, что все рассматриваемые методы обладают схожей вычислительной сложностью. Однако при объемах выборки N, до 10 элементов, наименьшее количество вычислений требует метод MAD, но при увеличении объема N наименьшее количество вычислений занимает предлагаемый метод.
Эффективность оценок. Для получения значения эффективности оценок исследуемых методов при отсутствии выбросов проводился следующий эксперимент. С помощью численного моделирования формировались выборки объемом N от 7 до 200 с шагом увеличения в 2 элемента, каждая из которых подчиняется стандартному нормальному закону распределения (23). Для каждого задаваемого объема N производилась генерация 1000 различных выборок. По полученным данным с помощью методов MAD, НОВ и ПМ формировались оценки математического ожидания и среднеквадратичного отклонения.
На Рисунке 10 представлен пример полученных оценок по сформированному набору данных с объемом N = 63 элемента: на (а) представлены оценки метода MAD, на (б) оценки метода НОВ, а на (в) полученные оценки с помощью ПМ.
|
|
|
Рисунок 10. Полученные оценки разными методами для объема выборки N = 63 |
По оси абсцисс отложены значения математического ожидания, по оси ординат отложены значения среднеквадратичного отклонения. Каждая точка на рисунках обозначает пару оценок, полученных по одному из наборов входных данных. Истинные значения параметров распределения обозначены точкой малинового цвета. Для сравнения овалом красного цвета обозначена область разброса эффективных оценок, полученных методом максимального правдоподобия.
Из представленного рисунка видно, что ПМ обладает наибольшей кучностью выдаваемых значений по отношению к методам MAD и НОВ, что свидетельствует об его большей эффективности. При этом наибольшим разбросом оценок обладает метод MAD, что говорит об его наименьшей эффективности. Для метода НОВ визуально заметна протяженность области разброса оценок вдоль прямой, проходящей под углом 45°. Такое явление свидетельствует о корреляции получаемых данным методом оценок.
В Таблице 3 представлены результаты измерения значения эффективности оценок каждого метода, полученные по выражению (6).
|
Таблица 3. Значения эффективность рассматриваемых методов |
|||
|
Метод |
MAD |
НОВ |
ПМ |
|
Эффективность, % |
24 |
32 |
82 |
Из представленной таблицы видно, что для ПМ асимптотическая эффективность на стандартном нормальном распределении составляет 82% и он обладает в 3.4 раза большей эффективностью по отношению к методу MAD, и в 2.5 раза большей эффективностью по отношению к методу НОВ.
Устойчивость к засорению. Для исследования
устойчивости результатов различных методов к возможным возникновениям
правосторонних выбросов генерировалось 1000 выборок с фиксированным объемом N = 101, подчиняющихся стандартному нормальному закону
распределения (23), которые затем засорялись по модели (8) с различными
значениями параметра ![]() .
.
В качестве распределения выбросов ![]() использовался
равномерный закон распределения на участке от 0 до 20:
использовался
равномерный закон распределения на участке от 0 до 20:
|
|
|
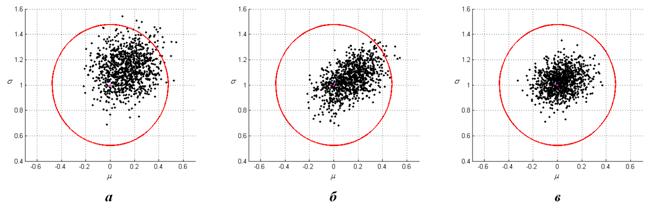
На Рисунке 11 для примера представлены оценки параметров
математического ожидания и среднеквадратичного отклонения, полученные методами MAD (а), НОВ (б) и ПМ (в) по
зашумленной выборке с параметром засорения ![]() .
.
|
|
|
Рисунок 11. Полученные оценки для объема выборки N = 63 при засорении выборки ε = 10% |
На каждом из представленных рисунков точкой малинового цвета отмечено истинное значение параметров нормального распределения, а красным овалом область разброса оценок зашумленной выборки методами максимального правдоподобия без учета их смещения.
Из представленных рисунков видно, что оценки, получаемые методом MAD, значительно отклоняются в большую сторону по отношению к истинным значениям параметров. Для метода НОВ наибольшее отклонение наблюдается у оценки математического ожидания. При этом оценки параметров, полученные с помощью ПМ, имеют наименьшее смещение относительно истинных значений, что свидетельствует об их наибольшей устойчивости к наличию выбросов при заданном параметре засорения.
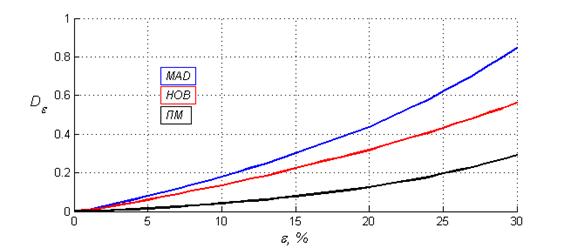
На Рисунке 12 представлен график зависимости отклонения
оценок параметров (7), получаемых исследуемыми методами, от процента засорения
выборки ![]() .
.
|
|
|
Рисунок 12. Зависимость отклонения
оценок от процента засорения выборки |
Из представленного графика видно, что для принимаемой модели
засорения со значениями ![]() от 0% до 30%
полученные с помощью ПМ оценки имеют наименьше отклонение от истинных значений
по отношению к оценкам, полученным с помощью методов MAD и НОВ. ПМ обеспечивает приблизительно в 3 раза меньшее
отклонение по отношению методу MAD, и в 2.1 раза
меньшее отклонение по отношению к методу НОВ.
от 0% до 30%
полученные с помощью ПМ оценки имеют наименьше отклонение от истинных значений
по отношению к оценкам, полученным с помощью методов MAD и НОВ. ПМ обеспечивает приблизительно в 3 раза меньшее
отклонение по отношению методу MAD, и в 2.1 раза
меньшее отклонение по отношению к методу НОВ.
Заключение
Задача устойчивой оценки параметров распределения шумовой составляющей поступающего на обработку цифрового сигнала является неотъемлемой частью общей задачи обнаружения некогерентной последовательности однополярных импульсов на фоне аддитивного гауссовского шума с неизвестными параметрами функции распределения. Её сложность заключается во влиянии амплитуд импульсов на получаемые оценки параметров сдвига и масштаба, которое в конченом итоге приводит как к пропуску сигнала, так и к неверному измерению амплитуд при использовании стандартных методов.
Данная задача схожа с классической для робастной статистики задачей, в которой шумовая составляющая принимается за набор реализаций случайной величины, подчиняющейся нормальному закону распределения, а импульсный сигнал рассматривается в качестве засорения, функция распределения которого неизвестна. Отличие заключается в том, что в рамках поставленной задачи импульсный сигнал является однополярным, следовательно, засорению подвергается только левый или правый хвост гистограммы отсчетов.
В данной статье рассмотрены несколько из существующих методов устойчивой оценки, применение которых возможно в составе цифровых вычислительных устройств обнаружения импульсного сигнала в режиме реального времени. Однако для данных методов характерна низкая эффективность получаемых значений.
Предложен метод двухшаговой оценки параметров сдвига и масштаба нормального распределения, базирующийся на закономерностях порядковых статистик. Предложенный метод не содержит итерационных процедур, не требует больших вычислительных затрат и пригоден для автоматизированной обработки данных в режиме реального времени.
Оценки параметров, получаемые с помощью предлагаемого метода, являются состоятельными и несмещенным, что было исследовано с помощью численного моделирования. Вычислительная сложность данного метода схожа с вычислительной сложностью ранее рассмотренных методов MAD и НОВ.
Асимптотическая эффективность получаемых с помощью предлагаемого метода оценок на стандартном нормальном распределении без засорения составляет 82%, что в 3.4 раза больше эффективности метода MAD (24%) и в 2.5 раза больше эффективности метода НОВ (32%).
Исследование с помощью численного моделирования устойчивости методов к правостороннему засорению выборки показали, что оценки, полученные с помощью предлагаемого метода, отклоняются от истинных значений в 3 раза меньше, чем оценки метода MAD и в 2.1 раза меньше, чем оценки, полученные с помощью метода НОВ.
Литература