УДК 004.312

ФУНКЦИОНАЛЬНОЕ МОДЕЛИРОВАНИЕ И СИНТЕЗ АППАРАТНЫХ КРИПТОГРАФИЧЕСКИХ СРЕДСТВ ЗАЩИТЫ ИНФОРМАЦИИ НА ЛИНЕЙНЫХ РЕКУРРЕНТНЫХ РЕГИСТРАХ СДВИГА

 

А. Б. Сизоненко ¹, В. В. Меньших ²

¹ Краснодарский университет МВД России

² Воронежский институт МВД России

 

Статья получена 9 апреля 2015 г.

 

Аннотация. Представлен способ технической реализации линейного рекуррентного регистра сдвига (ЛРРС), вырабатывающего за один такт несколько элементов псевдослучайной последовательности. Приведены и обоснованы показатели и критерии эффективности технической реализации ЛРРС. По выбранным показателям и критериям оценена эффективность модифицированной схемы на конкретном примере. Приведен алгоритм моделирования и синтеза высокопроизводительных аппаратных средств криптографической защиты информации по критерию максимальной производительности при имеющихся ограничениях по сложности. Для моделирования высокопроизводительной технической реализации шифраторов, имеющих в своем составе более одного ЛРРС, предложено использовать математический аппарат сетей Петри.

Ключевые слова: моделирование средств защиты информации; линейный рекуррентный регистр сдвига; параллельные вычисления; криптографические преобразования; поточные шифры.

Abstract. Method of technical realization of a Linear Feedback Shift Register (LFSR), generating multiple elements of pseudo-random sequence in one cycle is presented. Indicators and criteria of performance of technical implementation LFSR are given and justified. The effectiveness of the modified circuit is assessed using selected indicators and criteria of performance for specific example. Algorithm simulation and synthesis of high-performance hardware cryptographic protection of information on the criterion of maximum productivity with existing limits on complexity is reduced. The mathematical apparatus of Petri nets is proposed to use for modeling high-performance technical implementation encoders, having in its composition more than one LFSR.

Keywords: modeling of information security; Linear Feedback Shift Register; parallel computing; cryptographic transformations; stream cipher.

Введение

Линейные рекуррентные регистры сдвига, несмотря на то, что вырабатывают псевдослучайную последовательность (ПСП) с невысокой линейной сложностью, находят широкое применение при построении поточных шифраторов [7]. Это обусловлено простотой их реализации с помощью цифровой аппаратуры и возможностью усложнения вырабатываемой ими ПСП. Аппаратная реализация, включающая регистр сдвига и сумматоры по модулю два, вырабатывает один бит последовательности за один такт. В статье рассматривается методика синтеза высокопроизводительных средств криптографической защиты информации на основе линейных рекуррентных регистров сдвига. При этом не затрагиваются вопросы разработки новых криптоалгоритмов, а приводятся разработанные алгоритмы синтеза более производительных устройств, реализующих известный шифр на основе ЛРРС. Повышение производительности достигается переопределением функции обратной связи ЛРРС, что позволяет за один такт функционирования получить несколько элементов последовательности. Функция обратной связи определяется с помощью формализованного алгоритма получения коэффициентов системы линейных рекуррентных уравнений.

Для получения технической реализации с требуемыми характеристиками необходимо прибегнуть к методам математического моделирования. В данном случае будут использованы детерминированные модели цифровых устройств. Показателем сложности цифровых устройств является так называемая «цена по Квайну», определяемая как суммарное количество входов логических элементов, образующих цифровое устройство. В связи с этим, с помощью моделирования возможно решение двух задач:

определение структуры криптографического средства защиты информации, имеющего максимальную производительность при ограничении стоимости (по Квайну);

обеспечение требуемой производительности при отсутствии ограничений по стоимости.

Для решения первой задачи в силу небольшого количества элементов, может быть предложен итерационный алгоритм простого перебора, при решении второй задачи для моделирования процесса функционирования сложных криптоалгоритмов может быть использован математический аппарат сетей Петри.

Результатом моделирования являются количественные показатели эффективности схемы шифратора – стоимость и  быстродействие. Моделирование позволяет получить исходные данные для синтеза схемы шифратора с требуемыми параметрами. Реализуемая криптоалгоритмом функция остается неизменной, меняются лишь значения показателей эффективности. С функциональной точки зрения получаются идентичные устройства. При моделировании не учитываются показатели надежности (при увеличении количества элементов), времени переключения логических элементов, помехозащищенности и т.д. Верификациям моделей осуществлена путем разработки схемотехнических решений для ряда криптоалгоритмов и изложена в публикациях [2, 3, 4, 5].

1. Понятие линейного рекуррентного регистра сдвига и синтез устройств, позволяющих за один такт вычислять несколько элементов псевдослучайной последовательности

ЛРРС с обратными связями состоит из регистра сдвига и схемы, реализующей функцию обратной связи, построенную на основе неприводимого образующего полинома степени  [7, 8]:

,

где  – коэффициенты связей.

На основе образующего полинома строится линейное рекуррентное уравнение. При выполнении вычислений в GF(2) оно имеет вид [6, 8]:

,                                                                     (1)

где коэффициент t+1 обозначает последующее состояние;  – сумма по модулю два.

В [1, 2] представлены способы технической реализации ЛРРС, позволяющие за один такт получить несколько элементов псевдослучайной последовательности. Для этого необходимо произвести декомпозицию булевых функций, описывающих функционирование ЛРРС, таким образом, чтобы за один такт функционирования получить несколько значений последовательности. Исходными данными для построения такой схемы будут: длина ЛРРС – n; начальное состояние ЛРРС – ; линейное рекуррентное уравнение , построенное по образующему полиному; количество моделируемых шагов работы –  [1, 2]. Необходимо найти такую систему булевых функций F(X), задающую обратные связи при приведении ЛРРС к виду (рис. 1.), позволяющему за один такт получить элементов псевдослучайной последовательности.

 

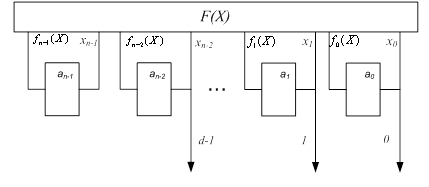
Рис. 1 Функциональная схема ЛРРС
с переопределенной функцией обратной связи

 

Линейную рекуррентную последовательность над полем (в данном случае GF(2)), определяемую линейным рекуррентным уравнением (1), можно связать с матрицей [8]:

 

Так как последующее состояние ЛРРС можно найти, умножив матрицу A на вектор предыдущего заполнения : , то состояние через d шагов функционирования можно определить выполнив преобразование  [8].

Матрица  однозначно задает систему функций обратных связей :

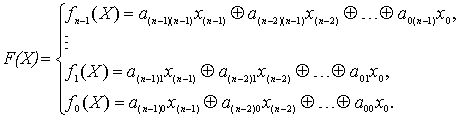
Для того чтобы строить рекуррентные регистры сдвига, позволяющие получать за один такт функционирования количество элементов последовательности больше чем n, то схема должна быть дополнена справа недостающим количеством регистров для хранения вычисленных элементов последовательности. В этом случае (d>n) необходимо сохранить в одной матрице промежуточные результаты возведения матрицы A в степень D. Назовем такую матрицу расширенной матрицей коэффициентов и обозначим . Алгоритм формирования такой матрицы подробно описан в [11] и заключается в следующем:

Алгоритм 1.

Шаг 1. Получить квадратную матрицу  из матрицы  путем выделения из нее первых n строк матрицы . Для первой итерации .

Шаг 2. Умножить вектор коэффициентов линейного рекуррентного уравнения на матрицу :

,                                                                                                 (2)

Шаг 3. Подставить полученный вектор в первую строку матрицы, а остальные строки сдвинуть на одну вниз. В результате получим матрицу коэффициентов .

Для получения матрицы коэффициентов  системы выражений, описывающих d элементов последовательности, необходимо шаги 1-3 алгоритма 1 выполнить d раз.

Если то последние n строк матрицы , содержащей начальную единичную матрицу, необходимо отбросить. Если же d<n, то отбрасывается последние d строк, чтобы осталась квадратная матрица .

Шаги 2 и 3 эквивалентны возведению матрицы A в степень, однако позволяет сократить количество операций, исключив операцию умножения матриц. Это возможно благодаря тому, что матрица A в первой строке содержит вектор H, а далее содержит единичную матрицу. Наличие в матрице A единичной матрицы дает сдвиг вниз предыдущих значений при возведении в степень. В данном алгоритме просто добавляется новая строка к матрице, полученной на предыдущем шаге функционирования.

В [11] расширенная матрица коэффициентов использовалась для повышения производительности программной реализации поточных шифраторов на основе ЛРРС. Ниже рассмотрим пример, позволяющий использовать ее для формализации процесса построения технических устройств, позволяющих за один такт вырабатывать несколько элементов псевдослучайной последовательности, соответствующих заданному линейному рекуррентному уравнению.

Пример 1. Для образующего полинома  образующая матрица для построения схемы, вырабатывающей 6 элементов псевдослучайной последовательности за один такт будет выглядеть следующим образом:

Схема, построенная по этой матрице, приведена на рис. 2.

 

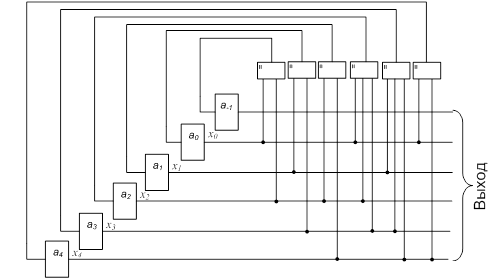
Рис. 2. Пример реализации схемы ЛРРС

 

2. Показатели и критерии эффективности технической реализации криптографических средств защиты информации. Постановка задачи на моделирование

Введем обозначения:

 – стоимость исходной схемы.

 – стоимость модифицированной схемы, выполняющей эквивалентную функцию.

 – производительность исходной схемы, определяемая как отношения количества вырабатываемых элементов последовательности за единицу времени: .

 – производительность модифицированной схемы, при неизменной тактовой частоте.

Введем показатель эффективности технической реализации:

Будем считать, что модифицированная схема будет эффективна, когда:

,                                                                                                           (3)

или

                                                                                                (4)

где ,  – показатели эффективности исходной и модифицированной схем соответственно.

Практика показывает, что наименьшее число конструктивных элементов (корпусов интегральных микросхем), а, следовательно, и минимальную стоимость, имеют цифровые схемы с минимальной ценой по Квайну [10, 9].

Сложность (цена) по Квайну определяется суммарным числом входов логических элементов в составе схемы [10, 9]. При такой оценке единица сложности – один вход логического элемента. Цена инверсного входа равна двум.

Такой подход к оценке сложности обусловлен тем, что сложность схемы определяется булевой функцией (набором булевых функций), на основе которых строится схема. Для нормальных форм сложность по Квайну будет определяться суммарным количеством переменных, инверсий переменных и термов, количеством термов.

Соотношение (3) показывает, что эффективным техническим средством защиты информации, реализующим логические вычисления, будет то средство, в котором за счет незначительного усложнения схемы, а, следовательно, и незначительного увеличения стоимости, удастся непропорционально больше повысить производительность.

Критерием эффективности будет максимальное значение показателя эффективности : .

Пример 2. Рассчитаем показатели эффективности для схемы примера 1. Так как D-триггер, входящий в состав ЛРРС, строится на четырех двухвходовых логических элементах И-НЕ, то цена по Квайну одного такого элемента будет равна 8. Следовательно, , а . Таким образом, данная реализация будет эффективной, так как выполняется соотношения (3), (4).

Построим графики, отображающие зависимость коэффициента эффективности К_Э и соотношение стоимости модифицированной схемы и исходной () от количества бит псевдослучайной последовательности, вырабатываемых модифицированной схемой за один такт  (рис. 3).

 

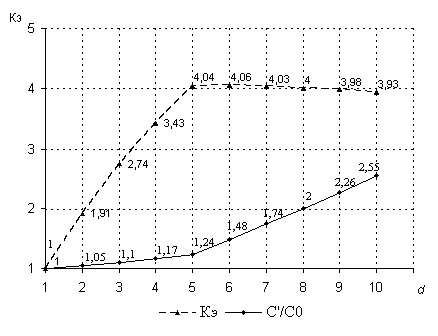
Рис. 3. Зависимости стоимости и эффективности модифицированной схемы

Более резкий рост стоимости начиная с d=6, т.е. количества вырабатываемых бит за один такт, превышающим степень образующего полинома и, следовательно, длину ЛРРС, объясняется необходимостью добавления в схему по одному D-триггеру при увеличении d на единицу (при d>n).

Из графиков видно, что для данного рекуррентного уравнения коэффициент эффективности К_Э будет превышать 1 для схем, вырабатывающих за один такт 2 и более бит. Возникает вопрос – какая же из реализаций будет наиболее эффективной? Ответ на этот вопрос будет зависеть от многих факторов, в том числе от имеющихся у разработчика ресурсов и необходимой максимальной производительности.

Подобрать оптимальную структуру, исключив трудоемкий процесс сборки и тестирования каждой схемы, можно с помощью методов математического моделирования. Объектом моделирования будет выступать функциональная сторона разрабатываемого устройства, а если быть более точным – эффективность схемотехнической реализации функциональной стороны с точки зрения производительность/стоимость. Таки образом, целями моделирования должно стать определение оптимальной структуры разрабатываемого устройства при следующих условиях:

определение структуры криптографического средства защиты информации, имеющего максимальную производительность при ограничении стоимости (по Квайну) : , при .

обеспечение требуемой производительности П при отсутствии ограничений по стоимости: .

3. Алгоритм моделирования и синтеза высокопроизводительных аппаратных средств криптографической защиты информации

Алгоритм функционального моделирования аппаратных средств криптографической защиты информации на основе ЛРРС при условии достижения максимальной производительности при имеющихся ограничениях на стоимость (C_max), представлен на рис. 4.

 

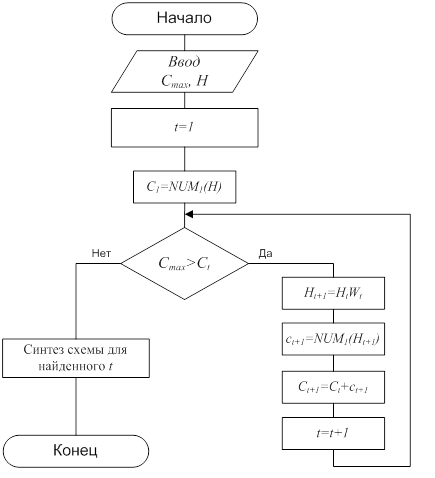
Рис. 4. Алгоритм функционального моделирования средств защиты информации с заданной
предельной стоимостью и максимальной производительностью

Алгоритм заключается в моделировании сложности (стоимости) схемы при последовательном увеличении количества бит последовательности, одновременно вырабатываемых за один такт. При превышении стоимости моделируемой схемы относительно заданного предельного значения стоимости, работа алгоритма останавливается и осуществляется синтез схемы в соответствии с матрицей коэффициентов, полученной по алгоритму 1.

До этого нами рассматривалась оценка эффективности простейших устройств, содержащих один ЛРРС. Реальные шифраторы значительно сложнее и могут содержать несколько ЛРРС. Для оценки производительности таких схем можно использовать математический аппарат временных сетей Петри, с помощью которых можно моделировать скорость выработки элементов псевдослучайной последовательности.

Для примера рассмотрим генератор скалярного произведения, описанный в [7]. В генераторе скалярного произведения (рис. 5) используется два ЛРРС с разными тактовыми частотами и, возможно, разной длины. ЛРРС 1 имеет длину n⁽¹⁾ и показатель скорости d⁽¹⁾, ЛРРС 2 соответственно – n⁽²⁾ и d⁽²⁾. Ключом является начальное состояние ЛРРС – X₀⁽¹⁾ и X₀⁽²⁾. Отдельные биты этих ЛРРС объединены операцией логического умножения (AND), а затем, для получения выходного бита они объединяются посредством сумматора по модулю два, т. е. вычисление каждого i-ого бита гаммы осуществляется по алгоритму:

1. Сдвинуть ЛРРС 1 на d⁽¹⁾ шагов.

2. Сдвинуть ЛРРС 2 на d⁽²⁾ шага.

3. Вычислить знак гаммы: y_i= = x_k⁽¹⁾& x_k⁽²⁾.

 

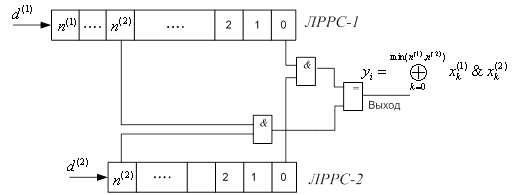
Рис. 5.   Генератор скалярного произведения

Для поиска оптимальной структуры шифратора в соответствии с заданными критериями, применим методы имитационного моделирования. На рис. 6 показана сеть Петри, с помощью которой можно оценить производительность генератора скалярного произведения.

 

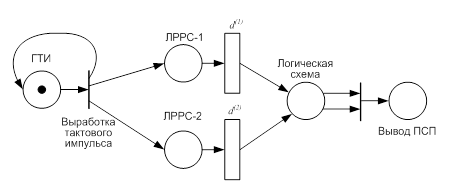
Рис. 6.

На рис. 6 d⁽¹⁾ и d⁽²⁾ обозначает длительность непримитивного события , ГТИ – генератор тактовых импульсов. Количество шагов функционирования для выработки одного элемента ПСП будет соответствовать количеству тактов ГТИ. Меняя d⁽¹⁾ и d⁽²⁾ добиваемся требуемой производительности либо максимальной производительности при ограничениях на стоимость. В связи с небольшим количеством состояний, соответствующих количеству ЛРРС, и переходов, размерность задачи мала, что позволяет для определения оптимальной структуры шифратора использовать метод простого перебора. Оценка стоимости для каждого ЛРРС, входящего в схему шифратора, производится по алгоритму (рис.  4).

Стоимость всей схемы вычисляется по формуле:

,

где k – количество ЛРРС в шифраторе.

Заключение

В статье адаптирован метод вычисления значений псевдослучайной последовательности путем перемножения матриц для получения технической реализации поточных шифраторов, построенных на основе ЛРРС. Такой способ применим в случаях, когда необходимо повысить скорость функционирования шифратора, при имеющихся ограничениях по стоимости схемы.

Направлением дальнейшего исследования является разработка комплекса программ, реализующего представленные методы моделирования эффективности  технической реализации поточных шифраторов на основе ЛРРС.

 

Литература 

1.  Сизоненко А.Б. Параллельная схемотехническая реализация линейного рекуррентного регистра сдвига // Проектирование и технология электронных средств. 2012. № 2. С. 43-47.

2.  Сизоненко А.Б. Логико-математическое моделирование и синтез алгоритмов функционирования средств и систем защиты информации. – Краснодар: Краснодарский университет МВД России, 2013. – 146 с.

3.  Сизоненко А.Б. Многоканальный цифровой источник шума на основе рекуррентного регистра сдвига // Спецтехника и связь – 2012 – № 3 – С. 51–54.

4.  Сизоненко А.Б. Высокопроизводительная схемотехническая реализация криптографического многоскоростного генератора скалярного произведения // Инженерный вестник Дона – 2012 – № 3 (Электронный журнал http://www.ivdon.ru/magazine/archive/n3y2012/page/4).

5.  Сизоненко А.Б. Высокопроизводительная схемотехническая реализация генераторов гаммы с неравномерным движением / Проектирование и технология электронных средств. – № 1 – 2012. – С 50-54.

6.  Фомичев В. М. Дискретная математика и криптология: Курс лекций / Под общ ред. Н. Д. Подуфалова. М.: Диалог-МИФИ, 2003. 400 с.

7.  Шнайер Б. Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си. М.: Издательство ТРИУМФ, 2003. 816 с.

8.  Лидл Р., Нидеррайтер Г. Конечные поля. Т. 1,2. — М.: Мир, 1998.

9.  Угрюмов Е.П. Цифровая схемотехника: учеб. пособие для вузов. – 3-е изд., перераб. и доп. – СПб.: БХВ-Петербург, 2010. – 816 с.

10. Рощин А.Г., Половов Р.М. Теория автоматов. Часть I. Учебное пособие – М.: МГТУ ГА, 2007. – 96 с.

11. Sizonenko A.B., Men’shikh V.V. Software Implementation of Parallel Matrix Computations for Linear Recurrent Sequence and Numerical Methods for Estimating its Efficiency // Automatic Control and Computer Sciences, 2015, Vol. 49, No. 2, pp. 76–81.

12.  Чернышев А.Ю. Электронная и микропроцессорная техника: учебное пособие / А.Ю. Чернышев, Е.А. Шутов. - Томск: Изд-во Томского политехнического университета, 2010. - 135 с.