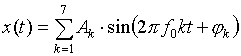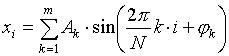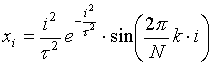| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 7, 2001 |  |
ВЛИЯНИЕ ФОРМЫ ЗОНДИРУЮЩЕГО СИГНАЛА НА ТОЧНОСТЬ РАДИОЛОКАЦИИ СЛОИСТЫХ СРЕД
А. Г. Оганесян, И. Б. Чайковский
Государственный университет "Львовская политехника"
Получена 18 апреля 2001 г.
В статье приведены погрешности измерения толщины морских льдов в зависимости от формы радиолокационных сигналов, спектрального состава и некоторых методов их цифровой обработки.
Проникающей (подповерхностной) радиолокацией занимаются достаточно давно (приоритет принадлежит лаборатории профессора М.И.Финкельштейна Рижского института инженеров Гражданской авиации – РИИГА, в которой ещё 25 лет назад был создан первый самолётный измеритель толщины льда). Тем не менее, до сих пор многое остаётся не ясным. Особенно при зондировании слоистых дисперсных сред, примером которых является дрейфующий соленый морской лёд. Он радиопрозрачен в довольно узком диапазоне радиочастот: примерно от 25 до 200 МГц. На частотах ниже 25 МГц диэлектрическая проницаемость льда резко возрастает и сильно зависит от температуры и возраста льда. На частотах более 200 МГц экспоненциально возрастает затухание [1]. Поэтому использование сверхширокополосных зондирующих сигналов в значительной мере лишена смысла, поскольку ширина их спектра ограничивается окном прозрачности отражающего слоя. И если при сверхширокополосном сигнале можно пренебречь его формой и длительностью (обычно она находится в пределах допустимой разрешающей способности), то формой сигналов с ограниченным спектром пренебречь нельзя – во многих случаях точность измерений зависит именно от формы зондирующего сигнала.
Первый (и последний) промышленный вариант радиолокационного измерителя толщины льдов, идея которого предложена и разработана в Рижском институте инженеров Гражданской авиации [2], получил название "Аквамарин" и использовался для разведки ледовой обстановки Северного Ледовитого океана. Отражённый сигнал "Аквамарина" представлял собой сумму семи синусоид
амплитуды Ak
и фазы
![]() которых устанавливал оператор.
Нижняя частота в спектре f0 = 25 МГц. Во время полёта над
спокойной морской поверхностью оператор, вращая ручки регулировки амплитуд и
фаз, старался получить импульсный сигнал с максимальной скважностью при периоде
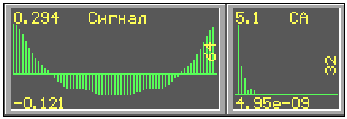
повторения 1/f0. На рис. 1 показан такой сигнал и его спектр
амплитуд.
которых устанавливал оператор.
Нижняя частота в спектре f0 = 25 МГц. Во время полёта над
спокойной морской поверхностью оператор, вращая ручки регулировки амплитуд и
фаз, старался получить импульсный сигнал с максимальной скважностью при периоде
повторения 1/f0. На рис. 1 показан такой сигнал и его спектр
амплитуд.
Рис.1. Сигнал "Аквамарина"
"Аквамарин"
работал по принципу обычного импульсного радиовысотомера с индикатором типа А.
Разница только в том, что импульсный радиовысотомер в пределах периода
повторения работает без неоднозначности, а импульсный измеритель толщины льда
имеет неоднозначность, равную половине периода повторения. Это вызвано тем, что
отношение амплитуд сигналов, отражённых верхней и нижней поверхностями льда,
может быть и больше и меньше единицы. Поэтому невозможно отличить, какой из
импульсов отразился от верхней поверхности, а какой от нижней. Для "Аквамарина"
период повторения импульсов равен T=1/f0=40 нс. Полагая, что
средняя относительная диэлектрическая проницаемость льда
![]() =3,2, нетрудно получить
максимальное значение толщины льда, которое можно измерить без неоднозначности:
=3,2, нетрудно получить
максимальное значение толщины льда, которое можно измерить без неоднозначности:
где С – скорость света в свободном пространстве. (Кстати, разработчики "Аквамарина" допустили неточность- удвоили эту величину.)
Точность измерений импульсным методом зависит от формы сигнала. Понятно, что минимальную погрешность можно ожидать, если в качестве зондирующего сигнала использовать импульс с пренебрежимо малой длительностью, т.е. сверхширокополосный сигнал. Однако, для измерения толщины льда и большинства земных покровов это невозможно.
Для оценки погрешностей радиолокационных станций проникающего зондирования (РЛСПЗ) была разработана цифровая имитационная модель. Зондирующие и отражённые сигналы дискретизированы на частоте F=f0N=1600 МГц, где N=64 - количество отсчётов. Моделировался полёт над дрейфующим морским льдом, толщина которого линейно изменялась в интервале 1…32 отсчёта. Цена одного отсчёта примерно 5 см. Оценивались относительные систематическая и среднеквадратичная погрешности измерения толщины льда. Отношение шум/сигнал равнялся нулю с погрешностью до точности вычислений.
Исследовалось три типа РЛСПЗ:
1. Импульсный цифровой измеритель толщины льда (ИТЛ) "Аквамарин", в котором функции оператора выполняла программа.
2. Импульсный ИТЛ с цифровой обработкой разности между отражённым и зондирующим сигналами.
3. Корреляционный ИТЛ.
На реальном "Аквамарине" толщину льда оценивает оператор, наблюдая один полный период отражённого сигнала на экране индикатора. Сигнал синхронизирован по максимуму-максиморуму, т. е. привязан к началу развёртки. Толщина льда определяется по положению второго максимума (первый находится в начале развёртки). Таким образом, априорно предполагается, что уровень отражённого сигнала от верхней поверхности всегда выше сигнала от нижней. Если же сигнал от нижней поверхности выше, то его максимум будет в начале развёртки и неизбежно возникнет ошибка при определении временного запаздывания
где Т – период
повторения импульсов,
![]() -
запаздывание сигнала от нижней поверхности относительно сигнала от верхней
поверхности. К сожалению, разработчики "Аквамарина" этой ошибки не
учли.
-
запаздывание сигнала от нижней поверхности относительно сигнала от верхней
поверхности. К сожалению, разработчики "Аквамарина" этой ошибки не
учли.
На малых толщинах льда, когда максимумы сигналов от верхней и нижней поверхностей льда неразличимы, толщина льда в "Аквамарине" оценивалась по увеличению длительности импульса. Очевидно, что эта оценка зависит от относительного уровня, на котором измеряется длительность импульса.
Алгоритм, моделирующий действия оператора, работает аналогичным образом. Вначале выполняется синхронизация по максимуму. Далее определяется положение второго максимума. Однако такой алгоритм не исключает ошибку неоднозначности (3), которая может быть значительной. Для её исключения отражённый сигнал преобразуется следующим образом
for(i=0; i<N/2; i++) y[i]+=y[N-i-1]; (4)
где y[i] – массив отсчётов отражённого сигнала. Здесь и далее используются операторы алгоритмического языка С++. Такое преобразование сигнала устанавливает диапазон измерения в соответствие с (2) и исключает ошибку неоднозначности (3).
Разностный РЛС ПЗ является возможной модернизацией цифрового "Аквамарина". Она сводится к следующему. Вначале зондирующий x[i] и отражённый y[i] сигналы синхронизируются по максимуму и преобразуются оператором (4). Далее оба сигнала приводятся к интервалу 0…1 оператором
for(i=0; i<N; i++) x[i]=(x[i]-xmin)/(xmax-xmin); (5)
где xmax, xmin – максимальное и минимальное значения отсчётов сигнала.
и формируется разностный сигнал r[i]:
for(i=0; i<N; i++) r[i]=y[i]-x[i]; (6)
Положение максимума-максиморума разностного сигнала r[i] на временной оси и пропорционально толщине слоя льда.
Принцип измерения корреляционной РЛС ПЗ состоит в том, что последовательно вычисляются коэффициенты взаимной корреляции отражённого и образцовых сигналов от льдов различной толщины, т. е. формируется функция правдоподобия (образцовые сигналы моделируются предварительно и записываются в память). Далее вычисляется апостериорное распределение и по положению его максимума-максиморума определяется толщина слоя льда.
Полученные на имитационной модели результаты приведены в таблицах 1 и 2 (для пресных речных и солёных дрейфующих морских льдов соответственно).
Таблица 1. Погрешность измерения толщины пресных речных льдов.
|
|
Тип сигнала |
Среднеквадратичная погрешность, % |
|||||
|
№ |
|
"Аквамарин" |
Разностный |
Корреляцион. |
|||
|
|
|
|
Cor |
|
Cor |
|
Cor |
|
1 |
Единичный импульс Кронекера |
1 |
0.993 |
2 |
0,999 |
0 |
1,000 |
|
2 |
Случайная последовательность |
|
-0,279 |
|
0,045 |
3 |
0,999 |
|
3 |
Колокольный импульс |
14 |
0,991 |
7 |
0,991 |
5 |
0,997 |
|
4 |
Синтезированный колокольный импульс из 6 синусоид |
15 |
0,989 |
6 |
0,994 |
5 |
0,996 |
|
5 |
Синтезированный колокольный импульс из 8 синусоид |
7 |
0,997 |
4 |
0,998 |
4 |
0.999 |
|
6 |
Сумма 6 синусоид минимально-фазовая |
|
0,233 |
5 |
0,996 |
4 |
0,998 |
|
7 |
Сумма 6 синусоид с нулевыми начальными фазами |
|
0,023 |
7 |
0,993 |
4 |
0,998 |
|
8 |
Сумма 6 синусоид со случайными начальными фазами |
|
-0,245 |
|
0,290 |
4 |
0,998 |
|
9 |
Сигнал "Аквамарина" |
43 |
0,853 |
6 |
0,996 |
14 |
0,969 |
|
10 |
Импульс Максвелла |
14 |
0.992 |
5 |
0,996 |
10 |
0,994 |
Значок "![]() " в таблице
означает полную невозможность измерения.
" в таблице
означает полную невозможность измерения.
Таблица 2. Погрешность измерения толщины солёных морских льдов.
|
№ |
Тип сигнала |
Среднеквадратичная погрешность, % |
|||||
|
|
|
"Аквамарин" |
Разностный |
Корреляцион. |
|||
|
|
|
|
Cor |
|
Cor |
|
Cor |
|
1 |
Единичный импульс Кронекера |
7 |
0.993 |
3 |
0,999 |
0 |
1,000 |
|
2 |
Случайная последовательность |
|
0,240 |
|
0,091 |
0 |
1,000 |
|
3 |
Колокольный импульс |
17 |
0.988 |
42 |
0,762 |
10 |
0,995 |
|
4 |
Синтезированный колокольный импульс из 6 синусоид |
17 |
0,988 |
41 |
0,776 |
7 |
0,996 |
|
5 |
Синтезированный колокольный импульс из 8 синусоид |
9 |
0,997 |
36 |
0,804 |
5 |
0.995 |
|
6 |
Сумма 6 синусоид минимально-фазовая |
|
-0,072 |
39 |
0,783 |
5 |
0,997 |
|
7 |
Сумма 6 синусоид с нулевыми начальными фазами |
|
0,103 |
7 |
0,993 |
4 |
0,998 |
|
8 |
Сумма 6 синусоид со случайными начальными фазами |
|
-0,391 |
|
0,074 |
5 |
0,997 |
|
9 |
Сигнал "Аквамарина" |
57 |
0,744 |
54 |
0,660 |
27 |
0,989 |
|
10 |
Импульс Максвелла |
18 |
0,988 |
42 |
0,763 |
10 |
0,992 |
Значок "![]() " в таблице
означает полную невозможность измерения.
" в таблице
означает полную невозможность измерения.
В этих таблицах приведены среднеквадратичные относительные погрешности измерения толщины льда d (в %) и коэффициенты взаимной корреляции между истинными и измеренными последовательностями - Cor .
Для моделирования использовалось десять зондирующих сигналов, которые можно разделить на две группы.
Сигналы первой группы (строки 1, 2, 3 таблиц) реализовать на практике можно только приблизительно, но они позволяют оценить потенциальные возможности того или иного метода обработки отражённых сигналов. Напомним - у импульса Кронекера только нулевой отсчёт равен единице, остальные - нулю.
Случайная последовательность формировалась датчиком равновероятных случайных чисел в интервале [-1,+1]:
Колокольный импульс
где
![]() - длительность импульса. В
пределах периода повторения колокольный импульс имеет только один максимум, что
для импульсных РЛСПЗ весьма важно: дополнительные максимумы затрудняют
интерпретацию отражённого сигнала.
- длительность импульса. В
пределах периода повторения колокольный импульс имеет только один максимум, что
для импульсных РЛСПЗ весьма важно: дополнительные максимумы затрудняют
интерпретацию отражённого сигнала.
Вторую группу сигналов (строки 4…10 таблиц) можно реализовать на практике. Известно два метода формирования зондирующего сигнала РЛСПЗ.
Первый: синтез из гармонических составляющих со специально подобранными частотами, амплитудами и фазами [4] (строки 4…9 таблиц):
где m – количество гармоник, N – количество отсчётов в сигнале.
Амплитуды и фазы для синтеза колокольных импульсов (строки 4 и 5 таблиц) подставляются в (9) из предварительно вычисленного спектра колокольного импульса (8). Эта операция подобна действиям оператора "Аквамарина" по подбору амплитуд и фаз при полёте над спокойной водной поверхностью, но её можно выполнять автоматически и наилучшим образом.
Сумма синусоид минимально-фазовая (строка 6 таблиц) состоит из синусоид с равными амплитудами, а её энергия наиболее плотно сконцентрирована около момента i=0. Сигнал содержит более одного максимума за период.
Суммы синусоид с нулевыми и случайными начальными фазами (строки 7 и 8 таблиц) особых пояснений не требуют. Они также содержат более одного максимума за период.
Сигнал "Аквамарина"
синтезирован. Амплитуды Ak для его синтеза по (9) задаются из
среднестатистического спектра реальных отражённых сигналов, полученных и
записанных во время лётных испытаний над льдами Северного Ледовитого океана, а
фазы как
![]() =0,392k+1,568
(см. рис.1). Подробнее о синтезе зондирующего сигнала на основе отражённых см.
в [5].
=0,392k+1,568
(см. рис.1). Подробнее о синтезе зондирующего сигнала на основе отражённых см.
в [5].
Другой способ формирования зондирующего сигнала: метод ударного возбуждения широкополосной антенны [3], как, например, в "Аквамарине". В этом случае зондирующий сигнал хорошо моделируется известным импульсом Максвелла
где ![]() - длительность импульса, k – относительная частота, i – отсчёты
времени, N - количество отсчётов сигнала. Длительность импульса выбрана
таким образом, что ширина спектра на уровне 0,1 содержит 7 гармоник с
частотами f=kf0=k25 МГц
(приём отражённого сигнала в "Аквамарине" выполнялся путём
синхронного детектирования именно на этих частотах).
- длительность импульса, k – относительная частота, i – отсчёты
времени, N - количество отсчётов сигнала. Длительность импульса выбрана
таким образом, что ширина спектра на уровне 0,1 содержит 7 гармоник с
частотами f=kf0=k25 МГц
(приём отражённого сигнала в "Аквамарине" выполнялся путём
синхронного детектирования именно на этих частотах).
На рис.2 серым цветом показан истинный профиль льда, а белым - профиль льда измеренный "Аквамарином" с зондирующим сигналом колоколообразной формы. Напомним: этот сигнал содержит только один максимум за период. Среднеквадратичная погрешность измерения 17%, коэффициент корреляции между истинным и измеренным профилями высокий - 0,988.
Рис. 2. Истинный (серый цвет) и измеренный (белый цвет) профили толщины льда. "Аквамарин" с колокольным импульсом.
Если в качестве зондирующего сигнала использовать сигнал "Аквамарина", то результаты существенно ухудшаются: погрешность возрастает до 57%, но коэффициент корреляции остаётся достаточно высоким – 0,774 (см. рис. 3). Причина в следующем. Амплитуды и фазы реального сигнала устанавливал оператор вручную. Полностью добиться желаемого он не смог – сигнал содержит более одного максимума (см. рис.1). Результат: в начале и конце диапазона наблюдаются сбои, вызванные тем, что отсчёт толщины льда производится не по сигналу, отражённому нижней поверхностью льда, а по вторичному максимуму. В середине диапазона измерение выполняется без сбоев. Даже относительно небольшое количество сбоев приводит к резкому увеличению погрешности, но коэффициент корреляции уменьшается при этом достаточно медленно.
Синтезированный из 6 синусоид минимально-фазовый зондирующий сигнал имеет явно выраженный второй максимум, поэтому измерение "Аквамарином" становится практически невозможным: коэффициент корреляции падает до пренебрежимо малого значения: -0,072 (см. рис.4).
Рис. 3. Истинный (серый цвет) и измеренный (белый цвет) профили толщин льда. "Аквамарин" с реальным сигналом "Аквамарина".
Рис. 4. Истинный (серый цвет) и измеренный (белый цвет) профили толщин льда. "Аквамарин" с синтезированным из 6 синусоид минимально фазовым сигналом.
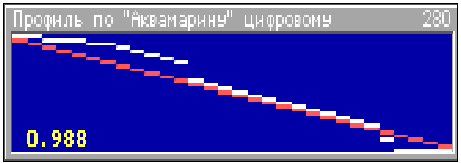
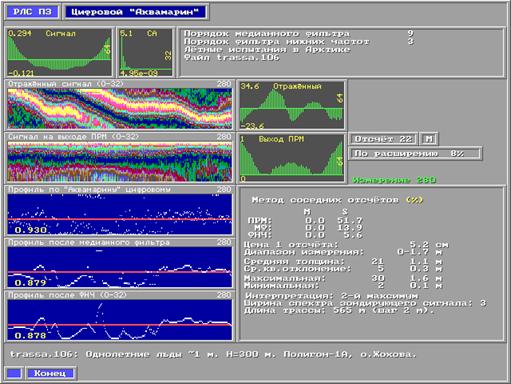
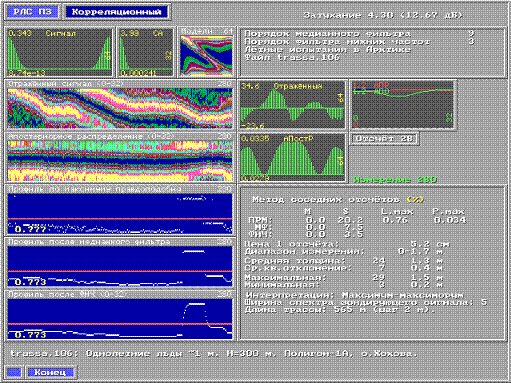
Для сравнения приведём результаты обработки записанных отражённых сигналов "Аквамарина" во время натурных лётных испытаний над дрейфующими льдами Северного Ледовитого океана. На рис.5 показан профиль, полученный "Аквамарином", а на рис.6, профиль, полученный путём корреляционной обработки этих же сигналов. На нём хорошо просматривается стык двух ледяных полей в конце трассы и разводье. Среднеквадратичная погрешность во время лётных испытаний оценивалась методом соседних отсчётов [1]. Для приведенного отрезка трассы, длиной около 600 м (280 отсчётов толщины льда с шагом 2 м), погрешность "Аквамарина" составляет примерно 52%, а на этом же участке трассы погрешность корреляционного ИТЛ – 20%. Разница существенная. Разностная обработка снизила погрешность до 46% (в целях экономии места рисунок не приводим).
В таблице 3 показаны результаты, полученные после вторичной обработки профилей путём медианной и низкочастотной фильтрации.
Таблица 3. Погрешность измерений толщины льда в районе о. Жохова.
|
|
Среднеквадратичная погрешность, % |
||
|
|
"Аквамарин" |
Разностный |
Корреляционный |
|
Исходный профиль |
51 |
46 |
20 |
|
Профиль после медианной фильтрации |
14 |
10 |
8 |
|
Профиль после низкочастотной фильтрации |
6 |
5 |
4 |
Рис. 5. Профиль толщин льда в районе острова Жохова, полученный на "Аквамарине"
Рис. 6. Профиль толщин льда в районе острова Жохова, полученный путём корреляционной обработки.
Полученные результаты позволяют сделать следующие выводы:
§ Погрешность измерения толщины слоистых сред импульсных РЛСПЗ сильно зависит от формы зондирующего сигнала. Минимальную погрешность обеспечивает сигнал с одним максимумом за период повторения. Дополнительные максимумы приводят к неопределённости и вызывают сбои. Неправдоподобные значения, возникающие в результате этих сбоев, вызывают значительные трудности при последующем анализе. Для устранения неправдоподобных значений предложено немало алгоритмов автоматического редактирования (мы использовали медианную и низкочастотную фильтрацию), но ни один из них не является полностью удовлетворительным.
§ Погрешность измерения корреляционной РЛСПЗ практически не зависит от формы зондирующего сигнала. Наименьшую погрешность позволяют получить сигналы, имеющие равномерный спектр амплитуд. Спектр фаз на точность измерений не влияет.
§ Погрешность измерения РЛСПЗ всех рассмотренных типов уменьшается с увеличением ширины спектра зондирующего сигнала. При зондировании дисперсных сред, например, солёного морского льда, увеличение ширины спектра зондирующего сигнала и связанное с этим уменьшение погрешности имеет предел.
§ Для корреляционной РЛСПЗ целесообразно зондирующий сигнал синтезировать из синусоид с примерно одинаковыми амплитудами и произвольными, но когерентными начальными фазами.
§ Для импульсных РЛСПЗ целесообразно синтезировать зондирующий сигнал колоколообразной формы. Однако, поскольку реальная антенно-фидерная система значительно искажает зондирующий сигнал (особенно в метровом диапазоне волн), необходимо вводить коррекцию амплитуд и фаз. Для этого можно использовать сигнал, отражённый спокойной поверхностью моря. В "Аквамарине" эту операцию выполняет оператор, но не лучшим образом. Однако, имея сигнал, отражённый морской поверхностью, нетрудно автоматически синтезировать обратный фильтр, на выходе которого будет сигнал колоколообразной формы, обеспечивающий минимум погрешности.
ЛИТЕРАТУРА
1. В.В.Богородский, А.Г.Оганесян. Проникающая радиолокация морских льдов с цифровой обработкой информации.-С.Петербург: Гидрометеоиздат, 1987, 342 с.
2. М.И.Финкельштейн, В.Л.Мендельсон, В.А.Кутев. Радиолокация слоистых земных покровов.-М.: Советское радио, 1977, 174 с.
3. Cook J. C. Proposed monocycle-pulse VHP radar for airborne ice and snow measurement. – Trans. Amer. IEE, pt. 1. Commun. and Electronic, 1960, vol. 79, p. 588-594.
4. Робинсон Л. А., Уэйр У. Б., Юнг Г. Л. Установление местоположения и распознавание неоднородностей в диэлектрических средах с помощью синтезируемых ВЧ-импульсов. – Труды института инженеров электротехники и радиоэлектроники, США, 1974, т. 62, с. 42-52.
5. Ю.Д.Добуш, О.П.Козевич, Е.Ф.Накалов, А.Г.Оганесян. Корреляционная цифровая обработка радиолокационных сигналов при измерении толщины морских льдов. – Автометрия, № 6, 1989, с.40-45.
Авторы:
Альберт Георгиевич ОГАНЕСЯН
Доктор физико-математических наук, профессор, Государственный университет "Львовская политехника",
e-mail: oganes@polynet.lviv.ua;
Игорь Борисович ЧАЙКОВСКИЙ
Государственный университет "Львовская политехника", заведующий лабораторией.