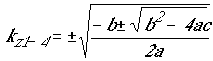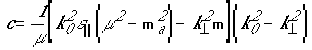|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 8, 2002 |
|
ПРЯМЫЕ И ОБРАТНЫЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В КОМПОЗИЦИОННОЙ СРЕДЕ, СОСТОЯЩЕЙ ИЗ МАГНИТНЫХ И ЭЛЕКТРИЧЕСКИХ ЭЛЕМЕНТОВ
В.И.Щеглов
Институт радиотехники и электроники РАН
Получена 5 августа 2002 г.
Предложена модель композиционной среды, состоящей из двух вложенных друг в друга решеток кубической симметрии, в узлах одной из которых расположены ферритовые сферы, а другой - электрические диполи с сосредоточенной индуктивностью. Получено дисперсионное соотношение для произвольного направления распространения электромагнитных волн в такой среде, построены изочастотные кривые и выявлены условия существования прямых и обратных волн.
Возможность аналоговой обработки сигналов СВЧ диапазона (0,1-100 ГГц) с помощью устройств на ферритах [1,2] обусловлена явлением ферромагнитного резонанса (ФМР), состоящем в резонансном отклике собственных колебаний среды на переменное магнитное поле [3]. С другой стороны, если бы имелась среда, реагирующая в том же диапазоне резонансным образом еще и на переменное электрическое поле, то сочетание резонансных магнитных и электрических свойств могло бы значительно расширить возможности устройств. Действительно, резонансное поведение магнитной или диэлектрической проницаемости среды предполагает в некоторой частотной области вблизи резонанса изменение ее знака с положительного на отрицательный. Если частоты магнитного и электрического резонансов близки, то в их окрестности возможны условия, при которых как магнитная, так и диэлектрическая проницаемости становятся отрицательными одновременно. В работах [4,5] показано, что при этом в среде могут распространяться обратные волны, свойства которых отличны от свойств прямых волн, то есть появляется возможность реализовать новые принципы создания устройств.
Прекрасную иллюстрацию богатства физических свойств обратных волн дают обратные магнитостатические волны, существующие в ферритовых пленках и структурах феррит-диэлектрик-металл [6-10]. На характере этих волн, благодаря их магнитостатической природе, диэлектрические свойства среды практически никак не сказываются. Естественно ожидать, что добавление к магнитным еще и электрических резонансных свойств внесет новое разнообразие в картину явлений.
Однако, к сожалению, естественные среды, обладающие одинаково сильно выраженными магнитными и электрическими резонансными свойствами в одном и том же диапазоне, в настоящее время не известны. Такое положение побуждает искать возможность создания искусственных композиционных сред, выполненных на основе набора дискретных элементов. Так, в работах [11,12] описана среда с одновременно отрицательными значениями магнитной и диэлектрической проницаемостей, выполненная на основе металлических проводящих элементов, а в работе [13] приведены результаты экспериментального наблюдения обратных волн в ферритовой пластине, на поверхности которой расположена решетка из параллельных металлических проводников, трактуемая авторами как среда с отрицательной диэлектрической проницаемостью. Однако, параметры среды из проводящих элементов [11,12] неизменны, то есть среда неуправляема, а описанная в работе [13] среда состоит их двух пластин (магнитной пластины и решетки из проводников), то есть является заведомо планарной (двухмерной) и пространственно неоднородной.
С другой стороны, введение ферритов в композиционную среду обеспечивает возможность управления ее параметрами, а проводящие элементы дают отрицательное значение диэлектрической проницаемости, то есть в трехмерной среде, содержащей ферритовые и проводящие элементы возможно распространение обратных волн. свойствами которых можно управлять, меняя магнитное поле.
Ранее мы уже предлагали модель трехмерной управляемой композиционной среды, состоящей из двух вложенных друг в друга решеток кубической симметрии, в узлах одной из которых расположены ферритовые сферы, а другой - электрические диполи с сосредоточенной индуктивностью [14-16]. Были выявлены условия, при которых магнитная и диэлектрическая проницаемости такой среды одновременно принимают отрицательные значения, что дает возможность распространения обратных волн. Настоящая работа посвящена более подробному исследованию этого вопроса.
2. ПОСТАНОВКА ЗАДАЧИ. ПАРАМЕТРЫ СРЕДЫ.
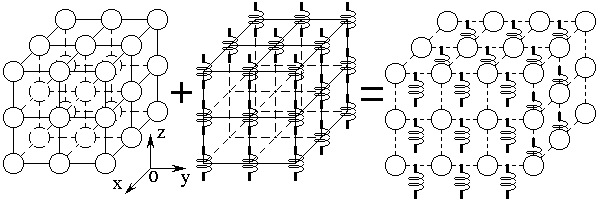
Схема композиционной среды показана на рис.1. Среда содержит две соосно
вложенные друг в друга одинаковые решетки из повторяющихся элементов, имеющие
кубическую симметрию с длиной ребра ячейки равной ![]() . В узлах одной решетки расположены
ферритовые сферы, намагниченные однородным постоянным полем, а в узлах другой -
одинаково ориентированные электрические диполи. Каждый диполь представляет
собой прямой отрезок проводника с включенной посередине проволочной катушкой,
играющей роль сосредоточенной индуктивности. Плоскость витков катушки
перпендикулярна проводнику диполя. Направление прямых участков проводников
диполей совпадает с направлением постоянного магнитного поля. Для простоты
будем считать, что это направление параллельно одному из ребер кубических
решеток среды. Длина диполей,
. В узлах одной решетки расположены
ферритовые сферы, намагниченные однородным постоянным полем, а в узлах другой -
одинаково ориентированные электрические диполи. Каждый диполь представляет
собой прямой отрезок проводника с включенной посередине проволочной катушкой,
играющей роль сосредоточенной индуктивности. Плоскость витков катушки
перпендикулярна проводнику диполя. Направление прямых участков проводников
диполей совпадает с направлением постоянного магнитного поля. Для простоты
будем считать, что это направление параллельно одному из ребер кубических
решеток среды. Длина диполей,
Рис.1. Схема устройства композиционной среды.
диаметр катушек и ферритовых сфер значительно меньше длины ребра ячейки решетки. Отдельные элементы каждой решетки считаются не взаимодействующими друг с другом. В описанном виде обе решетки обладают резонансными свойствами: частота резонанса ферритовых сфер определяется параметрами феррита и приложенным магнитным полем, а частота диполей - их длиной и индуктивностью катушек.
Основной задачей настоящей работы является исследование свойств электромагнитных волн (ЭМВ), распространяющихся в такой среде. Предположим, что длина ЭМВ значительно превышает размер ячейки решетки. При этом, благодаря отсутствию взаимодействия между элементами решеток, анизотропные свойства среды определяются не кубической симметрией решеток, а анизотропными свойствами отдельного ее элемента. Поэтому можно считать, что среда обладает одноосной анизотропией, ось которой совпадает с направлением магнитного поля и прямых участков проводников диполей.
Выберем систему координат ![]() такую, в которой ось
такую, в которой ось ![]() параллельна оси анизотропии
среды, то есть направлению магнитного поля и прямых участков проводников
диполей (рис.1). При этом плоскость
параллельна оси анизотропии
среды, то есть направлению магнитного поля и прямых участков проводников
диполей (рис.1). При этом плоскость ![]() перпендикулярна оси
перпендикулярна оси ![]() и параллельна плоскостям
расположения элементов решеток, а также плоскости витков катушек диполей. На
рис.1 оси
и параллельна плоскостям
расположения элементов решеток, а также плоскости витков катушек диполей. На
рис.1 оси ![]() и
и ![]() совпадают с
направлениями ребер кубической решетки среды, но это совпадение для дальнейшего
рассмотрения значения не имеет.
совпадают с
направлениями ребер кубической решетки среды, но это совпадение для дальнейшего
рассмотрения значения не имеет.
Предположим, что действующее на ферритовые сферы переменное магнитное поле
значительно меньше приложенного постоянного поля, а поперечные размеры диполя
вместе с катушкой (в плоскости ![]() ) малы по сравнению с его длиной (вдоль оси
) малы по сравнению с его длиной (вдоль оси
![]() ). При таких
условиях активно взаимодействовать со средой может только переменное магнитное
поле, вектор которого ориентирован в плоскости
). При таких
условиях активно взаимодействовать со средой может только переменное магнитное
поле, вектор которого ориентирован в плоскости ![]() , то есть имеет компоненты
, то есть имеет компоненты ![]() и
и ![]() , а также переменное
электрическое поле, вектор которого параллелен оси
, а также переменное
электрическое поле, вектор которого параллелен оси ![]() , то есть имеет лишь одну
компоненту
, то есть имеет лишь одну
компоненту ![]() .
Все остальные компоненты электрического и магнитного полей, а именно:
.
Все остальные компоненты электрического и магнитного полей, а именно: ![]() ,
, ![]() и
и ![]() с элементами среды не взаимодействуют.
с элементами среды не взаимодействуют.
Воспользуемся результатами наших более ранних работ [15,16], где вычислены
тензоры магнитной и диэлектрической проницаемостей исследуемой среды.
Пренебрежем затуханием и нормируем все величины на магнитные параметры среды:
поля и индукции - на ![]() ,
а частоты - на
,
а частоты - на ![]() .
При временной зависмости
.
При временной зависмости ![]() для подрешетки из ферритовых сфер радиуса
для подрешетки из ферритовых сфер радиуса ![]() получаем магнитную
проницаемость в виде:
получаем магнитную
проницаемость в виде:
где:
причем:
![]() - постоянное поле,
- постоянное поле, ![]() - гиромагнитное
отношение,
- гиромагнитное
отношение, 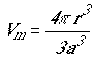 -
коэффициент заполнения пространства магнитными сферами.
-
коэффициент заполнения пространства магнитными сферами.
Для подрешетки из электрических диполей длины ![]() получаем тензор диэлектрической
проницаемости в виде:
получаем тензор диэлектрической
проницаемости в виде:
в котором:
где
по аналогии с магнитной проницаемостью введен коэффициент заполнения
пространства диполями: 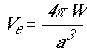 , причем:
, причем: 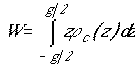 - дипольный момент одного диполя,
- дипольный момент одного диполя,
![]() - частота собственных
колебаний диполя,
- частота собственных
колебаний диполя, ![]() -
эффективная емкость диполя,
-
эффективная емкость диполя, ![]() - его эффективная индуктивность,
- его эффективная индуктивность, ![]() - линейная плотность
зарядов в проводнике диполя, нормированная на амплитуду напряженности
электрического поля.
- линейная плотность
зарядов в проводнике диполя, нормированная на амплитуду напряженности
электрического поля.
В пределах длины диполя ![]() можно приближенно представить в виде ряда:
можно приближенно представить в виде ряда:
где:
![]() ,
, ![]() , ...
, ...![]() - постоянные величины,
- постоянные величины, ![]() - целое.
- целое.
Коэффициенты
ряда можно определить численно из условия равенства нулю поля внутри
проводника. Вне проводника очевидно ![]() . Представляя пространство, занимаемое
одним диполем в виде эквивалентной сферы, можно найти “эффективный радиус
диполя” в виде:
. Представляя пространство, занимаемое
одним диполем в виде эквивалентной сферы, можно найти “эффективный радиус
диполя” в виде:
Численные оценки показывают, что по порядку величины эффективный радиус диполя близок к половине его длины.
Аналогично [15,16], емкость отдельного диполя можно определить, найдя поле, создаваемое зарядами, наводимыми в проводнике диполя внешним полем. При этом получаем:
Для расчета индуктивности катушки диполя предположим, что по ее проводнику течет ток и найдем сначала поле и магнитный поток одного витка, откуда определим его индуктивность, после чего результат умножим на число витков. В результате получаем индуктивность катушки в виде:
Здесь
![]() - полярная
координата на плоскости витка,
- полярная
координата на плоскости витка, ![]() - азимутальная координата контура витка,
- азимутальная координата контура витка, ![]() - радиус витка,
- радиус витка, ![]() - диаметр его провода,
- диаметр его провода, ![]() - число витков катушки.
- число витков катушки.
3. ИЗМЕНЕНИЕ МАГНИТНОЙ И ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТЕЙ С ЧАСТОТОЙ.
Рассмотрим теперь зависимости компонент тензоров магнитной и диэлектрической
проницаемостей (1) и (4) от нормированной частоты ![]() . Аналитический вид этих зависимостей
дается формулами (2) и (5), а соответствующие кривые, построенные для
резонансных частот
. Аналитический вид этих зависимостей
дается формулами (2) и (5), а соответствующие кривые, построенные для
резонансных частот ![]() =
1,00 и
=
1,00 и ![]() = 0,90
и коэффициентов заполнения
= 0,90
и коэффициентов заполнения ![]() =
= ![]() = 0,25, представлены на рис.2.
= 0,25, представлены на рис.2.
Рис.2. Зависимости компонент тензоров проницаемостей от частоты.
Сплошной
линией здесь показана зависимость ![]() , пунктирными - зависимости
, пунктирными - зависимости ![]() и
и ![]() . Из рис.2 можно видеть, что
компонента
. Из рис.2 можно видеть, что
компонента ![]() ,
при
,
при ![]() равная
равная 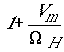 , при увеличении
, при увеличении ![]() увеличивается, стремясь
при
увеличивается, стремясь
при ![]() к
к ![]() , после чего меняет
знак, переходя на
, после чего меняет
знак, переходя на ![]() ,
затем, снова увеличиваясь, проходит через нуль при
,
затем, снова увеличиваясь, проходит через нуль при ![]() , после чего, оставаясь
положительной, стремится к единице. Таким образом,
, после чего, оставаясь
положительной, стремится к единице. Таким образом, ![]() является отрицательной в
интервале частот:
является отрицательной в
интервале частот: ![]() .
Аналогично можно убедиться, что
.
Аналогично можно убедиться, что ![]() положительна при
положительна при ![]() , стремится к
, стремится к ![]() вблизи
вблизи ![]() и отрицательна при
и отрицательна при ![]() .
.
Единственная зависящая от частоты компонента тензора диэлектрической
проницаемости ![]() при
при
![]() равна:
равна: ![]() . При увеличении частоты
. При увеличении частоты
![]() увеличивается
и при
увеличивается
и при ![]() стремится
к
стремится
к ![]() . При
. При ![]() величина
величина ![]() расходится и меняет
знак: переходит с
расходится и меняет
знак: переходит с ![]() на
на
![]() . При
дальнейшем увеличении
. При
дальнейшем увеличении ![]() величина
величина
![]() , будучи
отрицательной, снова увеличивается, затем при
, будучи
отрицательной, снова увеличивается, затем при ![]() , где
, где ![]() , проходит через нуль, меняет знак на
положительный и, слегка увеличиваясь, при
, проходит через нуль, меняет знак на
положительный и, слегка увеличиваясь, при ![]() стремится к единице. Таким образом,
стремится к единице. Таким образом, ![]() является отрицательной
в интервале частот:
является отрицательной
в интервале частот: ![]() .
.
Из приведенных формул видно, что интервалы частот, где диэлектрическая и
магнитная проницаемости принимают отрицательные значения, сильно зависят от
коэффициентов заполнения среды диполями и магнитными сферами (![]() и
и ![]() ). Ширина этих интервалов
максимальна при
). Ширина этих интервалов
максимальна при ![]() и
и
![]() и
приближается к аналогичной ширине для сплошной среды, а в случае
и
приближается к аналогичной ширине для сплошной среды, а в случае ![]() и
и ![]() она стремится к нулю.
она стремится к нулю.
Резюмируя сказанное, можно заключить, что вблизи резонансной частоты отдельного
диполя ![]() поведение
диэлектрической проницаемости аналогично поведению магнитной проницаемости
вблизи частоты ферромагнитного резонанса
поведение
диэлектрической проницаемости аналогично поведению магнитной проницаемости
вблизи частоты ферромагнитного резонанса ![]() , то есть имеются области частот, в
которых, как та, так и другая проницаемости отрицательны, причем ширина этих
областей тем больше, чем больше коэффициенты заполнения среды диполями и
сферами. Частотная зависимость диэлектрической проницаемости определяется
только параметрами решетки и составляющих ее диполей, то есть неизменна.
Напротив, частотная зависимость магнитной проницаемости определяется не только
параметрами ферритовых элементов, но также и приложенным магнитным полем, меняя
которое, магнитной проницаемостью можно управлять, то есть при надлежащем
выборе магнитного поля можно обеспечить условия для распространения в среде
обратных волн.
, то есть имеются области частот, в
которых, как та, так и другая проницаемости отрицательны, причем ширина этих
областей тем больше, чем больше коэффициенты заполнения среды диполями и
сферами. Частотная зависимость диэлектрической проницаемости определяется
только параметрами решетки и составляющих ее диполей, то есть неизменна.
Напротив, частотная зависимость магнитной проницаемости определяется не только
параметрами ферритовых элементов, но также и приложенным магнитным полем, меняя
которое, магнитной проницаемостью можно управлять, то есть при надлежащем
выборе магнитного поля можно обеспечить условия для распространения в среде
обратных волн.
Рассмотрим теперь распространение электромагнитных волн (ЭМВ) в изучаемой
среде. Полагая пространственно-временную зависимость волны в виде: ![]() , для безграничной
среды с тензорными параметрами аналогично [3,15] получаем дисперсионное
соотношение:
, для безграничной
среды с тензорными параметрами аналогично [3,15] получаем дисперсионное
соотношение:
где
параметры ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() определяются конкретными свойствами среды
и для тензоров проницаемостей вида (1) и (4) принимают вид:
определяются конкретными свойствами среды
и для тензоров проницаемостей вида (1) и (4) принимают вид:
![]() ,
, 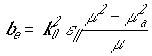 ,
, 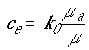 ,
,
причем:
![]() , а
, а ![]() - скорость света.
- скорость света.
Учитывая осевую (относительно ![]() ) симметрию задачи, для дальнейшего
рассмотрения удобно ввести поперечное волновое число
) симметрию задачи, для дальнейшего
рассмотрения удобно ввести поперечное волновое число ![]() , в результате чего соотношение
(12) принимает вид:
, в результате чего соотношение
(12) принимает вид:
Это
дисперсионное соотношение легко разрешается относительно ![]() :
:
где:
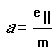 ,
, 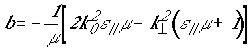 ,
,
Решение
(14)-(15) дисперсионного уравнения (13) описывает четыре волны,
распространяющиеся в полном пространстве ![]() . В силу симметрии задачи относительно
плоскости
. В силу симметрии задачи относительно
плоскости ![]() ,
два знака перед внешним корнем в выражении (14) описывают две пары волн,
свойства которых с точностью до симметрии совпадают. Два знака перед внутренним
корнем в том же выражении описывают внутри каждой пары две принципиально различных
волны, свойства которых - длина и направление векторов фазовой и групповой
скоростей, а также прямой или обратный характер могут коренным образом
различаться.
,
два знака перед внешним корнем в выражении (14) описывают две пары волн,
свойства которых с точностью до симметрии совпадают. Два знака перед внутренним
корнем в том же выражении описывают внутри каждой пары две принципиально различных
волны, свойства которых - длина и направление векторов фазовой и групповой
скоростей, а также прямой или обратный характер могут коренным образом
различаться.
Рассмотрим сначала некоторые частные случаи распространения волн, а именно, когда волновой вектор перпендикулярен и параллелен оси анизотропии среды. В обоих этих случаях направления векторов фазовой и групповой скоростей распространяющихся волн совпадают, но знаки могут быть различны.
5. ВОЛНОВОЙ ВЕКТОР ПЕРПЕНДИКУЛЯРЕН ОСИ АНИЗОТРОПИИ СРЕДЫ.
Пусть волновой вектор волны перпендикулярен оси анизотропии среды, то есть ![]() ,
, ![]() . При этом дисперсионное
соотношение (13) принимает вид:
. При этом дисперсионное
соотношение (13) принимает вид:
то есть распадается на два независимых соотношения:
и
разрешая
которые относительно ![]() и
вводя аналогично [3] обозначение:
и
вводя аналогично [3] обозначение: 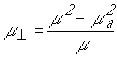 , получаем:
, получаем:
В этих соотношениях роль двух знаков аналогична отмеченной для выражения (14),
поэтому далее их опускаем. Анализ структуры волновых полей показывает, что в
плоскости ![]() в
среде возможно распространение двух не связанных между собою волн, отличающихся
поляризацией. Для первой волны, описываемой соотношением (19), отличны от нуля
компоненты полей
в
среде возможно распространение двух не связанных между собою волн, отличающихся
поляризацией. Для первой волны, описываемой соотношением (19), отличны от нуля
компоненты полей ![]() ,
,
![]() и
и ![]() . Ранее [15,16]
аналогичную волну мы назвали “гиромагнитной”. Необходимым условием
распространения этой волны является действительность
. Ранее [15,16]
аналогичную волну мы назвали “гиромагнитной”. Необходимым условием
распространения этой волны является действительность ![]() , что дает:
, что дает: ![]() . Возможны два варианта
выполнения этого неравенства:
. Возможны два варианта
выполнения этого неравенства:
1)
![]() и
и ![]() . Этот случай
соответствует прямой волне.
. Этот случай
соответствует прямой волне.
2)
![]() и
и ![]() . Этот случай
соответствует обратной волне.
. Этот случай
соответствует обратной волне.
Вторая волна, описываемая соотношением (20), имеет отличные от нуля компоненты
полей ![]() ,
, ![]() и
и ![]() и со средой никак не
взаимодействует, то есть тождественна прямой электромагнитной волне в пустом
пространстве.
и со средой никак не
взаимодействует, то есть тождественна прямой электромагнитной волне в пустом
пространстве.
Рассмотрим условия существования прямых и обратных волн, исходя из вида
тензоров проницаемостей (1) и (4), компоненты которых определяются формулами
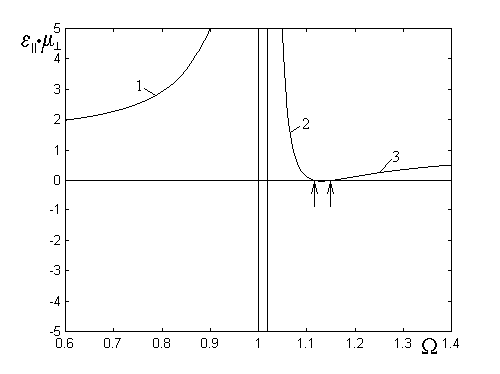
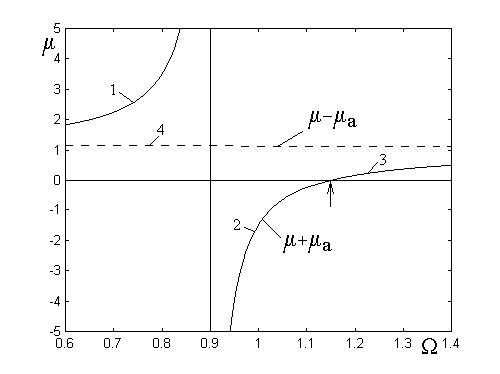
(2) и (5). Эти условия иллюстрируются
рис.3, где приведена зависимость от
частоты величины ![]() .
.
Рис.3. Зависимость величины ![]() от частоты.
от частоты.
Из рисунка видно, что ![]() в
интервалах частот:
в
интервалах частот: ![]() (кривая
1),
(кривая
1), ![]() (кривая
2) и
(кривая
2) и ![]() (кривая
3). Только в этих интервалах в среде возможно распространение волн, причем в
крайних по частоте интервалах (1,3)
(кривая
3). Только в этих интервалах в среде возможно распространение волн, причем в
крайних по частоте интервалах (1,3)![]() и
и ![]() , то есть волны прямые, а в среднем (2) -
, то есть волны прямые, а в среднем (2) -![]() и
и ![]() , то есть волны обратные.
Аналогично
, то есть волны обратные.
Аналогично ![]() в
интервалах частот:
в
интервалах частот: ![]() (между
кривыми 1 и 2), а также
(между
кривыми 1 и 2), а также ![]() (между кривыми 2 и 3). Распространение
волн в этих интервалах невозможно. Границы интервалов определяются частотами,
где составляющие произведения
(между кривыми 2 и 3). Распространение
волн в этих интервалах невозможно. Границы интервалов определяются частотами,
где составляющие произведения ![]() расходятся или равны нулю. При принятых
ранее значениях параметров (
расходятся или равны нулю. При принятых
ранее значениях параметров (![]() = 1,00,
= 1,00, ![]() = 0,90,
= 0,90, ![]() =
= ![]() = 0,25), получаем:
= 0,25), получаем: ![]() = 1,0173;
= 1,0173; ![]() =1,1180;
=1,1180; ![]() =1,1500.
=1,1500.
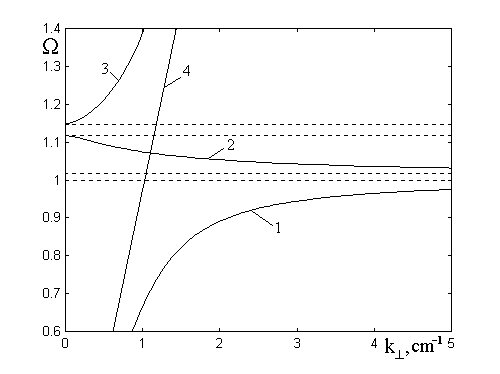
Рис.4. Дисперсионные кривые при ![]() .
.
На рис.4 приведены дисперсионные зависимости, построенные по формулам (19)
(кривые 1-3) и (20) (кривая 4). Видно, что для дисперсионного соотношения (19)
наклон кривых 1 и 3, соответствующих интервалам ![]() и
и ![]() , положителен, то есть эти волны прямые, а
наклон кривой 2, соответствующей интервалу
, положителен, то есть эти волны прямые, а
наклон кривой 2, соответствующей интервалу ![]() , отрицателен, то есть эти волны обратные.
Для дисперсионного соотношения (20) наклон кривой 4 всегда положителен, то есть
эти волны всегда прямые.
, отрицателен, то есть эти волны обратные.
Для дисперсионного соотношения (20) наклон кривой 4 всегда положителен, то есть
эти волны всегда прямые.
6. ВОЛНОВОЙ ВЕКТОР ПАРАЛЛЕЛЕН ОСИ АНИЗОТРОПИИ СРЕДЫ.
Рассмотрим теперь случай, когда волновой вектор параллелен оси анизотропии
среды, то есть ![]() ,
,
![]() . При этом
дисперсионное соотношение (13) принимает вид:
. При этом
дисперсионное соотношение (13) принимает вид:
Разрешая
(21) относительно ![]() ,
получаем:
,
получаем:
В этих выражениях подобно (19)-(20) знаки можно опустить. Анализ структуры
волновых полей показывает, что в среде могут распространяться две независимые
чисто поперечные волны, все поля которых лежат в плоскости ![]() . В каждой волне присутствует
вращающееся по кругу как магнитное, так и электрическое поле, причем в первой
волне, соответствующей (22) это вращение правое, тогда как во второй волне,
соответствующей (23) это вращение левое. Поскольку электрические поля волн
обеих типов перпендикулярны прямым участкам диполей, то электрические элементы
среды (диполи) в распространении этих волн никак не участвуют и аналогичные
волны могут распространяться в среде, состоящей только из магнитных сфер (без
решетки из диполей). Необходимым условием распространения этих волн является
действительность
. В каждой волне присутствует
вращающееся по кругу как магнитное, так и электрическое поле, причем в первой
волне, соответствующей (22) это вращение правое, тогда как во второй волне,
соответствующей (23) это вращение левое. Поскольку электрические поля волн
обеих типов перпендикулярны прямым участкам диполей, то электрические элементы
среды (диполи) в распространении этих волн никак не участвуют и аналогичные
волны могут распространяться в среде, состоящей только из магнитных сфер (без
решетки из диполей). Необходимым условием распространения этих волн является
действительность ![]() ,
что требует выполнения неравенств:
,
что требует выполнения неравенств:![]() или
или![]() , причем в обоих случаях волны являются
прямыми.
, причем в обоих случаях волны являются
прямыми.
Условия существования волн иллюстрируются рис.5, где приведена зависимость от
частоты величин![]() (кривые 1-3) и
(кривые 1-3) и![]() (кривая 4). Из рисунка видно, что
(кривая 4). Из рисунка видно, что ![]() (то есть выполняется дисперсионное
соотношение (22)) в интервалах частот:
(то есть выполняется дисперсионное
соотношение (22)) в интервалах частот: ![]() (кривая 1) и
(кривая 1) и ![]() (кривая 3), а
(кривая 3), а ![]() (то есть выполняется
дисперсионное соотношение (23)) - всегда при
(то есть выполняется
дисперсионное соотношение (23)) - всегда при ![]() (кривая 4).
(кривая 4).
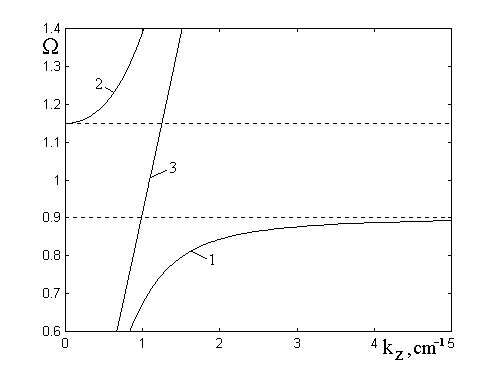
На рис.6 показаны соответствующие дисперсионные кривые: для соотношения (22) - кривые 1 и 2, а для соотношения (23) - кривая 3. Из рисунка видно, что наклон всех кривых положителен, то есть все волны, описываемые соотношениями (22) и (23) - прямые.
Рис.5. Зависимости величин ![]() и
и ![]() от частоты.
от частоты.
Рис.6. Дисперсионные кривые при ![]() .
.
7. ПРОИЗВОЛЬНОЕ НАПРАВЛЕНИЕ ВОЛНОВОГО ВЕКТОРА.
Рассмотрим теперь случай произвольного направления волнового вектора. В силу
симметрии достаточно рассмотреть лишь распространение волн в плоскости,
проходящей через ось симметрии ![]() . При этом все направления в плоскости
. При этом все направления в плоскости ![]() будут эквивалентными и
для их единообразного описания будем использовать введенное ранее поперечное
волновое число
будут эквивалентными и
для их единообразного описания будем использовать введенное ранее поперечное
волновое число ![]() .
Благодаря симметрии системы относительно плоскости
.
Благодаря симметрии системы относительно плоскости ![]() , достаточно рассмотреть лишь
случай
, достаточно рассмотреть лишь
случай ![]() и
и ![]() . Дисперсионное
соотношение в этом случае имеет вид (13) или в разрешенном относительно
. Дисперсионное
соотношение в этом случае имеет вид (13) или в разрешенном относительно ![]() виде - (14). Для такого
двухмерного случая удобным средством анализа распространения волн в произвольном
направлении являются изочастотные кривые [17], в данном случае рассматриваемые
в плоскости
виде - (14). Для такого
двухмерного случая удобным средством анализа распространения волн в произвольном
направлении являются изочастотные кривые [17], в данном случае рассматриваемые
в плоскости ![]() .
Трехмерные изочастотные поверхности в пространстве
.
Трехмерные изочастотные поверхности в пространстве ![]() получаются из двухмерных путем
их вращения вокруг оси
получаются из двухмерных путем
их вращения вокруг оси ![]() . На плоскости
. На плоскости ![]() уравнения изочастотных кривых
уравнения изочастотных кривых ![]() имеют вид (14) с
учетом (15), а также (2) и (5).
имеют вид (14) с
учетом (15), а также (2) и (5).
8. ВОЗМОЖНОСТЬ СУЩЕСТВОВАНИЯ ОБРАТНЫХ ВОЛН.
Рассмотрим теперь возможность существования обратных волн в такой системе. Для
иллюстрации возьмем частоту ![]() = 1,05, которой при
= 1,05, которой при ![]() соответствует прямая волна с
соответствует прямая волна с ![]() = 1,076 см-1
и обратная с
= 1,076 см-1
и обратная с ![]() =
2,334 см-1. (рис.4), а при
=
2,334 см-1. (рис.4), а при ![]() - только прямая волна с
- только прямая волна с ![]() = 1,143 см-1
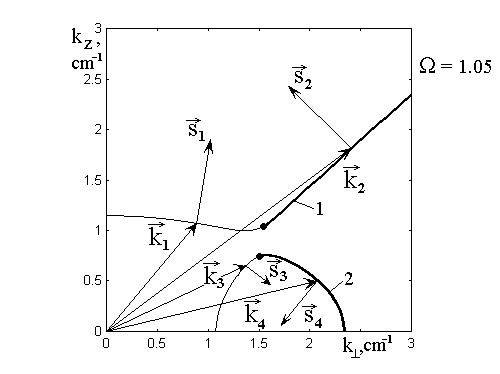
(рис.6). Построенные по (14) изочастотные кривые показаны на
рис.7 (кривые 1 и
2). Там же показаны волновые
= 1,143 см-1
(рис.6). Построенные по (14) изочастотные кривые показаны на
рис.7 (кривые 1 и
2). Там же показаны волновые ![]() и лучевые
и лучевые ![]() векторы для различных участков этих кривых.
Волновые векторы начинаются в начале координат и заканчиваются на изочастотной
кривой. Каждый лучевой вектор перпендикулярен касательной к изочастотной кривой
в точке, соответствующей концу волнового вектора. Направление волнового вектора
соответствует направлению фазовой скорости, направление лучевого вектора -
групповой скорости волны. Вектор фазовой скорости задает направление переноса
фазы волны, вектор групповой скорости - направление переноса энергии. Для
прямых волн проекция вектора лучевой скорости на направление вектора фазовой
скорости (или вектора
векторы для различных участков этих кривых.
Волновые векторы начинаются в начале координат и заканчиваются на изочастотной
кривой. Каждый лучевой вектор перпендикулярен касательной к изочастотной кривой
в точке, соответствующей концу волнового вектора. Направление волнового вектора
соответствует направлению фазовой скорости, направление лучевого вектора -
групповой скорости волны. Вектор фазовой скорости задает направление переноса
фазы волны, вектор групповой скорости - направление переноса энергии. Для
прямых волн проекция вектора лучевой скорости на направление вектора фазовой
скорости (или вектора![]() на вектор
на вектор ![]() )
положительна, для обратных волн та же проекция отрицательна. Таким образом,
векторы
)
положительна, для обратных волн та же проекция отрицательна. Таким образом,
векторы ![]() ,
, ![]() и
и ![]() ,
, ![]() соответствуют прямым волнам, а векторы
соответствуют прямым волнам, а векторы ![]() ,
, ![]() и
и ![]() ,
, ![]() - обратным. Для наглядности, на
рис.7
участки изочастотных кривых, соответствующие прямым волнам, показаны тонкими
линиями, а соответствующие обратным - утолщенными. Выделенные точки на кривых
соответствуют границе между участками прямых и обратных волн. Эти точки, где
векторы фазовой и групповой скоростей взаимно перпендикулярны, получены, как
точки касания изочастотных кривых с прямыми, проведенными из начала координат.
Поскольку в этих точках направления векторов фазовой и групповой скоростей
взаимно перпендикулярны, то перенос энергии волной отсутствует.
- обратным. Для наглядности, на
рис.7
участки изочастотных кривых, соответствующие прямым волнам, показаны тонкими
линиями, а соответствующие обратным - утолщенными. Выделенные точки на кривых
соответствуют границе между участками прямых и обратных волн. Эти точки, где
векторы фазовой и групповой скоростей взаимно перпендикулярны, получены, как
точки касания изочастотных кривых с прямыми, проведенными из начала координат.
Поскольку в этих точках направления векторов фазовой и групповой скоростей
взаимно перпендикулярны, то перенос энергии волной отсутствует.
Рис.7. Изочастотные кривые для прямых и обратных волн
при ![]() = 1.05.
= 1.05.
9. ЭВОЛЮЦИЯ ИЗОЧАСТОТНЫХ КРИВЫХ ПРИ ИЗМЕНЕНИИ ЧАСТОТЫ.
Рассмотрим теперь эволюцию изочастотных кривых при изменении частоты волны.
Общий характер изменения изочастотных кривых довольно сложен, однако, резкой их
деформации можно ожидать лишь на частотах, где компоненты тензоров
проницаемостей ![]() ,
,
![]() ,
, ![]() ,
, ![]() , а также величины
, а также величины ![]() и
и ![]() расходятся или проходят через
нуль. Такими частотами являются следующие:
расходятся или проходят через
нуль. Такими частотами являются следующие:
1)
![]() =
= ![]() = 0,90 - магнитный
резонанс;
= 0,90 - магнитный
резонанс;
2)
![]() =
= ![]() = 1,00 - электрический
резонанс;
= 1,00 - электрический
резонанс;
3)
![]() = 1,0173 -
изменение знака
= 1,0173 -
изменение знака ![]() ;
;
4)
![]() = 1,1180 -
изменение знака
= 1,1180 -
изменение знака ![]() ;
;
5)
![]() = 1,1500 -
изменение знака
= 1,1500 -
изменение знака ![]() и
и
![]() .
.
Между этими частотами изочастотные кривые меняются сравнительно плавно, поэтому для рассмотрения эволюции изочастотных кривых при изменении частоты достаточно задать сетку частот, узлы которой лежат между перечисленными значениями.
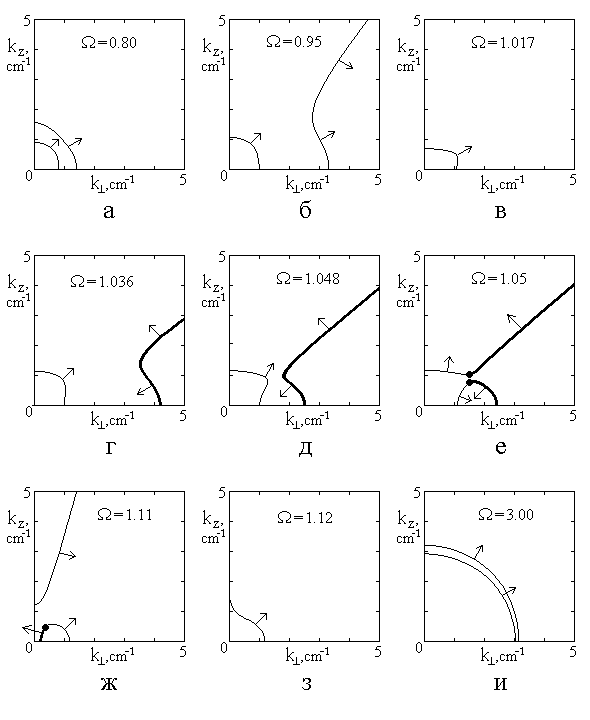
Пример таких изочастотных кривых приведен на рис.8. Здесь а соответствует ![]() = 0,80; б - 0,95; в -
1,017; г - 1,036; д - 1,048; е - 1,05; ж - 1,11; з - 1,12; и - 3,00 (последняя
кривая добавлена для полноты картины). Участки изочастотных кривых,
соответствующие обратным волнам, показаны утолщенными линиями. Стрелками
показаны направления векторов групповой скорости волн. Из рисунка видно, что в
большинстве случаев, кроме “в” и “з” изочастотные кривые имеют две ветви, а в
случаях “в” и “з” - одну. В случаях “г”, “д”,“е” и “ж” на одной из ветвей
имеется участок обратных волн, во всех остальных случаях волны - прямые.
Наиболее резкое изменение характера изочастотных кривых происходит в следующих
случаях:
= 0,80; б - 0,95; в -
1,017; г - 1,036; д - 1,048; е - 1,05; ж - 1,11; з - 1,12; и - 3,00 (последняя
кривая добавлена для полноты картины). Участки изочастотных кривых,
соответствующие обратным волнам, показаны утолщенными линиями. Стрелками
показаны направления векторов групповой скорости волн. Из рисунка видно, что в
большинстве случаев, кроме “в” и “з” изочастотные кривые имеют две ветви, а в
случаях “в” и “з” - одну. В случаях “г”, “д”,“е” и “ж” на одной из ветвей
имеется участок обратных волн, во всех остальных случаях волны - прямые.
Наиболее резкое изменение характера изочастотных кривых происходит в следующих
случаях:
1) от кривых “а” к кривым “б” - вблизи частоты магнитного резонанса 0,90 - когда верхняя (по рисунку) ветвь резко “перехлестывается” слева направо;
2) от кривых “в” к кривым “г” - вблизи частоты изменения знака ![]() - 1,0173, когда в
правом верхнем углу появляется дополнительная ветвь обратных волн;
- 1,0173, когда в
правом верхнем углу появляется дополнительная ветвь обратных волн;
3) от кривых “д” к кривым “е”, несколько выше частоты изменения знака ![]() - 1,0173, когда после
взаимного сближения левой и правой ветвей они соприкасаются, в результате чего
в их общей точке появляется разрыв, после чего новые кривые раздвигаются вверх
и вниз;
- 1,0173, когда после
взаимного сближения левой и правой ветвей они соприкасаются, в результате чего
в их общей точке появляется разрыв, после чего новые кривые раздвигаются вверх
и вниз;
Рис.8. Эволюция изочастотных кривых при изменении частоты.
4) от кривых “ж” к кривым “з” - вблизи частоты изменения знака ![]() - 1,1180, когда верхняя
ветвь уходит на бесконечность, а нижняя вблизи начала координат образует
сектор, протяженный по обеим осям;
- 1,1180, когда верхняя
ветвь уходит на бесконечность, а нижняя вблизи начала координат образует
сектор, протяженный по обеим осям;
5) от кривых “з” к кривым “и” - при переходе через частоту изменения знака ![]() и
и ![]() - 1,15, когда в начале координат
появляется новая ветвь, после чего обе ветви принимают форму, близкую к
четверти эллипса и при дальнейшем увеличении частоты удаляются от начала
координат.
- 1,15, когда в начале координат
появляется новая ветвь, после чего обе ветви принимают форму, близкую к
четверти эллипса и при дальнейшем увеличении частоты удаляются от начала
координат.
Перечисленными особенностями не исчерпывается все многообразие частотной
эволюции изочастотных кривых, однако, по-видимому, они являются наиболее
характерными. Полное исследование должно включать в себя рассмотрение
произвольного взаимного расположения частот магнитного и электрического
резонансов, а также произвольных значений коэффициентов заполнения пространства
магнитными сферами ![]() и
диполями
и
диполями ![]() .
Учет затухания внесет дополнительное разнообразие в рассматриваемые явления.
.
Учет затухания внесет дополнительное разнообразие в рассматриваемые явления.
Работа поддержана РФФИ, грант 01-02-16596-а.
[1] Адам Дж.Д. // ТИИЭР. 1988, т.76. №2. С.73-86.
[2] Исхак В.С. // ТИИЭР. 1988. Т.76. № 2. С. 86-104.
[3] Гуревич А.Г., Мелков Г.А. Магнитные колебания и волны. М.: Наука, 1994. 464 с.
[4] Веселаго В.Г. // УФН. 1967. Т.92. №.3. С. 517-526.
[5] I.V.Lindell, S.A.Tretyakov, K.I.Nikoskinen, S.Ilvonen. // Mikr.Opt.Tech.Lett. 2000. V.84. №18. P.4184-4187.
[6] Зубков В.И., Щеглов В.И. // Радиотехника и электроника. 1997. Т.42. № 9. С. 1114-1120.
[7] Зубков В.И., Щеглов В.И. // Письма в ЖТФ. 1998. Т.24. №13. С.1-7.
[8] Зубков В.И., Щеглов В.И. // ЖТФ. 1999. Т.69. № 2. С.70-77.
[9] Зубков В.И., Щеглов В.И. // Письма в ЖТФ. 1999. Т.25. №23. С.61-66.
[10] Зубков В.И., Щеглов В.И. // Радиотехника и электроника. 2000. Т.45. № 1. С.116-124.
[11] Pendry J.B., Holden A.J., Stewart W.J., Youngs I. // Phys.Rev.Lett. 1996. V.76. №25. P.4773-4776.
[12] Smith D.R., Padilla W.J., Vier D.C., Nemat-Nasser S.C., Schultz S. // Phys.Rev.Lett. 2000. V.84. №18. P.4184-4187.
[13] Вашковский А.В., Локк Э.Г. // Сб. трудов XVIII международной школы-семинара “Новые магнитные материалы микроэлектроники”, Москва, 2002, с.781-783.
[14] Щеглов В.И. // Сб. тезисов докладов Байкальской международно-практической конференции “Магнитные материалы”, Иркутск, 2001, с.38.
[15] Щеглов В.И. // Сб. трудов “Х Международной конференции по спинволновой электронике и гиромагнитной электродинамике”, Москва, 2001, с.157-166.
[16] Щеглов В.И. // Электронный “Журнал радиоэлектроники”, 2001, №8, http://jre.cplire.ru.
[17] Вашковский А.В., Стальмахов В.С., Шараевский Ю.П. Магнитостатические волны в электронике сверхвысоких частот. // Саратов, Изд.Саратовского университета, 1993, 320 с.
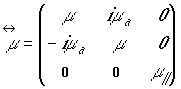 ,
(1)
,
(1)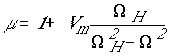 ,
, 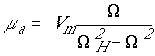 ,
, 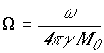 ,
, 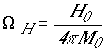 ,
(3)
,
(3)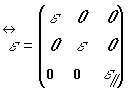 ,
(4)
,
(4)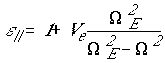 ,
(5)
,
(5)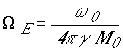 ,
, 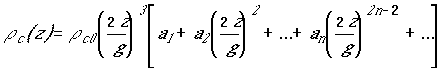 , (7)
, (7)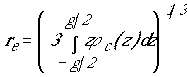 . (8)
. (8)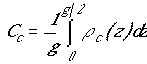 .
(9)
.
(9)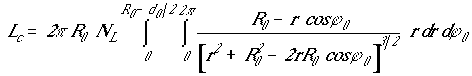 .(10)
.(10)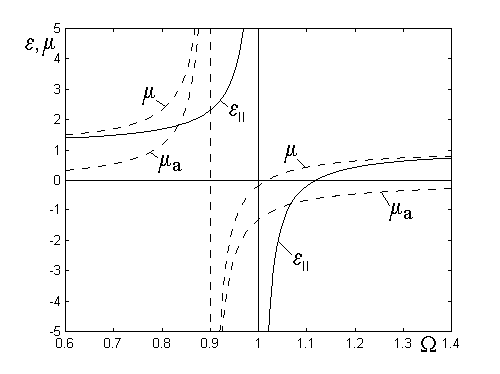
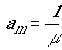
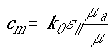 , (12)
, (12)