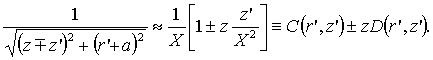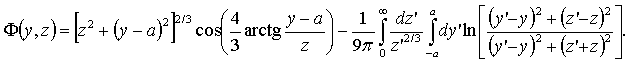|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 3, 2006 |
|
НОВЫЙ ПОДХОД ДЛЯ РАСЧЕТА ЭЛЕКТРОДОВ, ФОРМИРУЮЩИХ МОЩНЫЙ ЦИЛИНДРИЧЕСКИЙ ПУЧОК
Получена 1 августа 2006 г.
Рассматривается задача расчета электродов, формирующих осесимметричный пучок в режиме ограничения тока пространственным зарядом. При определении полного поля проводится систематический учет распределения поля пространственного заряда пучка. Приводится аналитическое выражение поля системы электродов в пространстве. Обсуждается ход нулевой эквипотенциали.
1. Введение
Проблема расчета осесимметричной системы электродов, формирующей цилиндрический пучок в режиме ограничения тока пространственным зарядом, принадлежит к классу задач, допускающих точное аналитическое решение, и поэтому носит методологический характер. Общепринятым является метод, предложенный в [1], когда осуществляется вырезка цилиндрической части потока Чайльда–Ленгмюра, а конфигурация электродов, обеспечивающих формирование такого пучка, определяется из решения задачи Коши уравнения Лапласа. Однако в такой постановке игнорируется то обстоятельство, что потенциал является суперпозицией потенциалов электродов и пространственного заряда пучка. Поэтому перед расчетом формы электродов следует уточнить распределение потенциала. Для этого к распределению поля Чайльда–Ленгмюра следует добавить поле пучка. Ясно, что это особенно важно вблизи катода, где плотность заряда пучка достигает больших значений (в гидродинамическом приближении стремится к бесконечности).
В настоящей работе представлено аналитическое решение рассматриваемой задачи формирования цилиндрического пучка с учетом распределения поля пространственного заряда пучка. Получены относительно простые выражения для расчета эквипотенциалей (т.е. формы электродов) в различных частях пространства. Исследован ход нулевой эквипотенциали вблизи катода.
2. Внешнее поле для формирования цилиндрического пучка
Поток Чайльда–Ленгмюра характеризуется следующими зависимостями потенциала
и плотности
от продольной координаты
Для расчета конфигурации электродов, формирующих осесимметричный пучок диаметром
, поступают следующим образом. Из потока Чайльда–Ленгмюра удаляют пространственный заряд, внешний по отношению к выделенному пучку, а произошедшие вследствие этого изменения поля компенсируют электродами. Форма и потенциалы последних подбираются такими, чтобы поле внутри пучка не изменилось.
Традиционно данная проблема сводится к следующей задаче [2]:
где
— оператор Лапласа,
— радиус пучка.
Ее решение получено, например, в [3] и имеет вид
Эквипотенциали в распределении
определяют конфигурацию и потенциал электродов, формирующих цилиндрический пучок.
Данный подход представляется обоснованным, если электроды полностью или частично погружены в пучок или, хотя бы, подходят вплотную к его границе. То есть, когда можно утверждать, что потенциальное распределение, в основном, задается непосредственно электродами.
Однако в ряде случаев (например, электронная пушка, генерирующая мощный пучок) электроды должны иметь отверстия, существенно превышающие поперечные размеры пучка. В формировании потенциала заметную роль начинает играть пространственный заряд самого пучка. Тогда потенциал
в задаче (2) оказывается суперпозицией потенциала формирующих электродов
и пространственного заряда
:
Действительно, по построению
при
, что и обеспечивает соответствующие граничные условия при
;
при
.
Поле пространственного заряда, распределенного по закону (1), с учетом его "отражения" в плоском катоде имеет вид
где
— полный эллиптический интеграл первого рода,
Таким образом, поле для формирования цилиндрического пучка может быть рассчитано по формуле
где
имеет вид (3), а
находится из (4).
3 Конфигурация электродов
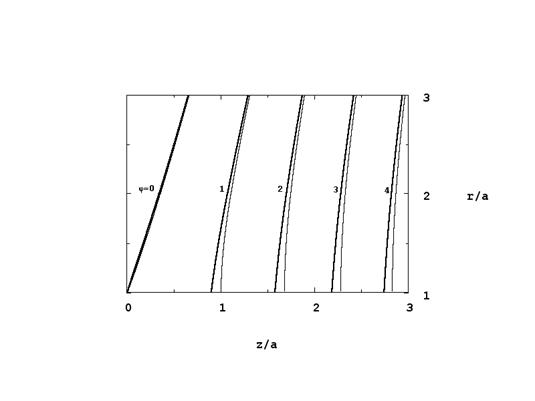
Форма электродов и их потенциалы могут быть определены как эквипотенциали распределения (6). На рис. 1 приведены эквипотенциали решений (3) и (6). Из их сравнения следует, что различие в распределениях потенциалов при
ничтожно, так как здесь влияние пространственного заряда незначительно. Поэтому новый подход на больших расстояниях от катода дает те же конфигурации электродов, что традиционный.
Чем ближе к катоду, тем различия значительнее. В этой связи более внимательно рассмотрим нулевую эквипотенциаль, играющую большую роль в формировании пучка. Найдем угол, под которым она выходит с катода. Для этого воспользуемся двумя обстоятельствами.
Во-первых, в малой окрестности края катода (
) задачу можно рассматривать как плоскую. Во-вторых, если в декартовой системе координат (
) потенциал плоскости
меняется вдоль
по закону
(потенциал вдоль
не меняется), то нулевая эквипотенциаль имеет вид
В частности,
при
.
Рассмотрим закон изменения
в (6) при
и
.
Из условия получения решения (2) имеем
при
. Исследуем поведение
. Вводя обозначение
, можно представить выражение (5) в виде
Воспользовавшись разложением
, справедливым при
, получим
Аналогичным образом имеем
Подставляя полученные соотношения в (4), получим
т.е. поле пропорционально первой степени
. Так как
при малых
, то из (7) получаем, что искомый угол равен
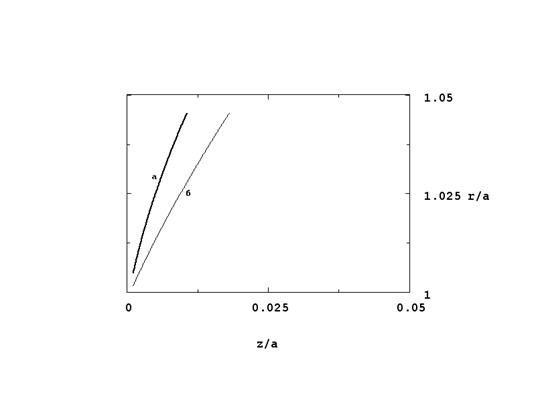
. Иными словами, нулевая эквипотенциаль спрягается с катодом гладким образом, без образования углов. Это является принципиальным отличием от традиционного решения, утверждающего, что эквипотенциаль составляет с нормалью к поверхности катода угол
. Подробнее форма нулевой эквипотенциали приведена на рис. 2. Здесь же дана нулевая эквипотенциаль, полученная из (3).
Проведем более детальное сравнение формы эквипотенциалей, получающихся при классическом и новом подходах. Новые эквипотенциали располагаются ближе к катоду. Учет пространственного заряда приводит к тому, что границе пучка перпендикулярна лишь нулевая эквипотенциаль, а остальные подходят к ней под углом, что существенным образом отличается от хода эквипотенциалей, полученных при пренебрежении пространственным зарядом. В последнем случае, как показано в [3], наоборот, все эквипотенциали, кроме нулевой, перпендикулярны границе пучка, а нулевая подходит под углом
.
Полученные результаты позволяют утверждать, что традиционное и уточненное решения различаются вблизи катода. При этом разность является важной скорее в методологическом плане, чем в практическом. Тем не менее, в ряде задач, например, при создании электронных пушек для формирования пучков с малым фазовым объемом (эмиттансом), необходимо точное соблюдение конфигураций и потенциалов электродов для минимизации аберраций. И тогда применение уточнения дает возможность решить поставленную задачу. Следует также отметить, что различия двух решений могут быть иными в случае пучков других конфигураций (например, сходящихся).
Аналогично, для формирования планарного пучка (
), полученного из потока Чайльда-Ленгмюра (1), необходимо электродами создать следующее распределение поля вне пучка (воспользовавшись симметрией системы относительно плоскости
, приведем выражение лишь для
)
Список литературы
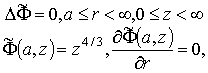 (2)
(2) (3)
(3)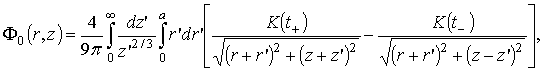 (4)
(4)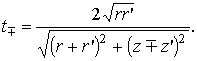 (5)
(5)