|
“ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ” N 8, 2009 |
УДК 517: 519.6: 535+537.8: 621.37
РАЗРАБОТКА И ИССЛЕДОВАНИЕ КОМПЛЕКСА ПРОГРАММ ДЛЯ РАСЧЕТА ОСНОВНЫХ ХАРАКТЕРИСТИК ИНТЕГРАЛЬНО-ОПТИЧЕСКИХ ВОЛНОВОДОВ В СИСТЕМЕ ВИЗУАЛЬНОГО ПРОГРАММИРОВАНИЯ DELPHI И С++
А.А. Егоров,1 А.В.Ставцев2
1 Институт общей физики им. А.М. Прохорова РАН,2 РУДН, НИЛ ВФиММ, сектор теоретической и прикладной оптики
Получена 18 августа 2009 г.
Дано описание разработанных авторами базовых вариантов программ на языках Паскаль в системы визуального программирования Delphi и С++ в системе визуального программирования C++ Builder, позволяющих рассчитывать дисперсионные зависимости и поля для различных ТЕ и ТМ мод симметричных и несимметричных интегрально-оптических волноводов.
Использование средств визуального программирования, по нашему убеждению, является наиболее удобным инструментом для построения и анализа математических моделей подобных сложных явлений и объектов.
PACS: 02.30.Uu, 02.30.Zz, 02.50.Ey, 03.65.Db, 03.65.Nk, 42.25.Fx, 42.82.-m
Ключевые слова: интегральная оптика, лазерное излучение, моды волновода, дисперсионное соотношение, проблема волноводного рассеяния, волноводные нерегулярности, интегрально-оптический датчик, численное моделирование, визуальное программирование
1. Введение
Совершенствование и активное развитие теоретических и компьютерных методов исследования и быстрый технологический прогресс стимулировали интерес к разработке векторной теории распространения, а также рассеяния электромагнитного излучения в различных нерегулярных волноводах [1-21].
Решение трехмерной электродинамической задачи имеет одно из ключевых значений для развития нанотехнологий в интегральной оптике и волноводной оптоэлектронике. Трехмерное решение электродинамической задачи рассеяния позволяет, например, точнее учесть влияние нерегулярностей структуры на характеристики оптических интегральных схем [17, 21]. В последние годы активно разрабатываются различные типы интегрально-оптических химических сенсоров, что обусловлено рядом их преимуществ: высокой чувствительностью, быстрым срабатыванием, простотой мультиплексирования сигнала и применением интегральных технологий [22-24]. Важно отметить, что рассеяние лазерного излучения в волноводе [1-21] является одним из важнейших лимитирующих факторов достижения предельной чувствительности интегрально-оптических сенсоров [22-24]. При этом существует очевидный интерес к разработке и исследованию интегрально-оптических сенсоров именно на вытекающих модах и модах излучения, поскольку появляется возможность повышения чувствительности соответствующих интегрально-оптических сенсоров. С этой точки зрения исследование различных явлений в нерегулярных интегрально-оптических волноводах, поддерживающих вытекающие моды и моды излучения, является актуальной задачей.
Если пренебречь рассмотрением возникающих при рассеянии поляризационных эффектов, то можно упростить трехмерное векторное уравнение. Тогда рассматриваемое двухмерное решение исходной задачи ищется в виде суперпозиции ортогональных ТЕ и ТМ-мод идеального прямолинейного волновода. Решение прямой задачи волноводного рассеяния может быть получено в общем случае в виде амплитудно-фазового распределения в некоторой зоне излучения. Может быть также получено решение в виде распределения (диаграммы рассеяния) интенсивности излучения рассеянного на нерегулярностях структуры волновода, например, в ближней или дальней зонах излучения.
В данной работе авторы рассмотрели для примера некоторые возможности системы визуального программирования Delphi и С++ в системе визуального программирования C++ Builder для исследования математических моделей явления волноводного распространения и излучения электромагнитных волн в трехслойных интегрально-оптических волноводах, поддерживающих моды излучения подложки.
2. Основные соотношения и метод исследования
Уравнения Максвелла для электромагнитного поля в случае не поглощающей неоднородной линейной изотропной среды (в отсутствие токов и зарядов) в системе СИ сводятся к уравнениям:
,
, (1)
где
– диэлектрическая проницаемость среды;
– магнитная проницаемость среды;
,
– относительные диэлектрическая и магнитная проницаемости соответственно (в немагнитной среде полагается
= 1);
и
– это электрическая и магнитная постоянные соответственно;
=
,
– показатель преломления среды (здесь и далее – слоя рассматриваемой многослойной интегрально-оптической структуры),
,
,
– частота электромагнитного поля;
,
– вектора напряженностей электрического и магнитного полей.
При записи уравнений (1) учтено, что для линейной изотропной среды справедливы следующие соотношения:
,
, где
– вектор электрической индукции,
– вектор магнитной индукции.
Из уравнений (1) можно получить уравнение, описывающее поле
в оптическом волноводе с произвольными трехмерными нерегулярностями, которое в декартовых координатах имеет следующий вид:
, (2)
где
для случая, когда скалярные составляющие векторов напряженностей электрического и магнитного (E и H) полей отнесены к фиксированным декартовым составляющим системы координат.
Рассматривается случай распространения в нерегулярном волноводе вдоль оси
первой четной (фундаментальной) ТЕ0-моды с компонентами
,
,
; в дальнейшем индекс «0» у компонент поля направляемой моды опустим. Распространение других типов мод исследуется аналогично.
При наличии малых по величине нерегулярностей направляемые моды испытывают возмущение в области нерегулярности, и небольшая часть мощности направляемых мод может излучиться (3D-scattering) как в другие типы волноводных мод (межмодовое преобразование), так и в окружающее пространство (in-plane и out-of-plane scattering).
Приближенное решение уравнения (2) может быть получено, например, в первом приближении теории возмущений методом функций Грина в виде свертки некоторой трехмерной функции Грина с выражением для источника [16, 17]. При таком подходе в волноводе могут возникать гибридные моды, имеющие шесть компонент поля, а не три, как ТЕ- и ТМ-моды. Для гибридных мод не выполняется условие
= 0, т.е. существуют вариации полей в этом направлении. Таким образом, в случае трехмерных нерегулярностей любое произвольное распределение поля планарного интегрально-оптического волновода необходимо представлять в виде разложения по всем возможным модам плоского волновода, включая суммирование и интегрирование по модам, соответствующим вариации поля по второй поперечной координате – по оси
. Для более подробного знакомства с проблемами, возникающими при трехмерном векторном рассмотрении исходной электродинамической задачи, рекомендуем посмотреть работы [1-3, 16, 17] и цитированную там литературу.
Если пренебречь рассмотрением возникающих при рассеянии поляризационных эффектов, то можно упростить трехмерное векторное уравнение (2). Для этого надо потребовать, чтобы относительное изменение диэлектрической проницаемости на расстоянии одной длины волны было много меньше единицы. Это условие часто выполняется в оптических средах. В этом случае деполяризационный член
в уравнении много меньше двух других (его отношение к любому из них по порядку величины равно примерно
, где
– величина отклонения относительной диэлектрической проницаемости от среднего значения
). Следовательно, при
<< 1 точное трехмерное векторное уравнение (2) можно заменить приближенным волновым векторным уравнением:
, (3)
которое справедливо для каждой декартовой компоненты вектора электрического поля. Для основной ТЕ-моды, распространяющейся вдоль оси
, при условии
= 0, векторное волновое уравнение (3) принимает хорошо известный скалярный вид:
, (4)
где
,
– описывает регулярные свойства соответствующей среды волновода (принимает значения
,
или
соответственно, 1 – покровный слой, 2 – волноводный слой, 3 – подложка), а добавка
описывает нерегулярности структуры волновода (как неровности границ раздела сред волновода, так и неоднородности показателя преломления в каждом m-м слое волновода). Для применения при исследовании, например, теории возмущений
не обязательно должна быть величиной малого порядка. Достаточно, чтобы область, в пределах которой эта добавка отличается от нуля, была достаточно узкой.
Если условие
выполняется, т.е. рассматривается двухмерное решение исходной задачи (2D-scattering), можно записать любое произвольное распределение поля планарного волновода в виде суперпозиции ортогональных ТЕ и ТМ-мод идеального прямолинейного волновода.
Итак, любое произвольное распределение поля, например,
для ТЕ0-моды, планарного интегрально-оптического волновода представим в виде разложения (в ряд и интеграл) по ортогональному набору (базисных) функций [1-3]:
, (5)
где, первая сумма описывает все четные и нечетные ТЕ-моды, а комбинация из суммы (в общем случае – по четным и нечетным модам излучения) и интеграла – все моды излучения. В выражении (5):
, т.е. переменная
принадлежит множеству натуральных чисел I: изменяется от 0 до +∞;
– коэффициенты разложения направляемых мод
;
– эффективная амплитуда рассеяния ТЕ-мод, определяемая как коэффициент разложения поля по всем модам излучения
;
и
– поперечная и продольная составляющие постоянных распространения мод излучения (вдоль осей
и
соответственно),
,
– показатель преломления соответствующего слоя многослойного интегрально-оптического волновода.
В данном случае для анализа распространения направляемых мод вдоль оси
и их рассеяния используется полная ортогональная система направляемых мод и мод излучения регулярного волновода, что приводит к уравнениям связанных мод [1-3]. Вопрос рассмотрения вытекающих мод, у которых постоянная распространения
является в общем случае комплексной, а толщина волноводного слоя – меньше критической – выходит за рамки рассмотрения данной работы. В этом случае неприменим метод разложения по полной системе направляемых мод и мод излучения регулярного планарного волновода [1-3], поскольку вытекающие моды не являются ортогональными [3].
Аналогично (5)имеем для ТМ-мод:
, (6)
Коэффициенты разложения
,
,
и
в выражениях (5), (6) находятся с помощью соотношений ортогональности [1-3].
Затем может быть найдена, например, полная переносимая в волноводе мощность лазерного излучения или, например, мощность излучения, обусловленная рассеянием направляемой моды на нерегулярностях волновода. Если рассеяние происходит на случайных нерегулярностях, то для нахождения мощности рассеянного излучения может применяться усреднение по эргодическому ансамблю.
Итак, решение прямой задачи волноводного рассеяния может быть получено в виде амплитудно-фазового распределения или в виде решения, описывающего распределение интенсивности лазерного излучения рассеянного на нерегулярностях структуры волновода.
При экспериментальных исследованиях применимость двухмерного анализа задачи рассеяния может быть обеспечена, например, установкой в дальней зоне (или в эквивалентной ей плоскости Фурье) щелевой диафрагмы, расположенной параллельно плоскости падения и поляризатора.
Измеренная таким образом двухмерная диаграмма рассеяния может быть использована для нахождения приближенного корректного решения обратной задачи рассеяния на трехмерных нерегулярностях структуры интегрально-оптического волновода.
Если нельзя использовать двухмерное рассмотрение, то решается векторная трехмерная электродинамическая задача о распространении и рассеянии направляемой фундаментальной волноводной моды в интегрально-оптическом волноводе. При этом могут быть использованы, например, такие хорошо известные методы, как метод связанных мод, метод теории возмущений и метод функций Грина [1-3].
На следующем этапе решения поставленной проблемы самым важным является поиск метода численного исследования полученной системы уравнений. Решение последней проблемы зачастую определяется наличием у исследователей соответствующих программных средств и компьютера, обладающего необходимой производительностью и оперативной памятью.
С целью выбора оптимальных путей решения последней задачи, авторы сравнили возможности нескольких популярных математических пакетов и языков программирования (по ряду важных критериев):
§ удобство использования;
§ скорость вычисления математических операций;
§ потенциальное время, которое потребуется на решение задачи;
§ возможность использовать полученные результаты в дальнейшем;
§ возможность расширения базового набора функций;
§ возможность получить качественное представление результатов.
В результате сравнения были выявлено следующее. Математические пакеты предоставляют пользователю широкий набор готовых для выполнения наиболее распространенных, но при этом сложных операций (таких как вычисление коэффициентов рядов, разложение на множители, матричные и векторные операции и т.п.), позволяя при этом получать качественное представление результатов в виде всевозможных графиков, вид и способ отображения может быть легко настроен. Однако из-за того, что разные виды математических пакетов могут решать лишь ограниченный круг задач, нельзя выбрать какой-то один оптимальный пакет, который позволил бы нам реализовать в нем полностью все наши потребности. Базовый набор функций математических пакетов ограничен набором наиболее стандартных численных методов, однако в ряде случаев они могут оказаться малоэффективными. Если для решения задачи потребуется добавить какой-то нестандартный метод, то его реализация может оказаться сложнее, чем в обычном языке программирования.
Алгоритмические языки программирования предоставляют исследователю больше возможней, чем математические пакеты:
· алгоритмические языки не имеют ограничений присутствующих в математических пакетах;
· разработчик не привязан к каким-то конкретным функциям или способам представления результатов, при этом все стандартные математические алгоритмы, которые есть в математических пакетах, также реализованы и доступны для большинства языков программирования в виде внешних математических библиотеках;
· любой алгоритм можно изменить для решения конкретной задачи;
· скорость работы математических алгоритмов выше, чем в математических пакетах;
· доступно множество всевозможных внешних модулей, значительно расширяющие возможности языка.
Любой язык программирования предоставляет разработчику лишь набор простейших базовых функций, из которых затем можно построить достаточно сложный алгоритм. Из доступных компилируемых языков программирования под Windows авторы выбрали язык Паскаль в системе визуального программирования Delphi [24]. По сравнению с другими языками Delphi обладает следующими достоинствами:
· доступно множество дополнительных компонент, позволяющих строить графики и поверхности;
· доступно множество математических библиотек и реализаций численных методов;
· в отличие от С/С++, проверяет границы значений массивов (в расчеты не попадают данные из не инициализированных областей памяти);
· удобная среда разработки и отладки;
· доступна обширная русскоязычная документация по языку.
С целью проверки эффективности работы в данной среде было написано программное средство для расчета дисперсионных зависимостей ТЕ и ТМ мод для ряда практически важных оптических волноводов. Для оценки эффективности был сделан также вариант программы в языке С++ визуального программирования C++ Builder.
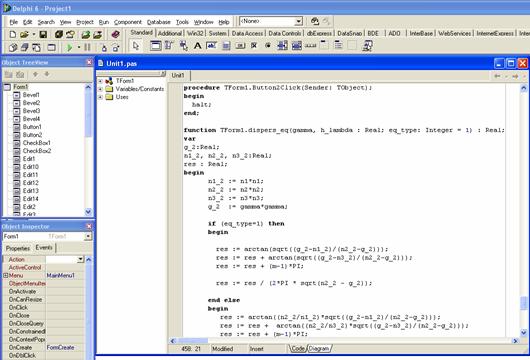
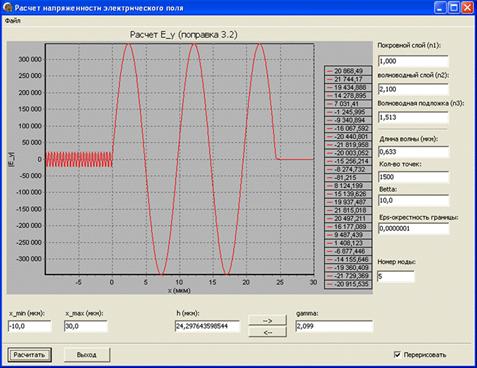
Интерфейс написанной программы представлен на рис. 1 (вид интерфейса программы написанной в С++ Builder аналогичен изображенному на рис. 1).
Рис. 1. Фрагмент интерфейс программы в системе визуального программирования Delphi.
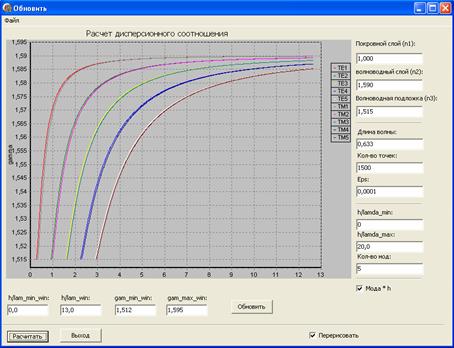
На рис. 2 – рис. 3 представлены построенные в соответствии с этой программой дисперсионные зависимости
для первых пяти ТЕ и ТМ мод двух типичных регулярных трехслойных планарных интегрально-оптических волноводов (см. рис. 3): полистиролового и танталового (Ta2O5). Справа на рис. 2, 3 представлена легенда с краткими пояснениями.
Для расчетов использовалось хорошо известное представление дисперсионного соотношения в тригонометрическом виде:
, (7)
где
– постоянная распространения направляемой ТЕ-моды вдоль оси
(см. рис. 4);
– толщина волноводного слоя;
– коэффициент фазового замедления (эквивалентный показатель преломления волновода, как среды в которой распространяется электромагнитная волна, показывает во сколько раз скорость распространения волны в вакууме больше скорости распространения волны в волноводе);
– вертикальная составляющая постоянной распространения направляемой ТЕ-моды при
(полагается, что нуль оси
находится на границе волноводный слой (пленка)-воздух);
– вертикальная составляющая постоянной распространения направляемой ТЕ-моды при
;
– целое число,
= 1, 2, … (при
= 1 из (1) получается дисперсионное соотношение для ТЕ0-моды (фундаментальной ТЕ-моды).
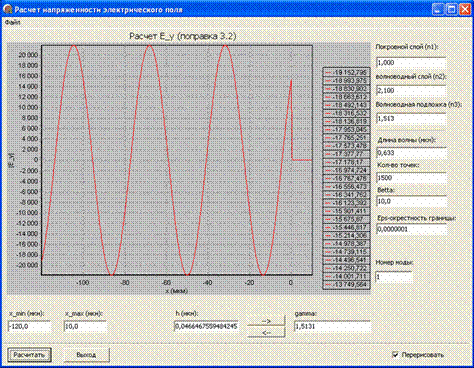
На рис. 5–7 изображены рассчитанные зависимости модуля (в произвольных единицах) напряженности поля излучательных ТЕ-мод подложки
в средах 1, 2, 3 для регулярного трехслойного планарного волновода при фиксированной толщине волноводного слоя.
Рис. 2. Дисперсионные зависимости
для первых пяти ТЕ и ТМ мод полистиролового волновода.
Рис. 3. Дисперсионные зависимости
для первых пяти ТЕ и ТМ мод танталового (Ta2O5) волновода.
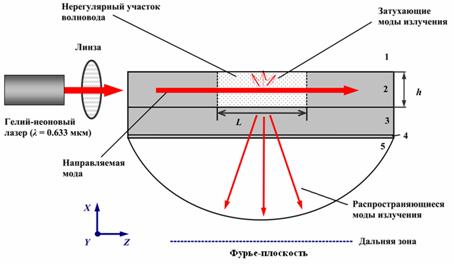
Рис. 4. Схема, иллюстрирующая рассеяние лазерного излучения в нерегулярном интегрально-оптическом волноводе: 1 – покровный слой (воздух), 2 – волноводный слой (пленка); 3 – подложка; 4 – иммерсия; 5 – кварцевая полусфера; L – длина нерегулярной области; h – толщина волновода.
Из рисунков видно, что характер распределения поля при заданном изменении
наиболее сильно изменяется в подложке, что и следовало ожидать, а также в пленке. А в воздухе – оно мало меняется. Это связано в основном с тем, что эти
близки к величине
и поле здесь сильнее проникает в подложку, чем при значениях
в середине диапазона его изменения: от
до
.
В целом же эти рисунки отражают хорошо известное парциальное распределение полей (и мощностей) в средах образующих интегрально-оптический волновод, у которого наблюдаются излучательные моды подложки. Исследованы также особенности распределения полей вдоль оси
для мод более высокого порядка: ТЕ5 (индекс мод отсчитывается от 1). На рисунках 6 и 11 приведены два из полученных графиков зависимостей
.
Поле излучательных ТЕ-мод подложки задавалось в следующем виде (см., например, [5, 6]):
=
(8)
где
,
– частота электромагнитного поля;
и
– это электрическая и магнитная постоянные;
– мощность, переносимая волной по волноводу в направлении оси
через единицу его ширины (по оси
), в расчетах брали
= 1 Вт/м. Остальные обозначения даны после выражения (7)
Для выполнения граничных условий [5]
, (9)
, (10)
необходимо выполнение следующих соотношений [5, 6]:
,
, (11)
где
и
– фазовые сдвиги, появляющиеся при полном внутреннем отражении на границах раздела пленка-подложка и пленка-воздух.
Важно отметить, что в данном случае отсутствует дисперсионное соотношение, которое приводит к дискретным значениям величины
, поэтому надо выбирать величину
в качестве независимой непрерывной переменной.
Справа на рис. 5 – рис. 11 представлена легенда с краткими пояснениями, где gamma – коэффициент фазового замедления
,
– толщина волновода,
– расстояние вдоль вертикальной оси, отсчитываемое от границы раздела пленка-подложка.
Группа настроек отображения (на рис. 5 – рис. 11 внизу), – задает координаты окна отображения графика поля излучательный моды подложки.
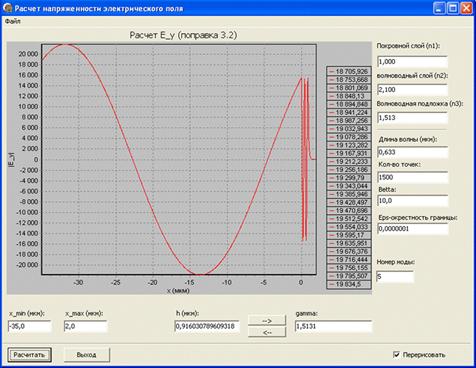
Рис. 5. Модуль нормированного значения поля излучательной ТЕ1-моды подложки для коэффициента фазового замедления
= 1.5131.
Рис. 6. Модуль нормированного значения поля излучательной ТЕ5-моды подложки для коэффициента фазового замедления
= 1.5131.
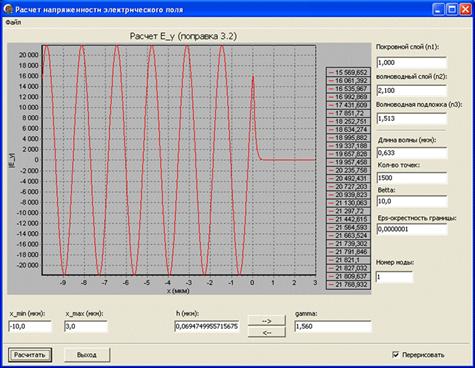
Рис. 7. Модуль нормированного значения поля излучательной ТЕ1-моды подложки для коэффициента фазового замедления
= 1,560.
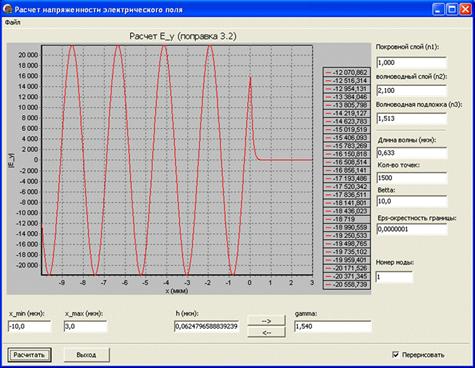
Рис. 8. Модуль нормированного значения поля излучательной ТЕ1-моды подложки для коэффициента фазового замедления
= 1,540.
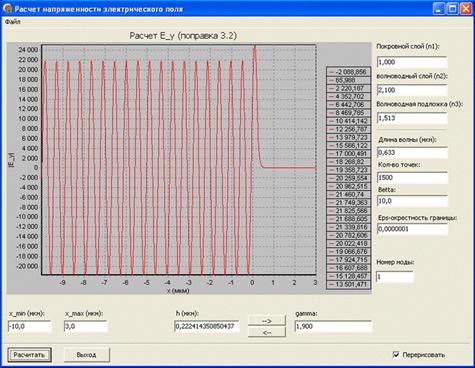
Рис. 9. Модуль нормированного значения поля излучательной ТЕ1-моды подложки для коэффициента фазового замедления
= 1,900.
Рис. 10. Модуль нормированного значения поля излучательной ТЕ1-моды подложки для коэффициента фазового замедления
= 2,099.
Рис. 11. Модуль нормированного значения поля излучательной ТЕ5-моды подложки для коэффициента фазового замедления
= 2,099.
В заключение отметим, что для случая распространения в волноводе ТМ-мод получены аналогичные зависимости.
Времена расчета всех кривых на компьютере типа Пентиум 4 с тактовой частотой 3.3 ГГц и оперативной памятью 1 Мб, для обеих программ примерно равны и составляют не более 10 с.
Литература
1. Маркузе Д. Оптические волноводы. – М.: Мир, 1974.
2. Содха М.С., Гхатак А.К. Неоднородные оптические волноводы. – М.: Связь, 1980.
3. Снайдер А., Лав Дж. Теория оптических волноводов. – М.: Радио и связь, 1987.
4. Дерюгин Л.Н., Марчук А.Н., Сотин В.Е. Излучение с плоского диэлектрического волновода // Изв. вузов. Радиоэлектроника. 1970. Т. 13. № 3. С. 309-315.
5. Suematsu Y., Furuya K. Propagation mode and scattering loss of a two dimensional dielectric waveguide with gradual distribution of refractive index // IEEE Trans. on MTT. 1972. V. 20. No. 7. P. 524-531.
6. Tsai T.L., Tuan H.S. Reflection and scattering by a single groove in integrated optics // IEEE J. of QE. 1974. V. 10. No. 3. P. 326-332.
7. Киселев В.А. О распространении, преобразовании и генерации поверхностных световых волн в тонких пленках с гармонически промодулированным показателем преломления // Квантовая Электроника. 1974. Т. 1. № 4. С. 899-907.
8. Прохоров А.М., Спихальский А.А., Сычугов В.А., Шипуло Г.П. Отражение и излучение Н- и Е-волн на гофрированном участке диффузионного волновода // Квантовая Электроника. 1976. Т. 3. № 9. С. 1941-1947.
9. Imai M., Miyanaga S., Asakura T. Mode conversion and radiation loss caused by refractive-index fluctuations in an asymmetric slab waveguide // IEEE J. of QE. 1977. V. 13. No. 4. P.255-262.
10. Андлер Г., Черемискин И.В. Рассеяние в диэлектрическом волноводе со случайными искажениями стенок // Изв. вузов. Радиоэлектроника. 1981. Т. ХХIV. № 9. С. 68-70.
11. Андлер Г., Егоров А.А., Черемискин И.В. Определение параметров шероховатости оптической поверхности по рассеянию в диэлектрическом волноводе // Оптика и Спектроскопия. 1984. Т. 56. № 4. С. 731-735.
12. Егоров А.А. Характеристики излучения, рассеянного на шероховатостях поверхности подложки планарного волновода // Поверхность. Физика, химия, механика. 1994. № 5. С. 72-76.
13. Egorov A.A. Theory of waveguide optical microscopy // Laser Physics. 1998. V. 8. No. 2. P. 536-540.
14. Yegorov A.A. A new algorithm of restoring the autocorrelation function of subwavelength statistic surface roughness by light scattering in integrated optical waveguide in the presence of a high additive stochastic noise // Proc. SPIE. 2002. V. 4900. P. 792-801.
15. Егоров А.А. Восстановление экспериментальной автокорреляционной функции и определение параметров статистической неровности поверхности по данным рассеяния лазерного излучения в интегрально-оптическом волноводе // Квантовая Электроника. 2003. Т. 33. № 4. С. 335-341.
16. Егоров А.А. Автореф. дисс. … д.ф.м.н. Теория и математическое моделирование рассеяния лазерного излучения в нерегулярном интегрально-оптическом волноводе при наличии шума. – М.: РУДН, 2005.
17. Егоров А.А. Теория волноводного рассеяния света в интегрально-оптическом волноводе при наличии шума // Изв. вузов. Радиофизика. 2005. Т. 48. № 1. С. 63-75.
18. Egorov A.A. Super resolution in the waveguide inverse light scattering problem // Journal of Radio Electronics. 2007. No. 6.
19. Егоров А.А. Обратная задача рассеяния монохроматического света в статистически нерегулярном волноводе: теория и численное моделирование // Оптика и Спектроскопия. 2007. Т. 103. № 4. C. 638-645.
20. Egorov A.A. Influence of light scattering by 3D-irregularities on the characteristics of the integrated optical devices using for optical signal processing // Journal of Radio Electronics. 2008. No. 2.
21. Egorov A.A., Egorov M.A., Chekhlova T.K., Timakin A.G. Low-loss inexpensive integrated-optical waveguides as a sensitive gas sensor // ICO Topical Meeting on Optoinformatics/Information Photonics 2008. September 15-18, 2008. St. Petersburg. Russia. St. Petersburg: ITMO. P. 208-211.
22. Егоров А.А., Егоров М.А., Чехлова Т.К., Тимакин А.Г. Применение интегрально-оптических датчиков для контроля опасных газообразных веществ // Датчики и Системы. 2008. № 1. С. 25-28.
23. Егоров А.А., Егоров М.А., Чехлова Т.К., Тимакин А.Г. Исследование компьютеризированного интегрально-оптического датчика концентрации газообразных веществ // Квантовая электроника. 2008 Т. 38. № 8. С. 787-790.
24. Гофман В.Э., Хомоненко А.Д. Delphi. Быстрый старт. – СПб.: БХВ-Петербург, 2003. – 288 с.