КОМПЛЕКСНАЯ ДИЭЛЕКТРИЧЕСКАЯ ПРОНИЦАЕМОСТЬ И АС-ПРОВОДИМОСТЬ МОНОКРИСТАЛЛОВ GaSe,
ВЫРАЩЕННЫХ ИЗ ГАЗОВОЙ ФАЗЫ
С. Н.
Мустафаева 1, М. М.
Асадов 2
1 Институт физики Национальной академии наук, Баку, Азербайджан
2 Институт химических проблем Национальной академии наук, Баку, Азербайджан
Получена 16 июля 2011 г.
Аннотация. В полученных слоистых монокристаллах GaSe изучена частотная дисперсия действительной (ε) и мнимой (ε″) составляющих комплексной диэлектрической проницаемости, тангенса угла диэлектрических потерь tgd (f) и ac-проводимости (σac) в области частот f = 5´104–3.5´107 Гц. Установлено, что в изученных кристаллах имеет место релаксационная дисперсия ε и ε″. Показано, что диэлектрические потери в GaSe обусловлены релаксационной поляризацией и сквозной проводимостью. В диапазоне частот f = 105–3.5´107 Гц ac-проводимость кристалла GaSe подчинялась закономерности σac ~ f 0.8, характерной для прыжкового механизма переноса заряда по локализованным вблизи уровня Ферми состояниям. Оценены плотность (NF) и разброс (∆E) этих состояний NF = 1.3´1018 эВ–1·cм–3, ∆E = 0.048 эВ, среднее время (τ) и расстояние (R) прыжков τ = 0.1 мкс и R = 197 Å, а также радиус локализации а = 32 Å.
Ключевые слова: диэлектрические свойства, частота, ac-проводимость, монокристалл GaSe.
Abstract. The frequency dispersion of the real (ε) and imaginary (ε ") components of the complex dielectric constant, dielectric loss tangent tan d (f) and ac-conductivity (σac) of the obtained layered GaSe single crystals have been studied in the frequency range f = 5 ´ 104-3.5 ´ 107 Hz. It was found that in the studied crystals a relaxation dispersion of ε and ε " takes place. It is shown that the dielectric losses in GaSe are caused by the relaxation polarization and pass-through conduction. In the frequency range f = 105-3.5 ´ 107 Hz ac-conductivity of the crystal GaSe varies as σac ~ f 0.8, typical for hopping charge transport mechanism between localized states near the Fermi level. The Fermi- level density of states NF = 1.3 ´ 1018 eV-1 ×cm-3 and the spread of these states ΔE = 0.048 eV, the average time τ = 0.1 ms and distance R = 197 Å of jumps, as well as the localization radius a = 32 Å have been estimated.
Keywords: dielectric properties, frequency, ac-conductivity, GaSe single crystal.
ВВЕДЕНИЕ
Монокристаллы GaSe принадлежат к классу слоистых полупроводников, характеризующихся анизотропными физическими свойствами. В [1,2] были изучены процессы переноса заряда в монокристаллах GaSe, выращенных методом Бриджмена. Было показано, что в них при низких температурах (Т < 200 К) на постоянном токе (dc) и при Т = 300 К на переменном токе (ac) имеет место прыжковый механизм переноса заряда по состояниям, локализованным вблизи уровня Ферми.
В настоящей работе представлены результаты измерений диэлектрических свойств и ас-проводимости монокристаллов р-GaSe, выращенных из газовой фазы.
МЕТОДИКА ЭКСПЕРИМЕНТА
Соединение GaSe синтезировано путем сплавления исходных компонентов высокой степени чистоты (³ 99.999%) в ваккумированной кварцевой ампуле. Монокристаллы GaSe были выращены из синтезированного соединения методом химических транспортных реакций в эвакуированной кварцевой ампуле с использованием йода в качестве носителя. Полученные монокристаллы GaSe представляли собой ярко-красные слои, обладающие высокой оптической прозрачностью.
Образцы из GaSe для электрических измерений были изготовлены в виде плоских конденсаторов. В качестве электродов использована серебряная паста. Толщина кристаллического образца из GaSe составляла 100мкм.
Диэлектрические коэффициенты монокристаллов GaSe измерены резонансным методом с помощью куметра TESLA BM 560. Диапазон частот переменного электрического поля составлял 5´104–3.5´107 Гц.
Все диэлектрические измерения проведены при 300 K. Воспроизводимость положения резонанса составляла по емкости ± 0.2 пФ, а по добротности (Q = 1/tgδ) ±1.0–1.5 деления шкалы. При этом наибольшие отклонения от средних значений составляли 3 – 4 % для ε и 7 % для tgδ.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
На рис. 1 приведены частотные зависимости диэлектрической проницаемости (ε) образца GaSe.
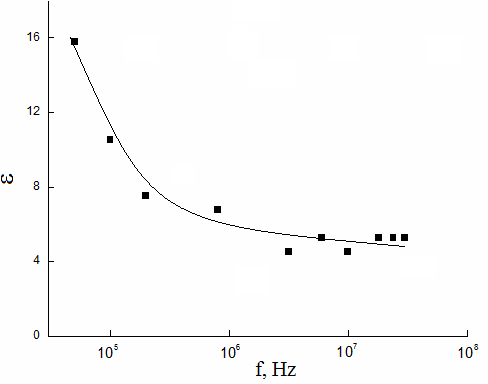
Рис. 1. Частотная дисперсия действительной составляющей комплексной диэлектрической проницаемости монокристалла GaSe.
Как видно из рис. 1, ε изученного образца претерпевает существенную дисперсию. По мере увеличения частоты от 5´104 до 3.5´107 Гц значение ε уменьшается ~ в 4 раза. Наблюдаемое в экспериментах монотонное уменьшение диэлектрической проницаемости GaSe свидетельствует о релаксационной дисперсии [3].
На рис.
2 показана частотная дисперсия коэффициента диэлектрических потерь ![]() в GaSe.
в GaSe.
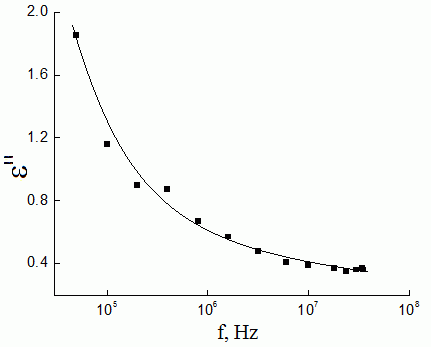
Рис. 2. Частотная зависимость мнимой составляющей комплексной диэлектрической проницаемости монокристалла GaSe.
Значение ε″ варьируется в пределах 1.85–0.36 во всей изученной области частот. Величина ε″ с ростом частоты вплоть до 3.5´107 Гц уменьшается примерно в 5 раз, т.е. дисперсионная кривая ε″(f) характеризуется довольно ощутимым спадом во всем изученном диапазоне частот.
На частотной зависимости тангенса угла диэлектрических потерь в кристалле GaSe при f = 1.6 ×106 Гц наблюдался максимум (рис. 3), а затем кривая tgd (f) носила спадающий характер. Форма экспериментальной кривой tgd (f) в GaSe характерна для частотного изменения диэлектрических потерь с учетом вкладов релаксационного механизма и электропроводности кристалла [3]. Наблюдение максимума на кривой tgd (f) свидетельствует о релаксационных потерях в GaSe, а наличие одного максимума говорит о том, что монокристалл GaSe имеет одно время релаксации.
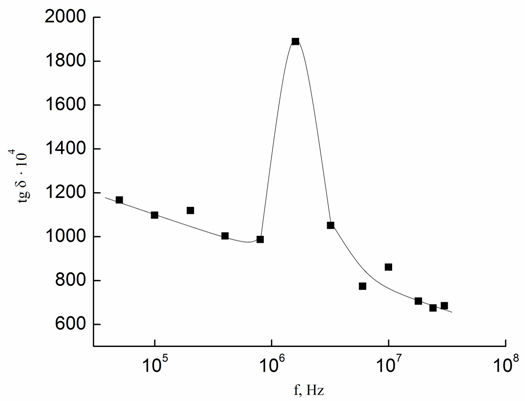
Рис. 3. Зависимость тангенса угла диэлектрических потерь в монокристалле GaSe от частоты.
На рис. 4 представлены экспериментальные результаты изучения частотно-зависимой ac-проводимости монокристалла GaSe при 300 K.
В частотной области 105–3.5´107 ac-проводимость монокристалла GaSe изменялась по закону σac ~ f s, где s = 0.8. Как известно, ac-проводимость зонного типа является в основном частотно-независимой вплоть до 1010–1011 Гц. Наблюдаемая нами экспериментальная зависимость sac ~ f 0.8 свидетельствует о том, что она обусловлена прыжками носителей заряда между локализованными в запрещенной зоне состояниями.
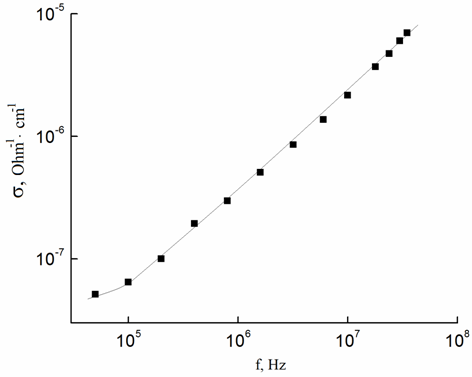
Рис. 4. Частотно-зависимая ас-проводимость монокристалла GaSe при T = 300 K.
Это могут быть локализованные вблизи краев разрешенных зон состояния или локализованные вблизи уровня Ферми состояния [4]. Но так как в экспериментальных условиях проводимость по состояниям вблизи уровня Ферми всегда доминирует над проводимостью по состояниям вблизи краев разрешенных зон, полученный нами закон sac ~ f 0.8 свидетельствует о прыжковом механизме переноса заряда по состояниям, локализованным в окрестности уровня Ферми [5]:
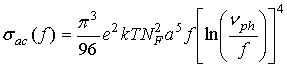 , (1)
, (1)
где e – заряд электрона; k – постоянная Больцмана; NF – плотность состояний вблизи уровня Ферми; a = 1/a – радиус локализации; a – постоянная спада волновой функции локализованного носителя заряда y ~ e–ar; nph – фононная частота.
Согласно
формуле (1) ac-проводимость зависит от
частоты как ![]() ,
т.е. при f << nph
величина sac
приблизительно пропорциональна f
0.8.
,
т.е. при f << nph
величина sac
приблизительно пропорциональна f
0.8.
С помощью формулы (1) по экспериментально найденным значениям σac(f) вычислили плотность состояний на уровне Ферми. Вычисленное значение NF для монокристалла GaSe составляло NF = 1.3´1018 эВ–1×cм–3. При вычислениях NF для радиуса локализации взято значение a = 34 Å, полученное экспериментально для монокристалла GaSe из dc-измерений [2]. Значение nph взято равным 1012 Гц.
Согласно теории прыжковой проводимости на переменном токе среднее расстояние прыжков (R) определяется по следующей формуле
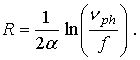 (2)
(2)
Вычисленное по формуле (2) значение R для монокристалла GaSe составляло 197 Å. Это значение R примерно в 6 раз превышает среднее расстояние между центрами локализации носителей заряда в монокристалле GaSe. Значение R позволило по формуле
t –1 = nph · exp(–2aR) (3)
определить среднее время прыжков в монокристалле GaSe: τ = 0.1 мкс.
По формуле [4]
![]() (4)
(4)
в монокристалле GaSe оценен разброс локализованных вблизи уровня Ферми состояний: ∆ Е = 0.048 эВ. А по формуле:
Nt = NF × DE (5)
определена концентрация глубоких ловушек в монокристалле GaSe, ответственных за ac-проводимость: Nt = 6.2´1016 cм–3.
При
переносе заряда вследствие прыжковой проводимости по локализованным в
запрещенной зоне состояниям следует учитывать, что эти локализованные
состояния, случайным образом распределенные в объеме образца, разделены
энергетическим барьером. Величина параметра s в частотной зависимости ac-проводимости
позволяет оценить разницу энергий между основным состоянием в энергетическом
минимуме и свободным состоянием, в котором носитель может перемещаться по
кристаллу [6]
![]() (6)
(6)
Расчеты
показывают, что в образце GaSe Wm = 0.77
эВ. Полученное значение Wm и
значение диэлектрической проницаемости монокристалла GaSe в области высоких
частот, при которых имеет место f
0.8–закон
для ac-проводимости, позволяют по
формуле
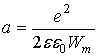 (7)
(7)
(где e0 – диэлектрическая постоянная) определить боровский радиус локализованного носителя заряда а = 32 Å. То есть значения радиуса локализации, полученные из dc и ac-измерений монокристалла GaSe, почти совпадают друг с другом.
Заключение
Таким образом, экспериментальные результаты по изучению частотной дисперсии диэлектрических коэффициентов и проводимости монокристалла GaSe позволили установить природу диэлектрических потерь, механизм переноса заряда, оценить параметры локализованных состояний, такие как плотность состояний вблизи уровня Ферми и их разброс, среднее время и расстояние прыжков, а также концентрацию глубоких ловушек, ответственных за проводимость на переменном токе.
ЛИТЕРАТУРА
1. Мустафаева С.Н., Асадов М.М. Прыжковая проводимость в монокристаллах p - GaSe // Неорганические материалы. 1988. Т. 24 № 6. С. 917–920.
2. Мустафаева С.Н. Прыжковая проводимость в монокристаллах p-GaSe на постоянном токе // Неорганические материалы. 1994. Т. 30. № 5. С. 619–621.
3. Пасынков В.В., Сорокин В.С. Материалы электронной техники. М.: Высшая школа. 1986. 368 с.
4. Мотт Н., Дэвис Э. Электронные процессы в некристаллических веществах. М.: Мир 1974. 472 c.
5. Pollak M. Frequency dependence of conductivity in amorphous solids // Phil. Mag. 1971. V. 23. P. 519–542.
6. Балашова Е.В., Кричевцов Б.Б., Леманов В.В. Диэлектрическая проницаемость и проводимость пленок триглицинсульфата на подложках Al/SiO2 и a-Al2O3 // ФТТ. 2010. Т. 52. № 1. С. 119–123.