УДК: 57.02.001.57
АНАЛИЗ СПЕКТРА КВАЗИПЕРИОДИЧЕСКИХ ИМПУЛЬСОВ ЭЛЕКТРОМИОГРАММЫ
А. М. Шайдук, С. А. Останин
ГОУ ВПО «Алтайский государственный университет», г. Барнаул
Получена 27 июня 2011 г.
Аннотация. Аналитически получена функция средней спектральной мощности сигнала поверхностной элекромиограммы, которая сформирована квазипериодической последовательностью потенциалов действия. Приведены результаты численного моделирования средней спектральной мощности. Проанализирована структура спектра мощности элекромиограммы.
Ключевые слова: поверхностная электромиография, спектральный анализ случайных сигналов, квазипериодические сигналы.
Abstract. The function of the average spectral power surface electromyography signal, which is formed by a quasi-periodic sequence of action potentials, is derived analytically. The results of numerical simulation of the average spectral power are presented. The analysis of the structure of the power spectrum surface electromyography is carried out.
Keywords: surface electromyography, spectral analysis of random signals, quasi-periodic signals.
Интерференционная электромиография является неинвазивным методом исследования нервно-мышечной системы биологических объектов [1]. Сложность анализа электромиограмм, полученных с помощью поверхностных электродов, обуславливается хаотическим характером изменения во времени разности потенциалов действия большого количества отдельных двигательных единиц. Для количественного анализа таких сигналов используют, например, методы спектрального анализа [2-4].
Процесс генерации потенциалов действия является лишь
квазипериодическим процессом, в котором временные промежутки ![]() между соседними
между соседними ![]() и
и ![]() импульсами являются случайными
величинами. Если
импульсами являются случайными
величинами. Если ![]() ,
время запуска
,
время запуска ![]() -го
импульса есть
-го
импульса есть ![]() ,
,
![]() , то импульсы
следуют регулярно, спектр такого электромиосигнала рассмотрен в [4].
, то импульсы
следуют регулярно, спектр такого электромиосигнала рассмотрен в [4].
Если импульсы ПДОДЕ следуют друг за другом
нерегулярно, ![]() является
случайной величиной. В этом случае время запуска
является
случайной величиной. В этом случае время запуска ![]() -го импульса есть
-го импульса есть ![]() тоже случайная величина
тоже случайная величина
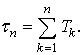 (1)
(1)
Этот случай рассмотрен в работе [2].
Обратимся теперь к структуре спектра, если время
генерации отдельного сигнала жестко привязана к некоторой «временной сетке» с
узлами ![]() ,
допуская некоторые случайные сдвиги
,
допуская некоторые случайные сдвиги ![]() . Иными словами, теперь, в отличие от (1),
время запуска
. Иными словами, теперь, в отличие от (1),
время запуска ![]() -го
импульса
-го
импульса ![]() :
:
Как будет показано ниже, при этом структура спектра сигнала существенно изменяется.
Пусть зависимость напряжения от времени для потенциала
действия отдельной двигательной единицы (ПДОДЕ) есть функция ![]() . Электромиографический
сигнал
. Электромиографический
сигнал ![]() ,
представляет собой сумму отдельных потенциалов действия, сдвинутыми
относительно условного нулевого сигнала на время
,
представляет собой сумму отдельных потенциалов действия, сдвинутыми
относительно условного нулевого сигнала на время ![]()
где ![]() – полное число отдельных импульсов ПДОДЕ,
генерируемое за время измерения электромиограммы.
– полное число отдельных импульсов ПДОДЕ,
генерируемое за время измерения электромиограммы.
Определим спектральную функцию ![]() сигнала
сигнала ![]() .
.
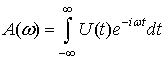 (4)
(4)
Из известных свойств преобразования
Фурье сразу следует, что если в качестве функции ![]() использовать ее представление в виде (3),
то
использовать ее представление в виде (3),
то
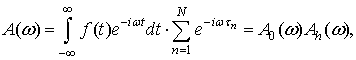 (5)
(5)
где
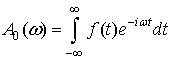
спектральная функция импульса ПДОДЕ и
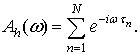 (6)
(6)
Используя соотношение (2), для
функции ![]() получаем
получаем
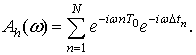 (7)
(7)
Спектр ![]() является случайной величиной и изменяется
от реализации к реализации. Выражение (7) для какой-либо случайной реализации
может быть разыграно, если известны статистические свойства случайной
последовательности
является случайной величиной и изменяется
от реализации к реализации. Выражение (7) для какой-либо случайной реализации
может быть разыграно, если известны статистические свойства случайной
последовательности ![]() .
Можно, однако, оценить его статистические характеристики.
.
Можно, однако, оценить его статистические характеристики.
Пусть плотность вероятности появления значения ![]() есть
есть ![]() , т.е. вероятность
появления значения
, т.е. вероятность
появления значения ![]() есть
есть
![]() .
.
Тогда математическое ожидание спектральной функции есть
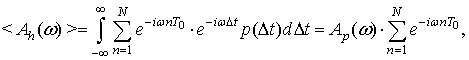 (8)
(8)
где
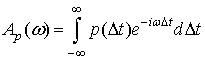 (9)
(9)
спектральная функция плотности вероятности. Выполняя суммирование в выражении (8), получаем окончательно
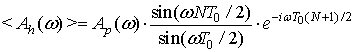 (10)
(10)
и, следовательно, спектральная
функция электромиосигнала типа (3) полностью определяется спектральной функцией
![]() отдельной
двигательной единицы и спектральной функцией
отдельной
двигательной единицы и спектральной функцией ![]() плотности вероятности
плотности вероятности ![]() появления величины
появления величины ![]() .
.
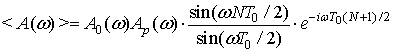 (11)
(11)
Измеряемая спектральная мощность сигнала есть
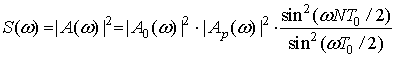 (12)
(12)
Соотношения (11) и (12) решают
проблему нахождения спектра сигнала типа (3). Если вид функции ![]() известен, то в
некоторых случаях можно получить и соответствующие аналитические соотношения.
Однако следует отметить, что в эксперименте обычно измеряется спектральная
мощность сигнала
известен, то в
некоторых случаях можно получить и соответствующие аналитические соотношения.
Однако следует отметить, что в эксперименте обычно измеряется спектральная
мощность сигнала ![]() .
Поэтому практически получить спектр типа (11), усредненный по множеству
реализаций, в этом случае не удастся. Экспериментально гораздо естественнее
получать усредненную по реализациям спектральную мощность сигнала
.
Поэтому практически получить спектр типа (11), усредненный по множеству
реализаций, в этом случае не удастся. Экспериментально гораздо естественнее
получать усредненную по реализациям спектральную мощность сигнала ![]() . В силу
некоммутативности операции усреднения и операции квадрата модуля результат
такого усреднения будет принципиально отличаться от соотношения (12).
. В силу
некоммутативности операции усреднения и операции квадрата модуля результат
такого усреднения будет принципиально отличаться от соотношения (12).
Вычислим теперь величину ![]() , усредняя не функцию (7), а спектральную
мощность сигнала. Спектральная мощность одной реализации сигнала есть квадрат
модуля соотношения (6).
, усредняя не функцию (7), а спектральную
мощность сигнала. Спектральная мощность одной реализации сигнала есть квадрат
модуля соотношения (6).
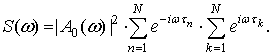 (13)
(13)
где параметр ![]() определяется соотношением (2).
Соотношение (13) (без сомножителя
определяется соотношением (2).
Соотношение (13) (без сомножителя ![]() ) представляет собой сумму
) представляет собой сумму ![]() слагаемых
слагаемых ![]() , которые представляют
собой выражения типа
, которые представляют
собой выражения типа
![]() (14)
(14)
Рассмотрим матрицу, составленную из выражений ![]()
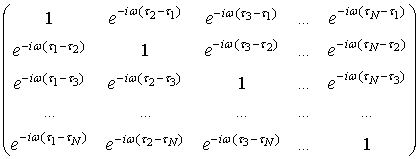 (15)
(15)
Спектральная мощность ![]() одной реализации в силу
соотношения (13) есть просто сумма всех элементов матрицы (15), умноженная на
одной реализации в силу
соотношения (13) есть просто сумма всех элементов матрицы (15), умноженная на ![]() . В силу линейности
оператора усреднения средняя спектральная мощность
. В силу линейности
оператора усреднения средняя спектральная мощность ![]() является суммой средних значений
элементов матрицы (15) (умноженной на
является суммой средних значений
элементов матрицы (15) (умноженной на ![]() ).
).
Вычислим математическое ожидание элемента ![]() .
.
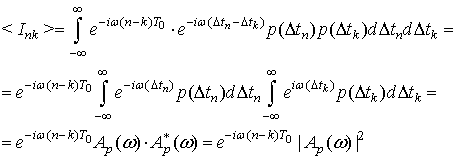 (16)
(16)
Матрица (15), составлена теперь из
средних значений ![]() ,
и среднее значение случайного сомножителя в (13) равна сумме элементов этой
матрицы.
,
и среднее значение случайного сомножителя в (13) равна сумме элементов этой
матрицы.
Таким образом, средний спектр мощности сигнала типа
(3) вновь полностью определяется спектральной характеристикой ![]() отдельного импульса и
спектральной функцией
отдельного импульса и
спектральной функцией ![]() плотности
вероятности
плотности
вероятности ![]() случайной
величины
случайной
величины ![]() .
.
Выполняя подиагональное
суммирование элементов указанной матрицы, составленной уже из средних значений ![]() , получаем
, получаем
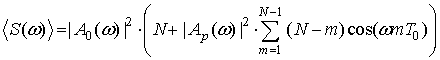 (17)
(17)
Соотношение (17) и решает поставленную проблему определения спектральной мощности, усредненной по реализациям.
Видно, что выражение (17) существенно отличается и от
соотношения (12). Для получения конкретных аналитических выражений, необходимо
определить тип статистики. Например, если распределение случайной величины ![]() является гауссовским,
т.е. подчиняется распределению
является гауссовским,
т.е. подчиняется распределению
![]() (18)
(18)
то величина ![]() есть
есть
![]() (19)
(19)
Подставляя выражение (19) в (17) получаем окончательно
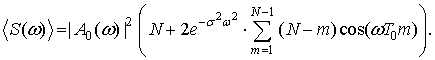 (20)
(20)
Соотношение (20) и позволяет вычислить спектр мощности сигнала типа (3), усредненный по большому числу реализаций для гауссовской статистики (нормального распределения).
Из соотношения (20) видно, что при ![]() всегда возникает спектральная
линия, мощность которой пропорциональна
всегда возникает спектральная
линия, мощность которой пропорциональна ![]() . Это, конечно, очевидный результат,
поскольку при нулевой частоте хаотичность следования импульсов не имеет
никакого значения и это сразу видно из соотношения (5).
. Это, конечно, очевидный результат,
поскольку при нулевой частоте хаотичность следования импульсов не имеет
никакого значения и это сразу видно из соотношения (5).
Если дисперсия ![]() , то из (20) сразу получается известный из
теории дифракции набор эквидистантных спектральных линий одинаковой мощности на
частотах
, то из (20) сразу получается известный из
теории дифракции набор эквидистантных спектральных линий одинаковой мощности на
частотах
 (21)
(21)
Если дисперсия ![]() , то наиболее
интенсивной является первая спектральная линия
, то наиболее
интенсивной является первая спектральная линия ![]() , мощность которой определяется дисперсией
(при увеличении дисперсии мощность быстро уменьшается). Интенсивность линий
более высоких порядков быстро уменьшается и при достаточно больших
, мощность которой определяется дисперсией
(при увеличении дисперсии мощность быстро уменьшается). Интенсивность линий
более высоких порядков быстро уменьшается и при достаточно больших ![]() усредненный по
реализациям спектр мощности перестает зависеть от
усредненный по
реализациям спектр мощности перестает зависеть от ![]() и стремится к постоянному значению
и стремится к постоянному значению ![]() .
.
На рисунке 1 приведен результат численного моделирования
и вычисления спектральной мощности для достаточно малой дисперсии ![]() . Для сравнения на
рисунке 2 приведен спектр мощности при другом типе управления временем
следования импульсов (1).
. Для сравнения на
рисунке 2 приведен спектр мощности при другом типе управления временем
следования импульсов (1).
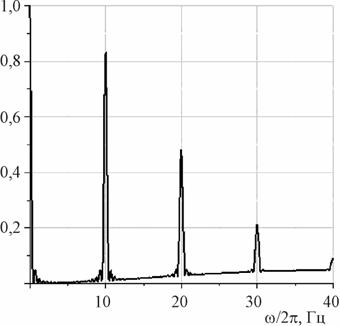
Рис. 1. Спектр мощности,
усредненный по реализациям для импульсов, привязанных к решетке. Дисперсия ![]() , средний период
, средний период ![]() , число одиночных импульсов
, число одиночных импульсов ![]() .
.
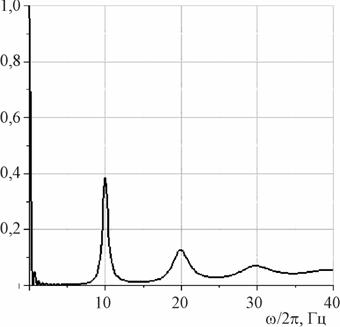
Рис. 2. Спектр мощности,
усредненный по реализациям. Дисперсия ![]() , средний период
, средний период ![]() , число одиночных
импульсов
, число одиночных
импульсов ![]() .
.
При случайном запуске импульсов, подчиняющемся соотношению (2), спектральные линии имеют большую относительную интенсивность и их ширина практически не зависит от номера спектральной линии. В противоположность этому, ширина спектральных линий при управлении запуском импульсов типа (1) увеличивается с ростом номера наблюдаемой линии. Этот факт можно использовать при анализе экспериментально наблюдаемых спектров для определения типа управления временем запуска импульсов.
На рисунках 3 и 4 показаны контуры первых спектральных линий для различных количеств импульсов в исходном сигнале.
Из сравнения рисунков 3 и 4 ясно, что ширина
спектральной линии определяется главным образом количеством одиночных импульсов
в исследуемом сигнале и с ростом числа импульсов ширина спектральной линии
уменьшается. Это дает принципиальную возможность, измеряя ширину линии, оценить
количество импульсов ![]() .
Если количество импульсов
.
Если количество импульсов ![]() примерно известно, то мы можем указать
область спектра, где следует искать первую спектральную линию
примерно известно, то мы можем указать
область спектра, где следует искать первую спектральную линию
![]() (22)
(22)
где ![]() – длительность исследуемого сигнала.
Условие (22) может сильно упростить анализ спектра при малом количестве
реализаций, когда в наблюдаемом спектре имеется большое количество интенсивных
спектральных линий, имеющих случайную природу. К сожалению, при другом типе
управления следованием импульсами (1) оценить количество импульсов
– длительность исследуемого сигнала.
Условие (22) может сильно упростить анализ спектра при малом количестве
реализаций, когда в наблюдаемом спектре имеется большое количество интенсивных
спектральных линий, имеющих случайную природу. К сожалению, при другом типе
управления следованием импульсами (1) оценить количество импульсов ![]() по ширине
спектральной линии не удается.
по ширине
спектральной линии не удается.
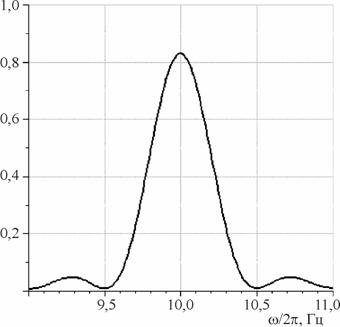
Рис. 3. Контур первой
линии, усредненный для импульсов, привязанных к решетке. Дисперсия ![]() , средний период
, средний период ![]() , число одиночных импульсов
, число одиночных импульсов ![]() .
.
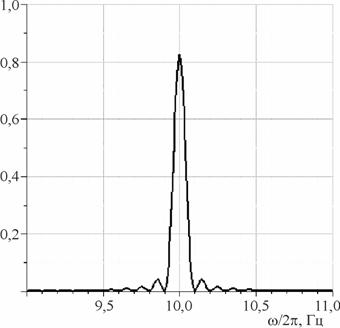
Рис. 4. Контур первой
линии, усредненный для импульсов, привязанных к решетке. Дисперсия ![]() , средний период
, средний период ![]() , число одиночных импульсов
, число одиночных импульсов ![]() .
.
В качестве примера, на рисунках 5 и 6 показаны контуры первых спектральных линий при времени запуска импульсов типа (3) для различных количеств импульсов в исходном сигнале.
Ширина спектральной линии в этом случае вообще не зависит от количества импульсов в исходном сигнале, что и показывает сравнение рисунков 5 и 6. Ширина спектральной линии здесь определяется типом статистики «периода» следования импульсов. При гауссовской статистике ширина спектральной линии определяется дисперсией временного промежутка между импульсами.
Отметим, что это дает принципиальную возможность оценки величины дисперсии по ширине наблюдаемой спектральной линии.
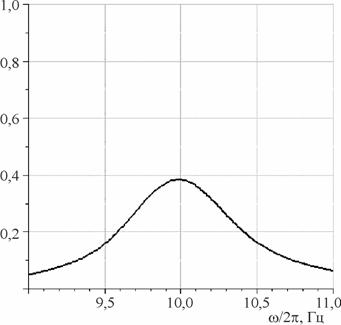
Рис. 5. Контур первой
линии, усредненный по реализациям. Дисперсия ![]() , средний период
, средний период ![]() , число одиночных импульсов
, число одиночных импульсов ![]() .
.
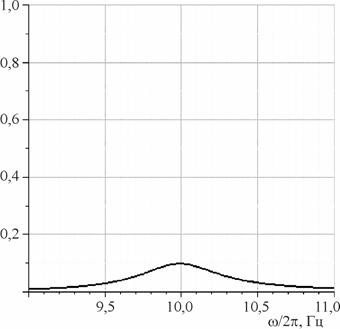
Рис. 6. Контур первой
линии, усредненный по реализациям. Дисперсия ![]() , средний период
, средний период ![]() , число одиночных импульсов
, число одиночных импульсов ![]() .
.
Оценим, при какой дисперсии даже первая линия в
спектре мощности может быть недостаточно интенсивной для ее обнаружения. Для
первой линии ![]() ,
отсюда
,
отсюда
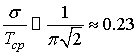 .
.
Если дисперсия ![]() , первая спектральная линия в
одной реализации спектра сигнала типа (3) сравнима по мощности со случайно
возникающими спектральными линиями и вероятность неверного определения средней
частоты следования импульсов (или среднего периода
, первая спектральная линия в
одной реализации спектра сигнала типа (3) сравнима по мощности со случайно
возникающими спектральными линиями и вероятность неверного определения средней
частоты следования импульсов (или среднего периода ![]() ) может стать неприемлемо
большой.
) может стать неприемлемо
большой.
ЛИТЕРАТУРА
1. Физиология человека / Под ред. Косицкого Г.И. – М.: Медицина, 1985. – 544 с.
2. Рангайян Р.М. Анализ биомедицинских сигналов. Практический подход – Пер. с англ. под ред. А.П. Немирко – М.: ФИЗМАТЛИТ. – 2007. – 440 с.
3. Kaplanis P.A., Pattichis C.S., Hadjileontiadis L.J. Surface EMG analysis on normal subjects based on isometric voluntary contraction // Journal of Electromyography and Kinesiology – 2009. – No. 19. p. 157–171.
4. Шайдук А.М., Останин С.А. Моделирование электромиографического сигнала средствами LabVIEW. Известия Алтайского государственного университета. – Барнаул: Изд.-во АлтГУ – Ч.1(65), 2010. – С. 195 – 201.
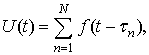 (3)
(3)