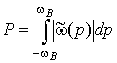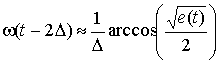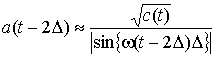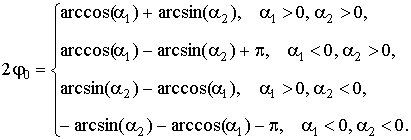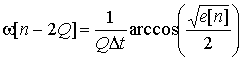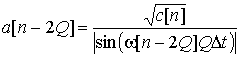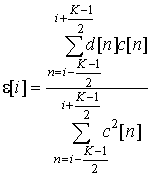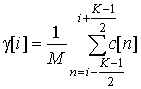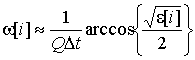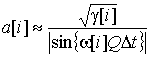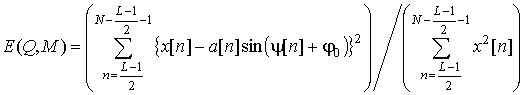УДК 53.083
ОПРЕДЕЛЕНИЕ ЭЛЕКТРОДИНАМИЧЕСКИХ ПАРАМЕТРОВ НЕСТАЦИОНАРНЫХ СИСТЕМ
В. К. Игнатьев, А. В. Никитин, С. В. Юшанов
Волгоградский государственный университет, кафедра радиофизики
Получена 27 июля 2011 г.
Аннотация. Описан цифровой параметрический алгоритм выделения огибающей и мгновенной частоты квазигармонического сигнала. Приведены условия их однозначной связи с физическими параметрами нестационарной системы, являющейся источником сигнала. Проведены эксперименты с нестационарной системой, представляющей собой колебательный контур с переменной емкостью. По отклику этой системы на гармоническое воздействие с высокой точностью восстановлен закон изменения емкости.
Ключевые слова: медленно меняющиеся параметры, обратная задача, косвенные измерения, квазигармонический сигнал, мгновенная частота, огибающая.
Abstract. The digital parametric algorithm of allocation the envelope and instantaneous frequency of a quasiharmonic signal is described. The conditions of their unique physical properties due to the time-dependent system which are a source of a signal are resulted. Experiments with time-dependent system, which is an oscillatory circuit with variable capacitance, are executed. The variation of capacity restored with high precision by the response of the system in a harmonious signal.
Key words: slowly varying parameters, inverse problem, indirect measurements, oscillatory circuit, quasi-harmonic signal, instantaneous frequency, envelope.
Введение
Многие физические задачи сводятся к косвенному измерению параметров нестационарных систем, динамика которых описывается линейным уравнением второго порядка вида
К таким уравнениям приводит задача о распространении гармонической волны в неоднородной среде, собственных колебаниях кварцевого резонатора при изменении температуры кристалла, и другие [1]. Например, в ЯМР известны уравнения Блоха для поперечных проекций магнитного момента [2]:
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
из которых легко получается
уравнение для свободной прецессии поперечной намагниченности в медленно
меняющемся продольном магнитном поле ![]() в
виде (1) (
в
виде (1) (![]() – гиромагнитное
отношение). В этом случае
– гиромагнитное
отношение). В этом случае ![]() или
или ![]() ,
,
![]() ,
, ![]() ,
, ![]() . Если по измеренному сигналу
. Если по измеренному сигналу ![]() восстановить коэффициенты
восстановить коэффициенты ![]() и
и ![]() , можно проследить за динамикой изменения
магнитного поля
, можно проследить за динамикой изменения
магнитного поля ![]() и времени поперечной релаксации
и времени поперечной релаксации ![]() , что важно в задачах спектроскопии,
томографии, исследовании геомагнитного поля и других.
, что важно в задачах спектроскопии,
томографии, исследовании геомагнитного поля и других.
Определение неизвестных параметров ![]() и
и ![]() уравнения
(1) по измеренному сигналу
уравнения
(1) по измеренному сигналу ![]() при известном воздействии
при известном воздействии ![]() является коэффициентной
обратной задачей [3]. Часто в качестве
является коэффициентной
обратной задачей [3]. Часто в качестве ![]() используют гармоническое колебание, тогда, если параметры
системы медленно меняются по отношению к периоду собственных колебаний, исследуемый
сигнал в общем случае представляют в виде квазигармонического колебания [4,
5]
используют гармоническое колебание, тогда, если параметры
системы медленно меняются по отношению к периоду собственных колебаний, исследуемый
сигнал в общем случае представляют в виде квазигармонического колебания [4,
5]
огибающая ![]() и мгновенная
частота
и мгновенная
частота ![]() которого определенным образом связаны с параметрами нестационарной
системы и являются медленно меняющимися функциями. При этом функции
которого определенным образом связаны с параметрами нестационарной
системы и являются медленно меняющимися функциями. При этом функции ![]() и
и ![]() будут взаимнооднозначно связаны с
исследуемым колебанием
будут взаимнооднозначно связаны с
исследуемым колебанием ![]() .
В работе [6] показано, что если огибающей и мгновенной частоте сопоставляются измеряемые
физические величины, условие единственности квазигармонического представления
(2) можно записать в виде
.
В работе [6] показано, что если огибающей и мгновенной частоте сопоставляются измеряемые
физические величины, условие единственности квазигармонического представления
(2) можно записать в виде
где
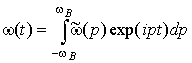 ,
,
а ![]() – частота,
которой ограничен спектр
– частота,
которой ограничен спектр ![]() мгновенной
частоты. При таком условии на мгновенную частоту сигнал (2) может быть
достаточно широкополосным несмотря на медленность изменения огибающей и
частоты.
мгновенной
частоты. При таком условии на мгновенную частоту сигнал (2) может быть
достаточно широкополосным несмотря на медленность изменения огибающей и
частоты.
На основании условия (3) единственности представления
исследуемого колебания в виде (2) можно построить методы измерения параметров
нестационарной системы, описываемой уравнением (1), оценивая огибающую ![]() и мгновенную частоту
и мгновенную частоту ![]() .
.
Метод измерения
Для исследуемого сигнала ![]() можно
построить функции следующего вида [6 – 10]:
можно
построить функции следующего вида [6 – 10]:
![]() ,
, ![]() ,
,
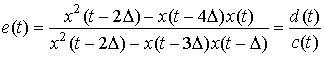 ,
,
где D – некоторый временной интервал, такой, что
Условие (3) медленности изменения мгновенной частоты и огибающей для квазигармонического сигнала (2) запишем следующим образом
![]() ,
, ![]() ,
, ![]() , (5)
, (5)
тогда можно получить выражения для мгновенной
частоты и огибающей, учитывая приближение порядка ![]() [6 –
8]
[6 –
8]
Для полного описания сигнала помимо динамики частоты ![]() и огибающей
и огибающей ![]() требуется также определить
значение начальной фазы
требуется также определить
значение начальной фазы ![]() .
На интервале наблюдения
.
На интервале наблюдения ![]() рассмотрим интеграл от квадрата разности:
рассмотрим интеграл от квадрата разности:
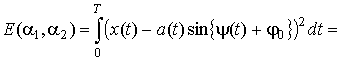
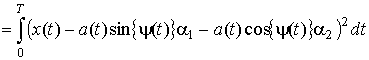 .
.
Здесь ![]() ,
, ![]() , и
, и ![]() . Минимизируя функцию
. Минимизируя функцию ![]() , получим
, получим
![]() ,
, ![]() ,
,
где
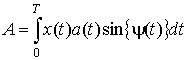 ,
, 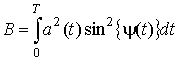 ,
,
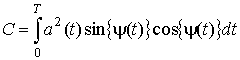 ,
, 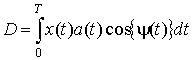 ,
, 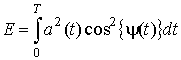 .
.
Теперь можно найти начальную фазу,
учитывая знаки ![]() и
и ![]() :
:
Перейдем к последовательности ![]() (
(![]() ), подвергнув сигнал
), подвергнув сигнал ![]() дискретизации с шагом
дискретизации с шагом ![]() и полагая, что интервал
и полагая, что интервал ![]() может содержать несколько
интервалов
может содержать несколько
интервалов ![]() , то есть
, то есть ![]() ,
, ![]() . Тогда выражения (6) примут вид
. Тогда выражения (6) примут вид
где
![]() ,
, ![]() ,
,
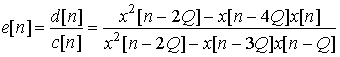 ,
, ![]() .
.
Начальную фазу можно найти в
соответствии с выражениями (7), минимизируя ![]() и вычисляя
и вычисляя ![]() и
и ![]() :
:
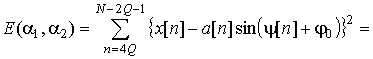
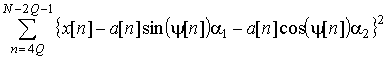 ,
,
где
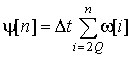 ,
, ![]() ,
, ![]() ,
,
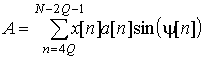 ,
, 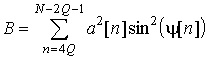 ,
,
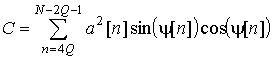 ,
, 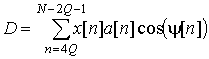 ,
, 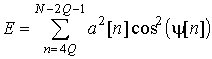 .
.
Поскольку отклик исследуемой системы содержит аддитивный
шум, при использовании описываемого метода имеет смысл применять, например,
метод наименьших квадратов (МНК), то есть получать один отсчет огибающей и
частоты на некотором интервале. Перепишем выражения (8), взяв для получения
одного отсчета оценок ![]() и
и ![]() скользящее окно длиной
скользящее окно длиной ![]() . Здесь
. Здесь ![]() – количество 5-точечных интервалов
длиной
– количество 5-точечных интервалов
длиной ![]() , смещенных друг
относительно друга на
, смещенных друг
относительно друга на ![]() ,
по которым ведется усреднение при получении одного значения
,
по которым ведется усреднение при получении одного значения ![]() и
и ![]() :
:
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
Обозначим ![]() и
и ![]() оценки
оценки ![]() и
и ![]() , полученные на интервале длиной
, полученные на интервале длиной ![]() c номером
c номером ![]() .
Рис. 1 иллюстрирует этот процесс, разным цветом выделены отсчеты
.
Рис. 1 иллюстрирует этот процесс, разным цветом выделены отсчеты ![]() , участвующие в оценке на
, участвующие в оценке на ![]() -м шаге. В соответствии с МНК получаем:
-м шаге. В соответствии с МНК получаем:
.
Заметим, что при коэффициенте прореживания ![]() числитель и знаменатель первого выражения
и второе выражение (9) можно представить в виде рекурсии, что существенно сократит
объем вычислений и облегчит реализацию данного алгоритма в устройстве на базе
сигнального процессора. Для числителя первого выражения эта рекурсия будет
иметь вид
числитель и знаменатель первого выражения
и второе выражение (9) можно представить в виде рекурсии, что существенно сократит
объем вычислений и облегчит реализацию данного алгоритма в устройстве на базе
сигнального процессора. Для числителя первого выражения эта рекурсия будет
иметь вид
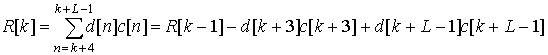 .
.
Аналогично считаются и остальные рекурсии.
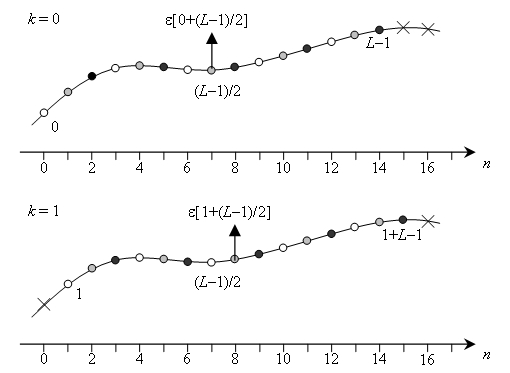
Рис.
1. Получение оценок ![]() и
и
![]() по скользящему окну
по скользящему окну
при ![]() .
.
После вычисления выражений (9) отсчеты частоты и огибающей можно найти в соответствии с (8):
Контролем качества определения зависимостей ![]() и
и ![]() может служить относительная
энергия отклонения восстановленного сигнала от исходного:
может служить относительная
энергия отклонения восстановленного сигнала от исходного:
Исходя из минимизации ![]() , можно подбирать оптимальные
значения коэффициента прореживания
, можно подбирать оптимальные
значения коэффициента прореживания ![]() и
количества усреднений
и
количества усреднений ![]() .
.
Численное моделирование показало принципиальную возможность использования метода для решения обратной коэффициентной задачи [3] на примере уравнения Матье [6, 7]. Если из законов электродинамики может быть получена однозначная связь коэффициентов уравнения (1) с физическими измеряемыми параметрами нестационарной системы, описываемой этим уравнением, предложенный метод позволяет восстановить закон изменения этих параметров.
Экспериментальная установка
Проверка метрологических характеристик метода проводилась на
примере нестационарной системы, принципиальная схема которой приведена на рис.
2. Она представляет собой параллельный колебательный контур, включенный
последовательно с резистором ![]() .
Колебательный контур состоит из катушки индуктивности
.
Колебательный контур состоит из катушки индуктивности ![]() (последовательно с ней изображен
резистор
(последовательно с ней изображен
резистор ![]() – собственное
сопротивление катушки), и соединенных параллельно переменного конденсатора
– собственное
сопротивление катушки), и соединенных параллельно переменного конденсатора ![]() и подстроечного конденсатора
и подстроечного конденсатора ![]() .
.
Нестационарным элементом системы является механический
конденсатор переменной емкости ![]() с воздушным диэлектриком, передний подшипник скольжения
которого заменен на подшипник качения. Катушка индуктивности содержит 1016
витков медного провода диаметром 0,6 мм, намотанного на тороидальном каркасе из
стеклопластика. Пустотелый каркас имеет круглое сечение диаметром 90 мм, его внешний диаметр равен 390 мм, внутренний – 210 мм.
с воздушным диэлектриком, передний подшипник скольжения
которого заменен на подшипник качения. Катушка индуктивности содержит 1016
витков медного провода диаметром 0,6 мм, намотанного на тороидальном каркасе из
стеклопластика. Пустотелый каркас имеет круглое сечение диаметром 90 мм, его внешний диаметр равен 390 мм, внутренний – 210 мм.
Сигнал на исследуемую систему подается через помещенный в
экран трансформатор ![]() с разделительной обмоткой, которая подключена к заземленному
экрану. Катушка индуктивности и обе емкости также помещены в экраны. Связи
между элементами данной цепи обеспечиваются посредством триаксиального кабеля,
внешняя оплетка которого соединена с экранами. Выходной сигнал системы снимается
с конденсатора.
с разделительной обмоткой, которая подключена к заземленному
экрану. Катушка индуктивности и обе емкости также помещены в экраны. Связи
между элементами данной цепи обеспечиваются посредством триаксиального кабеля,
внешняя оплетка которого соединена с экранами. Выходной сигнал системы снимается
с конденсатора.
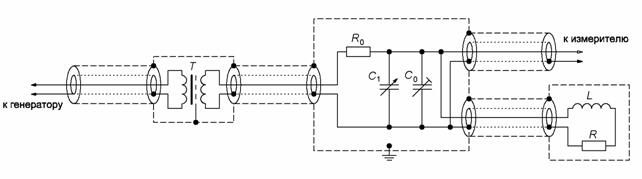
Рис. 2. Принципиальная схема нестационарной системы.
Ось переменного конденсатора вращается электродвигателем, помещенным в заземленный стальной экран для минимизации создаваемых им электромагнитных помех. Вал электродвигателя соединяется с осью конденсатора тросиком через втулки из непроводящего материала (стеклопластика). Тросик также соединен с заземлением с помощью опор, натягивающих его и удерживающих от колебательных движений, которые могут привести к обрыву соединения. Втулка, соединяющая тросик и переменный конденсатор, покрыта слоем медной фольги, которая припаяна к тросику для экранирования наводок на конденсатор. При этом фольга не соприкасается с осью конденсатора. Чертеж кинематической схемы установки приведен на рис. 3. Электродвигатель питается от источника постоянного напряжения 25 В, скорость его вращения контролируется с помощью бесконтактного цифрового тахометра/стробоскопа АКТАКОМ АТТ-6002 [11].
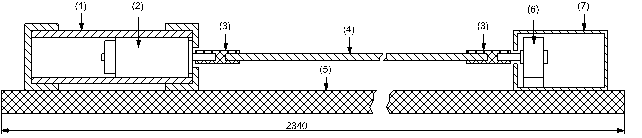
Рис. 3. Кинематическая схема нестационарной системы: 1 – экран,
2 – электродвигатель, 3 – втулка (стеклопластик), 4 – тросик,
5 – станина (дерево), 6 – переменный конденсатор, 7 – экран.
Параметры колебательной системы (в первую очередь – подстроечного
конденсатора ![]() ) подобраны
таким образом, чтобы резонанс наблюдался на частоте
) подобраны
таким образом, чтобы резонанс наблюдался на частоте ![]() кГц
при максимальном сближении обкладок переменного конденсатора. На эту же частоту
настроен внешний генератор гармонического сигнала
кГц
при максимальном сближении обкладок переменного конденсатора. На эту же частоту
настроен внешний генератор гармонического сигнала ![]() с
частотой
с
частотой ![]() .
.
На рис. 4 изображена эквивалентная схема колебательного
контура, в соответствии с которой производились все расчеты. На этой схеме следующие
номиналы элементов: ![]() мГн,
мГн, ![]() Ом,
Ом, ![]() МОм,
МОм, ![]() пФ, а переменная емкость
пФ, а переменная емкость ![]() меняется в пределах 3,1…18,3 пФ.
Емкость соединительных проводов, а также сопротивление катушки индуктивности
рассчитаны через АЧХ контура и учтены в указанных параметрах системы.
меняется в пределах 3,1…18,3 пФ.
Емкость соединительных проводов, а также сопротивление катушки индуктивности
рассчитаны через АЧХ контура и учтены в указанных параметрах системы.
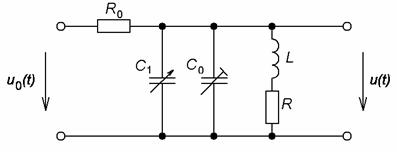
Рис. 4. Эквивалентная схема исследуемой системы.
Изменение переменной емкости производилось с частотой 4000 об/мин, что составляет около 66,67 Гц, тем самым было соблюдено условие на медленность изменения параметров системы
![]() ,
, ![]() .
.
Исследуемый сигнал ![]() подается на 16-разрядный аналого-цифровой преобразователь
(АЦП) ADS1602 [12], который осуществляет его
дискретизацию с шагом
подается на 16-разрядный аналого-цифровой преобразователь
(АЦП) ADS1602 [12], который осуществляет его
дискретизацию с шагом ![]() мкс. АЦП
тактируется с частотой 10 МГц сигналом рубидиевого
генератора Ч1-1013. Входной сигнал
мкс. АЦП
тактируется с частотой 10 МГц сигналом рубидиевого
генератора Ч1-1013. Входной сигнал ![]() также формируется этим генератором с помощью синтезатора
частот AD9833 [13]. Последовательность из N = 32768
отсчетов сигнала передается в компьютер для обработки.
также формируется этим генератором с помощью синтезатора
частот AD9833 [13]. Последовательность из N = 32768
отсчетов сигнала передается в компьютер для обработки.
Результаты эксперимента
Колебательный контур с переменной емкостью ![]() описывается уравнением, аналогичным (1)
описывается уравнением, аналогичным (1)
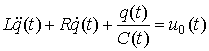 ,
,
где ![]() – заряд на конденсаторе с емкостью
– заряд на конденсаторе с емкостью ![]() . Если
. Если ![]() , то решение
для напряжения можно записать в виде [4, 5]:
, то решение
для напряжения можно записать в виде [4, 5]:
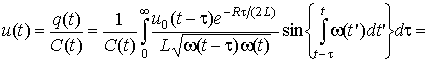
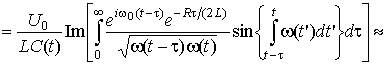
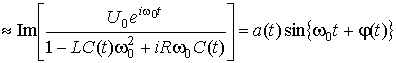 ,
,
где ![]() – характерное время медленного изменения
параметров системы. Здесь обозначено
– характерное время медленного изменения
параметров системы. Здесь обозначено
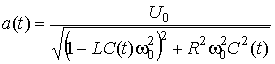 ,
,
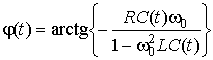 .
.
Значение емкости отсюда легко определить как
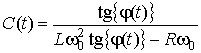 .
(12)
.
(12)
Предлагаемый метод определяет
мгновенную частоту, которая будет равна ![]() , поэтому для определения емкости
необходимо проинтегрировать найденную частоту за вычетом постоянной
составляющей
, поэтому для определения емкости
необходимо проинтегрировать найденную частоту за вычетом постоянной
составляющей ![]() . Для дискретных
значений переменной емкости при нахождении интеграла методом прямоугольников, получим:
. Для дискретных
значений переменной емкости при нахождении интеграла методом прямоугольников, получим:
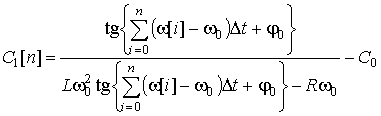 ,
,
![]() ,
,
где значения частоты ![]() рассчитаны по формуле из (10), а
постоянная интегрирования – начальная фаза
рассчитаны по формуле из (10), а
постоянная интегрирования – начальная фаза ![]() .
.
На рис. 5 представлена полученная зависимость переменной емкости
от угла поворота ![]() , а точками обозначены значения, которые были измерены заранее цифровым
измерителем E7-8 [14] с
шагом угла 6º. Видно, что они лежат на графике полученной
зависимости, что говорит о правильности работы метода.
, а точками обозначены значения, которые были измерены заранее цифровым
измерителем E7-8 [14] с
шагом угла 6º. Видно, что они лежат на графике полученной
зависимости, что говорит о правильности работы метода.
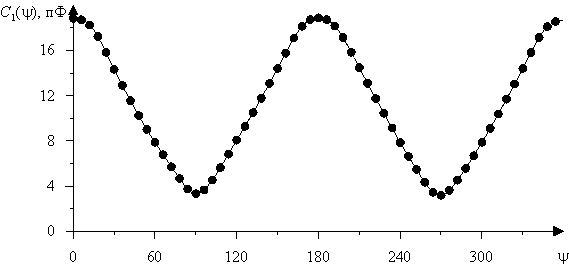
Рис.
5. Полученная зависимость переменной емкости от угла поворота ![]()
(точками обозначены измеренные заранее значения)
Отметим, что отношение сигнал/шум для наблюдаемого сигнала составило 50 дБ, а среднеквадратичное относительное отклонение измеренной емкости от расчетной на периоде изменения емкости приблизительно 10–5.
Такое отклонение находится на уровне точности измерения емкости RLC измерителем, поэтому сложно сказать, что вносит больший вклад в погрешность – метод измерения или неточность изначальных данных для сравнения. Во всяком случае, можно утверждать, что полученная точность достаточно высока для подобных измерений, а рассмотренный метод обеспечивает необходимые для измерительных систем высшего класса точности метрологические характеристики.
Работа поддержана грантом РФФИ 10-07-9713р_а.
Литература
1. Митропольский Ю.А. Проблемы асимптотической теории нестационарных колебаний. – М.: Наука, 1964. – 432 с.
2. Квантовая радиофизика / под ред. В.И. Чижика. СПб.: Изд-во СПбГУ, 2004. – 690 с.
3. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. – М.: Наука, 1979. – 286 с.
4. Гоноровский И.С. Радиотехнические цепи и сигналы. – М.: «Сов. радио», 1977. – 608 с.
5. Вакман Д.Е. Асимптотические методы в линейной радиотехнике. – М.: Советское радио, 1962. – 248 с.
6. Игнатьев В.К., Никитин А.В., Юшанов С.В. Параметрический анализ колебаний с медленно меняющейся частотой // Известия вузов. Радиофизика. – 2010. Т. LIII – № 2. С. 145 – 159.
7. Игнатьев В.К., Никитин А.В., Юшанов С.В. Оценивание медленно меняющихся параметров электромеханических систем // Изв. вузов. Электромеханика. – 2009. – № 2. – С. 28.
8. Игнатьев В.К., Никитин А.В., Хоружий Д.Н., Юшанов С.В. Динамический метод сличения частот // Измерительная техника. – 2011. – № 1. – С. 32.
9. Никитин А.В., Юшанов С.В. Оценивание мгновенной частоты широкополосных сигналов с медленно меняющимися амплитудой и фазой на основе метода Прони // Физика волновых процессов и радиотехнические системы. – 2006. – Т. 9. – № 2. – С. 57.
10. Никитин А.В., Юшанов С.В. Измерение мгновенной частоты широкополосных сигналов на коротком интервале наблюдения // Измерительная техника. – 2008. – № 2. – С. 50.
11. Техническое описание тахометра АТТ-6002 [Электронный ресурс]. – Режим доступа: http://www.aktakom.ru/kio/index.php?SECTION_ID=504&ELEMENT_ID=7241
12. Техническое описание микросхемы ADS1602 [Электронный ресурс]. – Режим доступа: http://focus.ti.com/lit/ds/symlink/ads1602.pdf
13. Техническое описание микросхемы AD9833 [Электронный ресурс]. – Режим доступа: http://www.analog.com/static/imported-files/data_sheets/AD9833.pdf
14. Техническое описание RLC измерителя E7-8 [Электронный ресурс]. – Режим доступа: http://www.priborelektro.ru/price/E7-8.php4?deviceid=514
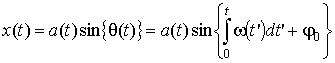 , (2)
, (2)