УДК 621.396.67
Проектирование планарной антенной решетки диапазона L1 для систем GPS/ГЛОНАСС
А. Н. Пластиков
Национальный исследовательский университет Московский энергетический институт, кафедра Антенных устройств и распространения радиоволн
Получена 31 июля 2012 г.
Аннотация. В статье рассматривается проектирование семиэлементной антенной решетки для работы в диапазоне частот L1 на основе керамических микрополосковых элементов. Численные расчеты проведены методом конечных разностей во временной области. Приводятся рекомендации по применению ручной настройки параметров разбиения модели решетки на ячейки. Отмечается различие характеристик поля излучения и коэффициента отражения одного уединенного антенного элемента и элемента в составе решетки. Описывается конструкция изготовленной антенной системы. Осуществляется сопоставление результатов численных расчетов и измерений S-параметров.
Ключевые слова: микрополосковая антенна, метод конечных разностей во временной области, метод конечного интегрирования, антенна GPS/ГЛОНАСС, антенная решетка, моделирование.
Abstract. Design of the seven element microstrip antenna array for operation in L1-band is presented in this article. Numerical calculations were made by the use of the finite difference time domain method. Advices on the application of the manual mesh settings are given. Differences between simulated characteristics of the radiation field and the reflection coefficient of a single isolated antenna element and an element in the array are noted. The construction of manufactured antenna system is described. A comparison between simulated and measured S-parameters is also presented.
Keywords: microstrip antenna, finite difference time domain method, finite integration technique, GPS/GLONASS antenna, antenna array, manual meshing.
Введение
К радиотехническим характеристикам антенн, работающих в навигационных системах GPS и ГЛОНАСС, предъявляется ряд определенных требований. Они должны обеспечивать прием/передачу волн с правой круговой поляризацией, обладать близкими к равномерным диаграммами направленности в верхнем полупространстве и обеспечивать работоспособность системы в требуемых диапазонах частот. В этой области антенной техники широкое распространение получили микрополосковые антенны [1], что связано главным образом с их планарной структурой, относительной дешевизной и простотой изготовления, высокой повторяемостью, возможностью минимизации размеров антенны за счет использования подложки с высокой величиной диэлектрической проницаемости.
Сегодня большое внимание уделяется также разработке антенных решеток (АР) для приемников сигналов систем спутниковой навигации. В частности, для ряда специфических применений [2-3] требуются антенные системы с относительно большим коэффициентом усиления с фиксированным амплитудно-фазовым распределением в раскрыве. Но наиболее широкое применение АР для приема навигационных сигналов находят в адаптивных системах помехозащиты с цифровым формированием диаграммы направленности (ДН) требуемой формы [4-5]. Данное направление актуально для объектов как военного, так и гражданского назначения. Отметим, что максимальное число помех, которые могут быть подавлены цифровой АР, на единицу меньше числа АЭ решетки [5].
Самые простые АР, предназначенные для систем адаптивной помехозащиты, включают в себя малое число элементов N≤10 и состоят из микрополосковых антенных элементов (АЭ). При этом характерные межэлементные расстояния составляют воловину длины волны и менее, что в совокупности со слабой направленностью ДН самих АЭ не позволяет пренебрегать взаимным влиянием антенн друг на друга. Вследствие этого для получения адекватной теоретической оценки радиотехнических характеристик необходимо проводить электродинамический расчет всей модели АР в целом. Близкое расположение границ АР к периферийным элементам и возможность выполнения АЭ в виде объемных планарных структур, не имеющих общей диэлектрической подложки, в свою очередь, ограничивает возможность применения численных двухмерных методов анализа плоских слоистых структур для решения таких задач.
Априори может показаться, что современные программные пакеты трехмерного электродинамического моделирования позволяют анализировать и синтезировать (с помощью параметрической оптимизации) микрополосковые АР с малым числом элементов даже не на самых современных персональных компьютерах, ведь характерные размеры таких задач не превышают нескольких длин волн. Однако на практике для анализа подобных структур могут требоваться достаточно существенные аппаратные ресурсы, а также значительные затраты машинного времени вследствие необходимости разбиения каждого из элементов решетки на достаточно большое число ячеек сетки, особенно если используемые АЭ имеют малые габариты, например, за счет использования излучателей сложной изрезанной формы и/или применения материалов с высокой диэлектрической проницаемостью.
В предлагаемой работе рассматривается проектирование семиэлементной планарной АР диапазона L1 (1574–1610 МГц), которая состоит из коммерчески доступных малогабаритных керамических АЭ и может использоваться в приемниках с адаптивными алгоритмами шумоподавления. В первой части статьи дается характеристика используемым АЭ, проводится расчет уединенного элемента и описывается схема размещения АЭ в составе решетки. Во второй части описываются результаты моделирования всей АР, осуществляется выбор материал общего диэлектрического основания и взаимного положения АЭ. Отмечается различие между собой характеристик поля излучения в дальней зоне и коэффициентов отражения для антенн в составе АР и одного уединенного АЭ. Для проведения численных расчетов использован метод конечных разностей во временной области (КРВО). Отдельное внимание уделено рекомендациям по использованию ручной настройки параметров разбиения модели решетки на ячейки. В третьей части работы приводятся результаты измерения элементов матрицы рассеяния изготовленного образца АР.
1. Описание схемы размещения элементов и их характеристика
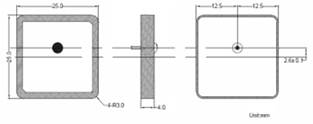
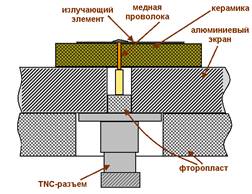
Разработка АР проводилась с использованием микрополосковых АЭ компании Amotech. Они состоят из серебряного излучающего элемента, керамической подложки и возбуждающего штыря (см. рис. 1,а). Неотъемлемой частью такой микрополосковой антенны является металлический “экран” стандартным размером 70х70 мм, не поставляемый фирмой-изготовителем вместе с данными антеннами.
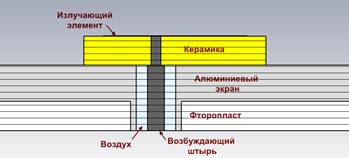
На рис. 1,б изображен профиль излучающего элемента используемых АЭ. Отметим, что круговая поляризация поля излучения микрополосковой антенны может быть достигнута в случае, когда в образуемом антенной резонаторе возбуждаются две ортогональные моды с фазовым сдвигом 90°. В нашем случае для получения поляризации поля, близкой к круговой, используется асимметрия, а именно срез двух краев квадратного элемента. Это позволяет разнести и резонансные частоты двух возбуждаемых мод. Используемая одноточечная система возбуждения достаточно проста в реализации, однако уступает двухточечной по полосе рабочих частот [6] и, зачастую, величине максимально достижимого коэффициента эллиптичности (КЭ).
|
а) |
б) |
|
Рис. 1. Микрополосковый антенный элемент компании Amotech: общий вид (а) и геометрия излучающего элемента (б)
|
|
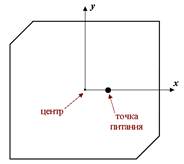
Соседние элементы разрабатываемой АР должны находиться на расстоянии половины длины волны друг от друга, которое для центральной частоты диапазона L1 составляет величину d = 93,2 мм. В центре АР находится ее центральный элемент, остальные шесть АЭ располагаются в вершинах правильного шестиугольника. На рис. 2 схематически показано расположение элементов такой решетки. Вследствие необходимости расположения центров шести периферийных АЭ на окружности радиуса d относительно центра центрального элемента размеры стороны квадратных металлических экранов выбраны равными 65 мм (вместо стандартных по документации 70 мм, при которых края соседних экранов будут пересекаться), вследствие чего, как показало компьютерное моделирование, резонансные частоты одного уединенного АЭ смещаются на несколько мегагерц в сторону больших частот.
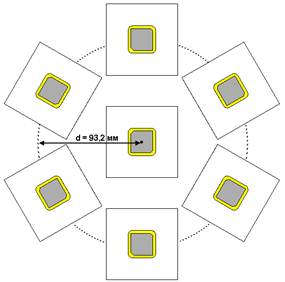
Рис. 2. Схема размещения элементов в разрабатываемой АР
2. Моделирование одного уединенного элемента
Для проверки адекватности численных расчетов и определения необходимого “качества” сетки разбиения модели (подробнее об этом см. в следующем разделе работы) было проведено моделирование одной уединенной микрополосковой антенны в среде CST Microwave Studio [7] методом конечного интегрирования во временной области [7-8], который представляет собой не что иное, как более широко известный метод конечных разностей во временной области (Finite Difference Time Domain, FDTD) [9].
Построенная модель изображена на рис. 3. Габариты металлического экрана составляют 65х65х5 мм, керамической подложки – 25х25х4 мм. Для возбуждения использовалась воздушная 50-омная коаксиальная линия, располагающаяся внутри экрана. В качестве материала излучающего элемента и возбуждающего штыря задавалось серебро, материал экрана – алюминий, параметры керамической подложки задавались следующими: диэлектрическая проницаемость ε=20,5 (среднее значение согласно спецификации на антенну) и тангенс угла диэлектрических потерь tanδ=0,002.
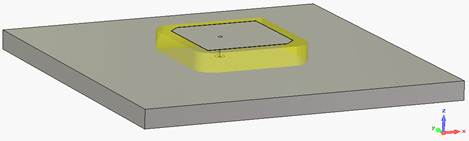
Рис. 3. Модель микрополосковой антенны
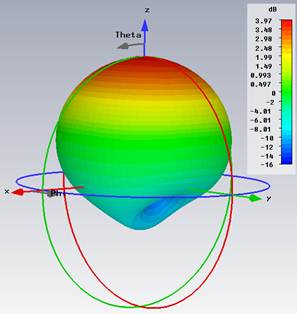
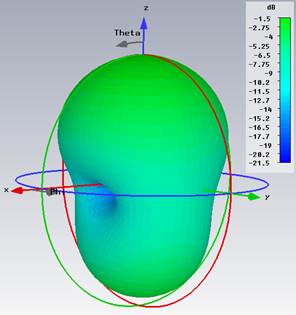
На рис. 4 приведены рассчитанные ко- (правая круговая поляризация) и кросс-поляризационные (левая круговая поляризация) диаграммы направленности АЭ. Коэффициент усиления антенны составляет около 4 дБ. Рассчитанные частотные характеристики коэффициента отражения имеют два характерных минимума и с учетом возможного разброса параметров АЭ хорошо соответствуют данным измерений (для модели с металлическим экраном габаритами 70х70), приведенным в документации на АЭ.
|
а) |
б) |
|
Рис. 4. Пространственные ДН АЭ на частоте 1,6 ГГц: ко-поляризационная (а) и кросс-поляризационная (б) составляющие |
|
3. Особенности моделирования антенной решетки
Для того чтобы снизить возможное влияние многолучевости (интерференции от металлических поверхностей) было решено располагать элементы антенной системы на общей опорной диэлектрической подложке с отсутствием металлизации с какой-либо из ее сторон.
Одним из требований, предъявляемых к проектируемой АР, была минимизация наклона фазочастотных характеристик arg(Sij) элементов матрицы рассеяния, соответствующих соседним элементам решетки, в рабочей полосе частот. Или иначе минимизация группового времени задержки коэффициентов взаимной связи Sij. Проведенные предварительные численные исследования рассматриваемой конструкции АР показали, что угол наклона фазочастотных характеристик растет при увеличении диэлектрической проницаемости опорного диэлектрика. Вследствие этого в качестве материала последнего был выбран фторопласт, диэлектрическая проницаемость которого невелика (ε=2…2,1). Толщина листа составила 5 мм.
Для получения результатов расчета матрицы S-параметров, более приближенных к реальной АР, схема возбуждения АЭ была немного модифицирована относительно использованной выше для одного уединенного элемента. Так, возбуждающий АЭ штырь, в сечении экрана являющийся центральной жилой питающей коаксиальной линии, ступенчато меняет свой радиус на границе алюминиевого экрана и керамической подложки. На рис. 5 представлена схема питания АЭ, использованная при изготовлении АР, а также сечение соответствующей области электродинамической модели. Коаксиальная линия с воздушным заполнением по-прежнему имеет волновое сопротивление 50 Ом. Отметим, что более существенное усложнение схемы возбуждения не проводилось вследствие отсутствия информации о внутреннем строении используемых TNC-разъемов. Как мы покажем далее, это, впрочем, не помешало получить достаточно хорошее соответствие между результатами расчета и измерений матрицы S-параметров.
|
а) |
б) |
|
Рис.
5. Схема питания АЭ при изготовлении (а) и использованная для
моделирования модель питания (б) |
|
Взаимное расположение элементов в составе АР также оказывает определенное влияние на интересующие нас частотные характеристики arg(Sij). В результате моделирования из нескольких возможных вариантов расположения периферийных АЭ был выбрана структура, изображенная на рис. 6. Данный вариант характеризуется максимальной удаленностью точек питания периферийных элементов от центрального АЭ и позволяет в том числе минимизировать взаимные связи |Sij| между антеннами.
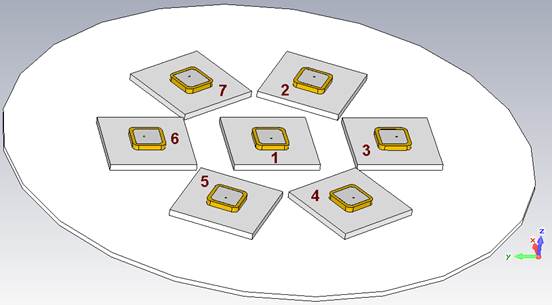
Рис. 6. Модель АР в программе Microwave Studio с используемой нумерацией антенных элементов
Остановимся на некоторых вопросах, связанных
с самим процессом моделирования. При использовании метода КРВО для
расчета
многопортового устройства (2N-полюсника) необходимо провести
N расчетов переходного
процесса распространения входного
сигнала, по одному на каждый порт. В нашем случае имеем N=7. Вследствие
этого
при использовании адаптивного алгоритма разбиения электродинамической
модели на
ячейки, подразумевающего проведение нескольких шагов итерационной
процедуры
уплотнения сетки разбиения, затраты времени на расчет рассматриваемой
АР могут
быть существенными. Для сокращения времени, необходимого для расчета
решетки,
была использована возможность задания параметров разбиения модели
вручную.
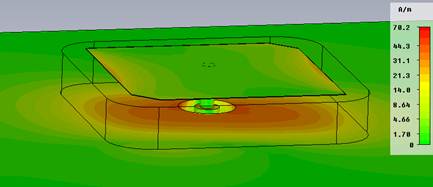
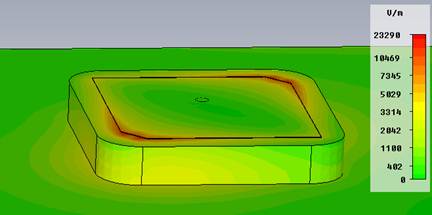
Наибольшая плотность энергии электромагнитного поля АЭ наблюдается в пространстве между излучающим элементов и экраном, а также вблизи кромок излучающего элемента (см. рис. 7). Следовательно, именно вблизи этих областей и требуется в первую очередь уплотнить сетку разбиения модели относительно некоего грубого исходного разбиения. Кроме того, для получения более точного результата расчета матрицы S-параметров требуется также уплотнить сетку внутри коаксиальной линии питания. На рис. 8 изображена использованная сетка разбиения для всей модели в плоскости решетки. Общее число элементов разбиения – прямоугольных параллелепипедов составило более 1,2 миллиона. Предварительную проверку “качества” полученной сетки можно осуществить на примере расчета одного уединенного АЭ.
|
а) |
|
б) |
|
Рис. 7. Усредненные за период рассчитанные распределения поверхностных токов (а) и вектора электрического поля (б) для одного уединенного АЭ при подаче на его вход мощности 1 Вт |
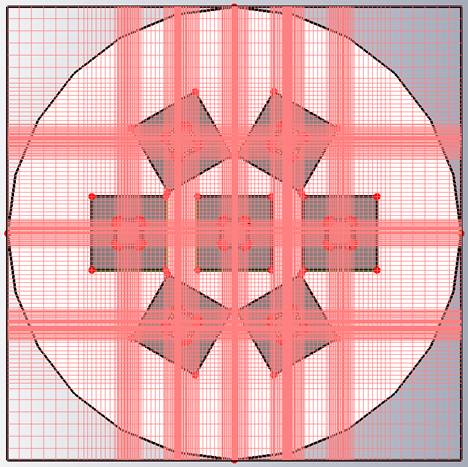
Рис. 8. Разбиение на ячейки модели АР
Отметим также следующую особенность используемого численного метода расчета. Недостаток классического метода КРВО в трехмерном пространстве с использованием декартовых ортогональных сеток (рис. 9,а) состоит в отсутствии "гибкости", когда требуется дискретизировать сложные изогнутые структуры. В результате реальная структура вдоль искривленных границ аппроксимируется ортогональными элементами – прямоугольными параллелепипедами и для повышения точности расчета может потребоваться сделать шаг сетки разбиения вдоль этих границ очень малым. Однако наличие в сетке элемента разбиения с излишне малыми размерами по сравнению с длиной волны неизбежно приведет к росту времени расчета, т.к. для сохранения стабильности вычислений потребуется уменьшить шаг расчета временного процесса [9]. При этом к тому же возрастает и численная сложность задачи вследствие роста числа самих элементов разбиения.
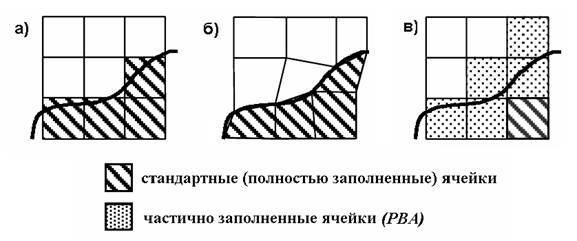
Рис. 9. Сеточная аппроксимация искривленных границ в методе КРВО: стандартная (а), с использованием неортогональной сетки (б) и PBA (в)
Наиболее общий подход к учету искривленных границ состоит в использовании обобщенных конформных неортогональных сеток (рис. 9,б). Но применение неортогонального алгоритма иногда ограничивается ростом числовой сложности задачи и необходимостью создания облегающей границы структурированной неортогональной сетки.
В качестве более эффективного подхода была предложена техника идеальной аппроксимации границы (Perfect Boundary Approximation, PBA) [10]. При этом подходе нет необходимости согласовывать ортогональную расчетную сетку со скругленными границами (рис. 9,в). Вместо этого учитывается дополнительная информация о содержимом ячеек пространства, что приводит к алгоритму второго порядка точности для границ произвольной формы. При расчетах рассматриваемой АР в программе Microwave Studio принудительно задавалась опция использования техники идеальной аппроксимации границы PBA, что позволило достаточно точно учесть наличие в модели решетки элементов геометрии, грани которых искривлены или не совпадают с направлениями осей декартовой системы координат, а также принять во внимание конечную толщину металлического слоя излучающих элементов.
Таким образом при задании адекватных параметров разбиения, учитывающих особенности структуры электромагнитного поля в устройстве и особенности самого численного метода КРВО, можно сократить время анализа модели того или иного устройства по сравнению со случаем использования адаптивного уплотнения сетки при сохранении сопоставимого уровня точности расчетов. В среде Microwave Studio использовать аналогичный подход к проектированию можно и при решении задач методом конечного интегрирования в частотной области, также использующим ортогональную сетку разбиения. Подобный подход видится особенно эффективным на стадии оптимизации модели устройства.
Опыт моделирования микрополосковых антенн круговой поляризации показывает, что такая рассчитываемая характеристика антенны, как коэффициент эллиптичности, зачастую более чувствительна к точности сетки разбиения по сравнению с матрицей S-параметров и ДН. Поэтому для того, чтобы быть полностью уверенным в точности полученных результатов, окончательную (оптимизированную) модель устройства все же следует рассчитать с использованием более мелкой сетки разбиения, параметры которой установлены вручную, или автоматического адаптивного алгоритма разбиения.
4. Результаты моделирования
Рассмотрим результаты проведенного электродинамического моделирования. На рис. 10 изображена рассчитанная временная зависимость переходного процесса при возбуждении первого порта АР. На рисунках 11 и 12 представлены рассчитанные частотные зависимости модулей и аргументов элементов первой строки матрицы S-параметров решетки в рабочем диапазоне частот. Заметим, что для уменьшения времени анализа модели решетки методом КРВО расчет был проведен в полосе частот, в несколько раз более широкой по сравнению с шириной рабочего диапазона L1 (1574–1610 МГц).
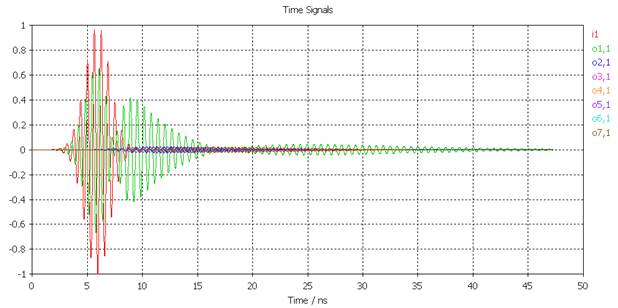
Рис. 10. Поданный на вход центрального элемента сигнал (i1) и сигналы, отраженные от входов всех АЭ
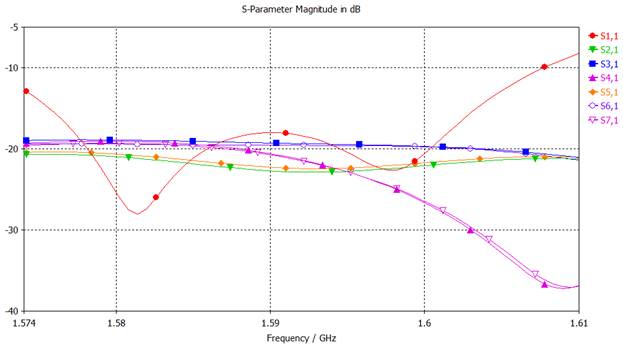
Рис. 11. Рассчитанные модули элементов 1-й строки матрицы S-параметров
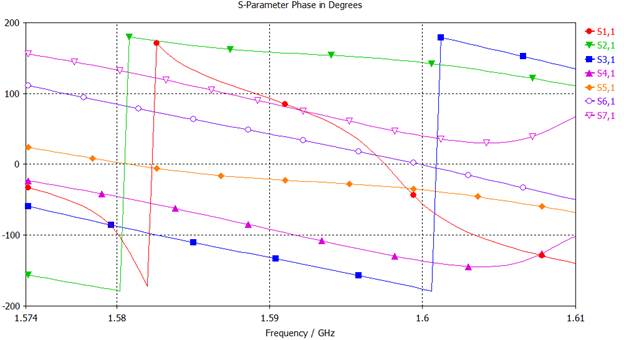
Рис. 12. Рассчитанные аргументы элементов 1-й строки матрицы S-параметров
Сравним рассчитанные характеристики коэффициентов отражения и полей излучения одного уединенного АЭ и двух АЭ в составе АР. На рис. 13 приведены частотные зависимости коэффициентов отражения. Сопоставление графиков показывает, что полоса частот центрального АЭ по уровню модуля коэффициента отражения -10 дБ более узка по сравнению с полосой уединенного АЭ. Полоса частот периферийного элемента сопоставима с полосой уединенного, но сдвинута в область более низких частот и характеризуется “заплыванием” первого минимума коэффициента отражения.
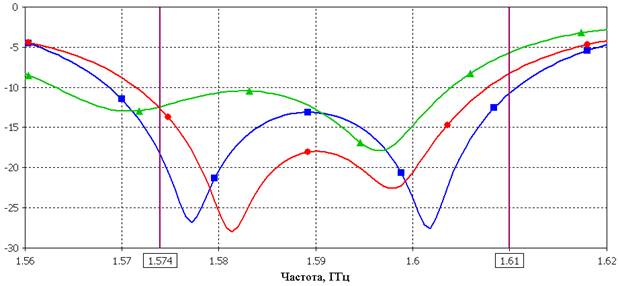
Рис. 13. Коэффициенты отражения одного уединенного АЭ и двух отдельных АЭ в составе АР (в дБ):

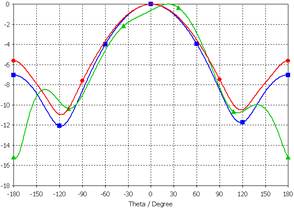
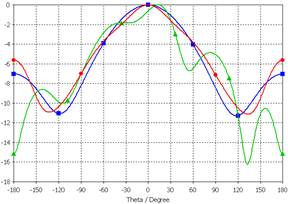
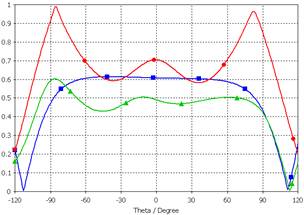
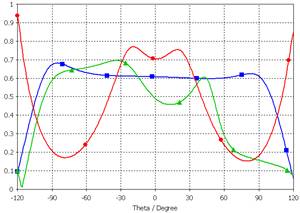
Графики, изображенные на рисунках 14 и 15, показывают видоизменение ДН и КЭ при переходе от одного уединенного АЭ к элементам в составе решетки. Видно, что в двух представленных плоскостях ДН центрального элемента отличается от ДН уединенного АЭ несущественно, в то же время ДН периферийного элемента решетки является несимметричной и “изрезанной”. Графики КЭ различаются в большей степени. Отметим существенное различие КЭ в двух ортогональных плоскостях для центрального АЭ: в направлениях, близких к скользящим углам θ=±90°, в плоскости, проходящей через точку питания, КЭ близок к 1, в то время как в перпендикулярной плоскости КЭ снижается до уровня 0,2.
|
|
|
|
а) |
б) |
Рис. 14. Нормированные ДН одного уединенного АЭ и двух отдельных АЭ в составе АР в плоскости расположения точки питания (а) и ортогональной ей плоскости (б) в логарифмическом масштабе:

|
|
|
|
а) |
б) |
Рис. 15. КЭ одного уединенного АЭ и двух отдельных АЭ в составе АР в плоскости расположения точки питания (а) и ортогональной ей плоскости (б):

Таким
образом ДН элементов в составе рассматриваемой АР
отличаются друг от друга. Знание характеристик поля излучения всех
элементов может
быть положено в основу расчета комплексного вектора весовых
коэффициентов (ВВК)
для формирования требуемой ДН всей решетки, например, для синтеза
провала в
направлении прихода помеховых сигналов при наличии априорной информации
об
угловых координатах целей и помех.
В случаях, когда направление прихода помехи неизвестно, широкое распространение получили подходы построения адаптивных алгоритмов, в основе которых лежит поэлементный принцип поиска оптимального ВВК по критериям минимизации отношения сигнал-шум или другого целевого функционала. К недостаткам подобных методов относятся минимальное использование априорной информации о структуре АР, а также резкое увеличение вычислительной сложности алгоритмов с ростом числа АЭ.
Отмеченных недостатков лишен так называемый метод “групповой” адаптации [11], суть которого состоит в последовательном сканировании провалами в заранее определенных направлениях ДН (например, в направлении боковых лепестков) с помощью метода апертурных ортогональных полиномов [12], посредством которого можно синтезировать требуемое распределение ВВК сразу на всем раскрыве АР. В этом случае важно знать ДН каждого элемента решетки. Однако актуальность подобного подхода для случая АР с малым числом элементов N (в нашем случае N=7) небесспорна.
5. Изготовленная антенная решетка. Сопоставление измерений и численных расчетов
На рис. 16 приведена фотография АР, изготовленной в соответствии с отмеченными выше конструктивными особенностями. Вследствие отсутствия на момент проведения измерений технической базы, необходимой для определения характеристик поля излучения АР в дальней зоне, испытания ограничились измерением элементов матрицы S-параметров. Соответствующие измерения проводились с помощью векторного анализатора цепей Rohde & Schwarz ZVB4, при этом сама АР помещалась в безэховую камеру.

Рис. 16. Фотография изготовленной АР
Ниже приведены результаты измерений S-параметров: на рис. 17 – частотные зависимости модулей нескольких диагональных элементов матрицы рассеяния (в дБ), на рис. 18 и 19 – частотные характеристики модулей (в дБ) и аргументов S-параметров (в градусах), характеризующих взаимные связи между элементами АР. Эти зависимости позволяют заключить, что в диапазоне рабочих частот уровни взаимных связей (выражаемые модулями S-параметров) составляют менее минус 17дБ. Соответствующие разности уровней фазочастотных характеристик на границах диапазона L1 составляют в среднем около 180 градусов (см. рис. 19), что соответствует линейной зависимости с углом наклона 5 градусов на мегагерц.
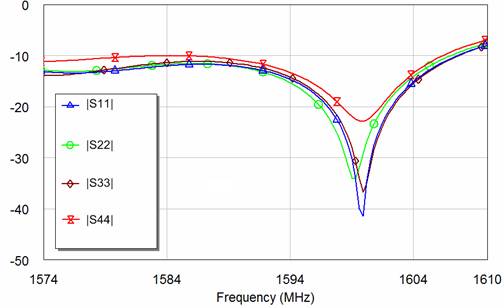
Рис. 17. Измеренные модули диагональных элементов матрицы S-параметров
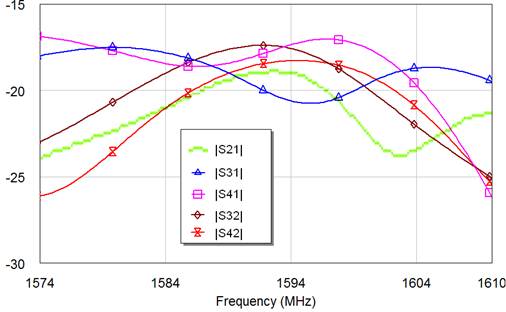
Рис. 18. Измеренные модули коэффициентов взаимной связи между АЭ
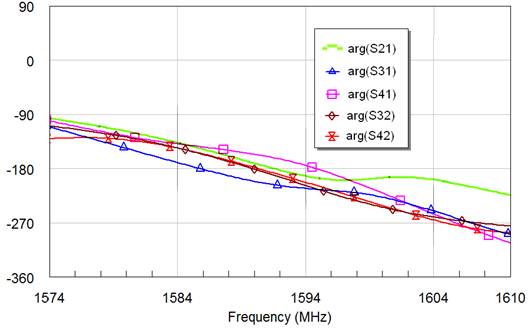
Рис. 19. Измеренные аргументы коэффициентов взаимной связи между АЭ
Осуществим сопоставление результатов, полученных при моделировании, и измерений. На рис. 20 и 21 представлены соответствующие зависимости модулей и аргументов S-параметров; при этом результаты моделирования отображены сплошными кривыми, а результаты измерений – полыми символами. Отметим, что для адекватного измерения/вычисления уровней аргументов S-параметров необходимо проводить отсчет фаз относительно точек положения фазовых центров (центров излучения) антенных элементов (что не принято во внимание в результатах моделирования, приведенных на рис. 12).
Вследствие разнесения соседних антенных элементов на половину длины волны, соответствующей центральной частоте f0 = 1592 МГц диапазона L1, на частоте f0 следует ожидать разности фаз S-параметров, соответствующих соседним элементам, около 180 градусов. Отметим, что это было учтено при обработке результатов измерений, приведенных на рис. 19, где для наглядного сравнения наклона графиков аналогичным образом была смещена кривая, соответствующая аргументу S42. На графиках рис. 21 учет отмеченного факта проведен и для результатов моделирования, что позволяет провести адекватное сравнение расчетов и измерений аргументов S-параметров.
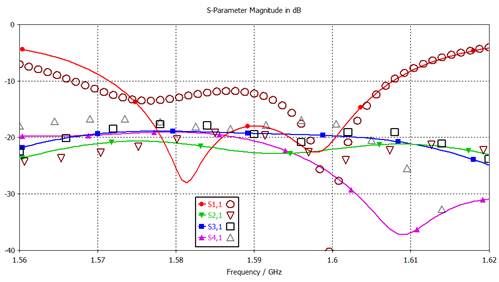
Рис. 20. Сопоставление модулей S-параметров:
сплошные кривые – численные расчеты, полые символы – измерения
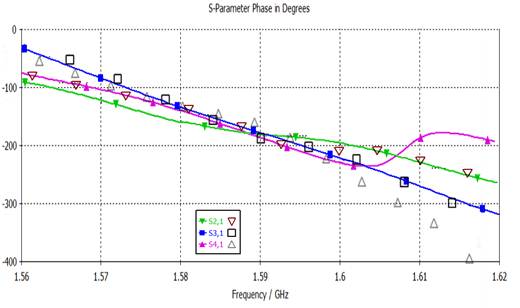
Рис. 21. Сопоставление аргументов S-параметров:
сплошные кривые – численные расчеты, полые символы – измерения
Достаточно существенные отличия наблюдаются между кривыми, соответствующими модулям коэффициента S11, а также модулям и аргументам коэффициента S41. Однако к причинам возникновения этих различий можно отнести погрешности изготовления АР, возможный разброс параметров используемых керамических микрополосковых антенн, а также то, что при моделировании не учитывались разъемы TNC и переходники TNC-SMA, используемые при измерениях. Все это в большей мере должно влиять на диагональные элементы S-матрицы, характеризующие степень согласования АЭ с линией питания. Так, представленные результаты расчетов и измерений, соответствующие параметрам S21 и S31, достаточно хорошо согласуются друг с другом. Не очень хорошее соответствие же в зависимостях модуля и аргумента S41, по всей видимости, связано с недостаточно большой точностью изготовления 4-го АЭ, что также повлияло и на ухудшение параметра |S44| (см. рис. 17).
Заключение
В статье был рассмотрен процесс проектирования семиэлементной АР диапазона L1, которая может использоваться в приемниках навигационных систем GPS/ГЛОНАСС с адаптивными алгоритмами подавления помех. Отмечены конструктивные особенности изготовленного образца АР. Выбран материал общего диэлектрического основания и взаимное положение АЭ, позволяющие минимизировать наклон частотных зависимостей аргументов arg(Sij) элементов матрицы рассеяния, характеризующих взаимные связи между соседними элементами.
Отмечено различие между собой характеристик поля излучения в дальней зоне и коэффициентов матрицы рассеяния для антенн в составе АР и одного уединенного АЭ. Численные расчеты проведены методом КРВО. Отдельное внимание уделено процессу ручного разбиения модели АР на ячейки, отмечены характерные особенности самого численного метода КРВО. Результаты численных расчетов элементов матрицы S-параметров достаточно хорошо согласуются с результатами измерений.
Автор выражает благодарность к.т.н. А.Ю. Шатилову за поставленную задачу и помощь в сборке образца антенной решетки, а также А.И. Буданевичу за проведение измерений.
Литература
1. Лось В. Ф. Микрополосковые и диэлектрические резонаторные антенны. САПР-модели: методы математического моделирования. — ИПРЖР: 2002.
2. Ксендзук А.В. "Синтез апертуры с использованием навигационной системы ГЛОНАСС" // Успехи современной радиоэлектроники, 2003, №11, с. 44-54.
3. Жексенов М.А., Печурин В.А., Волченков А.C. "Антенная решетка с печатными излучателями для БПЛА" // Труды МАИ, 2011, вып. № 45.
4. Ю.С. Яскин, В.Н. Харисов, В.С. Ефименко, С.Н. Бойко, С.Г. Быстраков, А.В. Пастухов, С.А. Савельев, "Характеристики подавления помех в первом образце помехоустойчивой аппаратуры потребителей СРНС ГЛОНАСС/GPS с адаптивной антенной решеткой" // Радиотехника, 2010, №7, с. 127-136.
5. В.И. Слюсар, "Цифровые антенные решетки: решения задач GPS" // ЭЛЕКТРОНИКА: НТБ, 2009, №1, стр. 74-78.
6. Thomas A. Milligan. Modern antenna design. – Wiley-IEEE Press, 2005.
7. Курушин А.А., Пластиков А.Н. Студия проектирования СВЧ устройств Microwave Studio. Книга для студентов и исследователей – М.: Издательство МЭИ, 2012.
8. M. Clemens and T. Weiland, “DISCRETE ELECTROMAGNETISM WITH THE FINITE INTEGRATION TECHNIQUE” // Progress In Electromagnetics Research, 2001, PIER 32, p. 65–87.
9. K. S. Yee, "Numerical solution of initial boundary value problems involving Maxwell's equations in isotropic media" // IEEE Trans. on Antennas Propagat., 1996, vol. 14, no. 4, p. 302-307.
10. B. Krietenstein, R. Schumann, P. Thoma, T.Weiland: “The Perfect Boundary Approximation Technique Facing the big Challenge of High Precision Field Computation”, Proc. Of the Int. Linear Accelerator Conference, Chicago, USA, 1998, p. 860-862
11. Гнедак П.В. Фазовый синтез нулей в диаграммах направленности апертурных антенн на основе метода апертурных ортогональных полиномов: Автореф. дис. ... канд. техн. наук. - М., 2009.
12. Гусевский В.И. "Метод апертурных ортогональных полиномов и его применение в антенной технике" // Успехи современной радиоэлектроники, 2001, № 3, с. 50-72.