“ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ” N 8, 2012

оглавление

УДК 517.946:681.3                          

Метод расчета электромагнитного поля в задачах микроэлектроники

 

И. А. Конников

Получена 8 июня 2012 г., после доработки – 31 июля 2012 г.

 

Аннотация. Предлагается метод расчёта электромагнитного поля, описываемого волновым уравнением, учитывающий особенности радиоэлектроники и ориентированный на оценку перекрёстных наводок в коммуникационных проводниках радиоэлектронных модулей. Метод основан на использовании эквивалентной постоянной распространения и позволяет снизить объём вычислений по сравнению с другими методами, основанными на строго динамическом подходе и использующими пространственную дискретизацию моделируемого объекта или интеграл Зоммерфельда. Проводится оценка области корректного использования метода.

Ключевые слова: эквивалентная постоянная распространения, перекрёстные наводки, расчёт поля.

Abstract. A method of computation of the electromagnetic field described with the wave equation is offered with respect to the peculiarities of radio electronics. The method is based upon the employment of the equivalent propagation constant and is oriented at the estimation of crosstalk in the conductors of radio electronic units. It enables to diminish the amount of computation if compared to other techniques based upon the strict dynamical approach and employing the spatial discretization of the object simulated or the Sommerfeld integral. The applicability domain of the method is assessed.

Keywords: equivalent propagation constant, crosstalk, field computation.

 

Введение

          Оценка паразитных электромагнитных эффектов (ПЭМЭ) в радиоэлектронных модулях – актуальная наукоёмкая задача, требующая соответствующего научно-методического обеспечения. Получить удовлетворительное решение этой задачи возможно лишь при разработке изделий радиоэлектроники средствами комплексной САПР на основе маршрута проектирования, который был предложен в [1]. Он предполагает экстракцию эквивалентной электрической схемы проектируемого модуля, которая, помимо элементов принципиальной схемы, включает элементы, моделирующие ПЭМЭ. Экстракция проводится в автоматическом режиме. Для оценки влияния ПЭМЭ проводится расчёт выходных электрических характеристик средствами подсистемы схемотехнического проектирования. Недостаток такого подхода – слишком высокая размерность решаемой задачи, неадекватная возможностям современных вычислительных средств широко доступного класса. Имеется настоятельная необходимость снижения вычислительной ёмкости используемого решения.

Известные решения

          Решение задачи учёта влияния ПЭМЭ проводится или на основе прямых расчётов электромагнитного поля, или на основе использования схем замещения, включающих частотонезависимые активные сопротивления, ёмкости и индуктивности. Однако при использовании таких схем замещения погрешность моделирования ПЭМЭ имеет две составляющие. Во-первых, это – погрешность за счёт использования для моделирования поля реактивностей, которые рассчитываются через статическую составляющую поля, превалирующую в ближней зоне, но быстро убывающую с расстоянием. Моделирование наводок через взаимные ёмкости и индуктивности (в классичекой трактовке этих понятий) принципиально не учитывает полe излучения и полe переходной зоны. Это может привести к недопустимо высокой погрешности при проектировании устройств субнаносекундного диапазона, поэтому паразитные ёмкости и индуктивности целесообразно использовать только для моделирования распространения поля вдоль коммутационных проводников (для расчёта времени задержки, волнового сопротивления и т.п.). Для моделирования взаимного влияния проводников следует использовать иные математические модели, учитывающие все составляющие поля, в том числе поле излучения. Во-вторых, это – погрешность, обусловленная пространственной дискретизацией системы с распределёнными параметрами, состоящей из объекта – источника помехи, объекта – приёмника помехи и канала распространения электромагнитной энергии. Эта дискретизация неминуемо приводит к использованию цепочечных схем замещения, причём для обеспечения приемлемой точности степень дискретизации и число звеньев цепочечных эквивалентных схем приходится увеличивать настолько, что размерность задачи становится недопустимо большой. Промежуточное положение занимает известный метод, основанный на использовании теории связанных линий с распределёнными параметрами. Этот метод не предполагает пространственную дискретизацию моделируемого объекта, имеет относительно небольшую вычислительную ёмкость[1], однако электромагнитная связь линий моделируется также через взаимные ёмкость и индуктивность, что принципиально и неизбежно ограничивает область корректного использования метода по частотному диапазону. По-видимому, продолжение попыток решать проблему оценки наводимых помех прежними методами (через расчёт взаимных емкостей и индуктивностей в классической трактовке этих понятий, с использованием пространственной дискретизации или без неё) для решения проектных задач большой размерности бесперспективно.

          Приемлемое решение необходимо искать на пути прямого использования методов теории электромагнитного поля, органично учитывающих распределённый характер конструктива и позволяющих построить модели, область корректного использования которых не ограничена ближней зоной. В этом случае наводимая помеха может моделироваться генераторами напряжения и/или тока (как это делается например, в [2] и др.), или же при помощи специальной эквивалентной схемы (например, такой, как предлагаемая в [3]). Как ЭДС такого генератора, так и параметры элементов эквивалентной схемы следует рассчитывать по формулам, которые должны быть получены с помощью интегрирования всех составляющих (а не только статической составляющей) электромагнитного поля источника помехи по его объёму, как в [3]. При таком подходе индуцированная ЭДС и значения параметров являются интегральными характеристиками системы, состоящей из источника, рецептора помехи и канала паразитной связи. Для количественной оценки помехи пространственная дискретизация такой системы совершенно не обязательна. Однако, хорошо известные методы расчёта поля, использующие пространственную дискретизацию моделируемого объекта на мелкой сетке (метод граничных элементов, метод моментов и др.) совершенно непригодны для реализации описанного в [1] маршрута проектирования вследствие непомерно высоких затрат машинного времени. Тем же недостатком обладает и метод функции Грина, предполагающий использование интеграла Зоммерфельда – строгого аналитического решения волнового уравнения на частоте w>0 для электромагнитного поля в слоистой среде. Необходим иной подход, учитывающий особенности радиоэлектроники.

Специфика расчёта поля в радиоэлектронике

          Проблема моделирования электронных модулей с учётом паразитных наводок (помех)  имеет свою специфику, определяющую задачи и методы исследования, форму представления результатов, методы их реализации и использования. При решении названной проблемы основной акцент должен быть сделан не на изучение условий приёмопередачи, как требуется в радиотехнике, а на количественную оценку напряжений или токов помехи от конкретного источника. Важной особенностью этой проблемы является существенно большее, чем в радиотехнике, количество источников и приёмников поля, учитываемых при анализе, что проявляется в более высокой размерности подлежащих решению частных задач радиоэлектроники. Слоистые среды радиоэлектроники отличаются более правильной формой границ раздела слоёв и имеют другие электрофизические свойства слоёв по сравнению с естественной средой распространения радиоволн, что часто не позволяет вводить используемые в радиотехнике допущения. В то же время свойства используемых в радиоэлектронике изоляционных материалов нередко позволяют пренебречь активной проводимостью канала распространения электромагнитной энергииfhf, что значительно упрощает расчёт поля. С другой стороны, расстояния и размеры объектов радиоэлектроники (особенно микроэлектроники) принципиально меньше, чем расстояния и размеры объектов радиотехники и поэтому характеризуются меньшей электрической длиной. Следовательно, квазистационарное приближение при разработке математических методов, моделей, алгоритмов, расчёте помех и анализе электромагнитной совместимости, вообще говоря, является в радиоэлектронике более корректным, и это является главным методическим отличием решения задач радиоэлектроники от задач радиотехники, сходных по постановке и характеру электромагнитных процессов. В частности, важнейшей особенностью слоистых сред радиоэлектроники являются их малые по сравнению с длиной волны поперечные размеры, поэтому математическое моделирование слоистости среды при расчёте поля в микросхемах и на печатных платах вполне допустимо и целесообразно проводить в квазистационарном приближении, считая слои тонкими. Такое приближение должно существенно упростить как процесс разработки математических методов, моделей и алгоритмов, так и само математическое обеспечение, а также снизить затраты  машинного  времени на моделирование.

Предлагаемый метод

          В данной работе поставленную задачу предлагается решать, сочетая использование методов математической физики и электротехники, адаптированных к специфике радиоэлектронных модулей нулевого и первого уровней. Решение ориентировано на проектные задачи большой размерности с максимальным использованием аналитических методов, реализуемых заранее при разработке соответствующего математического и программного обеспечения, в отличие от ориентации на численные методы, предполагающие проведение основного, причём гораздо большего, объёма вычислений в процессе моделирования.

          Вычислительную ёмкость задач можно значительно снизить, если использовать электродинамический подход на основе метода эквивалентной постоянной распространения (ЭПР), предложенный в [4]. В этом случае функция Грина , которая является решением волнового уравнения, для слоистой среды описывается выражением того же вида, что и для однородной среды:

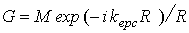,                                         (1)

где   M   –  амплитудный  множитель;    – ЭПР; R – радиус в сферической системе координат; константа Кулона ; константа Био-Савара ;  и  – эквивалентные относительные диэлектрическая и магнитная проницаемости слоистой среды, соответственно;  – угловая частота; p  = 3.14159....

          Выражение (1) может использоваться не только для описания распространения поля в азимутальном направлении, но и перпендикулярно границам раздела слоёв. Поле в слое, где расположен источник помехи, определяется, в основном, физическими характеристиками этого слоя; поле вблизи границы раздела определяется, в основном, физическими характеристиками слоёв, прилегающих к границе раздела. Влияние остальных слоёв существенно ниже, особенно на малых азимутальных расстояниях r, характерных для микроэлектроники. Поэтому влияние неприлегающих слоёв можно смоделировать в квазистационарном приближении, считая слои тонкими. Значения  и  целесообразно рассчитывать по единым для каждого слоя среды более простым формулам, отличным от предлагаемых в [4]:

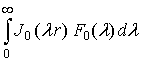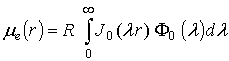/;    ,                 (2)

 

где  – полученная при решении электростатической задачи математическая модель слоистой среды, которая соответствует конструкции электронного модуля [5];  – полученная при решении магнитостатической задачи математическая модель той же среды; – функция Бесселя первого рода нулевого порядка; x, y, z  – абсцисса, ордината и аппликата точки, где вычисляется поле; x0, y0, z0 – абсцисса, ордината и аппликата точки, где расположен элементарный источник поля;  – расстояние между источником поля и точкой, где вычисляется поле;  несобственные интегралы вычисляются по методике, описанной в [6].

          При таком определении величин  и  они не зависят от размеров и формы источника поля, что существенно снижает требуемый объём вычислений.

Частотные характеристики предлагаемой математической модели

          Идея описания электромагнитного процесса динамической математической моделью, один из параметров которой рассчитывается в квазистационарном приближении, не нова. Этот приём был использован, например, для описания электромагнитных процессов в линиях с распределёнными параметрами с помощью уравнения Гельмгольца [9]. Решение этого уравнения хорошо известно. Оно описывает распространение падающей и отражённой волн в канале распространения электромагнитной энергии, включающем проводник, и представляет собой сумму двух слагаемых с экспоненциальной зависимостью от расстояния. Показатели экспонент отличаются знаком и вычисляются через распределённые параметры линии, в том числе – через ёмкость и индуктивность, которые рассчитываются на основе решения уравнений Лапласа для потенциалов электрического и магнитного полей, т.е., строго говоря, на постоянном токе. Тем не менее, полученная математическая модель эффективно используется в весьма широком диапазоне частот. На этой основе была построена мощная теория, известная как теория линий с распределёнными параметрами, область корректного применения которой весьма обширна и давно известна. Корректность использования указанного приёма для описания аналогичных процессов в канале распространения электромагнитной энергии, не содержащем проводник, обсуждалась в [7]. Рассмотрим точностные характеристики математической модели (1) более подробно, проведя оценку степени её адекватности на примере задачи, допускающей строгое решение. В качестве таковой целесообразно принять задачу расчёта поля, создаваемого горизонтальным диполем вблизи плоской границы раздела двух гомогенных изотропных полупространств с постоянными распространения  и , для которой также известно строгое решение. Именно через поле горизонтального диполя вычисляются помехи в коммутационных проводниках микросхем и печатных плат. Кроме того, именно поле горизонтального источника на плоской границе полупространств является главной (т.е. наиболее весомой) составляющей поля в слоистой среде, особенно на малых расстояниях, характерных для микроэлектроники [8]. Как известно [9,с.458], решение волнового уравнения для горизонтальной компоненты вектор-потенциала поля горизонтального диполя в такой структуре может быть описано формулой Ван-дер-Поля

,

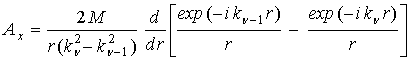которую, взяв производную, можно представить в виде:


.

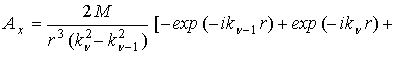
         Выделив модуль и аргумент, это выражение можно представить в виде

,

где главное значение аргумента ,

,

,

а модуль

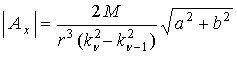.                                      (3)

          В соответствии с методом ЭПР поле на плоской границе полупространств описывается выражением

,                                          (4)

где фаза ,   .

 

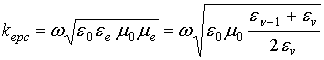         Представляет особый интерес частотная зависимость модуля и аргумента (фазы) вектор-потенциала на нижних частотах. Как показывает анализ формул (3) и (4), функция (w), точно описывающая частотную зависимость аргумента, и её производная особенностей не имеют, с изменением частоты значение аргумента  изменяется на нижних частотах квазилинейно, а аргумент  изменяется линейно во всём диапазоне частот, причём  и . При  модуль  и в пределе совпадает со значением, которое является точным решением уравнения Лапласа. Следовательно, при  погрешность моделирования модуля стремится к нулю, т.е. точность метода ЭПР растёт с уменьшением расстояния до диполя, что также подтверждается вычислительным экспериментом, часть результатов которого представлена на рисунках 1, 2 и 3. Представленные на этих рисунках зависимости являются типичными.

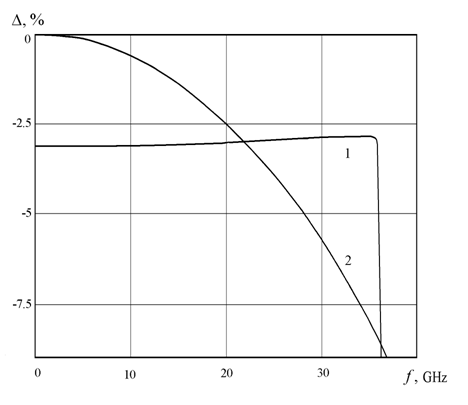
Рис. 1. Частотная зависимость относительной погрешности моделирования аргумента (кривая 1) и модуля (кривая 2) векторного потенциала на расстоянии  r=1 mm от диполя при e2=8.5.

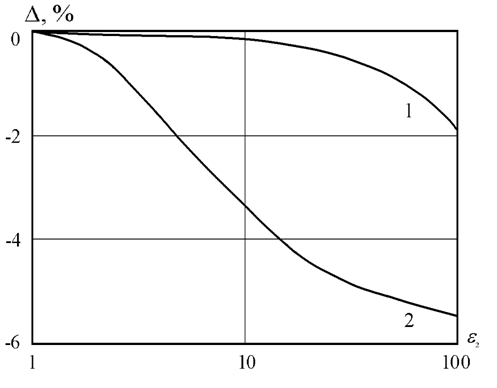
Рис. 2. Зависимость относительной погрешности моделирования модуля (кривая 1) и аргумента (кривая 2) векторного потенциала от относительной диэлектрической   проницаемости   подстилающего   слоя  на   расстоянии от диполя r = 2 mm на частоте f=2 GHz.

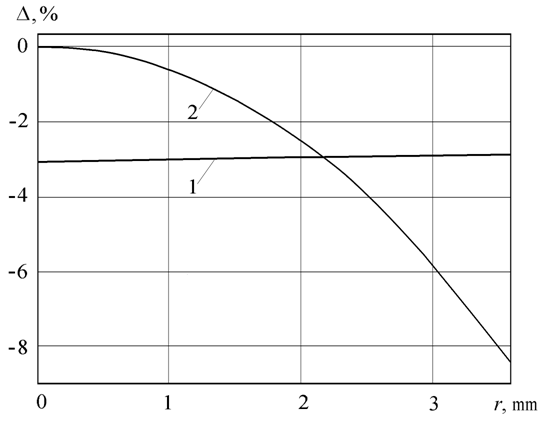
Рис. 3. Зависимость относительной погрешности моделирования аргумента (кривая 1) и модуля (кривая 2) векторного потенциала от расстояния до диполя r при e2=8.5 на частоте f=10 GHц.

 

         При проведении эксперимента погрешность вычисления модуля рассчитывалась по формуле 100(1-), %; погрешность вычисления аргумента также рассчитывалась в процентах по формуле 100(1-), %. Для снижения влияния погрешности округления вычисления проводились с учётом 32 десятичных знаков мантиссы каждого операнда.

         Анализ и обобщение результатов вычислительного эксперимента по исследованию частотной зависимости погрешности моделирования позволяют сделать следующие выводы.

          Относительные погрешности моделирования модуля и фазы вектор-потенциала  поля  отрицательны  и  возрастают  по  абсолютной  величине  с увеличением расстояния до диполя и относительной диэлектрической проницаемости подстилающего слоя. Как показали исследования, проведённые при самых различных сочетаниях параметров для частот относительной диэлектрической проницаемости платы (подложки) , расстояний ,  относительная погрешность моделирования модуля от нулевого значения на постоянном токе монотонно возрастает по абсолютной величине с увеличением частоты вплоть до частоты, при которой обеспечивается набег фазы не менее чем p/2 (см. рис.1); затем эта погрешность, оставаясь ограниченной, изменяется немонотонно, проходя через ноль и меняя знак. Частотная зависимость относительной погрешности моделирования фазы в области нижних частот, строго говоря, немонотонна, хотя с ошибкой в несколько десятых долей процента эту погрешность можно считать постоянной (не зависящей от частоты) вплоть до частоты, при которой обеспечивается набег фазы . До указанной частоты эта погрешность составляет единицы процентов и при дальнейшем увеличении частоты происходит быстрое увеличение относительной погрешности моделирования фазы по абсолютной величине. Однако, оставаясь ограниченной, эта погрешность с ростом частоты изменяется также немонотонно, проходя через ноль и меняя знак.

         Рабочая область метода ЭПР

         С формальной точки зрения рабочая область метода ЭПР снизу ограничена частотой f=0, т.е. практически не ограничена. Чтобы оценить рабочую область метода по частотному диапазону сверху, её можно ограничить частотой, при которой ошибка моделирования модуля не превосходит уровня 8-10%. Опираясь на результаты описанного выше вычислительного эксперимента, можно утверждать, что этот уровень соответствует набегу фазы не менее чем  (как известно, квазистационарное приближение соответствует соотношению )[2]. Сформированная таким образом рабочая область при самых различных сочетаниях параметров соответствует монотонному участку изменения ошибки моделирования, который предшествует участку быстрого увеличения относительной погрешности по абсолютной величине. Учитывая, что в рабочей области  (с погрешностью в несколько десятых долей процента), можно полагать, что рабочая область ограничивается, как минимум, частотой fx, при которой набег фазы  равен p/2. Записав это условие с использованием формулы (4) и решив соответствующее уравнение, получим для  верхней граничной частоты рабочей области метода ЭПР оценку снизу:

.

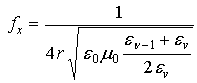         Значение fx находится далеко за пределами области квазистационарного приближения. Более того, это значение позволяет оценить верхнюю граничную частоту рабочей области метода сo значительным запасом, поскольку на более высоких частотах f>fx погрешности изменяются немонотонно, проходя через ноль и меняя знак. На рис. 4 показана зависимость верхней граничной частоты рабочей области метода ЭПР от расстояния для различных подстилающих материалов, причём имеется ввиду оценка снизу по главной составляющей поля. Из рис. 4 видно, что рабочая область метода ЭПР, даже будучи сформированной на основе нижней оценки верхней граничной частоты,  покрывает  практически  весь  диапазон  частот  и электрофизических параметров немагнитных материалов печатных плат и, тем более, микросхем и микросборок различного функционального назначения (за исключением, возможно,  имеющих  особую  специфику  радиоэлектронных  конструктивов, предназначенных для работы в области СВЧ) и включает импульсные схемы осваиваемого ныне субнаносекундного диапазона.

                          

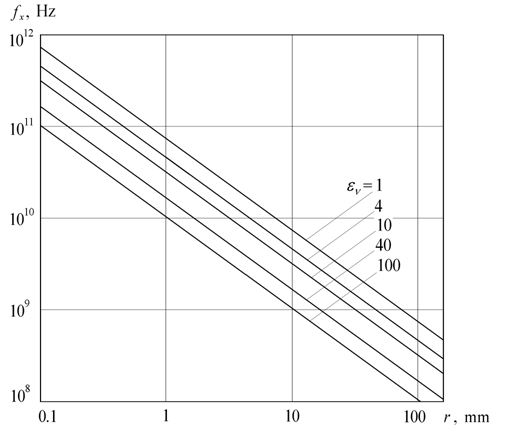
Рис. 4. Зависимость верхней граничной частоты рабочей области метода ЭПР от расстояния при e1=1 и фиксированных значениях относительной диэлектрической проницаемости подстилающего слоя e2.

 

На рис. 5 показаны зависимости погрешностей моделирования модуля и аргумента вектор-потенциала электромагнитного поля горизонтального   проводника   на   плоской   границе    немагнитных полупространств методом ЭПР от расстояния d до проводника; расстояние d измеряется в направлении, перпендикулярном продольной оси проводника. Границы заштрихованных областей соответствуют пятипроцентному (в обе стороны от номинального значения) разбросу значений диэлектрической проницаемости материала платы

или подложки (подстилающего слоя). Поскольку влияние технологического разброса размеров проводников и значений остальных параметров математической модели конструкции весьма мало по сравнению с влиянием названного фактора, можно сделать вывод о том, что метод ЭПР устойчив к технологическому разбросу значений параметров. Анализ и обобщение результатов вычислительного эксперимента, проведённого для проводников, часть которых представлена на рис. 5, подтверждает выводы, сделанные по результатам исследования погрешности моделирования поля диполя.

 

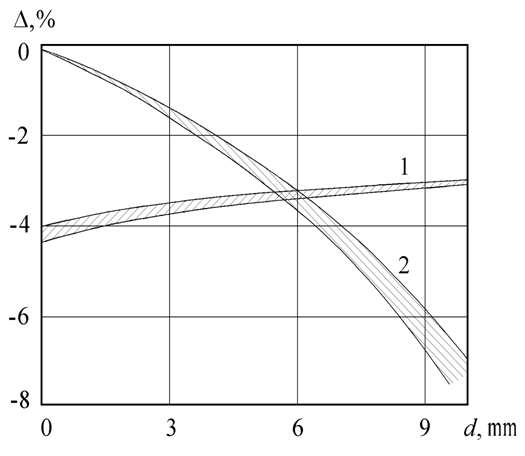
Рис. 5. Зависимость погрешности моделирования аргумента и модуля вектор-потенциала от расстояния до проводника-источника помехи (l=10 mm) при пятипроцентном (в обе стороны) разбросе значений относительной диэлектрической проницаемости подложки относительно номинального значения e2 = 8.5 на частоте f =3 GHz.

1 - область погрешности моделирования аргумента;

2 - область погрешности моделирования модуля.

 

Заключение

          Предлагаемый метод ЭПР позволяет моделировать поле далеко за пределами области квазистационарного приближения. Он приводит к математическим моделям, которые несколько уступают моделям, использующим строго динамический подход и пространственную дискретизацию моделируемого объекта, по диапазону рабочих частот, значительно превосходя их по экономичности (требуемому расходу машинного времени и требуемой ёмкости оперативной памяти).

 

Литература

1. Конников, И. А. Принципы организации подсистемы учёта конструктивно-технологических факторов при автоматизированном проектировании микросборок / И. А. Конников // Вопросы радиоэлектроники. Сер. ТПО: Научно-технический сборник / 1982. Bып. 3. С. 8 - 12.

2. Кечиев, Л. Н. Проектирование печатных плат для цифровой быстродейству-ющей аппаратуры / Л. Н. Кечиев. М.: ООО "Группа ИТД", 2007. 616 с.

3. Конников, И. А. Моделирование электромагнитных наводок в САПР электронных модулей // И. А. Конников / Вестник МГТУ им. Н. Э. Баумана. Cер. Приборостроение. 2007. №4(69). C. 3 - 20.

4. Конников, И. А. Метод эквивалентной постоянной распространения для моделирования электромагнитного поля в микроэлектронике / И. А. Конников //  Научная сессия ГУАП. Сб. докл.: В 3 ч.  Ч. II. Технические науки. / СПб ГУАП: СПб., 2008. С. 109 - 110.

5. Конников, И. А. Математическая модель конструкции микросхемы. / И. А. Конников //  Математическое моделирование. 2007. №4. С. 37 - 44.

6. Конников, И. А. Вычисление функции Грина для уравнения Лапласа // И. А. Конников / Журнал Технической Физики. 2007. № 1. C. 15 - 20.

7. Конников, И. А. Область корректного использования метода эквивалентной постоянной распространения. / И. А. Конников //  Научная сессия ГУАП. Сборник докладов: В 3 ч. Ч.II. Технические науки. / СПб ГУАП: СПб, 2008. С.111 - 115.

8. Конников, И. А. Вычислениe параметров переходного процесса в канале электромагнитной связи // И. А. Конников / Электромагнитные волны и электронные системы. 2007. № 11. C. 52 - 60.

9. Гринберг, Г. А. Избранные вопросы математической теории электрических и магнитных явлений / Г. А.  Гринберг. М.; Л.: АН СССР, 1948. 728 с.


[1]При использовании для реализации метода связанных линий вычислительных приёмов, описанных в настоящей работе, вычислительная ёмкость этого метода становится сравнимой с вычислительной ёмкостью предлагаемого метода эквивалентной постоянной распространения, однако известный вариант метода связанных линий предполагает учёт лишь статической составляющей поля.

[2] Так например, при указанных для рис.1 значениях параметров частота, на которой имеет место набег фазы , равна 35.399 GHz, причём на этой частоте Dм=-8.2% и Da=-2.87%.