УДК 621.396.962
Потенциальный предел и показатели качества сверхрэлеевского разрешения сигналов
С. А. Климов
лаборатория проблем обработки радиолокационной информации Военной академии войсковой ПВО
имени Маршала Советского Союза А. М. Василевского, Смоленск
Получена 8 июля 2013 г.
Аннотация. В статье проведена систематизация направлений поиска потенциального предела сверхрэлеевского разрешения и дан ответ на вопрос о существовании такого предела при решении задачи разрешения-обнаружения. Показано, что кривые вероятности полного разрешения сигналов определяют предел разрешающей способности при фиксированной вероятности ложной тревоги и коэффициенте корреляции сигналов. Методом имитационного моделирования для большого количества алгоритмов цифрового спектрального анализа оценена степень их приближения к потенциальному пределу сверхрэлеевского разрешения.
Ключевые слова: сверхрэлеевское разрешение, разрешающая способность, предел разрешения, показатели качества разрешения сигналов, цифровой спектральный анализ.
Abstract. Systematization of the directions of search of a potential limit of superrayleigh resolution is carried out and a question of existence of such limit at the solution of a problem of resolution detection is answered . It is shown that curve probabilities of full resolution of signals define a resolution limit at the fixed probability of a false alarm and coefficient of correlation of signals. The method of imitating modeling for a large number of algorithms of the digital spectral analysis estimated extent of their approach to a potential limit of superrayleigh resolution.
Keywords – superrayleigh resolution, resolution, resolution limit, indicators of quality of resolution of signals, digital spectral analysis.
Введение
Достаточно долгое время для радиоэлектронных систем различной физической природы предел разрешающей способности, установленный впервые в 1888 году Рэлеем, считался фундаментальным пределом, преодолеть который было невозможно. Основанием для этого стало то, что введенные им определение и критерий разрешения прекрасно подтверждались многочисленными экспериментами в различных областях радиотехники. Поэтому, со временем, эти понятия стали классическими.
С появлением новых методов обработки сигналов и получением в ряде случаев разрешения, превышающего установленное Рэлеем, классическое определение и предел разрешающей способности стали противоречить экспериментальным результатам. Начиная примерно с конца 50-х годов прошлого века, были разработаны первые методы сверхрэлеевского разрешения сигналов. Применительно к радиолокационным приложениям в работах [1–4] показана принципиальная возможность превышения рэлеевского предела разрешающей способности исключительно за счет обработки сигналов. Таким образом, считавшийся фундаментальным предел разрешающей способности, установленный Рэлеем, был успешно преодолен.
Однако широкому практическому применению методов сверхрэлеевского разрешения сигналов препятствовали высокие требования к объему и быстродействию существующей в то время вычислительной аппаратуры. Интенсивное развитие технологий цифровой обработки сигналов позволило в настоящее время устранить эту проблему и создало хорошие возможности для их реализации в радиоэлектронных системах различного назначения.
В связи с достаточно большим количеством методов сверхрэлеевского разрешения сигналов актуальной является задача сравнительной оценки их эффективности. Как правило, такие методы сравниваются не по совокупности, а по одному – двум частным, но наиболее выигрышным показателям качества. Не оговариваются четко и ясно условия, при которых были получены те или иные результаты. Часто при сравнительной оценке используются даже разные определения разрешающей способности. Все это создает серьезную проблему для специалистов при практическом применении того или иного метода высокого разрешения в радиоэлектронных системах. Кроме того, продолжаются поиски единого потенциального предела, к которому должны приближаться все методы сверхрэлеевского разрешения сигналов. Установление такого предела позволило бы расставить их в один приоритетный ряд по степени приближения к нему и сделать вывод о целесообразности дальнейшей работы по повышению разрешающей способности. Но самое главное это позволило бы ответить на вопрос о том, какие возможности в принципе заложены в методах, позволяющих за счет обработки сигналов обеспечить более высокую разрешающую способность, чем это определено критерием разрешения Рэлея. Установление потенциальной границы разрешения необходимо также для того, чтобы выявлять ошибочные методы сверхрэлеевского разрешения сигналов. Это становится возможным благодаря тому, что если потенциальный предел будет найден, то ни один из методов не сможет его преодолеть.
В связи с этим целью статьи является систематизация направлений поиска потенциального предела сверхрэлеевского разрешения и ответ на вопрос о существовании или отсутствии такого предела при решении задачи разрешения-обнаружения.
Существует четыре направления, в которых специалисты делают попытки получить потенциальный предел сверхрэлеевского разрешения. При этом каждое направление характеризуется своим определением разрешающей способности, показателями качества разрешения, методами сверхрэлеевского разрешения, а также ограничениями и допущениями.
Первое направление связано с решением задачи разрешения-обнаружения. В этом случае к разрешающей способности подходят со статистической точки зрения, по аналогии с теорией обнаружения [1,2,4,5]. Для задачи разрешения-обнаружения в работе [5] введены понятия полного разрешения и частные показатели качества разрешения сигналов. При этом под полным разрешением группы из М сигналов при наличии помех понимается принятие решения об осуществлении одного из 2М возможных несовместных событий в виде различных комбинаций наличия или отсутствия каждого из сигналов [5]. Предполагается, что число М разрешаемых сигналов известно, а сами сигналы могут характеризоваться определенным числом детерминированных или случайных параметров [1,2,4,5]. Вопрос о существовании предела для задачи разрешения-обнаружения будет рассмотрен ниже.
Второе направление связано с решением задачи разрешения-измерения. Для данного направления понятие разрешающей способности связывают с точностью оценки случайных параметров сигналов [6−10]. В общем виде критерий разрешения сигналов для этого направления можно сформулировать следующим образом. Сигналы разрешаются, если точность оценки параметров каждого из сигналов, не ниже заданной. Для решения задачи разрешения-измерения точность оценки параметров выражается, как правило, через математические ожидания, среднеквадратичные ошибки и дисперсии оценок [6−10]. Для данного направления предполагается, что число разрешаемых сигналов определено, задана их аналитическая форма и они имеют фиксированное количество случайных параметров.
Потенциальный предел при решении задачи разрешения-измерения установлен, т. к. известно, что существует нижняя граница точности любых несмещенных оценок [11]. Для любого из методов данного направления потенциальный предел сверхрэлеевского разрешения сигналов определяется неравенством Крамера–Рао. Иными словами, так же как и при оценке одного параметра сигнала, при разрешении сигналов существует минимальный корреляционный эллипсоид такой, что корреляционный эллипсоид произвольного набора несмещенных оценок всегда больше минимального
,
|
где |
|
– |
вектор наблюдений; |
|
|
|
– |
корреляционная матрица несмещенных оценок параметров сигналов; |
|
|
|
– |
информационная матрица Фишера [11]; |
|
|
|
– |
символ комплексно-сопряженного транспонирования. |
Таким образом, при решении задачи разрешения-измерения заданный объем корреляционного эллипсоида служит мерой разрешения сигналов, а его минимальный объем – потенциальным пределом. Необходимо отметить, что неравенство Крамера–Рао определяет границу эффективных и несмещенных оценок параметров разрешаемых сигналов в условиях регулярности целевой функции. Условия регулярности не всегда могут быть обеспечены. Как следствие, установить потенциальный предел становиться невозможным. Для некоторых случаев задачи разрешения-измерения сигналов потенциальный предел получен в работах [6−10 и др.].
Третье направление связано с решением задачи разрешения-обнаружения-измерения. При этом под разрешением сигналов понимается указание числа сигналов, содержащихся в реализации смеси сигналов и помех, и оценивание параметров всех обнаруженных сигналов [13,14]. Это направление является наиболее общим с теоретической и практической точек зрения. Как следует из определения разрешающей способности, для данного направления предполагается, что неизвестно как число разрешаемых сигналов, так и их параметры. В этом случае значительно сложнее становится поиск не только потенциального предела сверхрэлеевского разрешения, но и самого метода разрешения сигналов.
Например, метод максимального правдоподобия в его традиционной форме неприменим для синтеза алгоритмов разрешения-обнаружения-измерения, поскольку приводит к тривиальной оценке числа сигналов, принимающей с вероятностью близкой к единице их максимально допустимое значение [13]. Кроме того, препятствиями на пути установления границы сверхрэлеевского разрешения являются невозможность получения явных выражений для целевых функций, а также трудности аналитического исследования статистических характеристик получаемых оценок. Как правило, оценки являются смещенными. Это не позволяет найти для них нижнюю границу точности, определяемую неравенством Крамера–Рао. Смещение оценок отсутствует только в том случае, когда предполагаемое число сигналов равно их истинному числу. В этом случае мы снова приходим к задаче разрешения-измерения и, установление потенциального предела сводится к ранее рассмотренной задаче нахождения минимального объема корреляционного эллипсоида оценок параметров разрешаемых сигналов.
Четвертое направление связано с информационным подходом к понятию разрешающей способности [12]. Это следует из того, что интегральное уравнение Фредгольма 1-го рода, устойчивое решение которого требуется получать при сверхрэлеевском разрешении сигналов, совпадает с интегральным уравнением свертки, описывающим прохождение переданного сигнала через канал связи с шумом. Для такого канала хорошо известна формула Шеннона, связывающая между собой скорость передачи информации с полосой пропускания канала и отношением сигнал-шум. Скорость передачи информации, в свою очередь, можно трактовать как передачу определенного числа различимых (разрешаемых) сигналов в единицу времени. В связи с этим, в работе [12] показано, что для информационного подхода предел сверхрэлеевского разрешения сигналов определяется уровнем шума во входных данных и может быть вычислен по формуле, следующей из теоремы Шеннона:
,
|
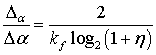где |
|
– |
рассогласование сигналов по разрешаемому параметру; |
|
|
|
– |
ширина характеристики (импульсной, частотной или пространственной) системы, определяющая ее разрешающую способность по Рэлею; |
|
|
|
– |
коэффициент, зависящий от точного вида определения ширины характеристики системы [12]; |
|
|
|
– |
отношение сигнал-шум. |
Вернемся к
вопросу о существовании предела для задачи разрешения-обнаружения. Для этого остановимся
более подробно на эффективности методов сверхрэлеевского разрешения сигналов. Введем
показатели качества разрешения. Качество полного разрешения целесообразно оценивать матрицей
условных вероятностей 
, содержащей 
матричных элементов [5]. Элементом 
матрицы Р является вероятность принятия решения о
событии i при условии, что в действительности имеет место событие j. Матричные элементы с
равными индексами i = j характеризуют условные вероятности принятия
правильных решений, а с неравными индексами i ≠ j – ложных решений.
В частности, для полного
разрешения двух сигналов (
) имеем следующую
матрицу условных вероятностей:
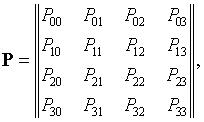(1)
|
где |
|
– |
вероятность правильного необнаружения сигналов; |
|
|
|
– |
вероятность правильного обнаружения первого (второго, двух сигналов); |
|
|
|
– |
вероятность ложной тревоги при обнаружении первого (второго, двух) сигналов; |
|
|
|
– |
вероятность пропуска первого (второго, двух) сигналов; |
|
|
|
– |
вероятность перепутывания при обнаружении первого (второго) сигналов; |
|
|
|
– |
вероятность перепутывания при обнаружении первого (двух) сигналов; |
|
|
|
– |
вероятность перепутывания при обнаружении второго (двух) сигналов. |
В геометрической интерпретации указанные выше вероятности показаны
на рисунке 1. Они равны площадям фигур, ограниченных соответствующими
плотностями вероятности и порогами 
. Например,
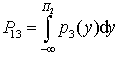или
,
|
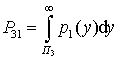где |
|
– |
плотность вероятности суммы первого, второго сигнала и шума; |
|
|
|
– |
плотность вероятности суммы первого сигнала и шума. |
Поскольку, соответствующие одному и тому же условию (нет сигналов, присутствуют первый, второй или два сигнала) решения (сигналов не обнаружено, обнаружен первый, второй или два сигнала) взаимоисключающие, то выполняются равенства:
, 
.
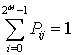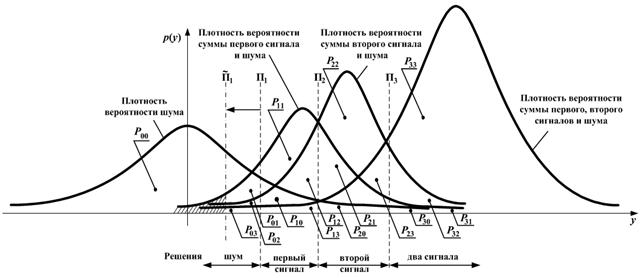
Рисунок 1 – Пояснение к
формированию элементов матрицы 
, характеризующей
качество полного разрешения двух сигналов
Система показателей качества полного разрешения может характеризоваться различными вариантами выбора из матрицы (1) независимых матричных элементов. Например, в качестве таковых могут выступать:
1) вероятности
ошибочных решений , i ≠ j;
2)
вероятности 
, 
, 
, 
и 
;
3) вероятности 
, 
, 
, 
и 
;
4) вероятности 
, 
, 
, 
и 
;
5) вероятности 
, 
, 
, 
и 
.
Рассмотрим первую
систему показателей. Матричные элементы 
, 
можно
объединить, введя результирующую вероятность ложной тревоги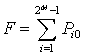 
. По аналогии с теорией обнаружения при
оценке качества разрешения сигналов условную вероятность 
будем задавать априори, и ограничивать ее
сверху достаточно малой величиной. Для решения задач сверхрэлеевского
разрешения сигналов ее целесообразно выбирать порядка 
.
К разрешению сигналов, как правило, переходят после
обнаружения хотя бы одного сигнала, т. е. превышения порога обнаружения 
, показанного на рисунке 1. В этом случае, выбирая в
диапазоне (достаточно
большой для задачи классического обнаружения) за счет сдвига порога от П1
к 
, обеспечивается
весьма малое значение «хвостов» распределений смеси первого, второго или
двух сигналов с шумом. «Хвосты» распределений определяются вероятностями и показаны на рисунке 1 штриховкой
после выставления порога , соответствующего
результирующей вероятности ложной тревоги . Поэтому достаточно корректно допущение, что матричные
элементы 
, 
, характеризующие вероятности пропуска
первого, второго и двух сигналов, будут близки к нулю. В этом случае можно записать
, 
и 
. В целом, система показателей качества вместо
девяти теперь характеризуется четырьмя следующими значениями: априори заданной
результирующей условной вероятностью ложной тревоги и
условными вероятностями правильного обнаружения первого, второго и двух сигналов
, и .
Таким образом, мы
получили удобную систему показателей качества для оценки эффективности полного
разрешения двух сигналов. Рассмотренный подход достаточно просто можно
распространить на число разрешаемых сигналов больше двух, но в данной статье
ограничимся только двумя. Заметим, что если каждый из 
сигналов
разрешен и известна вероятность его обнаружения 
, то
вероятность полного разрешения сигналов (фактически
определения числа сигналов) рассчитывается как вероятность независимых событий,
т. е.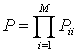 
. Например, вероятность полного разрешения
двух сигналов с одинаковой энергией 
соответствует
вероятности правильного обнаружения каждого отдельного сигнала 
, а 
соответствует
. Полученная
система показателей качества используется
ниже для оценки эффективности полного
разрешения двух сигналов.
На основе результатов, изложенных в работах [4,5], были получены оценки эффективности методов сверхрэлеевского разрешения Я. Ширмана [5] и К. Хелстрома [4]. Метод Я. Ширмана, в основе которого лежит байесовский подход, выбран потому, что он реализует оптимальный алгоритм разрешения сигналов при полной статистической априорной информации о них. Метод К. Хелстрома, в основе которого лежит метод максимального правдоподобия (наименьших квадратов), выбран потому, что он широко распространен на практике в самых различных областях радиотехники. Кроме того, оценки максимального правдоподобия обладают свойством состоятельности и асимптотической эффективности.
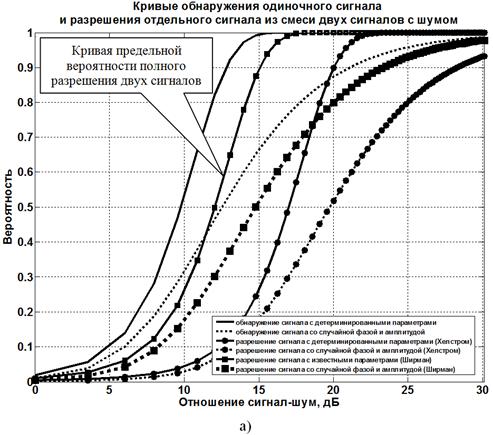
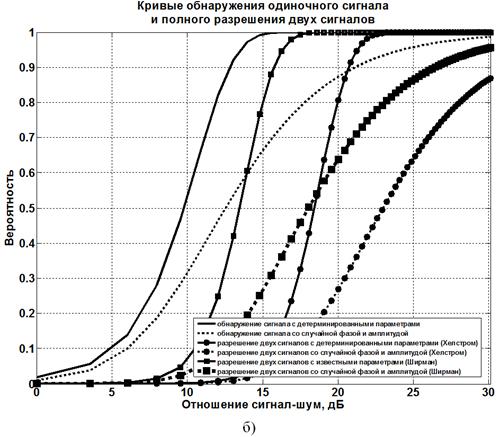
Результаты
расчетов представлены на рисунках 2−4 в виде кривых обнаружения
отдельного сигнала 
из смеси двух сигналов с шумом (рисунки 2а–4а) и кривых полного разрешения двух сигналов (рисунки 2б–4б) в зависимости от
отношения сигнал-шум. Графики построены при вероятности ложной тревоги 
и
фиксированных коэффициентах
корреляции 
сигналов 0,9 (рисунок 2),
0,5 (рисунок 3) и 0,2 (рисунок 4). На рисунках 2−4 построены
также классические кривые обнаружения для одиночного сигнала. Сплошными линиями
на рисунках показаны характеристики для сигналов с детерминированными
параметрами, а пунктирными – со случайной амплитудой и фазой. Маркером в виде
квадрата на всех рисунках показаны вероятности разрешения для метода
Я. Ширмана, а в виде кружка для метода К. Хелстрома. Необходимо отметить,
что графики на рисунках 2–4 построены для определенных F и . Тем
не менее, руководствуясь индуктивным методом познания можно заключить, что сделанные
ниже выводы являются справедливыми и в общем случае. Разница будет только в
конкретных численных показателях.
Из
анализа графиков, представленных на рисунках 2−4, следует ряд важных
выводов. Первый из них касается количественных показателей качества полного
разрешения сигналов. Видно, что эффективность рассматриваемых методов
сверхрэлеевского разрешения при коэффициенте корреляции сигналов ρ=0,5, т. е. когда уже превзойден рэлеевский предел
разрешающей способности, достаточно высока. Например, для сигналов со случайными
амплитудами и фазами при отношении сигнал-шум 20 дБ, вероятности ложной
тревоги F=0,001 и коэффициенте корреляции сигналов ρ=0,5, вероятность полного разрешения двух сигналов составляет около 0,7 (см. рисунок
3б).
Второй вывод затрагивает сравнительную оценку эффективности методов. Как видно из представленных результатов кривые разрешения для метода Я. Ширмана смещены по оси абсцисс влево относительно кривых разрешения К. Хелстрома. Другими словами, метод разрешения Я. Ширмана на основе байесовского подхода при прочих равных условиях эффективней метода разрешения К. Хелстрома, в основу которого положены оценки максимального правдоподобия (наименьших квадратов).
|
|
|
|
Рисунок 2 – Оценки эффективности методов сверхрэлеевского разрешения
Я. Ширмана и К. Хелстрома при вероятности ложной тревоги F=0,001
и коэффициенте корреляции сигналов ρ=0,9
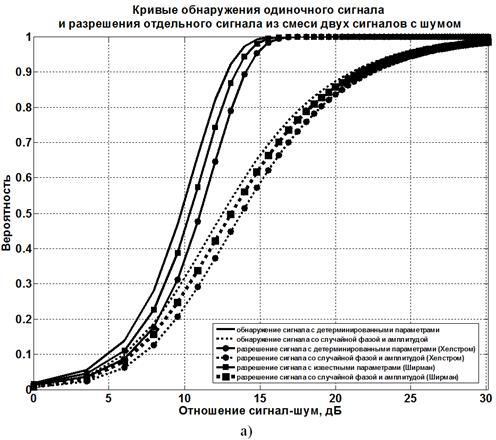
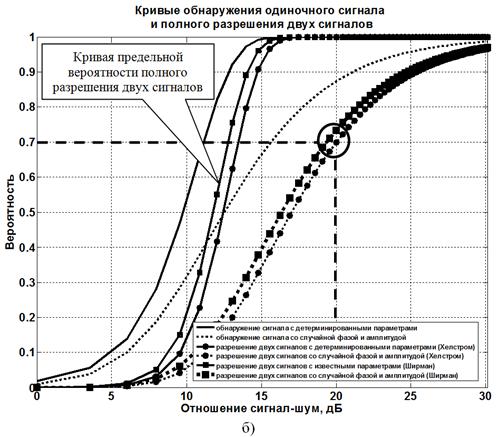
Рисунок 3 – Оценки эффективности методов сверхрэлеевского разрешения
Я. Ширмана и К. Хелстрома при вероятности ложной тревоги F=0,001
и коэффициенте корреляции сигналов ρ=0,5
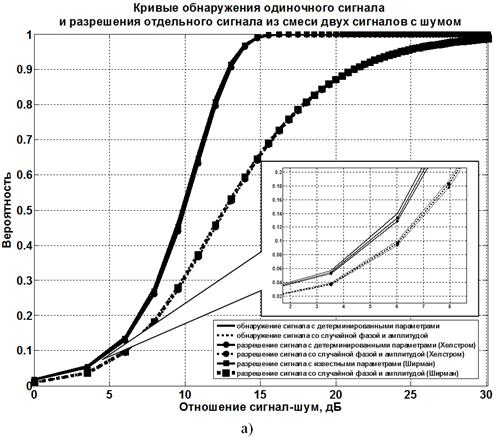
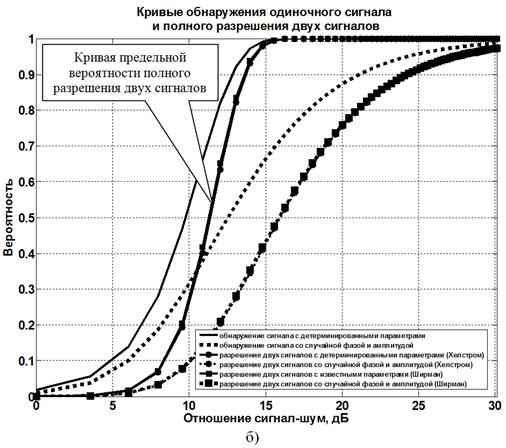
Рисунок 4 – Оценки эффективности методов сверхрэлеевского разрешения
Я. Ширмана и К. Хелстрома при вероятности ложной тревоги F=0,001
и коэффициенте корреляции сигналов ρ=0,2
Связано это с тем, что алгоритм разрешения К. Хелстрома не использует априорные данные о законах распределения амплитуд случайных сигналов [5]. Таким образом, рациональное использование достоверной априорной информации о разрешаемых сигналах повышает эффективность сверхрэлеевского разрешения. Отметим также, что с уменьшением коэффициента корреляции сигналов кривые разрешения Я. Ширмана и К. Хелстрома начинают приближаться друг к другу и примерно с величины ρ=0,2–0,3 практически совпадают (см. рисунок 4б).
Третий вывод подводит нас к ответу на вопрос о существовании потенциального предела сверхрэлеевского разрешения сигналов при решении задачи разрешения-обнаружения. До сих пор поиски такого предела связывались только с двумя показателями. Это отношение сигнал-шум и относительное рассогласование сигналов по разрешаемому параметру (параметрам). Но из проведенного анализа, следует, что граница сверхрэлеевского разрешения зависит от метода разрешения, априорной информации о разрешаемых сигналах, их числа, показателей качества разрешения (вероятностей правильного обнаружения отдельного сигнала из смеси сигналов с шумом и вероятности ложной тревоги), коэффициента корреляции сигналов. Из рисунков 2а–4а видно, что при заданной вероятности ложной тревоги и фиксированном коэффициенте корреляции сигналов кривые разрешения отдельного сигнала имеют вполне определенное значение. Превысить их невозможно в принципе, как невозможно превысить вероятности обнаружения одиночного сигнала. Следовательно, кривые полного разрешения двух сигналов и определяют искомый предел разрешающей способности в заданных условиях (см. рисунки 2б–4б). Кривые предельных вероятностей полного разрешения двух сигналов показаны на рисунках 2б–4б. В данном случае это кривые, соответствующие методу разрешения Я. Ширмана. Последнее закономерно, т. к. метод разрешения Я. Ширмана использует исчерпывающую статистическую априорную информацию о сигналах в сочетании с оптимальным алгоритмом их разрешения.
Теперь, когда установлен предел разрешения, мы можем ответить на важный практический вопрос. Известно, что существует большое количество методов цифрового спектрального анализа, обеспечивающих сверхрэлеевское разрешение сигналов. Как близки эти методы по своей эффективности к потенциальным характеристикам разрешения?
Для ответа на этот вопрос путем имитационного моделирования была исследована эффективность ряда известных методов цифрового спектрального анализа. Сравнительная оценка выполнялась для следующих методов: Берга, ковариационного, модифицированного ковариационного, MUSIC и EV. Кроме того, была исследована эффективность разрешения сигналов в частотной области непосредственно по корням характеристического полинома [13,14], а также методов, рассмотренных в работах [15,16]. При моделировании порядок модели (размер сигнального подпространства) выбирался исходя из достижения максимальной эффективности каждого из методов по вероятности полного разрешения двух гармонических сигналов.
Моделировалась аддитивная смесь
гармонических сигналов с шумом длиной N временных отсчетов с периодом дискретизации T секунд, состоящая из двух синусоид
при их взаимном рассогласовании по частоте 
=0,5
рэлеевского интервала разрешения, равного 1/NT Герц. Взвешивание сигналов во временной области не проводилось.
В этом случае коэффициент корреляции сигналов по частоте составил ρ=0,7. Фазы сигналов полагались случайными и распределенными
по равномерному закону в диапазоне значений 0–2π. Амплитуды гармонических
сигналов также полагались случайными, но распределенными по Рэлеевскому закону
с заданным параметром распределения. Амплитуды квадратурных составляющих
комплексного шума были распределены по нормальному закону. Все оценки получены
по результатам 100 независимых реализаций, что обеспечивало точность
статистического эксперимента порядка 10 % [17]. Порог устанавливался по
аналогии с критерием Неймана-Пирсона. При этом априори задавалась вероятность
ложных тревог F. Это значит,
что в отсутствии сигнала вероятность превышения заданного порогового значения
не превышала F. При
моделировании оценка вероятности ложной тревоги 
составляла
величину равную 5·10–2.
Отношение
сигнал-шум 
оценивалось на момент принятия решения о
разрешении сигналов, т. е. на выходе алгоритма обработки по формуле 
, где 
– отношение
сигнал-шум для одного сигнала на входе. Отношение сигнал-шум на входе задавалось как отношение среднего значения
(математического ожидания) 
случайной амплитуды
синусоиды к среднеквадратичному значению шума 
. При
этом для известного значения математического ожидания определялся
параметр распределения Рэлея 
в соответствии с
известным выражением 
[17].
Семейство
кривых полного разрешения двух сигналов для указанных методов цифрового спектрального
анализа представлено на рисунке 5. На нем же показаны кривые полного
разрешения двух сигналов для методов Я. Ширмана и К. Хелстрома, построенные
для аналогичных моделей сигналов, показателей качества и коэффициента
корреляции.
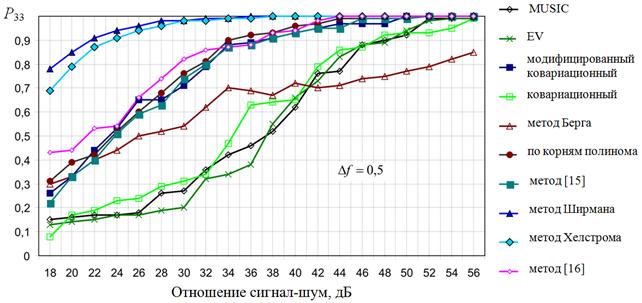
Рисунок 5 – Оценки вероятности полного
разрешения двух сигналов
для методов спектрального анализа. Вероятность ложной тревоги F=0,05.
Взвешивание отсутствует. Коэффициент корреляции сигналов ρ=0,7
Сравнительный анализ эффективности методов цифрового спектрального анализа (см. рисунок 5) показывает, что при равных показателях качества разрешения двух сигналов они еще очень далеки от предельного разрешения, обеспечиваемого методами Я. Ширмана и К. Хелстрома. Причем динамика падения эффективности возрастает при снижении отношения сигнал-шум. Вместе с тем это свидетельствует о том, что потенциал методов цифрового спектрального анализа еще не исчерпан.
Таким образом, анализ эффективности методов сверхрэлеевского разрешения сигналов показывает, что понятие «потенциальный предел» весьма условно. Конкретная эффективность решения задачи сверхрэлеевского разрешения сигналов зависит от многих факторов, определяющими из которых являются принятое определение разрешающей способности, метод сверхрэлеевского разрешения, система выбранных показателей качества и количество априорной информации о сигнале: его форма, число разрешаемых сигналов, количество разрешаемых параметров сигналов, детерминированные или случайные эти параметры и т. д.
Основной вывод статьи заключается в том, что в условиях заданной статистической априорной информации кривые разрешения отдельных сигналов жестко определены и не могут быть превышены. Тогда кривые вероятности полного разрешения определяют предел разрешающей способности при фиксированной вероятности ложной тревоги и коэффициенте корреляции сигналов.
Таким образом, граница разрешения теперь связана не только с отношением сигнал-шум и коэффициентом корреляции сигналов, но и с показателями качества разрешения. Предельные вероятности полного разрешения сигналов при заданной вероятности ложной тревоги и отношении сигнал-шум могут быть достигнуты в реальных радиоэлектронных системах. Для этого должна быть доступна вся априорная информация о сигналах и реализован оптимальный метод их сверхрэлеевского разрешения. Но они никогда не могут быть превышены.
В целом, можно заключить, что при заданных показателях эффективности, коэффициенте корреляции сигналов, функции потерь и видах законов распределения случайных амплитуд и фаз сигналов метод разрешения Я. Ширмана, в основе которого лежит байесовский подход, будет определять потенциальный предел сверхрэлеевского разрешения, т. к. использует исчерпывающую априорную информацию о сигналах в сочетании с оптимальным алгоритмом разрешения. Следовательно, показатели эффективности разрешения в этом случае будут предельными, поскольку с уменьшением априорных сведений качество сверхрэлеевского разрешения сигналов может только снижаться.
Метод К. Хелстрома, будет определять потенциальный предел сверхрэлеевского разрешения среди различных модификаций алгоритмов максимального правдоподобия и наименьших квадратов, которые используют существенно меньше априорной информации при разрешении сигналов.
Таким образом, указанные методы могут служить своего рода «эталоном» качества для вновь создаваемых алгоритмов сверхрэлеевского разрешения, которые все больше и больше совершенствуются с целью для достижения потенциального предела разрешающей способности.
1. Ширман Я. Д. Теория обнаружения полезного сигнала на фоне гауссовых шумов и произвольного числа мешающих сигналов со случайными амплитудами и начальными фазами//Радиотехника и электроника. 1959. Т. 4. .№ 12. С. 1176-1192.
2. Ширман Я. Д. Статистический анализ оптимального разрешения//Радиотехника и электроника. 1961. Т. 6. .№ 8. С. 1237-1246.
3. Nilsson N. J. On the optimum range resolution of radar signals in noise. IRE Trans. Information Theory, vol. IT-7, Oct. 1961, pp. 245–253.
4. Хелстром К. Статистическая теория обнаружения сигналов. М., Изд-во иностр. лит., 1963. 432 с.
5. Ширман Я. Д. Разрешение и сжатие сигналов. М., Сов. радио, 1974. 315 с.
6. Сверлинг Р. Максимальная точность определения угловых координат импульсной радиолокационной станцией//Вопросы РЛТ. Т. 2(88). 1957.
7. Царьков Н. М. Многоканальные радиолокационные измерители. М., Сов. радио, 1980. 192 с.
8. Слюсар В. И. Предельное разрешение дальномерных процедур максимального правдоподобия//Радиоэлектроника. 1998. № 11. С. 39−45.
9. Проскурин В. И. Потенциальная разрешающая способность радиолокационной станции//Радиотехника. 2001. № 5. С. 67−70.
10. Монаков А. А., Мишура Т. П. Потенциальная разрешающая способность РЛС по дальности//Успехи современной радиоэлектроники. 2008. № 12. С. 31–34.
11. Косарев Е. Л. Методы обработки экспериментальных данных. М., Физматлит, 2008. 208 с.
12. Косарев Е. Л. О пределе сверхразрешения при восстановлении сигналов//Радиотехника и электроника. 1990. Т. 35. № 1. С. 68-87.
13. Трифонов А. П., Шинаков Ю. С. Совместное различение сигналов и оценка их параметров на фоне помех. М., Радио и связь, 1986. 264 с.
14. Марпл С. Л. Цифровой спектральный анализ и его приложения. М., Мир, 1990.
15. Савинов Ю. И. Когерентный метод Прони с квазипрореживанием//Вопросы радиоэлектроники. Серия РЛТ. 2008. Вып. 3. С. 123–128.
16. Григорян Д. С. Принципы когерентной обработки данных в задачах спектрального анализа сигналов в радиолокаторах со сверхразрешением//Вопросы радиоэлектроники. Серия РЛТ. 2012. Вып. 2. С. 93–108.
17. Вентцель Е. С. Теория вероятностей. М., Издательский центр «Академия», 2003. 576 с.