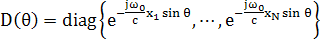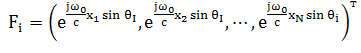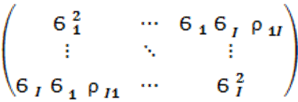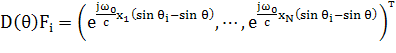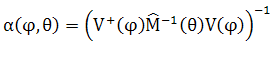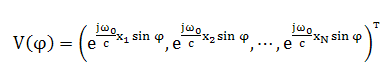УДК 621.391, 621.396

УГЛОВОЕ РАЗРЕШЕНИЕ ИСТОЧНИКОВ КОРРЕЛИРОВАННЫХ СИГНАЛОВ С ИСПОЛЬЗОВАНИЕМ ПСЕВДОСЛУЧАЙНОЙ ОБРАБОТКИ

 

И. Г.  Серебряков, Г. В. Серебряков

Научно-Исследовательский Институт Ситроникс

 

Получена   1 августа    2013 г.

 

Аннотация.  В работе предложен  нелинейный метод углового разрешения взаимно коррелированных сигналов в антенных решетках, основанный на псевдослучайной пространствен­ной обработке и свободный от ряда  недостатков, которые присущи широко известным методам, предназначен­ным для той же цели. Эффективность предлагаемого метода продемонстрирована с помощью численного моделирования. Обсуждаются возможности его применения при адаптивном формировании диаграммы направленности в условиях, когда помеховые сигналы коррелированы с полезным.

Ключевые слова: коррелированные сигналы, угловое сверхразрешение, антенные решетки.

Abstract: In the paper a nonlinear method of high angular resolution of multiple coherent and incoherent signal sour­ces is introduced. This technique uses spatial pseudorandom array processing and is free from some disadvantages of the earlier methods. The results of   computer simulations are shown. The pos­sibilities of this technique in adaptive beamforming are discussed.

Key words: correlated sources, angular superresolution, antenna array.

 

1.     Введение

Наличие взаимной коррелированности сигналов, приходящих с различных на­правлений, характерно для гидроакустики, радиолокации и ряда других областей,  вследствие эф­фекта многолучевого распространения   [1-5] . В связи с этим боль­шое внимание привлекает задача углового разрешения сигналов с произ­вольной степенью взаимной коррелированности в антенных решетках (АР).  Обычно, для углового разрешения узкополосных сигналов в АР широко используют нелинейные методы спектрального анализа, позволяющие достигать повышенной разрешающей способности (так называ­емого эффекта сверхразрешения) по сравнению с классическим линейным методом. Однако, как показано в большом числе работ (см., например,  [4-10]) , наличие вза­имной корреляции сигналов, приходящих с различных направлений, приво­дит к потере работоспособности данных методе, тем более серьезной, чем выше уровень такой взаимной корреляции. Известен ряд искусст­венных процедур, позволяющих повысить их эффективность в этом случае.  Подобные процедуры основаны на декорреляции сигналов с. помощью прост­ранственного сглаживания корреляционной матрицы скользящей подрешеткой [6-9]. Однако, эти методы имеют ряд существенных недостатков, ограничивающих их применение на практике. Для успешной работы данных процедур требуется, чтобы АР была линейной, эквидистантной, имела идентичные приемные элементы, а  сигналы имели плоские волновые фронты. Всем этим требованиям зачастую не удается удовлетво­рить на практике. Кроме того, использование скользящей подрешетки приводит к уменьшению эффективного размера апертуры [6,7,9], что обуславливает дополнительные потери в разрешении.

В настоящей работе  предлагается нелинейный метод углового разрешения взаимно коррелированных сигналов, осно­ванный на псевдослучайной пространственной обработке входных сигна­лов АР и свободный от указанных выше недостатков.

2. Псевдослучайная пространственная обработка сигналов в АР

Рассмотрим    N-элементную АР, на которую приходят I узкополосных внешних сигналов с различных направлений. Для про­стоты рассмотрения будем считать, что АР линейна, имеет изотропные элементы, а волновые фронты сигналов являются плоскими, хотя данные условия не являются обязательными для работы предлагаемого метода и обобщение на случай произвольной геометрии АР, неидентичных приемных элементов и более сложной модели распространения проводится стандарт­ным образом. Вектор входных сигналов АР (размерности   N)  , сфазированной в направлении    записывается в виде

,                                                  (1)

 

где

                                   (2)

 

- диагональная унитарная матрица размерности NхN, А – матрица размерности NxI , которую можно записать в следующем виде

где

                               (3)

 

- вектор амплитудно-фазового распределения, наводимого в элементах АР i-м сигналом,   приходящим с направления    ,  

S(t) - вектор размерности  I  -  комплексных амплитуд сигналов,  

n(t)- вектор размерности N собственных шумов в элементах АР,

ω - центральная частота сигналов,  с  - фазовая скорость,  

 - координата i-го приемного элемента вдоль линии апертуры,  (т) – знак транспортирования.  Углы и, i = 1,I отсчитываются от нормали к апертуре. Взаимная корреляция сигналов описывается корреляционной матрицей их комплексных амплитуд

                                                                    (4)

 

где (+) и <·> - знаки эрмитового сопряжения и статистического усред­нения, соответственно. Известно, что данная матрица имеет следующий вид   [5-7]

 

Q =                             (5)

 

 

где

 

                                 (6)

 

 

- комплексный коэффициент корреляции    k-го и l-гo сигналов в начале координат,    - мощность      l-го сигнала в приемном элементе АР.

Под псевдослучайной пространственной обработкой   мы будем понимать случайные перестановки элементов каждого из векторов входных сигналов (1). Подобные перестановки, очевидно, техни­чески могут быть осуществлены путем случайных переключений приемных элементов решетки или электронным перемешиванием отсчетов с разных элементов антенны при наборе выборки для оценивания  корреляционных характеристик принимаемых сигналов. Вводя оператор    ( …)   случайной перестановки элементов вектора Х(t,Ө) запишем вектор размерности N     входных сигналов после операции псевдослучайной пространственной обработки в виде

                                                   (7)

 

Оператор  (·) зависит от времени, так как для различных моментов вре­мени случайные перестановки должны быть различными. Качественно рассмотрим влияние псевдослучайной обработки на вектор направления произвольного i-го сигнала после операции фазирования. Согласно (2),(3) данный вектор запишется в виде

                         (8)

 

Если АР точно сфазирована на    i-й сигнал, то согласно (8), подобные случайные перестановки не влияют на прием данного сигнала, так как его запаздывания между элементами АР скомпенсированы за счет опера­ции фазирования ( =  и поэтому вектор направления данного сигнала после фазирования имеет одинаковые элементы, равные единице). Сигналы, приходящие с направлений, отличных от того, на которое сфазирована антенна, имеют различные запаздывания в разных приемных элементах. Поэтому   под воздействием псевдослучайной пространственной обработки (7) происходит "разрушение" данных сигналов и перекачка их в собст­венные шумы.

Введем пространственную корреляционную матрицу входных сигналов АР после псевдослучайной обработки следующим образом:

                                              (9)

 

Выборочная оценка этой матрицы имеет вид

                                           (10)

где   J - число статистически независимых выборок вектора Y(t,). В силу вышеописанных свойств псевдослучайной пространственной обработ­ки, матрица  будет иметь интенсивную компоненту вида  SS+  при совпадении направления прихода какого-либо сигнала и направления фа­зирования    , где S -  вектор размерности   N    амплитудно-фазового распределения, наводимого сигналом, на который сфазирована АР с компонентами

                                                         (11)

Только в этом случае, псевдослучайная обработка не разрушает сигнал, падающий на АР. При увеличении рассогласования между направлением фазирования    и направ­лением прихода сигнала, интенсивность данной компоненты в матрице  будет уменьшаться. Таким образом, факт прихода какого-либо сигнала с направления     можно установить путем выявления в выборочной кор­реляционной матрице  компоненты   SS+. Для этого удобно воспользоваться нелинейным методом сверхразрешения Кейпона, поскольку данный метод при разрешении формирует спектральные пики, пропорцио­нальные мощностям разрешаемых сигналов  [1-3]. Соответствующая спек­тральная оценка будет иметь вид

 

                                           (12)

где

 

                                (13) 

 

- вектор размерности N обзора по условно вводимому углу φ.  При значении φ=0,  величина (12) характеризует интенсивность компоненты SS+ выборочной корреляционной матрице  при заданном угле фазирования . Этот факт можно использовать для углового разрешения сигналов, осуществляя обзор пространства по углу  при φ= 0. Учитывая, что при φ=0 (13) совпадает с (11), получаем из (12) оценку углового спектра вида:

                                                  (14)

Таким образом, предлагаемый метод углового разрешения сигналов включает   в себя сле­дующие этапы:

1. Параллельное  фазирование АР на различные направления путем формирования веера лучей для обзора пространства с требуемым шагом по углу. Математически эта операция сводится к формированию в момент t
совокупности векторов  Х(t,) отличающихся значениями    .

2. Псевдослучайная обработка при соответствующих параметрах  t    ,       в соответствии с (7).

3. Оценивание совокупности пространственных корреляционных матриц при различных значениях параметра        по формуле (10).

4. Вычисление результирующей оценки углового спектра (14).

 

3. Результаты моделирования

Для исследования эффективности предложенного метода нелинейного спектрального анализа в случае разрешения взаимно коррелированных сиг­налов было проведено численное моделирование при условии конечного числа статистически независимых выборок. Моделировалось воздействие узкополосных сигналов с плоскими волновыми фронтами на десятиэлементную линейную эквидистантную АР с межэлементным расстоянием d=λ/2, где     λ - длина волны. Начало координат при моделировании было выбрано в первом элементе решетки. Мощности сигналов задавались одинаковыми и равными 20 дБ по отношению к мощности собственного шума в одном элементе АР. Собственные шумы полагались равными по мощности в каждом приемном элементе и статистически независимыми по элементам. Корреляционные матрицы (9) оценивались по формуле (10) с использова­нием   100 статистически независимых выборок входных сигналов АР.

В первом численном эксперименте моделировалось разрешение двух полностью коррелированных сигналов (‌= 1) с углами прихода      = 3°,   = -3° . Аргумент коэффициента корреляции задавался равным нулю. На рис. 1 изображена оценка углового спектра (14). Истинные угловые координаты сигналов помечены стрелками. Во втором численном эксперименте было задано пять полностью коррелированных сигналов с угловыми координатами =0° , =-15°, =-30° ,  =15°, =30°. Аргументы всех коэффициентов корреляции задавались равными нулю. На рис. 2 приведена оценка углового спектра (14) для этого случая. Поскольку предельное разрешение для   линейного метода составляет в рассматриваемых случаях примерно 10°,  из рис. 1 следует, что в первом численном эксперименте имеет место эффект сверхразрешения, так как наблюдаются раздельные максимумы в спектральной оценке, соответствующие сигналам,  разнесенным на 6º. При этом разница между максимумами и провалом в угловом спектре составляет 3 дБ, а смещение данных максимумов относительно истинных угловых координат сигналов не превышает 1,4º. Во втором численном эксперименте спектральная оценка (14) имеет более резко выраженные максимумы.

Отметим, что предложенный метод может быть использован при адап­тивном формировании диаграммы направленности (ДН) в антенных решетках в случае, когда полезный и помеховые сигналы являются взаимно коррелированными. Как известно, классический подход к адаптивной обработке в данной ситуации натал­кивается на трудности, аналогичные описанным выше для методов угло­вого разрешения. Так, при взаимной коррелированности возникает нежелательный эффект подавления полезного сигнала помеховыми [5-8], что приводит к резкому падению эффективности адаптивной обработки. Использование спектральной оценки (14) позволяет проводить адаптивное формирование ДН в два этапа, избежав данного нежелательного эффекта. Сначала с помощью (14) определяются угловые координаты помеховых сиг­налов, а затем с помощью известных методов синтеза антенн   [11-12]   фор­мируются провалы в диаграмме направленности в соответствующих направ­лениях. Требуемая ширина провала может регулироваться с помощью нало­жения ограничений на производные диаграммы направленности, поскольку она определяется дисперсиями оценок угловых координат сигналов [12].

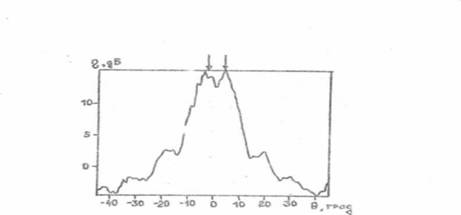
Рис. 1. Разрешение  двух полностью коррелированных сигналов при  J = 100, N=10, d=λ/2,    = 3°,   = -3°.
Отношение мощности каждого из сигналов к мощности, собственного шума в приемном элементе АР равно 20 дБ

 

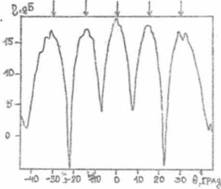
Рис.2. Разрешение пяти полностью коррелированных сигналов при   J = 100 , N=10 , d =λ/2, =0° , =-15°, = -30° ,  = =15°, = 30°. Отношение мощности каждого из сигналов к мощности собственного шума р. приемном элементе АР равно 20 дБ.

 

4. Заключение

Предложен нелинейный метод углового разрешения вза­имно коррелированных сигналов в АР, основанный на  псевдослучайной пространственной обработки.  Данный подход позволяет работать со статистически независимыми выборками входных сигналов решетки и легко обобщается на случай многомерной АР с произвольным расположением и характеристиками приемных элементов, а также не случай более сложных моделей распространения (сферические волновые фронты и т.п.).

 

Работа была частично поддержана РФФИ (№11-02-01216-а).

Литература

1.     Пистолькорс А.А., Литвинов О.С. Введение в теорию адаптивных антенн. -М.: Наука, 1991. 200 с.

2.     Ширман Я.Д., Манжос В.Н. Теория и техника обработки радиолокацион­ной информации на фоне помех. - И.: Радио и связь, 1981.- 416 с.

3.     Гейбриэл У.Ф. Спектральный анализ и методы сверхразрешения с ис­пользованием адаптивных решеток // ТИИЭР. - 1980. -- Т.68, № 6, -С.19-32.

4.     Литвинов O.C. О теории адаптивных антенных решеток в условиях коррелированных помеховых сигналов //  Сб. "Антенны". - М.: Радио и связь. 1981. Вып.'29. - С.67-79.

5.     Shan T. and Kailath T. "Adaptive beamforming for coherent signals and interference"// IEEE Trans. Acoust., Speech, Signal Processing, vol. ASSP-33, pp.527 -536 1985.

6.     Reddy V. U., Paulraj A. and Kailath T. "Performance analysis of the optimum beamforming in the presence of the correlated sources and its behavior under spatial smoothing" //IEEE Trans. Acoust., Speech, Signal Processing, vol. ASSP-35, pp.927 -936 1987

7.     Serebryakov  G. “Direction-of-arrival estimation of correlated sources by adaptive beamforming” // IEEE Trans SP, vol.SP-43, pp.2782-2787, 1995.  

8.     Serebryakov G.V., Tiraspolsky S.A., High resolution capability of adaptive antenna arrays for communication systems // Journal of Radioelectronics: electronic journal. 2002. N7. URL: http://jre.cplire.ru/jre/jul02/1/text_e.html

9.       Serebryakov G. “Adaptive array utilizing improved spatial averaging technique” // Electronics Letters, Vol. 36, N. 5, pp. 471-472, 2001.

10.                                                            Montalbano G. and Serebryakov G. “Optimum beamforming performance degradation in the presence of imperfect spatial coherence of wavefronts” // IEEE Transactions on Antennas and Propagation, Vol. 51, No. 5, pp.1030-1039, 2003.

11.                                                            Серебряков  Г., Шин В., “Многоэлементная антенная решетка с дополнительными ограничениями на диаграмму направленности в системах  беспроводной связи” // Радиотехника и электроника, 2006, Т. 51, №12, с. 1431-1435.

12.                                                            Gershman A., Serebryakov G. and  Bohme J. "Constrained Hung-Turner adaptive beam-forming with additional robustness to wideband and moving jammers"// IEEE Trans. AP, vol. 44, no. 3, pp.361 -367 1996.