УДК  537.874.4; 537.874.6

ДИФРАКЦИЯ ПЛОСКОЙ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ НА ДИЭЛЕКТРИЧЕСКОЙ СТУПЕНЬКЕ

А. А. Комаров, В. А. Пермяков

Национальный исследовательский университет «МЭИ»

кафедра Антенных устройств и распространения радиоволн

Получена 24 июля 2013 г.       

 

Аннотация.  Рассмотрена двумерная задача дифракции плоской электромагнитной волны на диэлектрической ступеньке между двумя  однородными полупространствами.  Задача решена численно методом поверхностных интегральных уравнений. Проведен расчет поверхностных токов  и ЭПР  для ступенек различного профиля высотой 30 длин волн и  среды с диэлектрической проницаемостью 3-i0,018.  Расчетные удельные ЭПР сопоставлены с экспериментальными для целей типа льдин и айсбергов.    

Ключевые слова: дифракция, плоская электромагнитная волна,  метод поверхностных интегральных уравнений, диэлектрическая ступенька, ЭПР льдины.   

Abstract:  The 2-D problem of diffraction of a plane electromagnetic wave by a dielectric step between two homogeneous half-spaces is considered. The problem is numerically solved using the method of surface integral equations. Equivalent surface currents and scattering cross-sections for various shapes of the dielectric step with a height of 30 wavelengths and a relative permittivity of 3-i0,018 are calculated. The calculated scattering cross-sections are compared with experimental data for the sea ice and icebergs.  

Keywords: diffraction, plane electromagnetic wave, surface integral equations method, dielectric step, scattering cross-section of the ice field.

 

Введение

Диэлектрическая ступенька (ДС) может рассматриваться как регулярная модель многих прикладных задач электродинамики. При анализе результатов локационного мониторинга ледовой обстановки представляется  полезным изучение зависимости ЭПР льдин от их геометрических характеристик. При этом  возникает проблема расчёта электромагнитного поля, отражённого от льдин. При построении алгоритмов расчета  распространения радиоволн в городе фрагменты домов могут быть аппроксимированы ДС. Родственные  задачи дифракции возникают при анализе прохождения электромагнитных волн через нерегулярности диэлектрических волноводов.  В этих случаях для  расчета электромагнитных полей необходимо решение эталонной задачи дифракции электромагнитных волн на ДС.

Эталонная задача формулируется следующим образом.  Рассматривается дифракция плоской монохроматической электромагнитной волны, падающей под углом к ребру ДС. Необходимо найти структуру электромагнитного поля, рассеянного ступенькой, на произвольных расстояниях от ступеньки.

В статье  проводится анализ дифракции плоской электромагнитной волны на ДС на основе численного решения методом поверхностных интегральных уравнений (ПИУ) аналогично  [1-3]. Ограничимся случаем нормального падения плоской электромагнитной волны на ребро ДС, диэлектрическую  проницаемость среды  примем равной ε = 3 – i0,0018, что соответствует параметрам морского льда на длине волны в свободном пространстве λ=3см [4,5], а также близко к характеристикам строительных материалов [6].

Основное внимание сосредоточим на исследовании амплитудно-фазовых характеристик поверхностных токов и ЭПР рассеивателя. Полученные результаты с практической точки зрения могут быть полезны для оценки рассеяния электромагнитных волн ледовыми полями, фрагментами зданий, нерегулярностями диэлектрических волноводов.

Методика численного решения 

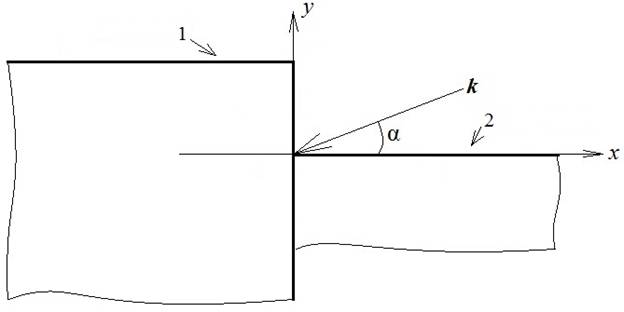
Постановка задачи дифракции плоской электромагнитной волны на диэлектрической ступеньке дана на рис.1.

 

а) 1 – край льдины; 2 – поверхность моря

 

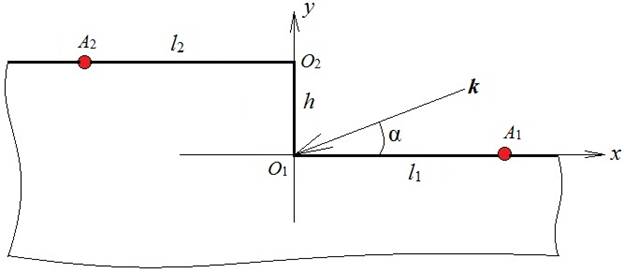
б)

Рис.1. а) Модель края льдины в воде.
б) Поперечное сечение диэлектрической  ступеньки.

 

         Реалистичная модель края  льдины в воде (рис.1а) в нашей постановке заменяется более простой моделью (рис. 1б),  в которой параметры морской воды считаются равными параметрам льда и нижнее полупространство однородно. Такое приближение является оправданным, поскольку мы рассматриваем скользящие углы падения, при которых коэффициенты отражения плоской электромагнитной волны от горизонтальных поверхностей льда и моря близки  по модулю к 1.       

Согласно методу ПИУ  для полубесконечных структур [1-3] бесконечный контур интегрирования в задаче дифракции на ступеньке разбивается точками A₁ и A₂ на три части:  два полубесконечных контура, идущих на бесконечность от точек A₁ и A₂, и контур конечной длины между точками A₁ и A₂ (рис.1).

При численном решении для поверхностных токов используется введенное П.Я.Уфимцевым понятие о равномерных и неравномерных  частях токов [7]. При этом  положения точек, выделяющих полубесконечные контуры, выбираются таким образом, чтобы на этих контурах можно было пренебречь неравномерными токами. Равномерные токи на плоских гранях определяются в приближении геометрической оптики через параметры падающей плоской волны и коэффициенты Френеля. В результате исходное ИУ по бесконечному контуру сводится к ИУ для полных токов на конечном контуре A₁A₂. Для конкретного случая ступеньки, изображенной на рис.1, участки A₁О₁ и О₂A₂  полагались плоскими, а форма контура О₁О₂ варьировалась.

   Результатом  решения ИУ являлись полные токи   на контуре конечной длины. Дифракционные поля вычислялись с использованием теоремы эквивалентности, как асимптотические представления цилиндрической волны  в дальней зоне [2].

Расчёты проводились для Е- и Н-поляризаций (вектор электрического/магнитного поля параллелен ребру ступеньки) падающего поля. Ребра ступеньки при численном решении сглаживались окружностью малого радиуса (в нормированных единицах ρ = kR= 0,1, k=2π/λ, R – радиус скругления).   

Анализ результатов расчетов для нормального падения плоской волны  на диэлектрическую ступеньку

Конкретные расчеты были проведены для ступенек  различной формы. Длины горизонтальных участков l₁, l₂ и высота  ступеньки h были взяты равными по 30λ, так что общая длина контура интегрирования составляла для вертикальной ступеньки  не менее 90λ (рис.1).  

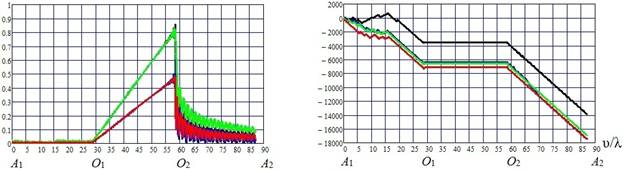
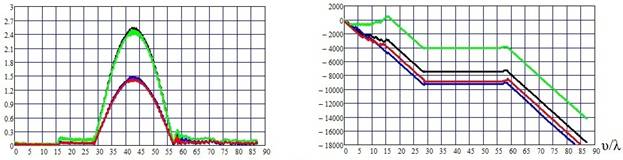
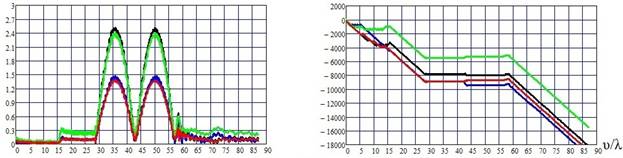
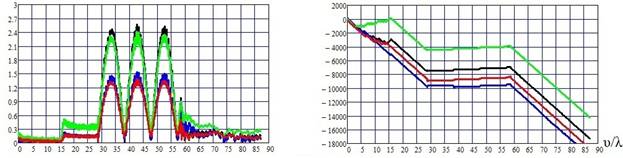
На рис. 2а) - 2г) приведены распределения амплитуд и фаз поверхностных токов по контуру A₁A₂ поперечного сечения ступеньки при разных углах падения α.

 

а)

б)

в)

г)

Рис.2. Амплитуды и фазы поверхностных токов: а) α = 0,1^о; б) α = 1^о; в) α = 2^о; г) α = 3^{о .} Длина контура v отсчитывается от  точки A₁ к A₂.

 

На всех рисунках, относящихся к поверхностным токам, использованы следующие обозначения: для Е-поляризации черным цветом показана составляющая электрического тока , синим – составляющая магнитного тока ; для Н-поляризации зелёным цветом – , красным – .

Из рис. 2а) - 2г) следует, что характер  поверхностных токов качественно различается на трех плоских  поверхностях диэлектрической структуры. 

При весьма малом угле падения (рис.2а) токи на ближней к источнику горизонтальной части структуры практически равны нулю. На дальней  от источника   горизонтальной части структуры формируются сильно осциллирующие неравномерные токи. Наконец, на торце ступеньки  токи линейно падают от максимальных значений на верхней части  ступеньки до нуля  на нижней части. Последнее означает, что источником тока является верхнее ребро ступеньки, возбуждаемое падающей плоской волной, а сумма падающего и отраженного (в приближении геометрической оптики) полей на  торце  близка к нулю.  

Незначительное, на первый взгляд, увеличение угла падения до 1 градуса приводит к качественному изменению поведения токов на торце ступеньки (рис.2.б). На нем формируется стоячая волна  с одним полупериодом.    Физически такую структуру токов можно объяснить тем, что наклонно падающая на торец волна бежит вдоль торца ступеньки с  фазовой скоростью  , что соответствует эквивалентной длине волны  При этом высота торца ступеньки близка к резонансной .

При кратном увеличении угла падения волны соответственно на торце возникает стоячая волна с двумя (рис.2.в), тремя (рис.2.г) полупериодами и так далее. Стоячие волны на торце формируются суперпозицией падающей и отраженной волн в уголковом отражателе, образованном нижней горизонтальной плоскостью и торцом.  С увеличением угла падения появляется незначительный отраженный ток  на ближней к источнику волны горизонтальной части диэлектрической структуры и ослабевает ток на удаленной от источника горизонтальной части структуры. 

По фазовым характеристикам токов  легко определить фазовую скорость волн, бегущих вдоль отдельных частей структуры. На удаленной от источника горизонтальной части структуры существует бегущая волна  с фазовой скоростью, близкой к скорости света в вакууме. На торце ступеньки фазовая скорость близка к бесконечности (рис.2.а),  а с увеличением угла падения уменьшается,  причем по углу наклона фазы видно, что волна бежит от верхнего ребра ступеньки вниз.  

 Важным параметром, характеризующим радиолокационные свойства объекта, является эффективная площадь рассеяния (ЭПР) σ. Для объекта большой площади принято определять  удельную ЭПР (УЭПР), как ЭПР, отнесённую к единице его площади.

Для волн Е- и Н-поляризаций   УЭПР определяется формулами

 

 

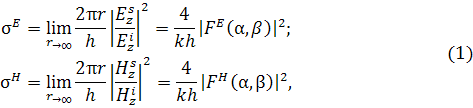
где ,   –  угловые характеристики рассеяния,α – угол падения, β – угол наблюдения, r – расстояние от начала координат до точки наблюдения.

 

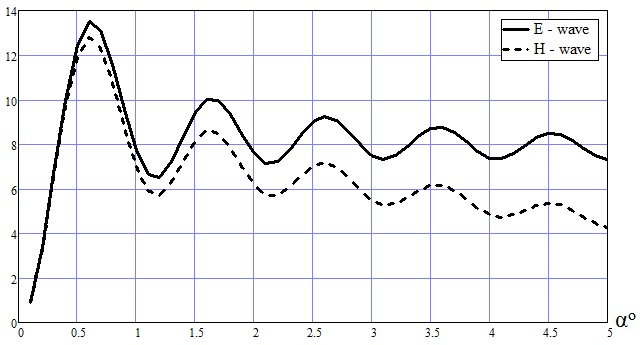
Рис.3. Зависимость УЭПР от угла падения

 

На рис.3 показана зависимость УЭПР от угла падения α для ступеньки с плоским торцом при обратном рассеянии (α=β).

Из рис. 3 следует, что при близком к нулевому углу падения (α = 0,1^o) амплитуда поля для обратного рассеяния мала и не зависит от поляризации падающего поля. Далее с увеличением угла падения (в секторе малых углов  до 5^о)  амплитуда поля незначительно колеблется относительно медленно убывающего среднего  значения в случае Е-поляризации.  В случае Н-поляризации убывание амплитуды обратного рассеяния в среднем идет быстрее, чем для Е-поляризации.

Также были проведены расчёты УЭПР для разных видов ступенек.

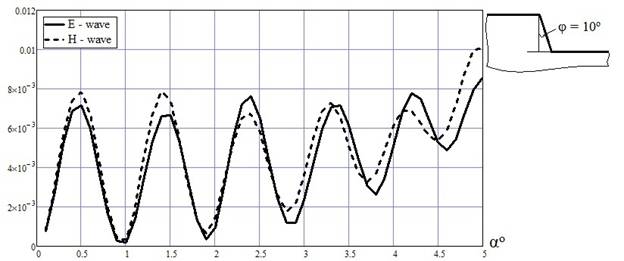
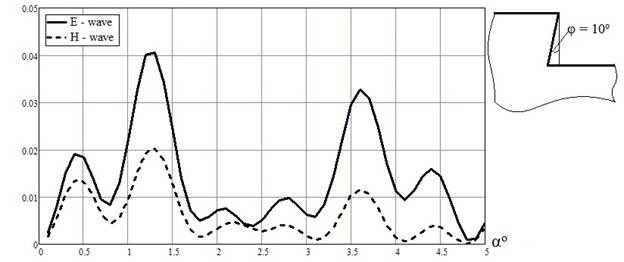
На рис. 4 показаны результаты расчётов УЭПР ступенек с разными углами наклонов торцевой части.

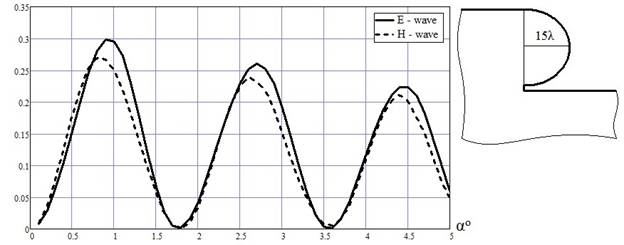
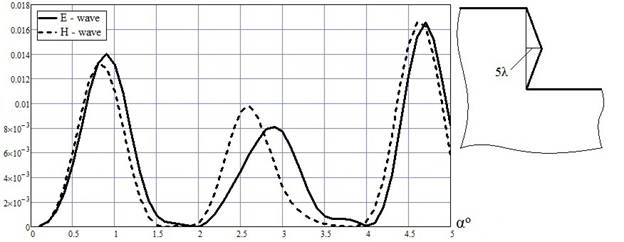
Результаты расчётов УЭПР при наличии крупномасштабной неоднородности на торце ступеньки показаны на рис.5.

Из рис. 4, 5 видно, что наличие крупномасштабной неоднородности на торце ступеньки приводит к следующим отличиям: 1) амплитуда поля обратного рассеяния для ступеньки с нерегулярностью существенно меньше (более чем в 10 раз), чем для идеально гладкой ступеньки; 2)  амплитуда поля обратного рассеяния слабо зависит от поляризации падающего поля.

 

а)

б)

Рис.4 Зависимость УЭПР от угла падения для ступенек с разными углами наклонов торца.

а)

б)

Рис. 5 Зависимость УЭПР от угла падения при наличии крупномасштабной неоднородности

 

На рис.6 приведены результаты расчётов при наличии  неоднородностей малой, по сравнению с длиной волны, высоты на вертикальной части ступеньки.

 

 

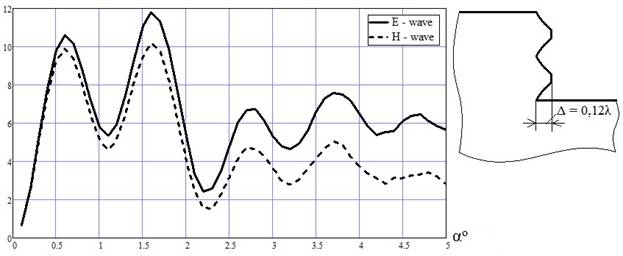
Рис. 6. Зависимость УЭПР от угла падения при наличии неоднородностей малой высоты

 

Зависимости, представленные на рис. 6, по характеру изменения похожи на аналогичные расчёты для идеально гладкой ступеньки (рис. 3): при близком к нулевому углу падения амплитуда поля для обратного рассеяния мала и не зависит от поляризации падающего поля; с увеличением угла падения амплитуда поля приобретает колебательный характер; в случае  Н-поляризации убывание амплитуды обратного рассеяния в среднем идет быстрее, чем для Е-поляризации.

         Из проведенных расчётов следует, что изменение параметров неоднородности приводит к значительным колебаниям УЭПР. 

Обсудим качественную физическую трактовку полученных результатов.  Оценим предельные значения УЭПР в приближении физической оптики. Заменим диэлектрическую ступеньку (рис.1) диэлектрическим брусом той же высоты h, что и ступенька.  При условии  h >> λ в приближении физической оптики   ЭПР бруса при падении плоской волны на его торец определим по формуле

 

σ=σ₀│Г│²,                                                       (2)

 

где  σ₀ – ЭПР  идеально проводящей полосы, закрывающей торец бруса,  Г – коэффициент отражения Френеля по полю от диэлектрического полупространства. Система координат та же, что на рис. 1,  ширина полосы равна h.

ЭПР    идеально проводящей полосы найдем в приближении физической оптики , используя решение задачи дифракции плоской волны на полосе [10].   Для плоской волны Е поляризации амплитуда отраженного электрического  поля определяется формулой (используется временной множитель exp(iωt)) [10]

 

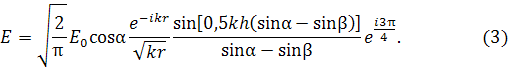
        Определив ЭПР на единицу ширины полосы, как

 

 

получим

 

 

 

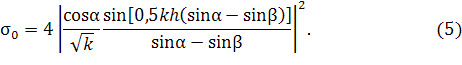
В результате с учетом (2)- (5) имеем следующее выражение для УЭПР

 

 

 

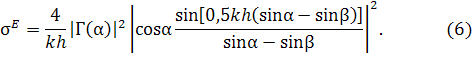
В случае Н поляризации формула для УЭПР отличается от (6) только тем, что соsα  в модуле последнего  сомножителя заменяется на  cosβ. 

В малоугловом приближении  (α<<1, β<<1)  можно положить соsα= cosβ=1 и независимо от поляризации  определить УЭПР  формулой

 

                                           

 

 

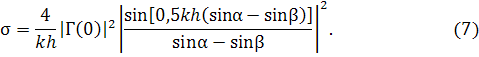
В случае обратного рассеяния  (α=β)  получим

 

                                                    (8)    

     

Формула (8) трактуется следующим образом: множитель kh   можно трактовать, как коэффициент направленного действия ступеньки, рассматриваемой, как апертура источника вторичного излучения, множитель       представляет собой энергетический коэффициент отражения плоской волны  от диэлектрического полупространства.  

Проведем  конкретную оценку УЭПР  в приближении физической оптики для данных, использованных в расчете по методу ПИУ: ε=3, h =30λ.   Получим σ = 13,5, что отлично согласуется с расчетом УЭПР для первого максимума на  рис. 3. Это максимально возможное значение УЭПР.       В том случае, когда  профиль ступеньки  нерегулярный, УЭПР будет меньше полученного выше максимально возможного.  Так, когда поверхность ступеньки представляет собой мелкомасштабные нерегулярности и имеет место некогерентное рассеяние, коэффициент направленного действия апертуры будет порядка единицы  и УЭПР по порядку величины должно быть близко к значению    Таким образом, согласно простым оценкам в зависимости от профиля ступеньки максимальные УЭПР могут варьироваться в широких пределах примерно  от 13,5 до 0.07. 

Как следует из численных результатов рис. 3 - 6,  максимальные значения УЭПР меняются в пределах от 13,5 до 0,017. Сравнение  численных результатов с проведенными выше оценками объясняет существенные колебания  УЭПР c изменением профиля  края льдины, что важно для понимания сложности радиолокационного обнаружения льдов в реальных условиях.  Следует отметить, что ранее вопрос о рассеянии электромагнитных волн кромкой льда теоретически не рассматривался, за исключением  нашей работы [9].

Известные экспериментальные данные  для  льдин и айсбергов  при радиолокации при малых углах места дают УЭПР 0,05…1,2  [4] и 0,06-0,08 [5]. Полученные нами численные результаты согласуются с экспериментальными данными по порядку величины  при учете нерегулярности края льдины. 

         Исследование выполнено при финансовой поддержке РФФИ в рамках научных проектов  № 13-08-00735а  и № 11-08-01249а.

  

Литература

1.     Васильев Е.Н., Солодухов В.В. Метод интегральных уравнений в задачах дифракции на полубесконечных диэлектрических структурах. Препринт № 25(397) . – М.:  ИРЭ АН СССР, 1984 .

2.     Васильев Е.Н., Солодухов В.В. О дифракционных коэффициентах для диэлектрического клина. //В сб. Теория дифракции и распространения волн. Т.1. VI Всесоюзный симпозиум по дифракции и распространению волн.  1973.  С. 238-242.

3.     Васильев Е.Н., Солодухов В.В. Дифракция электромагнитных волн на диэлектрическом клине. //Известия ВУЗов, Радиофизика, 1974, т. 17, № 10, с. 1518-1528.

4.     Винокуров В.И., Генкин В.А., Калиниченко С.П. и др . Морская радиолокация. /Под ред. д.т.н., профессора В.И. Винокурова, -Л.: Судостроение, 1986, -256 с. 

5.     S. S. Haykin, E.O.Lewis, R.K.Raney, J.R.Rossister. Remote sensing of sea ice and icebergs. John Wiley & Sons Inc. 1994. -687 pp.

6.     Лещанский Ю.И., Лебедева Г.Н., Ульянычев Н.В. Электрические параметры кирпича, цемента и древесины в диапазоне метровых-сантиметровых радиоволн // Изв. вузов. Сер. Радиофизика, 1982. Деп. ВИНИТИ № 4772-82.

7.     Уфимцев П.Я. Метод краевых волн в физической теории дифракции. – М.: Сов. Радио, 1962, -  243 с.

8.     Потехин А.И. Некоторые задачи дифракции электромагнитных волн. –М.: Советское радио, 1948, -1 34 с.

9.     Комаров А.А., Пермяков В.А.  Дифракция плоской электромагнитной волны на диэлектрической ступеньке. // XXIII Всероссийская научная конференция «Распространение радиоволн», Йошкар-Ола, 23-26 мая 2011 г., тезисы докладов, МарГТУ,  т. 3, с. 368-371, 2011.