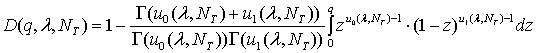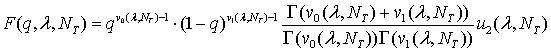УДК 621.37+621.391:519.218.5
ХАРАКТЕРИСТИКИ ОБНАРУЖЕНИЯ ПЕРИОДИЧЕСКОГО ПОТОКА С НЕЗАВИСИМОЙ ДЕЦИМАЦИЕЙ В СУПЕРПОЗИЦИИ С ПРОСТЕЙШИМ ПОТОКОМ
Ф. В. Голик
Новгородский государственный университет им. Ярослава Мудрого
Статья получена 29 июня 2015 г., после доработки – 10 августа 2015 г.
Аннотация. Рассматривается суперпозиция потока Пуассона и периодического потока с независимой равновероятной децимацией и неизвестным периодом следования точек. Методом компьютерного моделирования найдены характеристики обнаружения периодического потока по критерию идеального наблюдателя.
Ключевые слова: случайный поток, суперпозиция потоков, критерий идеального наблюдателя, вероятность обнаружения, вероятность ложной тревоги, рабочие характеристики обнаружения.
Abstract. The article is devoted to the superposition of Poisson arrival and periodic stream with independent equally probable decimation and unknown period of following points. Characteristics of the periodic stream are found by the method of computer simulation in accordance with the ideal observer criterion.
Keywords: random stream, superposition of streams, ideal observer criterion, acquisition probability, false-alarm probability, detection performances.
Введение. Постановка задачи
По определению случайный поток представляет собой множество точек на числовой оси. Координаты точек временного потока упорядочены по возрастанию и интерпретируются как моменты времени, в которые возникают некоторые однородные события. В теории массового обслуживания [1-4] и др. в качестве однородных событий рассматривают появление требования на обслуживание. В теории надежности [5] – отказ объекта. В прикладных задачах радиолокации и связи под событиями понимаются, например, факты обнаружения сигнала [6,7], а так же пересечений постоянного уровня случайным процессом, появление выброса случайного процесса [8-12].
Любая фиксированная последовательность моментов событий называется реализацией потока. В настоящей работе рассматриваются реализации децимированного периодического потока, простейшего (пуассоновского) потока и их суперпозиция.
Реализация
детерминированного периодического потока задается тремя параметрами: эпоха 
- момент появления первой точки 
; период следования точек 
; количество точек в потоке (размер
потока) 
. Обычно полагают, что эпоха равномерно распределена на интервале 
с плотностью вероятностей 
. Формальная запись реализации
периодического потока имеет вид:
(1)
В случае периодического
потока со случайной децимацией кроме этих параметров задается закон «прореживания»
точек потока. В настоящей работе рассматривается случай равновероятной
независимой децимации. Каждая точка потока 
может
быть потеряна с вероятностью q и сохранена с вероятностью
. Тогда реализации децимированного потока
соответствует вектор
. (2)
Условие независимости
децимации выполняется, если 
.
Реализация простейшего потока с экспоненциальным распределением интервалов между точками задается соотношением:
(3)
где 
- плотность распределения случайной
величины x, а 
- интенсивность потока.
Суперпозиция потоков 
образуется в результате их временного перекрытия
и формально задается как
,
(4)
где оператор 
возвращает массив, образованный размещением
A, B, C, ... сверху вниз; A, B, C, ... — массивы с одинаковым числом столбцов;
оператор 
возвращает вектор со значениями
из v, упорядоченными по возрастанию.
На рис. 1 изображены случайные реализации децимированного периодического потока, простейшего потока и их суперпозиция.
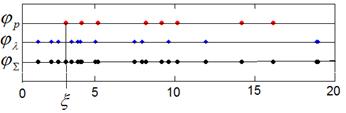
Рис. 1. Случайные реализации потоков. Параметры: T=1, q=0.4, L=5.1T, NT=15, λ=0.7.
При анализе случайных потоков в рамках теории массового обслуживания и теории надежности основное внимание уделяется оценке законов распределения интервалов между точками потока, распределению числа точек, исследованию фундаментальных свойств потоков. При решении задач радиотехнического профиля исследуют распределения интервалов, спектральные и корреляционные характеристики [9,13-15].
В прикладных областях, таких как радиотехника, экономика, финансы, медицина и др., возникает задача обнаружения периодических потоков или выявление периодичностей в суперпозиции потоков. В радиотехнике это позволяет обнаружить детерминированную составляющую – сигнал, а в финансово-экономической области прогнозировать время появления очередного события.
Цель настоящей работы состоит в разработке процедуры обнаружения децимированного периодического потока с неизвестным периодом в суперпозиции с простейшим потоком и нахождении вероятностных характеристик обнаружения.
В
терминах теории радионаблюдения и пассивной радиолокации суперпозицию периодического
и простейшего потоков можно рассматривать как последовательность моментов
принятия решения об обнаружении одиночного сигнала. При этом точкам
периодического потока 
соответствуют моменты
правильного обнаружения. Точкам потока 
-
моменты ложного обнаружения импульса хаотической импульсной помехи (ХИП). Таким
образом, поставленная задача в частном случае сводится к обнаружению пачки
радиоимпульсов с прямоугольной огибающей и неизвестным периодом следования на
фоне ХИП. При этом вероятность пропуска обнаружения одиночного сигнала интерпретируется
как вероятности децимации 
, а
вероятность правильного обнаружения равна 
.
Процедура обнаружения периодического потока
В [16] найдены вероятностные характеристики обнаружения периодического потока точек с децимацией. Задача сводилась к оценке периодичности исследуемого процесса, процедура обнаружения которой предложена в [17] и базируется на поиске максимума функции
,
(5)
где 
- момент появления 
-й точки потока.
Полученные в [16, 17] результаты справедливы для одиночных потоков. В этом случае возможна компенсация эпохи путем совмещения начала отсчета времени с моментом появления первой точки потока.
В нашем случае такой метод компенсации сопряжен с необходимостью оценки эпохи, поскольку точки периодического и простейшего потоков в суперпозиции неразличимы, а по определению эпоха равна координате первой точки периодического потока, которая неизвестна.
Рассмотрим
метод компенсации эпохи, базирующийся на вычислении спектральной функции (СФ) потока
-функций 
,
сопряженного с суперпозицией 
.
При
отсутствии децимации (
) поток -функций записывается соотношением:
где
- размер потока ; 
размеры
периодического и простейшего потоков соответственно.
Косинус-
и синус-преобразования Фурье потока 
равны:
, (6)
(7)
и СФ равна
. (8)
Покажем,
что максимумы СФ при наличии периодического потока находится в окрестностях точек
.
Перепишем выражения (6) и (7):
, (6а)
. (7а)
Тогда
(9)
Воспользовавшись соотношениями [18, 1.341.3] и [18, 1.341.1] получаем:
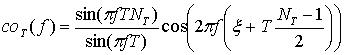, (10)
,
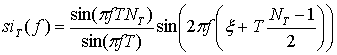(11)
.
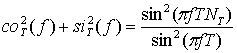(12)
Функция (12) является
доминирующим членом подкоренного выражения (9). Она не зависит от эпохи , неслучайна и принимает максимальные
значения, равные 
, при
Остальные члены подкоренного выражения (9) случайны. Их влияние можно оценить по математическому ожиданию СФ. Учитывая, что аналитическое выражение весьма громоздко (см. [17]) и в нашем случае оно нужно лишь для визуального подтверждения вывода о положении максимума СФ на оси частот, найдем их путем компьютерного моделирования.
По K
=10000 реализациям суперпозиции периодического и простейшего потоков 
, 
рассчитаны СФ 
реализаций потоков
и найдена оценка среднего значения 
. Здесь 
,
, 
,
, 
,
=0.001T.
На рис. 2 построены графики спектральных характеристик для
потока без децимации. Видно, что глобальные максимумы среднего 
и СФ 
случайно
выбранной 
-той реализации потока 
лежат в окрестностях частот, равных 
и 
.
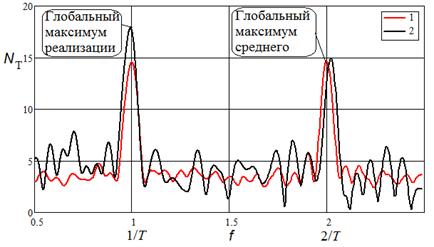
Рис. 2. Спектральные характеристики суперпозиции
периодического потока без децимации и простейшего потока. Параметры парциальных
потоков:
=15, 
=1,
, 
.
1). Среднее значение 
СФ. 2). СФ одной из
случайных реализаций потока .
Рассмотрим ситуацию,
когда в составе суперпозиции содержится децимированный периодический поток 
.
СФ суперпозиции равна:
(9а)
Косинус-преобразование Фурье
потока можно представить в следующем виде:
(13)
где 
- случайный множитель принимающий
значение 1 с вероятностью 
и 0 с вероятностью
децимации 
(см. (2)).
Аналогично синус-преобразование равно
.
(14)
Функции (13) и (14)
случайны. При частотах они соответственно
равны:
,
(15)
. (16)
Тогда
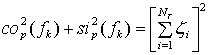(17)
Сумма 
распределена по закону Бернулли.
Математическое ожидание функции (16) равно
(18)
При 
,
что совпадает со значением функции (12) при
Очевидно, что с
увеличением вероятности 
потери точки
периодического потока влияние периодической составляющей убывает.
На рис. 3 приведены спектральные характеристики суперпозиции с децимированным периодическим потоком.
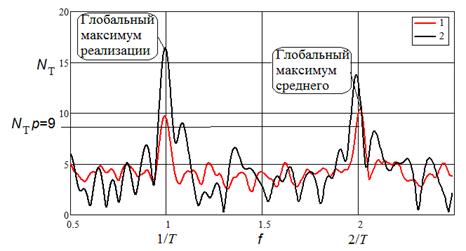
Рис. 3. Спектральные
характеристики суперпозиции периодического потока с децимацией и простейшего
потока.
Параметры парциальных потоков: =15,
=1, 
,
.
1). Среднее значение СФ. 2). СФ одной из случайных реализаций
потока .
Из анализа графиков рис.
2 и 3 можно сделать вывод, что глобальные максимумы как среднего значения , так и СФ конкретной реализации потока преимущественно
лежат в окрестности одной из точек 
. Следовательно,
для обнаружения периодического потока нужно найти глобальный максимум СФ и
сравнить его с некоторым порогом 
. Решение об
обнаружении принимается, если 
, 
, 
.
Для нахождения
оптимального порога обнаружения необходимо знать законы распределения
глобальных максимумов СФ потоков и 
. Учитывая, что СФ зависит, хотя и
нелинейно, от большого числа случайных величин, а доминирующая составляющая распределена
по закону Бернулли[1],
достаточно велика вероятность, что распределение глобальных максимумов СФ может
аппроксимироваться нормальным законом.
С целью подтверждения этого
предположения проверялась гипотеза о нормальности распределения по критерию
омега-квадрат при следующих комбинациях параметров потоков: 
, 
,
={10, 15, 20, 30, 40. 50}. Для каждой
комбинации объем выборки 
составлял 10000.
Учитывая, что объем весьма велик, можно считать, что генеральные среднее и дисперсия
незначимо отличаются от выборочных. Следовательно, допустимо применение простой
гипотезы, при которой порядок квантили распределения омега-квадрат рассчитывается
по формуле (32).
Оказалось, что при 
> 5 и 
>5, где 
- длина
интервала наблюдения, порядок квантиля 
<
0,95, т. е. гипотеза не отклоняется при уровне значимости 
>0,05. Следовательно, аппроксимация
нормальным распределением допустима.
Найдем оптимальный порог обнаружения по критерию идеального наблюдателя.
Вероятность суммарной ошибки равна
,
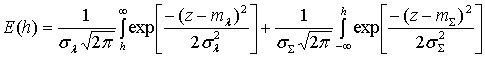где 
математическое ожидание и
среднеквадратическое отклонение глобальных максимумов СФ потока ; 
-
математическое ожидание и среднеквадратическое отклонение глобальных максимумов
СФ суперпозиции .
Оптимальный порог равен корню уравнения
.
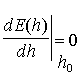Корень, соответствующий
минимуму 
равен
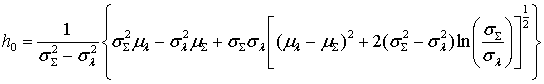. (19)
Имитационная модель
Задача оценки вероятностных характеристик обнаружения решена методом компьютерного моделирования в программе Mathcad. Модель имитирует процессы формирования периодического и простейшего потоков, их суперпозиции. Вычисляет СФ для каждой реализации потоков. Находит глобальные максимумы СФ в заданном интервале частот. По ансамблю реализаций оцениваются дисперсия и математическое ожидание максимумов СФ для суперпозиции потоков и для простейшего потока, а также выполняются вычисления, необходимые для проверки гипотезы о законе распределения максимумов. На основании этих данных рассчитывается оптимальный порог обнаружения и формируется статистика результата обнаружения для каждой реализации.
Рассмотрим перечисленные процедуры подробней.
Условные обозначения исходных данных:
– объем выборки;
- размер периодического потока
(количество точек);
- период следования точек периодического
потока[2];
- максимальное значение эпохи;
- интервал возможных значений периодов[3];
- шаг дискретизации по времени;
- максимально допустимое отклонение
оценки периода от истинного;
- вероятность децимации;
- интенсивность простейшего потока.
1. Формирование потоков.
Периодический поток .
, 
,
;
(20)
где 
[4]
- й вектор матрицы децимирующих коэффициентов,
[5]
- вектор эпох - случайных величин с равномерным распределениям в интервале 
.
Простейший поток .
, 
,
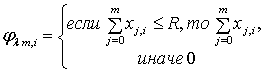(21)
где 
[6]
- количество точек потока Пуассона, которые с вероятностью 
могут появиться на интервале
наблюдения длиной 
; 
[7]
- -й вектор 
случайных
экспоненциально распределенных с параметром .
Суперпозиция потоков .
В отличие от (4) при численных
расчетах можно не выполнять сортировку, поскольку СФ потока не зависит от
номера точки. Тогда поток суперпозиции есть матрица размера 
:
.
(22)
2. Спектральные
функции потоков и .
СФ суперпозиции :
, ,
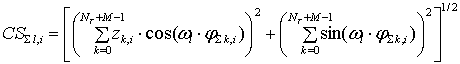, (23)
где 
, 
;
, 
.
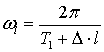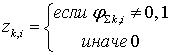СФ простейшего потока
:
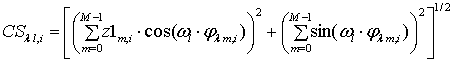,,, (24)
где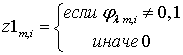 
, .
3.
Числовые характеристики глобальных максимумов спектральных функций 
.
Суперпозиция :
Вектор максимумов СФ потока
:
, .
(25)
Среднее значение максимумов
СФ потока :
[8].
(26)
Среднеквадратическое
отклонение максимумов СФ потока :
[9].
(27)
Простейший поток :
Вектор максимумов СФ потока
:
, .
(28)
Среднее значение
максимумов СФ потока:
.
(29)
Среднеквадратическое
отклонение максимумов СФ потока:
.
(30)
4.
Проверка гипотезы о нормальности распределения глобальных максимумов
спектральных функций потоков и .
При проверке гипотезы по критерию омега-квадрат статистика критерия вычисляется по формуле:
,
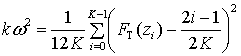(31)
[10]
- функция нормального распределения.
При проверке гипотезы о
распределении максимумов СФ потока 
, 
,
. Для потока :
, 
,
.
Порядок квантиля определяется
по приближенной формуле, полученной путем аппроксимации функции распределения
статистики критерия 
[19, табл. 6.4а]:
.
(32)
5. Оценка вероятности правильного обнаружения периодического сигнала.
Решение об обнаружении
принимается, если частота 
, при которой 
, 
,
находится в пределах 
и максимум СФ превышает порог 
. То есть вероятность правильного
обнаружения равна:
(33)
Оценка вероятности равна
,
(34)
где
[11],
,
, 
[12];
,
.
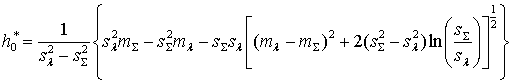(35)
6. Оценка вероятности ложного обнаружения периодического сигнала.
Ложное обнаружение
наступает, когда максимум СФ потока превышает
порог :
.
(36)
Оценка вероятности:
где 
.
Результаты моделирования
Параметры модели.
Объем ансамбля реализаций (объем выборки) K=10 000.
Размер периодического
потока ={10; 15; 20; 30; 40; 50}.
Период следования точек потока T=1.
Максимальное значение
эпохи =5.
Шаг дискретизации по
времени 
.
Максимально допустимое
отклонение оценки периода от истинного значения =2.
Интервал возможных
значений периодов 
.
Вероятность децимации
точки периодического потока ={0; 0,1;
0,2;…0,9}.
Интенсивность простейшего
потока 
.
Отметим, что период T следования точек периодического потока и интенсивность простейшего потока заданы как
безразмерные величины, что затрудняет интерпретацию результатов моделирования.
Это затруднение можно обойти, если степень влияния помехи характеризовать не ее
интенсивностью , а средним числом
точек 
потока, появляющихся на
интервале длиной .
Учитывая, что при моделировании период принят равным 1, то получаем, что
среднее число точек потока численно
равно интенсивности .
Вероятность правильного обнаружения.
Для указанных выше
параметров модели по формуле (34) найдены оценки вероятности правильного
обнаружения. В результате анализа массива экспериментальных данных оказалось,
что зависимость вероятности обнаружения от 
хорошо
аппроксимируется[13]
интегральной функцией бэта-распределения [20]:
где 
, 
.
Оценки
коэффициентов 
и 
приведены
в табл. 1.
Таблица 1
|
Интенсивность помехи |
|
|
||
|
|
|
|
|
|
|
0,1 |
-0,494 |
0,317 |
1,389 |
0,027 |
|
0,2 |
-1,157 |
0,296 |
1,324 |
0,041 |
|
0,3 |
-0,744 |
0,247 |
1,568 |
0,037 |
|
0,4 |
-0,970 |
0,228 |
1,426 |
0,044 |
|
0,5 |
-1,088 |
0,212 |
1,301 |
0,049 |
|
0,7 |
-0,975 |
0,167 |
1,266 |
0,046 |
Вероятность ложного обнаружения.
Оценки вероятности
вычислялись по формуле (37). Зависимость вероятности ложного обнаружения от надежно[14]
аппроксимируется трехпараметрической функцией
где 
, 
,
Оценки коэффициентов 
приведены в табл. 2.
Таблица 2
|
Интенсивность помехи |
|
|
|
|||
|
|
|
|
|
|
|
|
|
0,1 |
1,292 |
0,319 |
1,985 |
0,012 |
0,032 |
-4.441 10-4 |
|
0,2 |
-0,519 |
0,336 |
1,644 |
0,033 |
0,046 |
-7.274 10-4 |
|
0,3 |
-1,491 |
0,349 |
1,052 |
0,068 |
0,054 |
-9.227 10-4 |
|
0,4 |
-0,541 |
0,248 |
1,594 |
0,033 |
0,056 |
-8.442 10-4 |
|
0,5 |
-0,407 |
0,215 |
1,425 |
0,036 |
0,058 |
-8.122 10-4 |
|
0,7 |
-0,267 |
0,166 |
1,696 |
0,023 |
0,061 |
-7.282 10-4 |
Вероятность суммарной ошибки:
.
Рабочие характеристики.
Рабочие характеристики
правильного обнаружения, ложного обнаружения и суммарной вероятности ошибки
рассчитываются путем численного решения уравнений 
,
, 
соответственно,
где 
заданные значения вероятностей.
Графическое представление вероятностных характеристик.
С целью иллюстрации найденных
зависимостей построены графики вероятностей обнаружения, ложной тревоги и
суммарной ошибки для ограниченного набора параметров [15]
(рис. 4-6). Графики рабочих характеристик приведены на рис. 7-9.
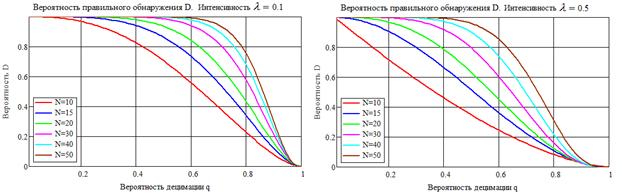
Рис. 4. Зависимость вероятности правильного обнаружения периодического потока от вероятности децимации.
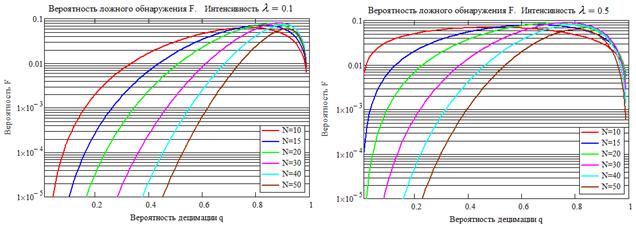
Рис. 5. Зависимость вероятности ложного обнаружения периодического потока от вероятности децимации
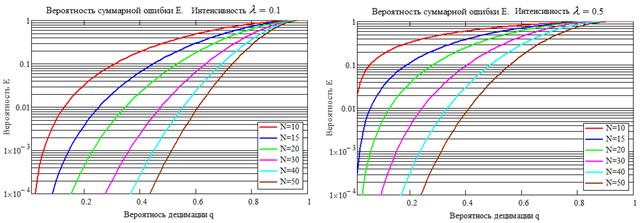
Рис. 6. Зависимость суммарной вероятности ошибки обнаружения периодического потока от вероятности децимации.
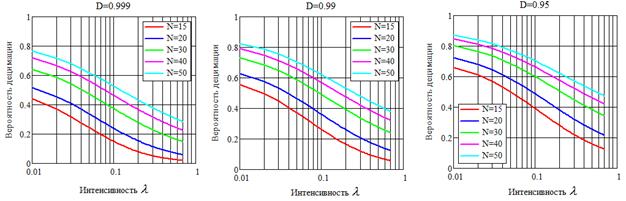
Рис. 7. Рабочие характеристики обнаружения периодического потока.
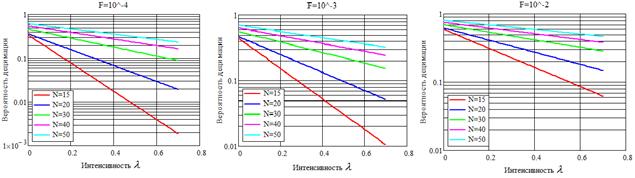
Рис. 8. Рабочие характеристики ложного обнаружения периодического потока.
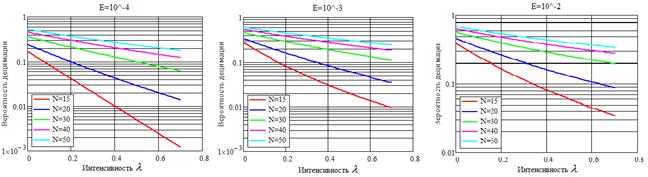
Рис. 9. Рабочие характеристики вероятности ошибки обнаружения периодического потока.
Заключение
Получены достоверные оценки вероятностных характеристик обнаружения периодического потока в суперпозиции с простейшим потоком.
Аппроксимирующие
функции (38)
и (39)
найдены по репрезентативным выборкам большого объема и могут быть использованы
при расчете вероятностных характеристик в достаточно широком диапазоне значений
параметров 
.
Подробное описание имитационной модели позволяет применять ее при расчете вероятностные характеристики обнаружения при любых допустимых параметрах потоков.
Предложенная процедура обнаружения периодических потоков может найти применение в системах пассивной радиолокации и системах радионаблюдения, а также в прикладных задачах, связанных с исследованием свойств случайных потоков.
Литература
1. Риордан Дж. Вероятностные системы обслуживания. - М.: Связь, 1966. - 184 с.: ил.
2. Саати Т. Л. Элементы теории массового обслуживания и ее приложения. - М.: Сов. радио. 1971, - 520 с.: ил.
3. Кокс А., Льюис П. Статистический анализ последовательности событий. – М.: Мир, 1969. – 312 с.: ил.
4. Калашников В. В., Рачев С. Т. Математические методы построения стохастических моделей обслуживания. – М.: Наука, 1988. – 312 с.: ил
5. Надежность технических систем: Справочник / Ю. К. Беляев, В. А. Богатырев, В. В. Болотин и др.; Под ред. И. А. Ушакова. – М.: Радио и связь, 1985. – 606 с., ил.
6. Большаков И. А. Статистические проблемы выделения сигналов из шума. – М.: Сов. радио, 1969. – 464 с., ил.
7. Большаков И. А., Ракошиц В. С. Прикладная теория случайных потоков. – М.: Сов. радио, 1978. – 248 с., ил.
8. Тихонов В. И. Статистическая радиотехника. – М.: Сов. радио, 1966. – 678 с.: ил.
9. Тихонов В. И., Харисов В. Н, Статистический анализ и синтез радиотехнических устройств и систем: Учебное пособие для вузов. – М.: Радио и связь, 1991. – 608 с.: ил.
10. Тихонов В. И., Хименко В. Н. Выбросы траекторий случайных процессов. М.: Наука, 1987.
11. Фомин Я. А. Теория выбросов случайных процессов. М.: Связь. 1980г. 216 с., ил.
12. Билык М. Г. О потоках пересечений постоянного уровня нестационарными процессами/ Отбор и передача информации, № 48, 1976.
13. Лабунец Л. В. Оценка распределения длительности выбросов одного класса негауссовских случайных процессов. / М.: Радиотехника.- 1986. - № 9. - С. 64-67 .
14. Лабунец Л. В. Распределение длительности выбросов нестационарного нормального процесса. /М.: Радиотехника. - 1985. - № 11. - С. 47-50.
15. Билык М. Г. О некоторых характеристиках пересечений случайных процессов. /Отбор и передача информации, № 59, 1980.
16. Голик Ф. В., Порхунов Е. А. Периодический поток со случайной независимой децимацией. // Журнал радиоэлектроники: электронный журнал. 2008. N 10.URL: http://jre.cplire.ru/jre/oct08/index.html.
17. Голик Ф. В. Обнаружение почти-периодических потоков. // Журнал радиоэлектроники: электронный журнал. 2010. N 6. URL : http://jre.cplire.ru/jre/jun10/index.html.
18. Градштейн И. С., Рыжик И. М.: Таблицы интегралов, сумм, рядов и произведений. М.: Наука, 1971. - 1108 с.: ил.
19. Большев Л. Н., Смирнов Н. В. – М.: Наука. Главная редакция физико-математической литературы, 1983. – 416 с.
20. Случайные процессы в параметрических моделях надежности /Переверзев Е. С. – Киев: Наук. думка, 1987.- 240 с.
[1] Отметим, что согласно теореме Лапласа распределение Бернулли при определенных условиях может аппроксимироваться распределением Гаусса.
[2] В соответствии с постановкой задачи период Т потока неизвестен. При моделировании необходимо его задавать для оценки вероятности ложных обнаружений на частотах, отличных от k/Т.
[3] В реальных условиях интервал [T1, T2] задается исходя из априорных сведения о возможном периоде потока.
[4] rbinom(m, n, p) -возвращает вектор из m случайных чисел, имеющих биномиальное распределение с размером n и вероятностью успеха p.
[5] runif(m, a, b) - возвращает вектор из m случайных чисел, имеющих равномерное распределение на интервале [a,b].
[6] qpois(p, l)- возвращает обратное кумулятивное распределение Пуассона с l>0.
[7] rexp(m, r) - возвращает вектор из m случайных чисел, имеющих экспоненциальное распределение с коэффициентом r.
[8] mean(A, B, C, ...) - возвращает среднее значение элементов A, B, C, ...
[9] Stdev(A, B, C, ...) - возвращает среднеквадратическое отклонение для выборки элементов в A, B, C, ...
[10] pnorm(x, mu, sigma) - возвращает кумулятивное нормальное распределение вероятностей со средним mu и среднеквадратическим отклонением sigma.
[11] if(cond, x, y) - возвращает x, если истинно логическое условие cond (не равно нулю), иначе возвращает y.
[12] match(z, A) - ищет в векторе или матрице A заданное значение z и возвращает индексы его позиций в A.
[13] Коэффициент детерминации не меньше 0,995.
[14] Коэффициент детерминации не меньше 0,99
[15] Вследствие особенностей графического редактора программы Mathcad на диаграммах размер периодического потока обозначен символом N.