УДК 621.396, 621.391

АНАЛИЗ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ СТАТИСТИКИ НЕКОГЕРЕНТНОЙ МЕЖПЕРИОДНОЙ ОБРАБОТКИ

 

И. Е. Чухломин, Н. А. Файзулин

Научно-исследовательский институт по измерительной технике – радиотехнические комплексы, г. Челябинск

 

Статья получена 17 июля 2015 г., после доработки – 13 августа 2015 г.

 

Аннотация. Проведен анализ результатов последетекторной межпериодной обработки (МПО) гауссовых сигналов на фоне гауссовых помех. Исследованы параметры статистики распределения на выходе последетекторной квазиоптимальной системы МПО при заданной корреляционной матрице помехи.  

Ключевые слова: некогерентные РЛС, последетекторная межпериодная обработка.

Abstract. The analysis of results of post-detection the next periods processing of Gaussian signals is made. The research of distribution statistics parameters at the exit of post-detection system the next periods processing is carried out.

Keywords: incoherent radar, the next periods processing.

 

1. Введение

         В импульсных РЛС мм диапазона зачастую не применяется когерентная МПО пачки отраженных сигналов, это связано в первую очередь тем, что создание когерентного (опорного) гетеродина со стабильной частотой представляет технически сложную задачу [1, 2].

         В работе [2] предложена некогерентная (последетекторная) МПО на основе обеляющего фильтра в соответствии со структурной схемой (рис. 1) и указано, что выходной сигнал предпороговой статистики ξ имеет логнормальный закон распределения.

 

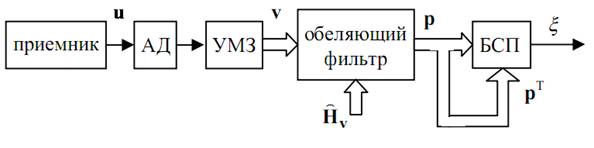
Рис. 1. Структурная схема последетекторной МПО

АД – амплитудный детектор, УМЗ – M-отводная линия задержки между зондированиями, БСП – блок скалярного перемножения, v – M-мерный вектор выходных сигналов АД, Ĥ_V – корень обратной оценочной корреляционной матрицы помех, p – M-мерный вектор выходных сигналов обеляющего фильтра, ξ – предпороговая статистика.

         Однако в статье [2] отсутствуют данные о параметрах распределения предпороговой статистики ξ  при различных размерах M – пачки зондирующих импульсов, и различных видах корреляционной матрицы (КМ) помех.

         Аналитическое определение закона распределения статистики некогерентной МПО приводит к необходимости вычисления плотности распределения случайного вектора M-элементной пачки на выходе амплитудного детектора, которая имеет вид [2]

                                                (1)

 

где

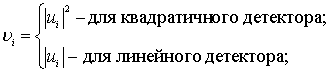
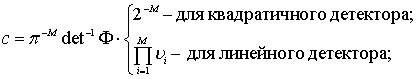
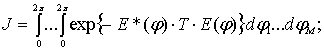                           (2)

,

 

где Ф^-1 M×M матрица, обратная КМ;

,

где L – диагональная матрица M×M с элементами = |u_i|.

            Для M ≥ 3 интеграл существенно усложняется и его выражение становится чрезмерно громоздким.

         Данная статья посвящена анализу параметров распределения статистики некогерентной МПО, при различных размерах M и различных видах заданной КМ помех. Результаты получены путем имитационного моделирования для     М = 3, 5, 8, шума, гауссовой помехи с экспоненциальной и гауссовой корреляционными функциями.

 

2. Модель МПО с заданной корреляционной матрицей помехи

         При создании модели МПО использовались следующие обозначения:

·        U_M – матрица столбец гауссова шума с мощностью

;                                                        (3)

·        Ф – ковариационная матрица помехи размера M×M

,                                         (4)

где - действительные коэффициенты корреляционной матрицы помехи при равно отстоящих отсчетах процесса;

·        H – корень матрицы Ф, треугольная матрица размера M×M

;                                                                       (5)

·        Ψ – ковариационная матрица помехи размера M×M на выходе схемы выделения модуля (линейного амплитудного детектора) [3]

;                  (6)

 

·        H ^-1 – корень матрицы Ψ^-1, треугольная матрица размера M×M

;                                                                (7)

·        Ф_I – ковариационная матрица размера M×M смеси помехи и шума

,                                                       (8)              

где η – отношение мощности гауссовой помехи к мощности шума

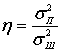,                                                                          (9)

– мощность шума, - мощность гауссовой помехи.

·        I – единичная диагональная матрица размера M×M;

·        ξ – статистика МПО

,                                                                            (10)

где

,                                

 – вектор пачки выходных сигналов после АД.

 

3. Алгоритм моделирования МПО

         Блок-схема модели оценки параметров распределения статистики МПО показана на рис. 2.

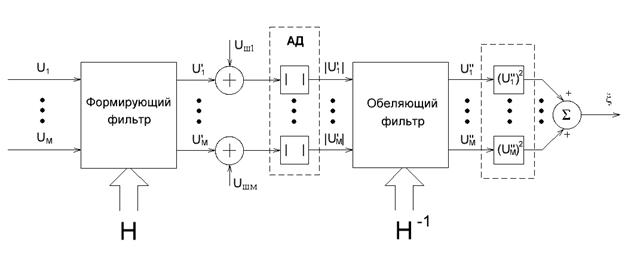
Рис. 2. Блок-схема модели оценки параметров распределения

статистики МПО

Параметры модели МПО приведены в таблице 1.

Таблица 1. Параметры модели МПО

Период дискретизации	0,15 мкс
Цена младшего разряда (ЦМР) квантователя по уровню	0,001
Конечное число выборки статистики МПО ξ	1000
Параметры входного гауссова шума UM: математическое ожидание μ=0; среднеквадратическое отклонение σ = 10.
Размер пачки зондирующих импульсов: 1.     M = 3; 2.     M = 5; 3.     M = 8.
Коэффициенты корреляции: 1.     ρ1 = 0,99; 2.     ρ1 = 0,96;
Отношение мощности гауссовой помехи к мощности шума:      η ≥ 10 дБ
Корреляционная матрица помех: 1.     Гауссова корреляционная функция (ГКФ): . 2.     Экспоненциальная корреляционная функция (ЭКФ): . 3.     Некоррелированная функция (НКФ или шум):

 

По заданным в таблице 1 коэффициентам корреляции ρ_ij и σ_п² определяется матрица Ф. Вычисление матрицы H производится в соответствии с разложением Холецкого [4].

H ∙ H ^T = Ф.                                                                         (11)

         Выходные сигналы формирующего фильтра  образуют коррелированную гауссову помеху с ковариационной матрицей Ф [7].

         Матрица Ф, образуется путем суммирования некоррелированного шума мощностью σ_ш² с выходными сигналами формирующего фильтра. Схемы выделения модуля преобразуют матрицу Ф_I  в матрицу Ψ, и вычисляется ее корень в соответствии с разложением Холецкого

.                                                                 (12)    

         Вектор выходных сигналов обеляющего фильтра равен

,                                                                   (13)

и статистика ξ равна

.                                                                  (14)

 

3. Результаты моделирования статистики распределения МПО с заданной корреляционной матрицей

         Результаты моделирования предпороговой статистики ξ достаточно точно аппроксимируются логнормальным законом распределения (Таблица 2).

Плотность распределения вероятности логнормального закона:

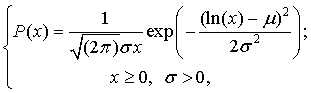                               (15)

где x – входной сигнал; σ – среднеквадратическое отклонение; μ – математическое ожидание.

Аппроксимация распределения предпороговой статистики ξ проводилась по критерию согласия Колмогорова с уровнем значимости α = 0,05 [5, 6].

 

Таблица 2. Зависимость параметров распределения статистики логнормального закона от размера пачки M.

		НКФ	ЭКФ		ГКФ
			ρ1=0,99	ρ1=0,96	ρ1=0,99	ρ1=0,96
M=3	μ	0,33	0,47	0,4	0,32	0,28
	σ	0,73	0,67	0,58	0,64	0,75
M=5	μ	0,99	0,98	1,05	0,99	1,05
	σ	0,65	0,5	0,5	0,45	0,55
M=8	μ	1,58	1,6	1,64	1,54	1,72
	σ	0,45	0,4	0,44	0,38	0,41

 

Зависимость параметров логнормального закона от пачки M изображена на рис. 4 и рис. 5.

 

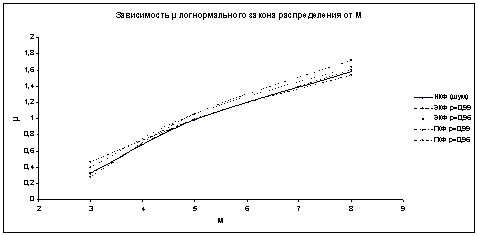
Рис. 4. Зависимость математического ожидания μ логнормального закона

распределения от размера пачки M

 

 

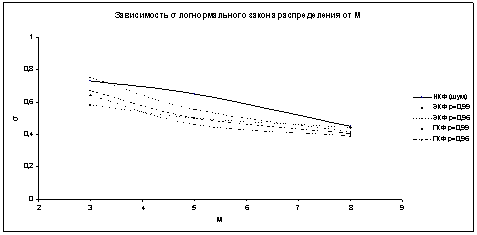
Рис. 5. Зависимость среднеквадратического отклонения σ логнормального закона распределения от размера пачки M

 

         Параметры статистики ξ при η ≥ 10 дБ практически не зависят от наличия шума, так как коэффициенты ковариационной матрицы Ф_I отличаются от соответствующих коэффициентов ковариационной матрицы Ф множителем η/(1+η), при i ≠ j и при приведении ρ_ii  к единице.

         Последующая обработка выходного сигнала МПО предполагает использование обнаружителя. Обнаружитель log-CFAR [8] использует адаптивную процедуру стабилизации ложных тревог при различных параметрах входного процесса с логнормальным распределением. 

 

4. Выводы

1. Вид закона распределения статистики некогерентной МПО на основе обеляющего фильтра не зависит от размера пачки M = 3, 5, 8 и параметров коррелированной помехи и с высокой достоверностью аппроксимируется логнормальным распределением.

2. Параметры распределения предпороговой статистики ξ зависят от размера пачки M, при этом математическое ожидание μ возрастает, а среднеквадратическое отклонение σ уменьшается практически линейно при увеличении M.

3. Постоянство вида закона распределения статистики ξ от вида КМ помех позволяет обеспечить эффективную стабилизацию ложных тревог [8].

 

Литература

1. С.И. Нефедов, М.И. Нониашвили, А.А. Лаговиер, М.Е. Голубцов. Перспективы применения миллиметровой радиолокации для обнаружения и распознавания неподвижных и движущихся объектов на фоне подстилающей поверхности. / IV Всероссийская конференция "Радиолокация и радиосвязь" – ИРЭ РАН, Москва, 2010.

2. Д.И. Леховицкий, И.Г. Кириллов, С.И. Бурковский. Особенности междупериодной обработки сигналов на фоне пассивных помех в некогерентных импульсных РЛС. // Журнал радiоелектроннi i комп'ютернi системи. – 2005. - №2 (10). – С.51-57.

URL: www.khai.edu/csp/nauchportal/Arhiv/REKS/2005/REKS205/pdf/Lehovick.pdf

3. В.И. Тихонов. Статистическая радиотехника. – 2-е изд., перераб. и доп. – М.: Радио и связь, 1982. – 624 С.

4. Численные методы условий оптимизации // под ред. Ф. Гилла и У. Мюррея. – М.: Мир, 1977. – 290 С.

5. Л.Н. Большев, Н.В. Смирнов. Таблицы математической статистики / Большев Л.Н., Смирнов Н.В. – М.: Наука. Главная редакция физико-математической литературы, 1983. – 416 С.

6. В.И. Денисов, Б.Ю. Лемешко, С.Н. Постовалов. Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим: Методические рекомендации. Часть II. Непараметрические критерии. – Москва, 2002. – 60 С.

7. Я.Д. Ширман, В.Н. Манжос. Теория и техника обработки радиолокационной информации на фоне помех. – М.: Радио и связь, 1981. – 416 С.

8. И.Е. Чухломин, Н.А. Файзулин. Анализ обнаружителя log-CFAR с цифровым адаптивным порогом обнаружения на фоне морских помех. // Журнал радиоэлектроники: электронный журнал. 2015. N2. URL: http://jre.cplire.ru/iso/feb15/7/text.pdf