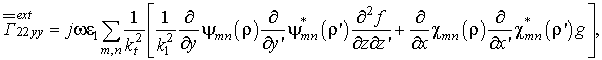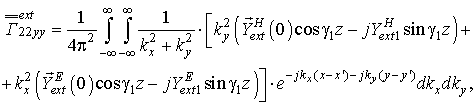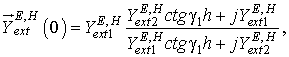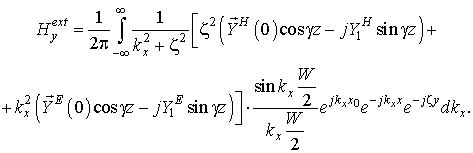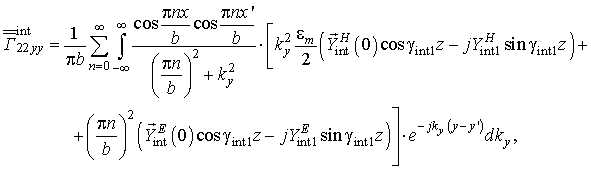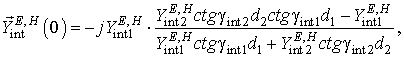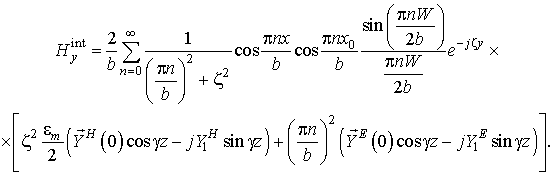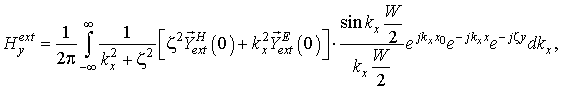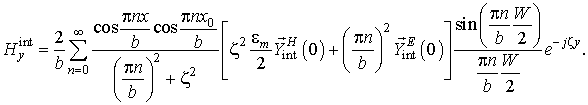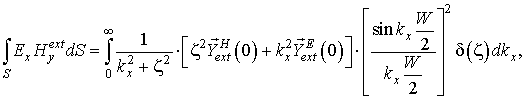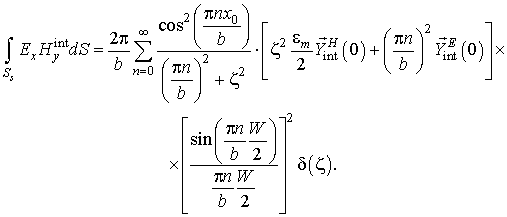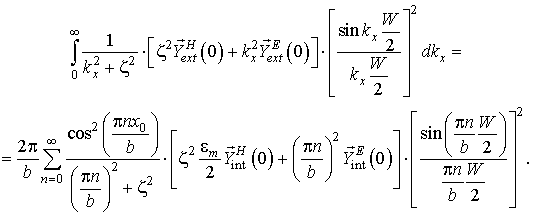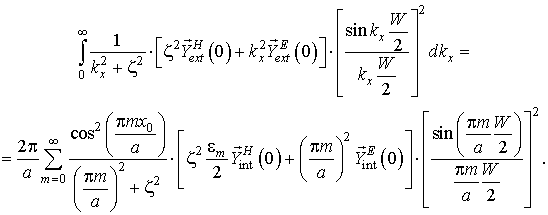АНАЛИЗ АНТЕННЫ ВЫТЕКАЮЩЕЙ ВОЛНЫ НА ОСНОВЕ ЧАСТИЧНО ЗАПОЛНЕННОГО ПРЯМОУГОЛЬНОГО ВОЛНОВОДА С ПРОДОЛЬНОЙ ЩЕЛЬЮ

 

Р. Р. Абдуллин

Уральский федеральный университет имени первого Президента России Б. Н. Ельцина

 

Статья получена 21 июля 2015 г., после доработки – 18 августа 2015 г.

 

Аннотация. Приводится методика расчета характеристик антенны вытекающих волн на основе плоских слоистых направляющих структур. В частности, в качестве основы рассматривается частично заполненный диэлектриком прямоугольный волновод с продольной щелью в узкой стенке и дополнительным защитным слоем. Представлены выражения для компонентов магнитного поля во внешнем полупространстве и пространстве внутри волновода, рассчитанные методом тензорных функций Грина стратифицированных областей. Записано дисперсионное уравнение, полученное путем сшивания полей в плоскости щели. Приведены численные результаты, представлены дисперсионные характеристики в зависимости от различных конструктивных особенностей антенны. Показана возможность расчета диаграммы направленности.

Ключевые слова: антенна вытекающей волны, прямоугольный волновод, плоская слоистая структура, тензорные функции Грина, постоянная распространения, диаграмма направленности.

Abstract: A performance calculation technique for leaky-wave antenna based on planar layered guided structures is provided. Particularly, a partially filled rectangular waveguide with long slit on narrow wall and protective cover is considered as the basis. Expressions for inside and outside magnetic field components calculated by using the Green's functions method for the stratified regions are presented. A dispersion equation obtained by fields cross linking in slit plane is written. The numeric results are provided, dispersion characteristics for different design features of antenna are presented. The possibility of radiation pattern calculation is shown.

Keywords: leaky-wave antenna, rectangular waveguide, planar layered structure, tensor Green's functions, propagation constant, radiation pattern.

 

1. Введение

Антенна вытекающей волны на основе прямоугольного волновода с продольной щелью в узкой стенке (рис.1)достаточно хорошо изучена, например в [1-3]. В указанных работах приводятся дисперсионные соотношения, полученные различными способами, например, точным методом и методом возмущения. Представлены зависимости коэффициента фазы и коэффициента затухания от размеров волновода, ширины щели, рабочей частоты. Однако, представленные решения справедливы только для основных типов волн. Также все исследования ограничиваются частным случаем однородного заполнения волновода диэлектриком, что приводит к значительным затруднениям при необходимости получения требуемых характеристик антенны. Использование частичного заполнения позволяет варьировать значение эффективной диэлектрической проницаемости и, соответственно, постоянной распространения в широком диапазоне значений. Реализуется задача сканирования диаграммы направленности в заданном диапазоне углов.

 

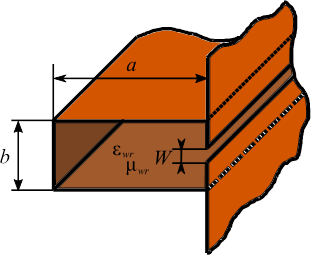
Рис. 1. Конструкция антенны вытекающей волны на основе прямоугольного волновода
с продольной щелью в узкой стенке.

 

Также не учитывается наличие защитного диэлектрического слоя, применяемого в реальных конструкциях антенн для их защиты от воздействия внешних факторов, отличающихся друг от друга в зависимости от условий эксплуатации. Защитный слой может существенно искажать полевые и частотные характеристики антенной системы в целом, и данному факту необходимо уделять внимание при проектировании.

Предлагаемый в данной статье подход не содержит описанных выше недостатков. Методика, основанная на использовании тензорных функций Грина для областей со слоистой структурой, позволяет вычислить компоненты поля в любой точке пространства от источников произвольного типа. Входящие в запись расчета компонентов поля собственные функции учитывают граничные условия распространения радиоволн в волноводе. Данные выражения позволяют строго учесть все типы колебаний, распространяющихся в рассматриваемой структуре. А характеристическая часть функции Грина, рассчитываемая методом эквивалентных линий, дает возможность оценить влияние не только внутреннего заполнения структуры диэлектриком, но и внешнего защитного слоя. Задача поиска постоянной распространения решается путем сшивания внешнего и внутреннего магнитных полей в плоскости щели. Дополнительно введена возможность поперечного смещения щели относительно ребра волновода.

Помимо разработки математического аппарата, основной задачей исследования являются получение конкретных дисперсионных зависимостей для антенны вытекающей волны в исполнении волновода с продольной щелью, оценка влияния защитного слоя, в том числе из метаматериала, и расчет диаграммы направленности исследуемой антенны.

2. Теория

Рассматриваемая антенна является модифицированной структурой, исследуемой в [1-3] (рис. 2). Она представляет собой бесконечный двуслойный прямоугольный волновод с продольной щелью в одной из узких стенок, совмещенной с проводящим экраном, покрытым слоем диэлектрика. Волновод имеет ширину a и высоту b. Центр щели смещен относительно одной из стенок на величину x₀. Ширина щели – W. Относительные диэлектрическая и магнитная проницаемости заполняющего слоя вблизи щели обозначены ε_wr1 и µ_wr1, для слоя, дальнего от щели – ε_wr2 и µ_wr2. Толщины слоев d₁ и d₂ соответственно (d₁ + d₂ = a). Защитный слой имеет толщину h, относительную диэлектрическую проницаемость  и относительную магнитную проницаемость  .

 

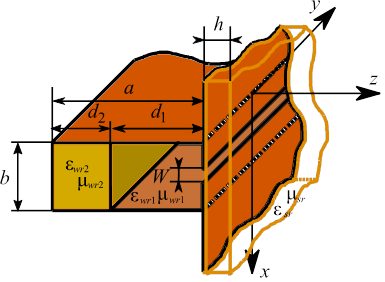
Рис. 2. Антенна вытекающей волны на основе частично заполненного прямоугольного волновода
с продольной щелью в узкой стенке и защитным слоем.

При анализе антенны сделаны следующие допущения: волновод и щель имеют бесконечную длину; толщина стенок волновода бесконечно мала; материал стенок – идеальный проводник. Координатные оси ориентированы таким образом, что граница раздела слоев диэлектрика внутри волновода соответствует координатной поверхности (рис. 2): y – вдоль оси волновода, z – перпендикулярно плоскости щели, x – перпендикулярно широкой стенке волновода.

Предполагается, что система поддерживает волну с комплексной постоянной распространения, где  – фазовая постоянная,  – постоянная затухания. Тогда комплексная постоянная распространения определяется по аналогии с [4] методом сшивания внешнего и внутреннего магнитных полей в плоскости щели. В этом случае элемент связи, то есть щель в стенке волновода, рассматривается в качестве источника возбуждения электромагнитных полей, распространяющихся как вне направляющей структуры, так и внутри нее. При прохождении электромагнитной волны через элемент связи из закрытой области внутри волновода во внешнее открытое полупространство, в плоскости щели выполняется условие непрерывности компонент электрического и магнитного полей. Тогда сумма плотностей потоков энергии, излучаемых щелью в противоположных направлениях, должна равняться нулю:

                                                 (1) 

                               

где  – компонента электрического поля в щели;  и  – компоненты магнитного поля вблизи щели со стороны внешнего полупространства и прямоугольного волновода соответственно; штрихи означают точки источника магнитного поля.

В свою очередь магнитные поля закрытой области  и свободного полупространства из (1) определяются магнитным током в щели   и функцией Грина соответствующих областей:

                                             (2)

 

В выбранной системе координат функция Грина в общем виде при разложении по волнам типов E и H записывается следующим образом [5]:

            (3)

 

где – собственные числа;  и – абсолютная диэлектрическая проницаемость и постоянная распространения в примыкающем к щели слое. Функции  и  являются ортонормированными собственными функциями двумерных скалярных уравнений ,  с граничными условиями  на проводящей поверхности или условиями расходимости волн в случае открытых областей;   и – характеристические части функции Грина, описывающие взаимодействие полей между слоями диэлектрика [5]. Они учитывают условия непрерывности на границах раздела диэлектриков.

В случае открытых областей знак суммы в (3) заменяется на интеграл по волновым числам. Тогда собственные числа , где  и  – постоянные распространения вдоль осей x и y, соответственно. А собственные функции  [6]. При раскрытии характеристической части функция Грина для свободного полупространствапринимает вид:

                                       (4) 

где  –продольная постоянная распространения в защитном слое диэлектрика (под продольными здесь понимаются волновые числа вдоль оси z); – постоянная распространения в защитном слое;  – волновое число в свободном пространстве; , – эквивалентные волновые проводимости защитного слоя в плоскости H и плоскости E соответственно; , ;; и – входные проводимости свободного полупространства в плоскости H и E с учетом наличия защитного слоя, пересчитываемые по рекуррентным формулам к сечению в плоскости щели [7]:

                                                                     (5)      

                      

где , , .

 

После подстановки (5) в (2) внешнее магнитное поле определяется как:

                                                (6)            

Поле внутри волновода определяется аналогичным образом. Внутренняя область ограничена по оси x и не ограничена по оси y. В этом случае собственные числа принимают вид , а собственные функции – и [6], где n – число полуволн, укладывающихся вдоль узкой стенки волновода; – символ Кронекера, принимающий значение если n = 0, и  если n ≠ 0. Следовательно, выражение для функции Грина во внутренней области:

                        (7)

где  – постоянная распространения внутри волновода в слое, примыкающем к щели; , , , . Входные проводимости в плоскости щели рассчитываются по формуле:

                                                            (8)                   

 

где , , , , .

 

После подстановки (7) в (2) магнитное поле внутри волновода:

                              (9)   

Компоненты внешнего и внутреннего магнитного полей должны иметь одинаковые значения в плоскости щели z = 0. Данный факт лежит в основе метода сшивания полей. Таким образом, (6) и (9) принимают вид:

                          (10) 

                   (11)

Тогда в плоскости щели должны быть равны друг другу и мощности, излучаемые наружу и внутрь волновода, определяемые путем умножения (10) и (11) слева на электрическую компоненту:

                                (12)    

                                    (13)

Переход к мощностям позволяет свести к минимуму количество переменных в итоговом уравнении. За счет интегрирования по поверхности щели, необходимого для расчета мощностей, излучаемых как во внешнюю, так и внутреннюю области, удается избавиться от привязки к реальным координатам и перейти к пространству волновых чисел. 

Таким образом, трансцендентное уравнение для поиска неизвестной постоянной распространения получается путем приравнивания друг другу правых частей (12) и (13):

                           (14)    

Уравнение (14) является универсальным и может быть применимо даже в особом случае открытого волновода (W = b), описанного в [2]. Данная ситуация имеет несколько отличий в сравнении со случаем узкой щели. Основное из них заключается в отсутствии проводящего экрана на границе раздела областей. Однако благодаря выбранной ориентации системы координат собственные функции сохраняют свой вид, и применение (14) остается справедливым.

При помощи данной методики также может быть рассчитана постоянная распространения для антенны вытекающей волны на основе прямоугольного волновода с продольной щелью в широкой стенке. В этом случае в (14) необходимо осуществить взаимные замены , а n заменить на m – число полуволн, укладывающихся вдоль широкой стенки:

                         (15)

Как известно при работе прямоугольного волновода на основной волне H₁₀, продольная щель, расположенная посередине широкой стенки, является неизлучающей [8]. Это легко показать при подстановке  и m = 1 в (15). Правая часть (15) обращается в нуль, и оно не имеет решения при любых ζ.

Несмотря на все достоинства разработанного метода следует обратить внимание на одно ограничение: использование значения ширины щели W = 0 в   некорректно, так как возникает особый случай закрытого волновода, и тогда внешнее и внутренне магнитные поля не связаны между собой посредством щели.  

3. Численные результаты

Трансцендентное уравнение (14) имеет сложную форму и не решается аналитически, поскольку описывает все гармоники внутри волновода и все типы слоистых структур. Однако на следующем шаге получения численных результатов изначальные выражения могут быть существенно упрощены для каждого частного случая. В первую очередь это относится к расчету входных проводимостей. Например, как следует из (5), для случая антенны без защитного слоя (h = 0) входная проводимость внешней области . Другими словами, она определяется только параметрами окружающей среды. Также для случая полого волновода (d₂ = 0, d₁ = a) входная проводимость области внутри волновода в плоскости щели, рассчитываемая в соответствии с (8), определяется только эквивалентной проводимостью вакуума: .

Для получения численных результатов использована модель волновода со стандартным внутренним сечением 23×10 мм. Рассмотрены случаи полого волновода, частично заполненного волновода, полого волновода с защитным слоем, частично заполненного волновода с защитным слоем.

Предложенная методика позволяет проводить анализ структур, имеющих в своем составе композитный материал с отрицательным коэффициентом рефракции (так называемый метаматериал), применение которого в качестве диэлектрика защитного слоя позволит добиться практически стопроцентной эффективности излучения антенны в некотором диапазоне частот [9]. На первоначальном этапе оценки влияния метаматериала на характеристики антенны сделано упрощение, заключающееся в том, что значения отрицательных проницаемостей защитного слоя заданы константой во всем рассматриваемом диапазоне частот без привязки к конкретному исполнению ячейки композита.

На рис. 3 приведены зависимости коэффициента замедления антенны без защитного слоя от величины смещения центра щели относительно широкой стенки волновода, заполненного вакуумом, где – волновое число в свободном пространстве. Рабочая частота ­– 9 ГГц. Ширина щели W варьируется от 1 до 8 мм.

Наличие щели в узкой стенке приводит к искажению картины электромагнитного поля внутри структуры по сравнению со случаем закрытого волновода. С увеличением ширины щели происходит увеличение излучаемой наружу мощности и снижение фазовой скорости волны, распространяющейся в структуре. В рассматриваемом случае система работает на основной волне H₁₀, и потому максимальное замедление происходит при размещении щели посередине узкой стенки. 

На рис. 4 приведены графики зависимости коэффициента замедления исследуемой антенны без защитного слоя от степени заполнения волновода диэлектриком. Параметры заполнения выбраны следующим образом: относительная диэлектрическая проницаемость ε_wr = 2; относительная магнитная проницаемость µ_wr = 1. Щель расположена строго на середине узкой стенки. Ширина щели W = 1 мм.

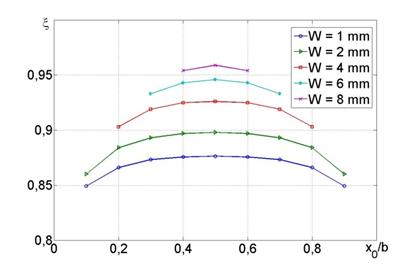
Рис. 3. Зависимость коэффициента замедления основной волны полого волновода
с продольной щелью без защитного слоя от положения щели.

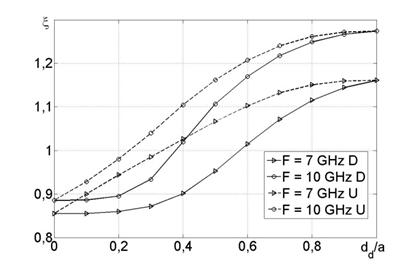
Рис. 4. Зависимость коэффициента замедления антенны без защитного слоя от степени заполнения волновода диэлектриком:
сплошные линии – диэлектрик расположен у дальней от щели стенки (D); штриховые линии – диэлектрик у стенки со щелью (U).

Наличие диэлектрика в волноводе оказывает существенное влияние на характеристики антенны, увеличивающееся с ростом рабочей частоты. С увеличением толщины диэлектрического слоя внутри волновода фазовая скорость в структуре уменьшается. А изменение рабочей частоты приводит к изменению крутизны зависимости коэффициента замедления от степени  заполнения волновода диэлектриком в соответствующую сторону. Таким образом, для достижения аналогичных характеристик системы при ее работе на более высокой частоте возможно применение слоя диэлектрика меньшей толщины. Причем наибольшее влияние на значение коэффициента замедления имеет материал, расположенный в непосредственной близости со щелью.

На рис. 5 представлены частотные зависимости коэффициента замедления  для полого волновода при различных значениях относительной диэлектрической проницаемости защитного слоя ε_sr. Щель расположена посередине узкой стенки и имеет ширину W = 1 мм. Толщина защитного слоя выбрана h = 0,5 мм, относительная магнитная проницаемость µ_sr= 1.

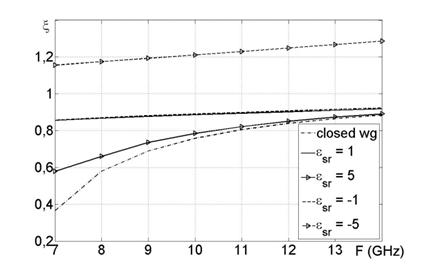
Рис. 5. Коэффициент замедления прямоугольного волновода с защитным слоем

 

Защитный слой имеет большое влияние на характеристики антенны. Его наличие в большей степени сказывается при работе системы на более низких частотах. Увеличение рабочей частоты приводит к увеличению коэффициента замедления вне зависимости от знака и модуля диэлектрической проницаемости защитного слоя. С ростом модуля при разных знаках наблюдается противоположный эффект. При увеличении положительной проницаемости наблюдается рост фазовой скорости, и вид дисперсионной характеристики структуры стремится к характеристике закрытого волновода. При увеличении отрицательной проницаемости происходит снижение фазовой скорости, а также критической частоты рассматриваемой системы.

На рис. 6 приведена двумерная зависимость коэффициента замедления от величин относительных диэлектрической и магнитной проницаемостей защитного слоя. Толщина слоя выбрана h = 0,5 мм. Рабочая частота F = 9 ГГц.

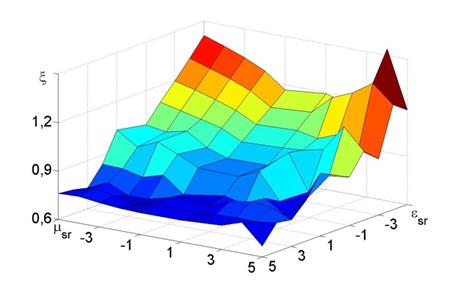
Рис.6. Двумерная зависимость коэффициента замедления от проницаемостей защитного слоя.

 

Наилучшим образом зависимость выражена в области, где материал защитного слоя обладает отрицательным коэффициентом рефракции. Здесь значение коэффициента замедления увеличивается с ростом модуля проницаемостей. В остальных областях дисперсионная поверхность не имеет столь очевидных тенденций и требует дальнейших исследований.

На рис. 7 показана двумерная зависимость коэффициента замедления ξ прямоугольного волновода с продольной щелью в узкой стенке от степени заполнения волновода диэлектриком и толщины защитного слоя. Использованы следующие параметры: относительная диэлектрическая проницаемость защитного слоя ε_sr = 2 и относительная магнитная проницаемость µ_sr = 1. Диэлектрик внутри волновода имеет относительные диэлектрическую и магнитную проницаемости ε_wr = 2 и µ_wr = 1, соответственно. Ширина щели выбрана W = 1 мм. Результаты представлены для рабочей частоты F = 9 ГГц. Диэлектрический слой расположен у дальней от щели стенки.

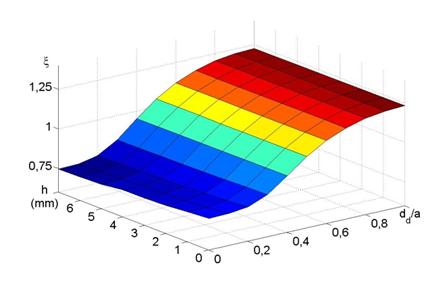
Рис. 7. Двумерная зависимость коэффициента замедления от степени заполнения волновода диэлектриком и толщины защитного слоя.

 

4. Диаграмма направленности

Для расчета диаграммы направленности (ДН) антенны вытекающей волны на основе частично заполненного прямоугольного волновода с продольной щелью и защитным диэлектрическим слоем необходимо определить компоненты поля в каждой точке дальней зоны. Например, составляющая поля вдоль оси волновода может быть рассчитана в соответствии с (6) при подстановке уже известного значения постоянной распространения ζ. Для расчета составляющих вдоль осей x и z необходимо использовать функции  и , соответственно.

При упрощенном анализе исследуемая антенна может быть представлена в качестве идеального линейного излучателя конечной длины. Тогда на основе зависимостей, представленных на рис. 3–7, может быть рассчитана форма ее диаграммы направленности, а также оптимальная длина структуры из условия Хансена–Вудворда [10]. Например, диаграмма направленности в плоскости H антенны вытекающей волны длиной l:

                                                                                                     (16)                                       

где , – физический угол наблюдения, отсчитываемый от продольной оси волновода y.

Положение главного максимума рассчитывается из условия . Отсюда следует, что , при . То есть увеличение коэффициента замедления приводит к наклону максимума диаграммы направленности в сторону, противоположную от источника возбуждения, пока антенна не сменит режим излучения на осевой (рис. 8). Дальнейший рост коэффициента замедления () приводит к одновременному сужению основного лепестка ДН и росту боковых лепестков, то есть к снижению направленности, полностью исчезающей при  [10].

Ранее было показано, что применение частичного диэлектрического заполнения и дополнительного защитного слоя позволяет варьировать постоянную распространения в широком диапазоне значений. Соответственно, может быть осуществлено сканирование диаграммы направленности в широком диапазоне углов. И даже величина поперечного смещения продольной щели относительно стенки волновода вносит существенный вклад при формировании ДН в плоскости оси антенны.

Следует отметить, что здесь не идет речи о динамическом изменении параметров антенны. Имеется ввиду следующее: путем сочетания параметров диэлектрического заполнения волновода и защитного слоя (толщины, положения, проницаемостей) можно добиться оптимальной формы дисперсионной кривой, которая обеспечит сканирование диаграммы направленности в заданном диапазоне углов при заданной девиации частоты.

 

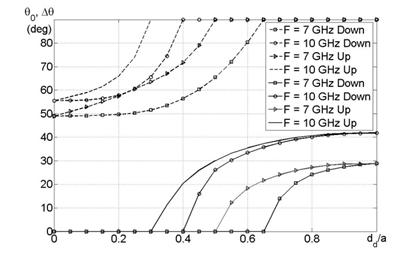
Рис. 8. Характеристики излучения антенны вытекающей волны без защитного слоя: штриховые линии – наклон ДН; сплошные линии – ширина ДН по нулям излучения для антенны оптимальной длины в осевом направлении.

5. Заключение

Метод тензорных функций Грина является наиболее универсальным способом решения задач электромагнитного возбуждения, отличающимся прозрачностью алгоритма использования и позволяющим анализировать плоские слоистые структуры, в том числе имеющие в своем составе материалы с отрицательными значениями диэлектрической и магнитной проницаемостей.

Сочетание параметров диэлектрического заполнения и защитного слоя в конструкции антенны вытекающей волны позволяет скорректировать форму дисперсионной кривой, обеспечивая стабильность полевых характеристик в заданном диапазоне частот либо сканирование диаграммы направленности в заданном диапазоне углов.

Предложенная методика проектирования антенны вытекающей волны на основе частично заполненного прямоугольного волновода с продольной щелью и защитным слое основана на использовании матричных методов и позволяет получать компактные программы в среде MatLab, существенно превосходящие по точности и быстродействию специализированное ПО, например HFSS.

 

Исследование выполнено за счет гранта Российского научного фонда (проект №14-19-01396). 

 

Литература

1.     C.H. Walter. Traveling wave antennas, McGraw-Hill, 1965, Dover, 1970, reprinted by Peninsula Publishing, Los Altos, California, 1990.

2.     L.O. Goldstone, A.A. Oliner. Leaky-wave antenna I: rectangular waveguides. IRE Transactions on Antennas and  propagation. pp. 307-319. October, 1959.

3.     A.A. Oliner, D.R. Jackson, “Leaky-wave antennas” in AntennaEngineering Handbook, J. L. Volakis, Ed., chapter 11, McGraw-Hill,New York, NY, USA, 4th edition, 2007.

4.     R.R. Abdullin, Yu.E. Mitelman, S.N. Shabunin. “Radiation pattern of leaky-wave antenna based on partially-filled rectangular waveguide”. Loughborough Antenna & Propagation Conference 2014, 10-11 November, 2014. Loughborough, UK.

5.     Панченко Б.А.  "Функция Грина уравнений Максвелла для областей частично заполненых диэлектриком".// Проблемы повышения эффективности и качества радиотехнических систем. Межвузовский сборник. Вып. 2. Свердловск, изд. УПИ им. С. М. Кирова, 1979. с. 29–36.

6.     Фелсен Л., Маркувиц Н. Излучение и рассеяние волн. Том 1. М.: Мир. 1978. 555 с.

7.     Панченко Б.А., Нефедов Е.И. Микрополосковые антенны. М.: Радиоисвязь. 1986.  144 с.

8.     Гольдштейн, Л. Д. Электромагнитные поля и волны / Л. Д. Гольдштейн, Н. В. Зернов. − М. : Советское радио, 1972.

9.     Shabunin S.N. Excitations of space and surface waves by patch and slot antennas on metamaterial grounded slab // European Conference on Antennas and Propagation: EuCAP 2006. 6 –10 November 2006.  Nice, France. CD//PA6//347175.pdf.

10. Сазонов Д.М. Антенны и устройства СВЧ. М.: Высш. шк. 1988. 432 с.