|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 12, 2002 |
|
ОПТИМИЗАЦИЯ ПОИСКА УСЛОВНО ДЕТЕРМИНИРОВАННОЙ ДИНАМИЧЕСКОЙ ЦЕЛИ БОЛЬШОЙ ПОИСКОВОЙ СИСТЕМОЙ
А. А. Строцев
Ростовский военный институт ракетных войск
Получена 18.12.2002 г.
В статье рассмотрен синтез равномерно оптимального управления поиском в большой поисковой системе, в случае, когда движение цели можно считать условно детерминированным.
Введение. В [1] рассмотрена задача поиска неподвижной цели многопозиционной информационной системой. Однако искомая цель часто является подвижной с детерминированными уравнениями динамики и стохастическими начальными условиями. Поиск таких целей с условно детерминированным движением рассмотрен, например, в [2]. В отличие от задач поиска неподвижной цели оптимизация поиска условно детерминированных динамических целей не позволяет в общем случае получить равномерно оптимальные стратегии поиска. Т.е. стратегии, обладающей свойством: поиск, который заканчивается в произвольный момент времени, оптимален. Отметим, что в практическом плане применение именно равномерно оптимальных стратегий поиска приводит к реализации оптимального поиска в быстро меняющейся обстановке практически в каждый момент времени. Таким образом, синтез равномерно оптимального управления поиском целей с условно детерминированным движением является актуальной задачей.
1.Постановка
задачи. Рассматривается большая
поисковая система, действия отдельных поисковых единиц которой описываются
функцией плотности поиска (стратегией поиска) ![]() ,
, ![]() [2].
Положение новой цели в области поиска
[2].
Положение новой цели в области поиска ![]() задаётся начальной плотностью
распределения
задаётся начальной плотностью
распределения ![]() . Уравнение движения цели имеет вид:
. Уравнение движения цели имеет вид:
ż=f(z,v,t) (1)
где ![]() ,
, ![]() - вектор управления,
- вектор управления, ![]() ,
, ![]() .
.
Тогда уравнение динамики апостериорной плотности распределения положения цели может быть получено в виде [2]
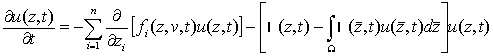 ,
(2)
,
(2)
![]() ,
(3)
,
(3)
где
![]() обладает
следующими свойствами:
обладает
следующими свойствами:
1.
![]() ;
; ![]() для всех
для всех ![]() ,
,![]() ; (4)
; (4)
2.
![]() - есть вероятность обнаружения
цели в интервале времени
- есть вероятность обнаружения
цели в интервале времени ![]() при условии, что цель находится в
некоторой небольшой области
при условии, что цель находится в
некоторой небольшой области ![]() точки
точки ![]() и не обнаружена до момента
и не обнаружена до момента ![]() .
.
Полагается,
что область поиска ![]() , динамика цели, описываемая выражением
(1), и начальная плотность распределения положения цели
, динамика цели, описываемая выражением
(1), и начальная плотность распределения положения цели ![]() таковы,
что
таковы,
что 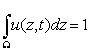 для
всех
для
всех ![]() .
.
Требуется найти равномерно оптимальную по критерию
минимума вероятности необнаружения цели к моменту времени ![]() стратегию поиска для
задачи (2)-(4).
стратегию поиска для
задачи (2)-(4).
2. Модель задачи синтеза равномерно оптимальной стратегии поиска условно детерминированной цели. Преобразуем исходную задачу. Уравнение (2) сводится к линейному с использованием подстановки
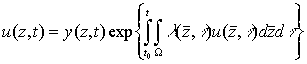 , (5)
, (5)
где
ненормированная мера ![]() определяется как вероятность того, что
цель находится в некоторой небольшой области
определяется как вероятность того, что
цель находится в некоторой небольшой области ![]() точки
точки ![]() и не обнаружена до
момента
и не обнаружена до
момента ![]() .
.
Подставляя (5) в (2) и (3) получим
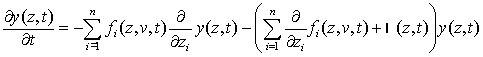 ,(6)
,(6)
![]() .
(7)
.
(7)
Обозначим
![]() ,
(8)
,
(8)
![]() ,
, ![]() . (9)
. (9)
Тогда характеристические уравнения для (6), (7) принимают вид:
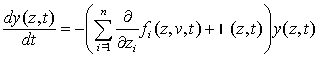 ,
, ![]() ,
(10)
,
(10)
![]() ,
, ![]() , (11)
, (11)
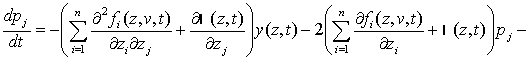
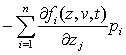 ,
, ![]() , (12)
, (12)
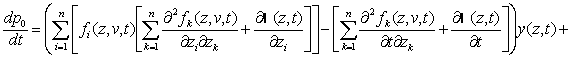
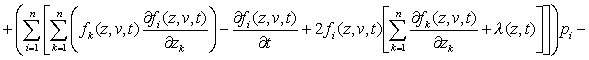
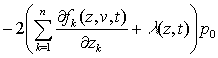 ,
(13)
,
(13)
При этом требуется найти ![]() минимизирующую вероятность необнаружения
цели к моменту времени
минимизирующую вероятность необнаружения
цели к моменту времени ![]() [2]:
[2]:
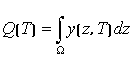 . (14)
. (14)
Разложим функцию ![]() в
ряд Тейлора в окрестности опорной траектории
в
ряд Тейлора в окрестности опорной траектории ![]() ,
заданной уравнением
,
заданной уравнением
![]() ,
, ![]() . (15)
. (15)
Полагая отклонения от опорной траектории малыми и ограничиваясь линейными членами ряда, выражение (1) с учётом (15) перепишем в виде
![]() , (16)
, (16)
где
![]() ,
,
![]() .
.
Подставляя (16) в (10) получим независимое от других переменных системы (10)-(13) уравнение
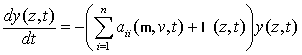 ,
, ![]() . (17)
. (17)
Для каждого ![]() решение (17) можно записать в виде
решение (17) можно записать в виде
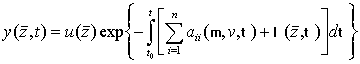 . (18)
. (18)
Таким образом, получаем следующую задачу нахождения
оптимальной стратегии поиска ![]() :
:
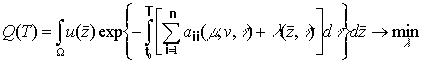 , (19)
, (19)
![]() ;
; ![]() для всех
для всех ![]() ,
, ![]() .
(20)
.
(20)
Отметим, что ![]() связано с решением исходной задачи через
решение (16):
связано с решением исходной задачи через
решение (16):
![]() , (21)
, (21)
где ![]() - фундаментальная матрица системы (16),
- фундаментальная матрица системы (16), ![]() ,
,
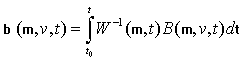 . (22)
. (22)
Т.е., учитывая (21), (22),
![]() .
(23)
.
(23)
Полученная модель исходной задачи отличается от случая неподвижной цели наличием в функционале известных элементов уравнения динамики цели, которые не влияют на свойства получаемого решения. Т.е. для задачи (19), (20) можно применить разработанный, например, в [2], [3] для неподвижной цели аппарат и получить равномерно оптимальную стратегию поиска. Однако часто достаточно получить приближённое численное решение задачи.
3. Алгоритм приближённого решения оптимизационной
задачи. Поскольку рассматриваемое в
такой постановке задачи управление поиском ![]() не будет в точности
воспроизводиться некоторой реальной системой [2], то достаточно найти
приближённое решение.
не будет в точности
воспроизводиться некоторой реальной системой [2], то достаточно найти
приближённое решение.
Перейдём к дискретному приближению исходной задачи.
Разобьем интервал ![]() на
на ![]() частей длительностью
частей длительностью ![]() точками
точками
![]() . Положим, что интеграл
. Положим, что интеграл 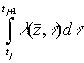 практически постоянен на достаточно малых областях
практически постоянен на достаточно малых областях ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и представим
в виде
и представим
в виде
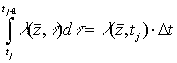 . (24)
. (24)
Тогда (19) представимо
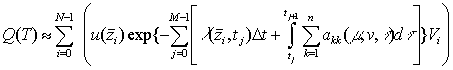 , (25)
, (25)
где
![]() ,
, ![]() , а ограничение (20)
, а ограничение (20)
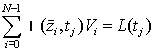 . (26)
. (26)
Введём обозначения
![]() ,
,
![]() ,
,
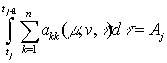
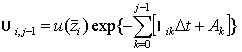 ,
(27)
,
(27)
тогда решение задачи (19), (20) сводится к последовательному решению следующих задач математического программирования:
найти
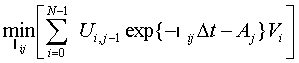 , (28)
, (28)
в условиях ограничений
![]() ,
, 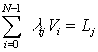 ,
, ![]() ,
, ![]() . (29)
. (29)
Переход от оптимального решения (28), (29) ![]() к
оптимальному решению исходной задачи
к
оптимальному решению исходной задачи ![]() осуществляется в соответствии с (23):
осуществляется в соответствии с (23):
![]() . (30)
. (30)
Отметим, что (27), (28) отражают свойство равномерно оптимальной стратегии поиска, отмеченной Аркиным в [3].
4.
Пример синтеза равномерно
оптимальной стратегии поиска условно детерминированной динамической цели. В качестве примера применения построенного в п.3 алгоритма
рассмотрим синтез равномерно оптимальной стратегии поиска в следующей задаче: ![]() ,
, ![]() - отрезок
- отрезок ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() .
.
Начальная плотность
распределения положения цели задана в виде нормальной плотности распределения ![]() .
.
Требуется
найти ![]() ,
,
![]() ,
, ![]() .
.
В результате решения последовательности задач математического программирования вида (28), (29), с учётом (30) получим оптимальную стратегию поиска, вид которой показан на рис. 1.
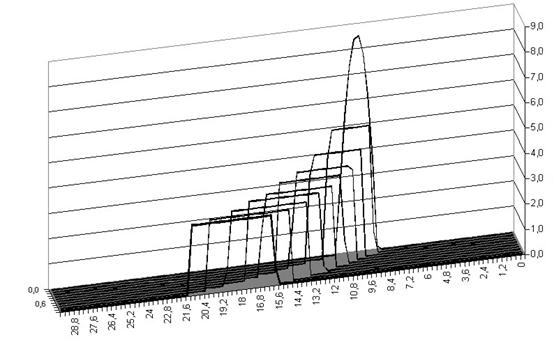
Рис.1
Из
анализа рис.1 видно, что полученная стратегия поиска обладает свойством,
отмеченным в [2], [3] применительно к равномерно оптимальной стратегии поиска
неподвижной цели: существует область ![]() , увеличивающаяся со временем, такая, что
стратегия поиска положительна внутри области
, увеличивающаяся со временем, такая, что
стратегия поиска положительна внутри области ![]() и равна нулю в
и равна нулю в ![]() .
.
При
применении ![]() значение
вероятности необнаружения цели в условиях рассматриваемого примера равна
значение
вероятности необнаружения цели в условиях рассматриваемого примера равна ![]() , а
при равномерном распределении поисковых усилий
, а
при равномерном распределении поисковых усилий ![]() ,
что более чем на порядок больше.
,
что более чем на порядок больше.
Заключение. Синтез равномерно оптимальных стратегий в задаче оптимального поиска условно детерминированной динамической цели достигнут за счёт использования независимости части характеристических уравнений при некотором упрощении модели движения цели. Однако в отличие от задач наблюдения в задаче поиска это упрощение не оказывает значительного влияния.
СПИСОК ЛИТЕРАТУРЫ
1. Строцев А.А. Оптимальный поиск неподвижной цели многопозиционной информационной системой. – Интернет-публикация, М.: Журнал радиоэлектроники , № 4, 2002.
2. Хеллман О. Введение в теорию оптимального поиска. – М.: Наука, 1985.
3. Аркин В.И. Задачи оптимального распределения поисковых усилий. – Теория вероятностей и её применения, 1964, т. 9, № 1.
|
|
|