|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 12, 2003 |
|
МАТЕМАТИЧЕСКОЕ ПРОЕКТИРОВАНИЕ ТРЕХМЕРНЫХ ВОЛНОВОДНЫХ ПЕРЕХОДОВ
А. Н. Боголюбов, И. А. Буткарев
Московский Государственный Университет им. М. В. Ломоносова, Физический факультет
Рассмотрены две электродинамические задачи расчета волноводных переходов. На основе метода регуляризации А.Н. Тихонова и метода скользящего допуска предложен общий алгоритм решения задач синтеза таких переходов. Приведен пример решения конкретной задачи. Проведено исследование эффективности распараллеливания метода скользящего допуска в случае применения компьютерных кластеров.
1. ВВЕДЕНИЕ
Задачи математического проектирования волноведущих электродинамических систем являются типичными обратными задачами и для их решения наиболее эффективными оказываются методы регуляризации А.Н. Тихонова [1,2]. В статье рассматривается специфика реализации этих методов для двух классов задач. В первом случае рассматривается переход между двумя регулярными металлодиэлектрическими волноводами, граница которых звездная и достаточно гладкая, при этом заполнение перехода предполагается неоднородным и изотропным. Во втором случае рассматривается переход между прямоугольным и компланарным волноводами с однородным заполнением. Предполагается, что граница волноводов и перехода является идеально проводящей.
2. Переход между двумя металлодиэлектрическими волноводами
Рассмотрим задачу синтеза согласующего волноводного перехода [3], соединяющего два металло-диэлектрических волновода рис. 1. Будем предполагать, что граница волноводов и волноводного перехода достаточно гладкая и идеально проводящая. Волноводы считаем регулярными, т.е. их заполнение и геометрия поперечного сечения зависят только от поперечных координат. Заполнение перехода может зависеть как от поперечных, так и от продольных координат. Такая постановка является достаточно общей и позволяет рассматривать задачу синтеза весьма широкого класса волноводных переходов, применяющихся в сверхвысокочастотной электродинамике, волоконной и интегральной оптике.
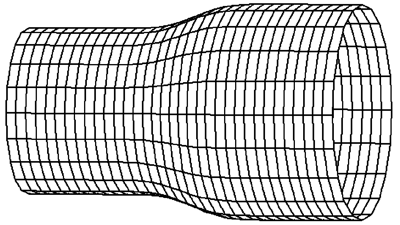
Рис. 1. Переход между двумя металлодиэлектрическими волноводами.
Введем цилиндрическую систему координат, ось которой совпадает с осью рассматриваемой волноведущей системы, а начало – с входным сечением волноводного перехода. Левый волновод будем называть входным, а правый – выходным. Пусть граница поперечного сечения входного волновода описывается функцией h(j,0), а диэлектрическое заполнение – функцией e(r,j,0). Граница поперечного сечения и диэлектрическое заполнение выходного волновода описывается соответственно функциями h(j,L) и e(r,j,L), где L – длина волноводного перехода, которая считается заданной. Граница поперечного сечения перехода описывается функцией h(j,z), а диэлектрическое заполнение – функцией e(r,j,z). В дальнейшем будем предполагать, что функции h и e обладают производными до второго порядка включительно.
Рассматривая стационарную постановку задачи с временной зависимостью exp(-iwt) и исключая из системы уравнений Максвелла в отсутствие токов и свободных зарядов продольные компоненты (Ez,Hz) электромагнитного поля, получим систему из четырех уравнений в частных производных второго порядка относительно поперечных компонент Y={Ex,Ey,Hx,Hy}T поля.
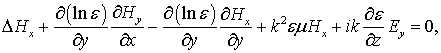 |
(1) |
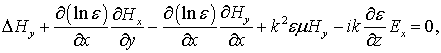 |
(2) |
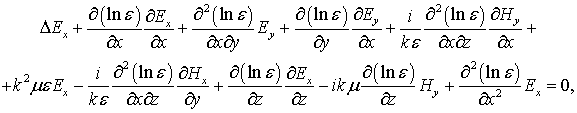 |
(3) |
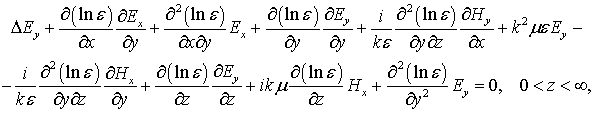 |
(4) |
| (5) | |
| (6) |
Здесь вектор-столбец Y0 задает распределение поля на выходе левого волновода, Pi – матрицы, зависящие от e, m и волнового числа k=w/c, S – боковая поверхность, Et – тангенциальная составляющая вектора напряженности электрического поля. Вместе с граничными условиями (5), начальными условиями (6) и условиями при z®¥ система (1)-(4)образует начально-краевую задачу, моделирующую процесс распространения электромагнитных волн в таком переходе.
Сделаем замену переменных в системе (1)-(4), которая позволит привести границу перехода к цилиндрической форме:
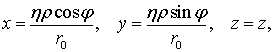 |
(7) |
где r=rr0/h(j,z), а r0 – радиус полученного прямого кругового цилиндра. Легко убедиться, что преобразование переменных (7) является невырожденным.
Для того чтобы получить устойчивый конечно-разностный алгоритм решения прямой задачи расчета волноводного перехода, воспользуемся методом параболического приближения [4]. В результате получим постановку задачи в параболическом приближении, которую можно записать в матричном виде:
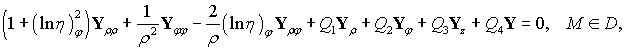 |
(8) |
| (9) | |
| (10) |
где Qi (i=1¸4) – матрицы размерности 4´4.
Для решения задачи (8)-(10) построена разностная схема с весами. Полученная разностная начально-краевая задача представляет собой систему из 4M(N+1) линейных алгебраических уравнений, матрица которой имеет блочно-ленточную структуру. Здесь N+1 и M – количество узлов сетки вдоль радиальной и угловой координаты соответственно. Данная система решается с помощью метода исключения Гаусса, модифицированного с учётом структуры матрицы. Каждое решение системы позволяет сделать шаг hz=L/Nz вдоль оси z. Решив Nz таких систем, получим распределение поля на выходе волноводного перехода. Таким образом, получается весьма экономичный и достаточно универсальный алгоритм, позволяющий многократно решать прямую задачу расчета волноводного перехода в процессе его синтеза.
Задачу синтеза рассмотрим как задачу построения такого перехода, который обеспечивает максимальную амплитуду поля Hx в выходном сечении при заданном поле на входе. Для этого используем метод регуляризации А.Н. Тихонова. Строим сглаживающий функционал:
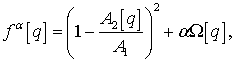 |
(11) |
где q – набор параметров оптимизации; A1 – амплитуда поля во входном сечении; A2[q] – амплитуда поля в выходном сечении; a – параметр регуляризации; W[q] – стабилизатор. В соответствии с методом регуляризации решением задачи синтеза считаем такой набор параметров оптимизации, который доставляет минимум сглаживающему функционалу:
| (12) |
где с помощью множества Q накладываются ограничения на параметры перехода.
Рассмотрим конкретную задачу синтеза перехода между двумя круглыми волноводами радиусов r1 и r2, имеющими однородные различные заполнения e1 и e2. Фиксируем длину перехода L. Построим переход, который имеет круглые сечения и однородное по сечению заполнение. Ищем профиль перехода в форме кубического сплайна, состоящего из трех частей:
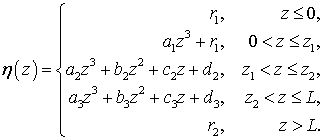 |
(13) |
Коэффициенты ai, bi, ci, di в этой формуле подбираются из условия гладкости второго порядка. Аналогичным образом строится функция диэлектрической проницаемости. В результате получаем четыре параметра оптимизации q={z1,z2,z3,z4}. На параметры оптимизации накладываются естественные ограничения:
Для поиска оптимального набора параметров применяется метод скользящего допуска, основанный на методе Нелдера и Мида [5].
Рассмотрим согласующий переход между круглыми волноводами со следующими параметрами:
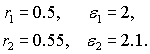 |
Пусть через входной волновод распространяется мода ТМ00 с k=1000, h=1414.2. Пусть L=2. В качестве первого приближения при оптимизации используются следующие параметры: q0={0.7,1.4,0.6,1.3}. Для решения данной конкретной задачи была выбрана сетка с N=15, M=24, Nz=100. Стабилизатор был выбран в виде: W[q]=||q-0.5LI||2, где I – вектор состоящий из единиц.
На рис. 2 и 3 представлены проекции траектории поиска на плоскости (z1,z2) и (z3,z4) соответственно. Пунктиром обозначен исходный многогранник. На рис. 4 и 5 представлены графики функций h(z) и e(z) до (пунктир) и после оптимизации. Из приведенных рисунков ясно, что профиль волноводного перехода оказывает большее влияние на характеристики чем заполнение. Из рис. 3 видно, что функционал fa имеет сложную структуру.
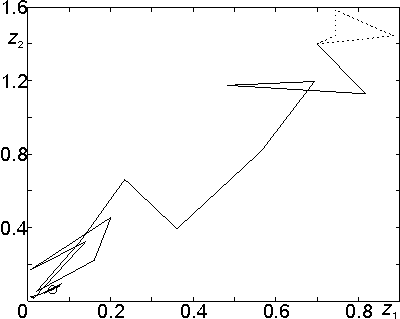
Рис. 2. Проекция траектории поиска на плоскость (z1,z2).
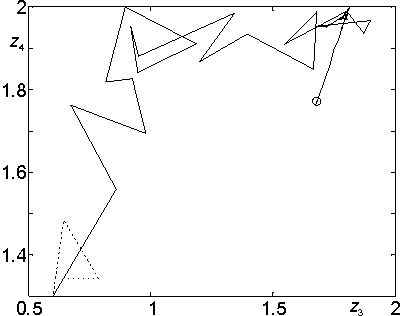
Рис. 3. Проекция траектории поиска на плоскость (z3,z4).
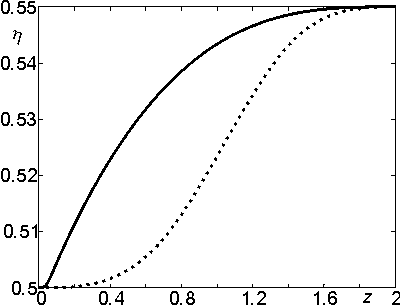
Рис. 4. График функции h до и после
оптимизации.
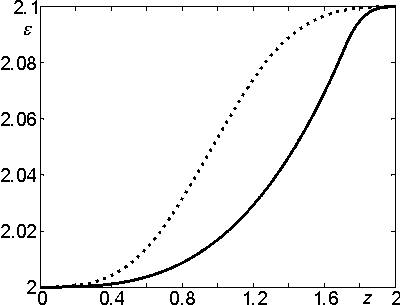
Рис. 5. График функции e до и после
оптимизации.
3. ПЕРЕХОД МЕЖДУ ПРЯМОУГОЛЬНЫМ И КОМПЛАНАРНЫМ ВОЛНОВОДАМИ
В этом разделе исследуется распространение основной ТЕ-моды прямоугольного волновода через переход с согласующим ребром (рис. 6) на компланарный волновод [6].
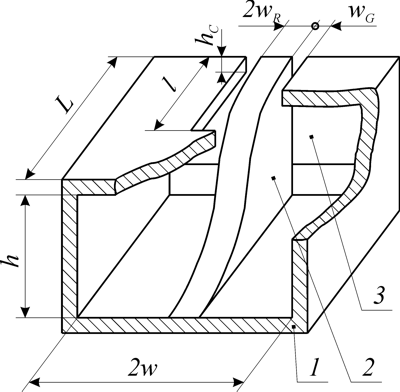
Рис. 6. Геометрия волноводного перехода между прямоугольным и компланарным
волноводами. 1 - входное сечение, 2 - ребро, 3 - выходное
сечение.
Учитывая симметрию поля и перехода можно ограничиться рассмотрением половины данной согласующей системы. Обозначим через u z-компоненту магнитного вектора Герца Pm. Предполагая временную зависимость поля в виде exp(-iwt), приходим к задаче решения однородного уравнения Гельмгольца в ограниченной области D. Все металлические поверхности предполагаются идеально проводящими. Для ограничения области в продольном направлении используются парциальные условия излучения. На плоскости симметрии требуем равенства нулю функции u. Введем декартову систему координат с началом, расположенным в плоскости симметрии перехода на его нижнем основании, ось x направим перпендикулярно плоскости симметрии, а ось z – вдоль оси волноведущей системы. Входное сечение перехода находится в плоскости z=0. Краевая задача принимает вид:
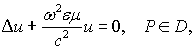 |
(14) |
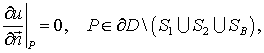 |
(15) |
| (16) | |
| (17) | |
| (18) |
где S1 – входное сечение, S2 – выходное сечение, SB – поверхность с вектором нормали n, имеющим отличную от 0 z-компоненту, e – диэлектрическая проницаемость, m – магнитная восприимчивость, c – скорость света, gn(1,2) – постоянные распространения мод прямоугольного и компланарного волноводов, jn(1,2) – функции сечения входного и выходного волноводов, u0 – падающее поле, Rn – амплитуды отраженных мод, Tn – амплитуды мод, возбужденных в выходном волноводе.
Для решения поставленной краевой задачи (14)-(18) применяется метод конечных элементов. Моды компланарного волновода вычислялись с помощью метода двумерных конечных элементов. Однородное заполнение всего волновода позволяет вычислять моды компланарного волновода только один раз. Моды прямоугольного волновода получены аналитически.
Для построения конечных элементов область D разбивалась на тетраэдры. Носителем базисной функции yn является группа тетраэдров, имеющих общую вершину с индексом n. Использовались линейные базисные функции. В результате получим N базисных функций, где N – количество вершин, в которых функция u может быть отлична от 0. Приближенное решение задачи ищем в конечномерном пространстве, образованном системой функций yn:
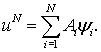 |
(19) |
Записывая уравнение (14) в слабой форме и, применяя к нему теорему Грина, получим уравнение:
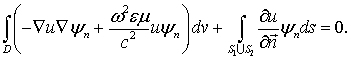 |
(20) |
Для преобразования второго интеграла в уравнении (20) используются условия излучения (17), (18) и проекционные соотношения:
| (21) | |
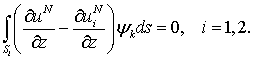 |
(22) |
Здесь uN1,2 выражаются формулами (17) и (18), M1,2 – константы, определяющие количество членов в рядах в этих формулах.
В результате получаем систему линейных алгебраических уравнений размерности N относительно коэффициентов Ai. Для ее решения используется метод минимальной степени, заключающийся в минимизации заполнения на каждом шаге исключения по методу Гаусса [7]. Зная Ai можно найти коэффициенты отражения и пропускания.
В данном случае можно ставить задачу оптимизации как поиск таких параметров перехода, которые обеспечивают, например, максимальную передачу энергии или обеспечивают максимальную амплитуду определенной моды в компланарном волноводе.
Рассмотрим переход, имеющий ребро с профилем в виде ломаной состоящей из трех отрезков, координаты вершин которой являются параметрами оптимизации, и будем для него рассматривать задачу минимизации коэффициента отражения по энергии R. Для ее решения также использовался метод регуляризации А.Н. Тихонова со сглаживающим функционалом:
| (23) |
Стабилизатор W выбран в форме z12+y12+(1–z2)2+(1–y2)2, где zi, yi – относительные координаты вершин ломаной. Ограничения, накладываемые на параметры оптимизации, обусловлены требованием монотонности профиля ребра, а также требованием отсутствия перекрытия с другими частями перехода. В процессе оптимизации параметры изменялись таким образом, что ребро вырождалось в ступеньку, что соответствует выводам сделанным в статье [6].
4. ИССЛЕДОВАНИЕ ЭФФЕКТИВНОСТИ РАСПАРАЛЛЕЛИВАНИЯ МЕТОДА СКОЛЬЗЯЩЕГО ДОПУСКА
Решение задачи оптимизации требует многократного решения прямой задачи расчета характеристик волноводного перехода при различных параметрах, однако в трехмерном случае размерность получаемых систем очень велика и их решение занимает много времени. Метод Нелдера и Мида допускает распараллеливание и, используя вычислительный кластер, можно легко поднять скорость счета, даже не распараллеливая алгоритм решения прямой задачи.
Алгоритм скользящего допуска построен на основе симплекс метода, который заключается в последовательном деформировании многогранника путем замены по определенным правилам его вершины, в которой значение минимизируемого функционала наихудшее, на другую. При выборе новой вершины возникает потребность в вычислении значения функционала один или два раза, но всего имеется 4 возможных варианта новой вершины на каждом шаге вне зависимости от размерности. Кроме того, в случае отсутствия подходящей вершины среди этих четырех, производится пропорциональное уменьшение многогранника относительно вершины с наилучшим значением функционала.
Проведенные исследования на тестовом функционале показали, что, используя 3-4 процессора, можно поднять скорость поиска минимума в два раза. На рис. 7 показана зависимость времени счета от количества использованных процессоров при различной размерности векторов q (Np). Для более сложных функционалов возможно даже большее ускорение. При наличии дополнительных процессоров имеются различные варианты стратегии углубленного поиска, однако тестирование показало, что, по сравнению с равномерным распределением процессоров по вариантам, только некоторые стратегии имеют незначительное преимущество и то, не для любого количества используемых процессоров. Очевидно, что в некоторых частных случаях преимуществом могут обладать те или иные варианты стратегии, однако в общем случае можно использовать равномерное распределение процессоров по вариантам.
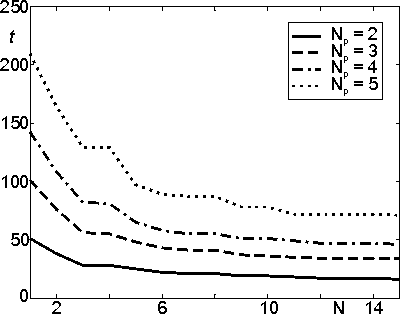
Рис. 7. Время решения в зависимости от количества процессоров.
В случае необходимости решения задачи математического проектирования волноводного перехода, работающего в некотором диапазоне частот, возникает потребность в вычислении характеристик перехода при фиксированных параметрах и нескольких значениях частоты. Поэтому для получения максимальной эффективности от применения кластера нужно одновременно вычислять характеристики перехода при различных частотах, а необходимость в распараллеливании, как алгоритма решения прямой задачи, так и алгоритма решения обратной задачи отпадает.
ЛИТЕРАТУРА