УДК 621.391.01
ВЛИЯНИЕ НЕЛИНЕЙНОСТЕЙ ПЕРЕДАТЧИКА НА
МНОГОЧАСТОТНЫЕ СИГНАЛЫ С ОРТОГОНАЛЬНЫМ ЧАСТОТНЫМ МУЛЬТИПЛЕКСИРОВАНИЕМ
Л. Е. Назаров¹, А. С. Зудилин²
¹Институт радиотехники и электроники им. В.А.Котельникова РАН, г.Фрязино
²ОАО “Российские космические системы”, г. Москва
Получена 9 декабря 2010 г.
Аннотация. Приведены результаты исследований влияния нелинейностей передатчика на эффективность передачи многочастотных сигналов с ортогональным частотным мультиплексированием, характеризуемых высокими значениями пик/фактор.
Ключевые слова: нелинейности передатчика, OFDM сигналы, интермодуляционные помехи, турбо-коды.
Введение
Многочастотные сигналы с ортогональным частотным мультиплексированием рассматриваются как одни из наиболее перспективных сигналов для передачи информации по каналам с многолучевостью [1]. Эти сигналы являются базовыми для ряда принятых протоколов, например, IEEE802.16 [2].
Рассматриваемые сигналы имеют высокие значения отношений пиковой мощности к средней мощности (пик/фактор) [1]. Поэтому при передаче данных сигналов с использованием нелинейных передатчиков возникают искажения амплитуда/амплитуда (АМ/АМ) и амплитуда/фаза (АМ/ФМ), определяющие интермодуляционные помехи и фазовые искажения в дополнение к канальным аддитивным шумам [3]. Исследования этих эффектов проведены для рассматриваемых сигналов без кодирования, а также с использованием с относительно простыми схемами помехоустойчивого кодирования, например, в сочетании со сверточными кодами [4].
В настоящей работе
приведены результаты исследований влияния нелинейностей на передачу данных
сигналов в сочетании со значительно более эффективной по сравнению со
сверточными кодами схемой помехоустойчивого кодирования, входящей в класс
турбо-кодов [5,6]. Исследования произведены путем моделирования процедуры
обработки сигналов при их приеме с использованием моделей нелинейных амплитудных
и фазовых искажений передатчиков на основе лампы бегущей волны.
1. Постановка задачи
Многочастотные сигналы с ортогональным частотным
мультиплексированием, известные в литературе также как OFDM сигналы (orthogonal frequency-division multiplexing) [1,2], представляют
сумму ![]() гармонических парциальных сигналов с
различными “созвездиями”
гармонических парциальных сигналов с
различными “созвездиями”
![]() при их
модуляции и с различными несущими частотами
при их
модуляции и с различными несущими частотами ![]() . Спектры этих сигналов
пересекаются в общей полосе, поэтому они характеризуются большей частотной
эффективностью по отношению к ортогональным сигналам с частотным разделением, не
имеющих пересечения спектров.
. Спектры этих сигналов
пересекаются в общей полосе, поэтому они характеризуются большей частотной
эффективностью по отношению к ортогональным сигналам с частотным разделением, не
имеющих пересечения спектров.
Формирование
OFDM сигналов
производится следующим образом. На основе последовательности двоичных кодовых
символов объемом ![]() , поступающей с
выхода кодера помехоустойчивого кода на вход модулятора сигналов, формируется блок из
, поступающей с
выхода кодера помехоустойчивого кода на вход модулятора сигналов, формируется блок из ![]() комплексных символов {
комплексных символов {![]() }, которые определяют
комплексную огибающую OFDM
сигналов
}, которые определяют
комплексную огибающую OFDM
сигналов
Здесь
![]() принимает одно
из
принимает одно
из ![]() возможных значений из сигнального
“созвездия”
возможных значений из сигнального
“созвездия” ![]() ,
, ![]() .
.
Ортогональность парциальных сигналов обеспечивается
выбором значения частот ![]() для двумерных сигналов (“созвездия”
многофазовой модуляции ФМ-М или квадратурной фазовой модуляции QAM-М) и
для двумерных сигналов (“созвездия”
многофазовой модуляции ФМ-М или квадратурной фазовой модуляции QAM-М) и ![]() для одномерных сигналов (“созвездия
двухфазовой модуляции ФМ-2) [1]. Здесь
для одномерных сигналов (“созвездия
двухфазовой модуляции ФМ-2) [1]. Здесь ![]() - длительность сигналов.
- длительность сигналов.
Важным параметром
радиосигналов является пик/фактор
![]() , где
, где ![]() -
средняя мощность радиосигналов [3]. Пик/фактор
-
средняя мощность радиосигналов [3]. Пик/фактор ![]() определяет динамический
диапазон радиосигналов и при его высоком значении необходимо снижать выходную
мощность передатчика с нелинейностями относительно номинального значения с целью
уменьшения интермодуляционных помех и внеполосных излучений до требуемых
значений.
определяет динамический
диапазон радиосигналов и при его высоком значении необходимо снижать выходную
мощность передатчика с нелинейностями относительно номинального значения с целью
уменьшения интермодуляционных помех и внеполосных излучений до требуемых
значений.
Исследуемые
OFDM сигналы характеризуются
высокими значениями пик/фактора - для “созвездий” с постоянной мощностью верно
соотношение ![]() [1]. Это является
недостатком данных сигналов по отношению к сигналам с постоянной огибающей.
Поэтому актуальной является проблема исследования влияния нелинейностей
передатчика на OFDM сигналы в совокупности со схемами
помехоустойчивого кодирования, в частности, с наиболее эффективными кодами,
обеспечивающими практически предельные вероятностные характеристики при передаче
информации. В качестве подобной схемы кодирования ниже рассмотрен турбо-код,
описание его структуры приведены в работе [6].
[1]. Это является
недостатком данных сигналов по отношению к сигналам с постоянной огибающей.
Поэтому актуальной является проблема исследования влияния нелинейностей
передатчика на OFDM сигналы в совокупности со схемами
помехоустойчивого кодирования, в частности, с наиболее эффективными кодами,
обеспечивающими практически предельные вероятностные характеристики при передаче
информации. В качестве подобной схемы кодирования ниже рассмотрен турбо-код,
описание его структуры приведены в работе [6].
2. Описание сигнально-кодовых конструкций и процедуры их обработки при приеме
Рассматриваемый турбо-код формируется на основе
объединения двух кодов - внешнего и внутреннего кодов ![]() и
и ![]() . Его особенностью является то, что
составляющие коды входят в класс простейших блоковых кодов, что обусловливает
низкую сложность результирующего алгоритма приема по отношению к алгоритмам
приема известных в литературе турбо-кодов [5]. Блок-схеме кодера
рассматриваемого турбо-кода, приведена на рис.1.
. Его особенностью является то, что
составляющие коды входят в класс простейших блоковых кодов, что обусловливает
низкую сложность результирующего алгоритма приема по отношению к алгоритмам
приема известных в литературе турбо-кодов [5]. Блок-схеме кодера
рассматриваемого турбо-кода, приведена на рис.1.
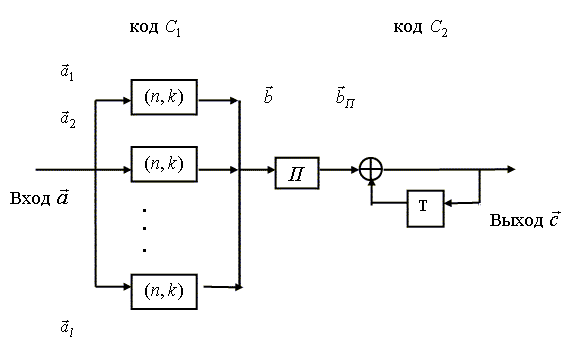
Рис.1. Блок-схема кодера турбо-кода на основе рекурсивного сверточного
кода с двумя состояниями кодовой решетки (Т – элемент задержки на такт, ![]() - перемежитель).
- перемежитель).
Код ![]() включает
включает
![]() идентичных
блоковых кодов
идентичных
блоковых кодов ![]() . Здесь
. Здесь ![]() - длительность кодовых
слов,
- длительность кодовых
слов,
![]() - объем
информационного блока. В качестве составляющего кода в составе кода
- объем
информационного блока. В качестве составляющего кода в составе кода ![]() используется блоковый
биортогональный код с параметрами (7,3).
используется блоковый
биортогональный код с параметрами (7,3).
В качестве внутреннего
кода ![]() используется блоковый код
используется блоковый код ![]() , эквивалентный
усеченному рекурсивному сверточному коду с кодовой скоростью 1 и длиной кодового
ограничения 1 (число состояний кодовой решетки равно 2).
, эквивалентный
усеченному рекурсивному сверточному коду с кодовой скоростью 1 и длиной кодового
ограничения 1 (число состояний кодовой решетки равно 2).
При моделировании
задавались параметры турбо-кода:
![]() .
Информационный объем турбо-кода равен
.
Информационный объем турбо-кода равен ![]() битов, длительность кодовых слов равна
битов, длительность кодовых слов равна ![]() символов, кодовая скорость равна 3/7.
символов, кодовая скорость равна 3/7.
На вход канала
поступает вещественная реализация ![]() , где
, где
![]() - центральная
частота радиосигналов,
- центральная
частота радиосигналов,
![]() - функция
нелинейности передатчика. Для используемого при исследовании двумерного
сигнального “созвездия” ФМ-4 длительность последовательности комплексных
символов, определяющая
комплексную огибающую OFDM
сигналов
- функция
нелинейности передатчика. Для используемого при исследовании двумерного
сигнального “созвездия” ФМ-4 длительность последовательности комплексных
символов, определяющая
комплексную огибающую OFDM
сигналов
![]() (1), равна
(1), равна ![]() .
.
В приемном устройстве
осуществляется обработка реализации ![]() с выхода канала с
аддитивным белым гауссовским шумом
с выхода канала с
аддитивным белым гауссовским шумом ![]() (АБГШ канал) и принимается решение
относительно
переданной информационной последовательности. Обработка содержит два этапа. На первом этапе на
основе
(АБГШ канал) и принимается решение
относительно
переданной информационной последовательности. Обработка содержит два этапа. На первом этапе на
основе ![]() производятся оценки “мягких”
решений комплексных символов {
производятся оценки “мягких”
решений комплексных символов {![]() } в соответствии с правилом
} в соответствии с правилом
Здесь ![]() - комплексная амплитуда реализации
- комплексная амплитуда реализации ![]() .
.
При цифровой реализации процедур формирования OFDM сигналов (1) и при оценке “мягких” решений (2) применяется производительная процедура быстрого спектрального преобразования в базисе Фурье [1,2].
На втором этапе на основе “мягких” решений {![]() } и априорных вероятностей кодовых символов реализуется прием
рассматриваемого турбо-кода. Алгоритм приема итеративный [5,6], суть которого -
вычисление отношений правдоподобия для апостериорных вероятностей символов
кодовых слов турбо-кода и ее представление в виде суммы трех составляющих,
связанных с решениями
} и априорных вероятностей кодовых символов реализуется прием
рассматриваемого турбо-кода. Алгоритм приема итеративный [5,6], суть которого -
вычисление отношений правдоподобия для апостериорных вероятностей символов
кодовых слов турбо-кода и ее представление в виде суммы трех составляющих,
связанных с решениями ![]() , с отношениями априорных вероятностей символов кодовых слов и с
функционалами от отношений апостериорных вероятностей символов (extrinsic information) (EI)
[6]. Для последующей итерации величины EI
используются как априорные вероятности символов кодовых слов.
, с отношениями априорных вероятностей символов кодовых слов и с
функционалами от отношений апостериорных вероятностей символов (extrinsic information) (EI)
[6]. Для последующей итерации величины EI
используются как априорные вероятности символов кодовых слов.
3. Модели нелинейностей
Рассмотрим принятые в
литературе модели нелинейностей передатчика АМ/АМ и АМ/ФМ. Для входного
узкополосного сигнала с комплексной амплитудой ![]() комплексная амплитуда
сигнала с выхода передатчика, рассматриваемого как неинерционное нелинейное
устройство, имеет вид [7]
комплексная амплитуда
сигнала с выхода передатчика, рассматриваемого как неинерционное нелинейное
устройство, имеет вид [7]
![]() . (2')
. (2')
Здесь ![]() - нелинейности АМ/АМ и
АМ/ФМ.
- нелинейности АМ/АМ и
АМ/ФМ.
Для передатчиков на основе
лампы бегущей волны (ЛБВ) модельные нормализованные представления
![]() имеют вид [7]
имеют вид [7]
В точке насыщения при ![]() имеем
имеем
![]() .
.
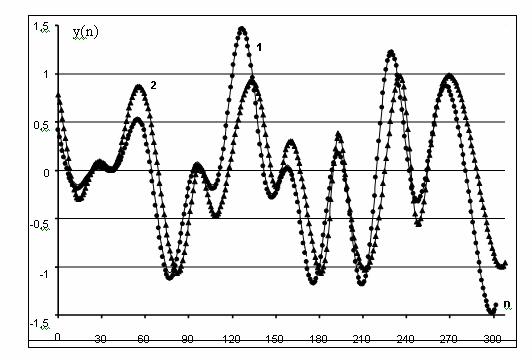
Рис.2. Фрагменты дискретизированного
OFDM сигнала на входе ЛБВ (кривая 1) и на
выходе ЛБВ (кривая 2) (![]() , “созвездие” ФМ-4).
, “созвездие” ФМ-4).
В качестве примера на
рис.2 приведены фрагменты дискретизированного
OFDM сигнала на входе ЛБВ и на ее выходе.
Видны отличия кривых за счет влияния нелинейностей (3). На рис.3 приведены
вероятностные кривые (зависимость вероятности ошибки на бит
![]() от отношения
от отношения ![]() ), полученные путем моделирования приема OFDM сигналов при передаче по АБГШ каналу. Здесь
), полученные путем моделирования приема OFDM сигналов при передаче по АБГШ каналу. Здесь
![]() - энергия
сигналов на бит,
- энергия
сигналов на бит, ![]() - односторонняя спектральная плотность
шума. Кривая 1 соответствует передаче OFDM сигналов без кодирования по линейному
каналу (
- односторонняя спектральная плотность
шума. Кривая 1 соответствует передаче OFDM сигналов без кодирования по линейному
каналу (![]() , “созвездие” ФМ-4), кривая 2 получена для
данных сигналов, передаваемых по каналу с нелинейностями (3). В этом случае
влияние нелинейностей приводит к существенному ухудшению помехоустойчивости.
, “созвездие” ФМ-4), кривая 2 получена для
данных сигналов, передаваемых по каналу с нелинейностями (3). В этом случае
влияние нелинейностей приводит к существенному ухудшению помехоустойчивости.
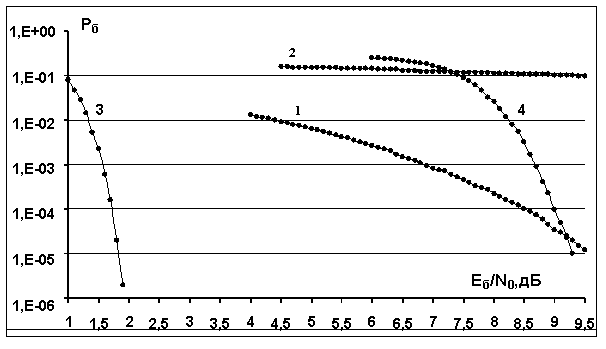
Рис.3. Вероятностные кривые OFDM сигналов при передаче по АБГШ каналу: 1 - линейный
канал (![]() , “созвездие” ФМ-4 без кодирования), 2 -
канал с нелинейностями (
, “созвездие” ФМ-4 без кодирования), 2 -
канал с нелинейностями (![]() ,
“созвездие” ФМ-4 без кодирования), 3 – линейный канал (
,
“созвездие” ФМ-4 без кодирования), 3 – линейный канал (![]() , “созвездие” ФМ-4, турбо-код с
кодовой скоростью 3/7), 4 – канал с нелинейностями (
, “созвездие” ФМ-4, турбо-код с
кодовой скоростью 3/7), 4 – канал с нелинейностями (![]() , “созвездие” ФМ-4, турбо-код с кодовой скоростью 3/7).
, “созвездие” ФМ-4, турбо-код с кодовой скоростью 3/7).
Кривые 3,4 на рис.3 соответствуют аналогичным вероятностным кривым для OFDM сигналов в совокупности с рассматриваемым турбо-кодом. Кривая 3 получена для линейного канала, кривая 4 получена для канала с нелинейностями (3) (“созвездие” ФМ-4). Энергетические потери для канала с нелинейностями по отношению к линейному каналу превышают 7 дБ.
Известные методы борьбы с нелинейностями основаны на линеаризации каналов, а также на снижении мощности OFDM сигналов на входе передатчика с целью его работы в режиме, близком к линейному режиму.
Суть методов линеаризации
- искажение сигналов на входе передатчика
![]() с целью
компенсации амплитудной и фазовой нелинейностей. Для этого необходимо, чтобы
функции
с целью
компенсации амплитудной и фазовой нелинейностей. Для этого необходимо, чтобы
функции
![]() являлись
решениями системы уравнений [7]
являлись
решениями системы уравнений [7]
![]() , (4)
, (4)
![]() . (5)
. (5)
Разработаны методы решения
системы (4), (5) [4,7]. В работе [4] приведены методы линеаризации, основу
которых составляют решения данной системы с
использованием приближения функции
![]() к аппроксимирующей
функции
к аппроксимирующей
функции ![]() . В качестве аппроксимирующей функции
. В качестве аппроксимирующей функции ![]() в [4] использовалось симметричное
ограничение с зоной линейности
в [4] использовалось симметричное
ограничение с зоной линейности
Функция
![]() соответствовала
решению системы (4), (5). В этом случае снижение мощности входных сигналов на
соответствовала
решению системы (4), (5). В этом случае снижение мощности входных сигналов на ![]() (дБ) соответствует близкому к
линейному снижению мощности выходного сигнала на
(дБ) соответствует близкому к
линейному снижению мощности выходного сигнала на ![]() (дБ), что определяет увеличение
вероятности ошибки при приеме. Вместе с тем, снижается мощность интермодуляционных
помех. Поэтому существует оптимальное значение
(дБ), что определяет увеличение
вероятности ошибки при приеме. Вместе с тем, снижается мощность интермодуляционных
помех. Поэтому существует оптимальное значение ![]() (оптимальное значение
(оптимальное значение ![]() ), определяющее достижение
минимальной вероятности ошибки
), определяющее достижение
минимальной вероятности ошибки ![]() . Снижение эффективности передатчика при
генерации
OFDM сигналов по отношению к сигналам с
постоянной огибающей, при генерации которых передатчик работает в режиме
насыщения (
. Снижение эффективности передатчика при
генерации
OFDM сигналов по отношению к сигналам с
постоянной огибающей, при генерации которых передатчик работает в режиме
насыщения (![]() =0 дБ), можно оценить
соотношением
=0 дБ), можно оценить
соотношением
![]() =
=![]() . Здесь
. Здесь ![]() - увеличение мощности сигнала, требуемое
для компенсации интермодуляционных помех при значении
- увеличение мощности сигнала, требуемое
для компенсации интермодуляционных помех при значении ![]() и достижения задаваемой
вероятности
и достижения задаваемой
вероятности ![]() для линейного канала
(при моделировании задавалось значение
для линейного канала
(при моделировании задавалось значение ![]() .
.
Теоретическому анализу
интермодуляционных помех и оцениванию значений ![]() при использовании
аппроксимирующих функций
при использовании
аппроксимирующих функций ![]() в виде симметричного ограничения с зоной
линейности и предельного симметричного ограничения без зоны нелинейности
посвящен ряд работ,
например [3,8]. В работе [3] приведены аналитические выражения для мощности
интермодуляционных помех и оценки
в виде симметричного ограничения с зоной
линейности и предельного симметричного ограничения без зоны нелинейности
посвящен ряд работ,
например [3,8]. В работе [3] приведены аналитические выражения для мощности
интермодуляционных помех и оценки
![]() при
использовании функции
при
использовании функции ![]() для ансамблей ортогональных сигналов, входящих в класс
сигналов с частотным разделением. В работе [8] рассмотрено влияние нелинейности
в виде предельного симметричного ограничителя без зоны линейности на сумму
гармонического сигнала и сильного гауссовского сигнала, одномерная плотность
амплитуды огибающей которого распределена по закону Рэлея. Показано, что в этом
случае выполняется соотношение
для ансамблей ортогональных сигналов, входящих в класс
сигналов с частотным разделением. В работе [8] рассмотрено влияние нелинейности
в виде предельного симметричного ограничителя без зоны линейности на сумму
гармонического сигнала и сильного гауссовского сигнала, одномерная плотность
амплитуды огибающей которого распределена по закону Рэлея. Показано, что в этом
случае выполняется соотношение ![]() /
/![]()
![]() 9.35 дБ на краях полосы сигналов и
9.35 дБ на краях полосы сигналов и ![]() /
/![]()
![]() 7.8 дБ в центре полосы сигналов с точностью
до 1 дБ. Здесь
7.8 дБ в центре полосы сигналов с точностью
до 1 дБ. Здесь ![]() - мощность интермодуляционных
помех в полосе сигналов,
- мощность интермодуляционных
помех в полосе сигналов, ![]() - мощность выходного
гармонического сигнала.
- мощность выходного
гармонического сигнала.
При теоретическом
оценивании мощности интермодуляционных помех ![]() и значений
и значений ![]() для OFDM сигналов и рассматриваемых функций
для OFDM сигналов и рассматриваемых функций ![]() данные методики также можно применять.
данные методики также можно применять.
4. Анализ результатов моделирования
На рис.4 приведены
значения отношения сигнал/помеха
![]() (дБ) для
парциальных сигналов при использовании предельного симметричного ограничителя
без зоны линейности (OFDM без кодирования,
(дБ) для
парциальных сигналов при использовании предельного симметричного ограничителя
без зоны линейности (OFDM без кодирования, ![]() , “созвездие” ФМ-4). Здесь
, “созвездие” ФМ-4). Здесь ![]() - мощность выходного парциального сигнала,
- мощность выходного парциального сигнала, ![]() - мощность интермодуляционной
помехи в полосе парциального сигнала с номером
- мощность интермодуляционной
помехи в полосе парциального сигнала с номером ![]() . Значения
. Значения
![]() получены путем обработки искаженных OFDM сигналов с выхода нелинейного элемента.
получены путем обработки искаженных OFDM сигналов с выхода нелинейного элемента.
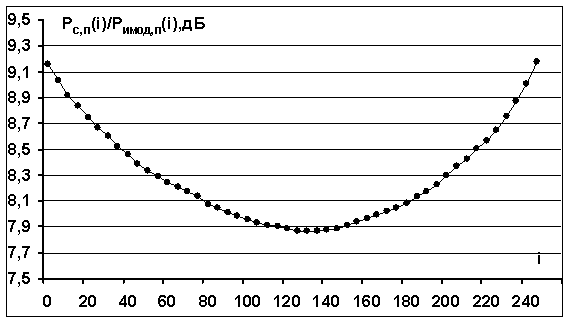
Рис.4. Зависимость отношения
сигнал/помеха
![]() парциальных
сигналов от их номера
парциальных
сигналов от их номера ![]() , соответствующие предельному
симметричному ограничению без зоны линейности (
, соответствующие предельному
симметричному ограничению без зоны линейности (![]() , “созвездие” ФМ-4).
, “созвездие” ФМ-4).
Оценивание значений ![]() осуществлялось в соответствие с
методикой, приведенной в [8]. Оценивание суммарной мощности
осуществлялось в соответствие с
методикой, приведенной в [8]. Оценивание суммарной мощности ![]() +
+![]() производилось при помощи свертки
искаженного
OFDM сигнала с выхода нелинейного элемента
с данным парциальным сигналом с номером
производилось при помощи свертки
искаженного
OFDM сигнала с выхода нелинейного элемента
с данным парциальным сигналом с номером ![]() . При этом полагался малым вклад в суммарную
мощность за счет корреляции парциального сигнала и интермодуляционных помех.
Оценивание мощности интермодуляционной помехи
. При этом полагался малым вклад в суммарную
мощность за счет корреляции парциального сигнала и интермодуляционных помех.
Оценивание мощности интермодуляционной помехи ![]() производилось при отсутствии парциального
сигнала с номером
производилось при отсутствии парциального
сигнала с номером ![]() при помощи свертки искаженного OFDM сигнала с выхода нелинейного элемента
с базисной функцией
при помощи свертки искаженного OFDM сигнала с выхода нелинейного элемента
с базисной функцией ![]() .
.
Поведение кривой на рис.4
согласуется с результатами теоретического анализа - наблюдается повышение
рассматриваемого отношения сигнал/помеха на краях полосы сигналов (![]() дБ) и понижение в центре полосы сигналов (
дБ) и понижение в центре полосы сигналов (![]() дБ). Различие приведенных
значений сигнал/помеха достигает 1.36 дБ, что практически совпадает с
приведенной выше теоретической оценкой данных величин. Объяснение этому
заключается в том, что OFDM сигнал при большом количестве парциальных сигналов (
дБ). Различие приведенных
значений сигнал/помеха достигает 1.36 дБ, что практически совпадает с
приведенной выше теоретической оценкой данных величин. Объяснение этому
заключается в том, что OFDM сигнал при большом количестве парциальных сигналов (![]() ) можно рассматривать как
гауссовский сигнал [9]. В этом случае для
OFDM сигнала справедлива модель суммы
гармонического парциального сигнала и сильного гауссовского сигнала, для анализа
интермодуляционных помех этой модели можно применить рассмотренную методику [8].
) можно рассматривать как
гауссовский сигнал [9]. В этом случае для
OFDM сигнала справедлива модель суммы
гармонического парциального сигнала и сильного гауссовского сигнала, для анализа
интермодуляционных помех этой модели можно применить рассмотренную методику [8].
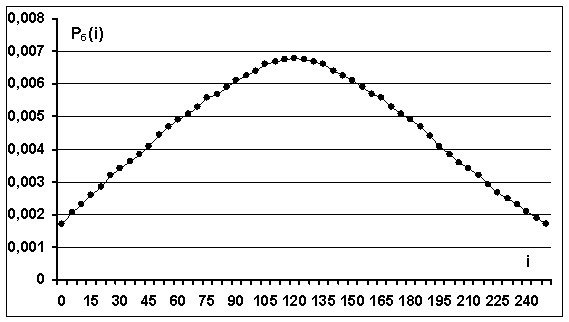
Рис.5. Зависимость вероятности ![]() ошибочного приема битов
парциального сигнала с номером
ошибочного приема битов
парциального сигнала с номером ![]() для OFDM сигналов без кодирования и с
использованием нелинейной функции предельного симметричного ограничения без зоны
линейности
(
для OFDM сигналов без кодирования и с
использованием нелинейной функции предельного симметричного ограничения без зоны
линейности
(![]() , “созвездие” ФМ-4).
, “созвездие” ФМ-4).
На рис.5 приведена
зависимость вероятности ![]() ошибочного приема битов
парциального сигнала с номером
ошибочного приема битов
парциального сигнала с номером ![]() для рассмотренного ансамбля OFDM сигналов без кодирования и с
использованием предельного симметричного
ограничения без зоны линейности. Данная зависимость
получена получена путем моделирования. Видно, что значения
для рассмотренного ансамбля OFDM сигналов без кодирования и с
использованием предельного симметричного
ограничения без зоны линейности. Данная зависимость
получена получена путем моделирования. Видно, что значения ![]() максимальны в центре
полосы сигналов
максимальны в центре
полосы сигналов ![]() и минимальны на краях полосы
и минимальны на краях полосы ![]() . Поведение данной вероятностной кривой
согласуется с кривой
. Поведение данной вероятностной кривой
согласуется с кривой ![]() на рис.4. Для сигнального
“созвездия” ФМ-4 выполняется соотношение
на рис.4. Для сигнального
“созвездия” ФМ-4 выполняется соотношение ![]() . С учетом этого
вычислены теоретические вероятности ошибки
. С учетом этого
вычислены теоретические вероятности ошибки ![]() для величины
для величины ![]() дБ в центре полосы и
дБ в центре полосы и ![]() дБ на краях полосы, равные
дБ на краях полосы, равные ![]() и
и ![]() соответственно. Эти значения вероятностей
практически совпадают со значениями, полученными при моделировании.
соответственно. Эти значения вероятностей
практически совпадают со значениями, полученными при моделировании.
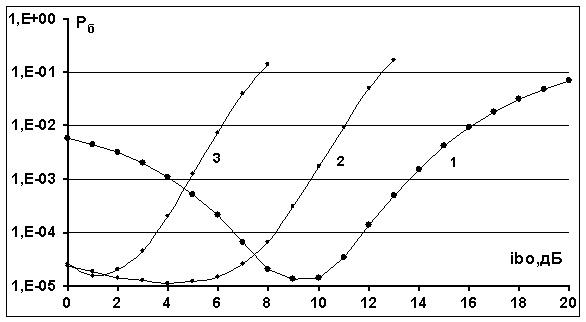
Рис.6. Вероятностные кривые для
сигнально-кодовых конструкций при изменении параметра ![]() : 1 - OFDM сигналы без кодирования; 2 - OFDM сигналы со сверточным кодом с кодовой скоростью 1/2; 3
- OFDM сигналы с турбо-кодом с кодовой
скоростью 3/7.
: 1 - OFDM сигналы без кодирования; 2 - OFDM сигналы со сверточным кодом с кодовой скоростью 1/2; 3
- OFDM сигналы с турбо-кодом с кодовой
скоростью 3/7.
На рис.6 приведены
зависимости вероятности ошибки
![]() при изменении
параметра
при изменении
параметра ![]() , полученные путем
моделирования соответствующих алгоритмов приема для ряда сигнально-кодовых
конструкций на основе OFDM сигналов при использовании
симметричного ограничения
с зоной линейности (6). Кривая 1 соответствует
приему
OFDM сигналов без кодирования (
, полученные путем
моделирования соответствующих алгоритмов приема для ряда сигнально-кодовых
конструкций на основе OFDM сигналов при использовании
симметричного ограничения
с зоной линейности (6). Кривая 1 соответствует
приему
OFDM сигналов без кодирования (![]() , “созвездие” ФМ-4).
Видно, что
, “созвездие” ФМ-4).
Видно, что ![]() дБ, при этом вероятность ошибки
дБ, при этом вероятность ошибки ![]() достигается при значении
достигается при значении ![]() дБ. То есть для данной
конструкции снижение эффективности передатчика при генерации
OFDM сигналов по отношению к сигналам с
постоянной огибающей оценивается значением
дБ. То есть для данной
конструкции снижение эффективности передатчика при генерации
OFDM сигналов по отношению к сигналам с
постоянной огибающей оценивается значением ![]() дБ.
дБ.
Кривая 2 соответствует
приему
OFDM сигналов в сочетании со сверточным
кодом с кодовой скоростью 1/2 (![]() , “созвездие” ФМ-4). В
этом случае значение
, “созвездие” ФМ-4). В
этом случае значение ![]() равно
равно ![]() дБ, при этом вероятность ошибки
дБ, при этом вероятность ошибки ![]() достигается при значении
достигается при значении ![]() дБ. Для данной
сигнальной конструкции снижение эффективности передатчика при генерации
OFDM сигналов по отношению к сигналам с
постоянной огибающей оценивается значением
дБ. Для данной
сигнальной конструкции снижение эффективности передатчика при генерации
OFDM сигналов по отношению к сигналам с
постоянной огибающей оценивается значением ![]() дБ.
дБ.
Кривая 3 соответствует
приему
OFDM сигналов в сочетании с
рассматриваемым турбо-кодом с кодовой скоростью 3/7 (“созвездие” ФМ-4). В этом
случае оптимальное значение равно
![]() дБ, при этом вероятность ошибки
дБ, при этом вероятность ошибки ![]() достигается при значении
достигается при значении ![]() дБ. Для данной
сигнальной конструкции на основе турбо-кода снижение эффективности передатчика
при генерации
OFDM сигналов по отношению к сигналам с
постоянной огибающей оценивается значением
дБ. Для данной
сигнальной конструкции на основе турбо-кода снижение эффективности передатчика
при генерации
OFDM сигналов по отношению к сигналам с
постоянной огибающей оценивается значением ![]() дБ.
дБ.
Заключение
Приведены результаты исследований по оцениванию влияния нелинейностей передатчика типа АМ/АМ, АМ/ФМ на передачу сигнально-кодовых конструкций на основе многочастотных сигналов с ортогональным частотным мультиплексированием в сочетании с сигнальным “созвездием” ФМ-4 и со схемами помехоустойчивого кодирования. При теоретическом анализе интермодуляционных помех для искаженных OFDM сигналов на выходе симметричного ограничения с зоной линейности и предельного симметричного ограничения без зоны нелинейности можно применять известные методики, разработанные для сигналов с частотным разделением.
Рассмотрена схема помехоустойчивого кодирования, входящая в класс турбо-кодов и более эффективная по сравнению со сверточными кодами. Путем моделирования алгоритмов приема для линеаризованного канала на основе функции амплитудной нелинейности в виде симметричного ограничения с зоной линейности показано, что снижение эффективности передатчика при генерации OFDM сигналов в сочетании с турбо-кодом по отношению к сигналам с постоянной огибающей не превышает 2.05 дБ. Это значение меньше на 0.7 дБ по отношению к сигнальным конструкциям на основе сверточных кодов с эквивалентной кодовой скоростью и меньше на 2.85 дБ по отношению к сигнальной конструкции без кодирования.
Литература
1. Hara S., Prasad R. Multicarrier Techniques for 4G Mobile Communications. Artech House. Boston. 2003.
2. Liu H., Li G. OFDM-Based Broadband Wireless Networks. A John Wiley & Sons. New Jersey. 2005.
3. Тепляков И.М., Рощин Б.В., Фомин А.И., Вейцель В.А. Радиосистемы передачи информации. М.: Радио и связь. 1982.
4. Benedetto M-G.D., Mandarini P. An Application of MMSE Predistortion to OFDM Systems.// IEEE Transactions on Communications. 1996. Vol.44. N11. P.1417-1420.
5. Solemani M.R., Gao Y., Vilaipornsawai U. Turbo Coding for Satellite and Wireless Communications. New York. Kluwer Academic Publishers. 2002. 214 p.
6. Назаров Л.Е., Головкин И.В. Последовательные турбо-коды с пониженной сложностью алгоритмов приема.// Радиотехника и электроника. 2010. №10. С.1193-1199.
7. Saleh A.A.M., Salz J. Adaptive Linearization of Power Amplifiers in Digital Radio Systems.// The Bell System Technical Journal. 1983. Vol.62. N4. P.1019-1033.
8. Спилкер Дж. Цифровая спутниковая связь. Пер. с англ. М.:Связь. 1979.
9. Гоноровский И.С. Радиотехнические цепи и сигналы. М.: Радио и связь. 1986.
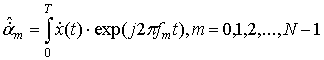 . (2)
. (2)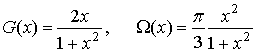 . (3)
. (3)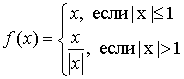 . (6)
. (6)