УДК 621.391
УВЕЛИЧЕНИЕ ОТНОШЕНИЯ СИГНАЛ/ШУМ МЕТОДОМ ПОСЛЕДОВАТЕЛЬНОГО ВЫЧИСЛЕНИЯ АВТОКОРРЕЛЯЦИОННОЙ ФУНКЦИИ
С. А. Останин
Алтайский государственный университет, г. Барнаул
Получена 30 ноября 2011 г.
Аннотация. В работе предложен метод увеличения отношения сигнал/шум сигнала основанный на последовательном вычислении автокорреляционной функции. Метод позволяет повысить отношение сигнал/шум гармонических и периодических негармонических сигналов. Приведены результаты работы обнаружителя сигнала построенного с использованием LabVIEW.
Ключевые слова: обнаружение слабых сигналов, автокорреляционный анализ.
Abstract. In this paper we propose a method of increasing the signal / noise signal based on the sequential calculation of the autocorrelation function. The method allows to improve the signal / noise ratio of harmonic and periodic non-harmonic signals. The results of the detector signal is constructed using LabVIEW.
Keywords: detection of low signals, autocorrelation analysis.
Для обнаружения слабых сигналов в аддитивной смеси с шумом используют, например, корреляционные методы анализа сигнала [1]. В частности, при измерении частоты доплеровских сигналов лазерных анемометров, для оценки скорости движения частиц аэрозоля, с целью увеличения отношения сигнал/шум вычисляют автокорреляционную функцию сигнала [2-3]. Поступающий с фотоприемного устройства сигнал проходит через фильтр высоких частот и при этом теряет постоянную составляющую. Частоту среза выбирают заведомо ниже минимально возможной частоты доплеровского сигнала с тем, чтобы не потерять информацию о скорости движения отражающих объектов. Процессор вычисляет автокорреляционную функцию доплеровского сигнала и по периоду этой функции судят о частоте доплеровского сигнала. Увеличение отношения сигнал/шум зависит, в том числе от длительности сигнала. В тех случаях, когда длительности сигнала увеличить не представляется возможным (например, доплеровские сигналы лазерных анемометров), возникает проблема поиска альтернативных методов повышения отношения сигнал/шум.
Для обнаружения и анализа сигналов такого рода предлагается использовать метод последовательного вычисления автокорреляционной функции, заключающийся в том, что после вычисления автокорреляционной функции исходного сигнала вычисляется автокорреляционная функция от автокорреляционной функции и так далее. При этом отношение с/ш растет от итерации к итерации. Процесс повторяется до тех пор, пока отношение с/ш становится достаточным для определения частоты доплеровского сигнала.
Рассмотрим применение метода для повышения отношения с/ш для гармонического сигнала. Пусть исходный сигнал x(t) представляет собой аддитивную смесь периодического детерминированного сигнала s(t) и шума n(t), являющегося стационарным процессом второго порядка:
Дополнительно предположим, что функции s(t) и n(t) – центрированы. Автокорреляционная функция для сигнала x(t), по определению, вычисляется следующим образом:
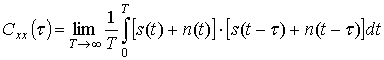 .
.
Отсюда, оценка автокорреляционной функции, в силу дистрибутивности корреляционного оператора, есть
![]() .
.
При условии независимости сигнала s(t) от шума n(t),
корреляционные функции ![]() и
и ![]() тождественно
равны нулю с точностью до погрешностей оценок, обусловленных конечным временем
интегрирования. Автокорреляционная функция шума
тождественно
равны нулю с точностью до погрешностей оценок, обусловленных конечным временем
интегрирования. Автокорреляционная функция шума ![]() стремится к нулю с возрастанием
задержки
стремится к нулю с возрастанием
задержки ![]() и для достаточно больших значений,
больших по модулю некоторого времени задержки
и для достаточно больших значений,
больших по модулю некоторого времени задержки ![]() ,
, ![]() =0. Значение
=0. Значение ![]() ,
начиная с которого автокорреляционную функцию
,
начиная с которого автокорреляционную функцию ![]() можно
положить равной нулю, зависит от характеристик шума, в частности, от его
спектральной плотности: чем шире полоса частот шума при заданной полной
мощности, тем быстрее убывает автокорреляционная функция. И так,
можно
положить равной нулю, зависит от характеристик шума, в частности, от его
спектральной плотности: чем шире полоса частот шума при заданной полной
мощности, тем быстрее убывает автокорреляционная функция. И так,
![]() , (2)
, (2)
где ошибка ![]() тем
меньше, чем больше время интегрирования Т. Фурье-образ
автокорреляционной функции
тем
меньше, чем больше время интегрирования Т. Фурье-образ
автокорреляционной функции ![]() представляет собой спектр мощности и поэтому равен квадрату
Фурье-образа самой функции s(t). А это значит, что автокорреляционная функция содержит все
частоты функции s(t), и только эти частоты. Если, например, x(t) –
сигнал фотоприемника доплеровского анемометра, то частота сигнала равна частоте
его автокорреляционной функции
представляет собой спектр мощности и поэтому равен квадрату
Фурье-образа самой функции s(t). А это значит, что автокорреляционная функция содержит все
частоты функции s(t), и только эти частоты. Если, например, x(t) –
сигнал фотоприемника доплеровского анемометра, то частота сигнала равна частоте
его автокорреляционной функции ![]() . Если обозначить
отношение с/ш до вычисления автокорреляции Rе,
а после вычисления – Rs , то увеличение отношения с/ш по
мощности, для гармонического сигнала s(t) определяется [2] формулой:
. Если обозначить
отношение с/ш до вычисления автокорреляции Rе,
а после вычисления – Rs , то увеличение отношения с/ш по
мощности, для гармонического сигнала s(t) определяется [2] формулой:
G = Rs / Rе ≈ 2ТВ / (2+1/Rе) .
Если Rе<< 1 , то
G = Rs / Rе ≈ 2ТВRе , (3)
Rs ≈ 2ТВR2е . (4)
Далее, введем обозначения
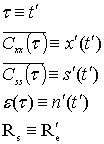 (5)
(5)
поскольку периодическая составляющая
содержится в функции ![]() , а шум – в функции
, а шум – в функции ![]() . Функция
. Функция ![]() ,
также как и
,
также как и ![]() , является центрированной случайной
стационарной функцией, отличающейся от
, является центрированной случайной
стационарной функцией, отличающейся от ![]() тем,
что имеет меньшую дисперсию. Следовательно, можно вычислить автокорреляционную
функцию еще раз, теперь уже от функции
тем,
что имеет меньшую дисперсию. Следовательно, можно вычислить автокорреляционную
функцию еще раз, теперь уже от функции ![]() . В
результате получим функцию
. В
результате получим функцию ![]() , которая содержит все
частоты исходной функции
, которая содержит все
частоты исходной функции ![]() , но имеет более
высокое отношение с/ш. Определим увеличение отношения с/ш для второй
автокорреляционной функции
, но имеет более
высокое отношение с/ш. Определим увеличение отношения с/ш для второй
автокорреляционной функции ![]() . С учетом обозначений
(5), соотношение (4) описывающее новое отношение с/ш, вычисленное в
соответствии с методикой, изложенной в [4], примет вид
. С учетом обозначений
(5), соотношение (4) описывающее новое отношение с/ш, вычисленное в
соответствии с методикой, изложенной в [4], примет вид
![]() .
.
Увеличение отношения с/ш по мощности будет равно
![]()
при сравнении функций ![]() и
и ![]() . Если
сравнивать отношение с/ш
. Если
сравнивать отношение с/ш ![]() функции
функции ![]() и отношение с/ш
и отношение с/ш ![]() исходной
функции x(t), то
увеличение отношения с/ш по мощности будет равно
исходной
функции x(t), то
увеличение отношения с/ш по мощности будет равно
![]()
Если процедуру последовательного
переобозначения и вычисления автокорреляционной функции осуществлять N раз, то отношение с/ш возрастет
соответственно в ![]() раз по мощности
раз по мощности
 , (6)
, (6)
где R0 º Re , RN – отношение с/ш, вычисленное для автокорреляционной функции, имеющей номер N в ряду последовательно вычисленных автокорреляционных функций, а отношение с/ш для итерации с номером N
![]() . (7)
. (7)
На рисунке 1 представлена зависимость отношения с/ш (RN) от количества процедур вычисления автокорреляционных функций N для произвольно выбранных исходных отношений с/ш (Re), Т, В. Численные эксперименты по определению зависимости RN от количества процедур, выполненные в среде LabVIEW и выражение (7) дают практически одинаковый результат (коэффициент вариации составляет величину 0,01).
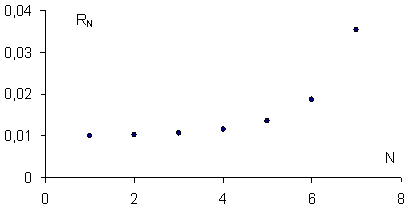
Рис. 1. Зависимость отношения с/ш RN от количества процедур вычисления автокорреляционных функций N.
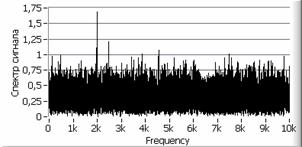
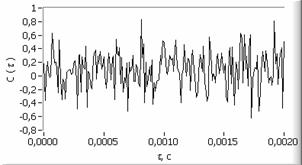
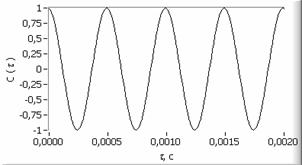
На рисунке 2а представлен фрагмент
исходного сигнала вида (1) с отношением сигнал/шум ![]() , нормированная
автокорреляционная функция сигнала (2б), спектр сигнала (2в) и
спектр автокорреляционной функции (2г).
, нормированная
автокорреляционная функция сигнала (2б), спектр сигнала (2в) и
спектр автокорреляционной функции (2г).


а б

в г
д е
ж з
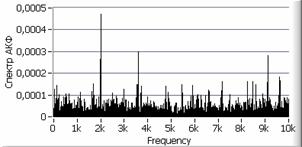
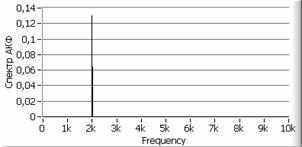
Рис. 2. а – исходный сигнал с
отношением ![]() ,
,
б – автокорреляционная функция сигнала, в – спектр сигнала, г – спектр автокорреляционной функции сигнала, д, е – вторая и пятая автокорреляционная функция, ж, з – их спектры.
Численно моделированный в среде LabVIEW
сигнал содержал 105 дискретных значений, ![]() ,
длительность – 1с. Как видно из рисунка, при таком низком отношении с/ш
обнаружить детерминированную компоненту сигнала s(t) в смеси с шумом по автокорреляционной
функции практически невозможно. Спектры второй (рисунок 2ж) и пятой
(рисунок 2з) автокорреляционных функций содержат указанную гармонику,
причем наблюдается рост отношения с/ш в каждой последующей автокорреляционной
функции.
,
длительность – 1с. Как видно из рисунка, при таком низком отношении с/ш
обнаружить детерминированную компоненту сигнала s(t) в смеси с шумом по автокорреляционной
функции практически невозможно. Спектры второй (рисунок 2ж) и пятой
(рисунок 2з) автокорреляционных функций содержат указанную гармонику,
причем наблюдается рост отношения с/ш в каждой последующей автокорреляционной
функции.
Рассмотрим другой случай, когда исходный сигнал x(t) представляет собой аддитивную смесь периодического, но не гармонического детерминированного сигнала s(t) и шума n(t), являющегося стационарным процессом второго порядка:
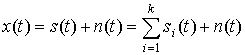 ,
,
где k – количество гармоник сигнала s(t).
Оценка автокорреляционной функции, как и прежде, имеет вид
![]() ,
,
здесь
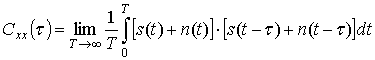 ,
,
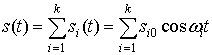
Сделаем ее оценку ![]() :
:
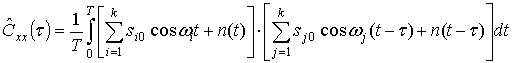 . (8)
. (8)
Выражение (8) содержит слагаемые
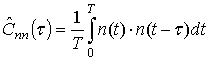 ,
,

а б
в г

д е
ж з
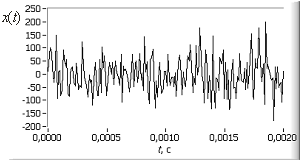
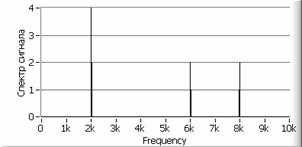
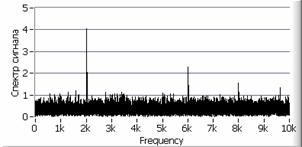
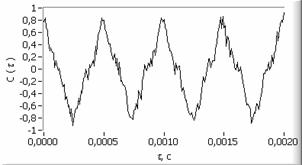
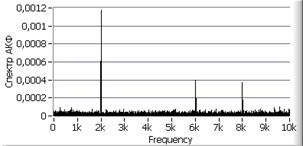
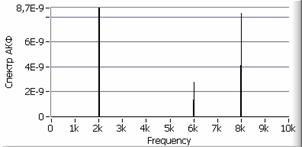
Рис. 3. а – исходный сигнал с
отношением ![]() ,
,
б – автокорреляционная функция сигнала, в – спектр сигнала, г – спектр автокорреляционной функции сигнала, д, е – вторая и пятая автокорреляционная функция, ж, з – их спектры.
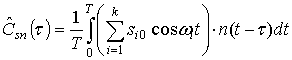 ,
,
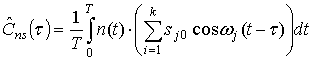 ,
,
которые стремятся с нулю, с ростом Т и
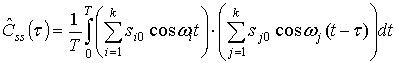 . (9)
. (9)
При ![]() (
(![]() ), слагаемые в (9) стремятся к нулю, а при
), слагаемые в (9) стремятся к нулю, а при
![]() (
(![]() ,
,![]() )
) 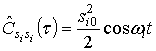 . Это
означает, что спектры всех вычисляемых автокорреляционных функций от
периодических негармонических сигналов содержат только гармоники сигнала
. Это
означает, что спектры всех вычисляемых автокорреляционных функций от
периодических негармонических сигналов содержат только гармоники сигнала ![]() .
.
На рисунке 3 проиллюстрированы результаты
использования предложенного метода полученные с использованием LabVIEW. Сигнал
![]() представлял собой суперпозицию трех
гармоник с частотами 2кГц, 6кГц, 8кГц. Отношение сигнал/шум модельного сигнала,
для гармоники 2кГц
представлял собой суперпозицию трех
гармоник с частотами 2кГц, 6кГц, 8кГц. Отношение сигнал/шум модельного сигнала,
для гармоники 2кГц ![]() . Из рисунка видно, что с
увеличением количества вычисляемых автокорреляционных функций отношение
сигнал/шум увеличивается. На рисунке 3е (пятая автокорреляционная
функция) визуально можно обнаружить только низшую гармонику сигнала, однако
спектр автокорреляционной функции (рисунок 3з) позволяет надежно
обнаруживать все гармоники исходного сигнала
. Из рисунка видно, что с
увеличением количества вычисляемых автокорреляционных функций отношение
сигнал/шум увеличивается. На рисунке 3е (пятая автокорреляционная
функция) визуально можно обнаружить только низшую гармонику сигнала, однако
спектр автокорреляционной функции (рисунок 3з) позволяет надежно
обнаруживать все гармоники исходного сигнала ![]() .
.
Таким образом, показана возможность повышения отношения сигнал/шум слабых гармонических и негармонических периодических сигналов в случае, если для исследования предоставлена только одна реализация сигнала и не существует возможности увеличить длительность сигнала каким-либо образом.
Литература
1. Ван Трис Г. Теория обнаружения, оценок и модуляции. / Пер.с англ. - М., Советское радио, 1972. - Т.1.
2. Макс Ж. Методы и техника обработки сигналов при физических измерениях. – М.: Мир, 1983 – Т.1,2.
3. С.Д. Бураков, А.П. Годлевский, С.А. Останин Определение микрофизических параметров аэрозоля приемопередатчиком на основе твердотельного лазера // Оптика атмосферы.– 1989.– №2.– С. 206-210