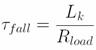Динамика резистивного состояния в узких сверхпроводящих полосках и предельное быстродействие однофотонных сверхпроводниковых детекторов

ДИНАМИКА РЕЗИСТИВНОГО СОСТОЯНИЯ В УЗКИХ СВЕРХПРОВОДЯЩИХ ПОЛОСКАХ И ПРЕДЕЛЬНОЕ БЫСТРОДЕЙСТВИЕ СВЕРХПРОВОДНИКОВЫХ ОДНОФОТОННЫХ ДЕТЕКТОРОВ

А. В. Семенов, А. А. Корнеев, О. В. Окунев, А. В. Антипов
Московский педагогический государственный университет

Получена 14 ноября 2011 г.

Аннотация. Проведено моделирование динамики резистивного состояния, возникающего в смещённой током узкой тонкоплёночной полоске сверхпроводника после поглощения фотона. На этой основе оценено предельное быстродействие сверхпроводникового однофотонного детектора.

Ключевые слова: тонкие сверхпроводящие плёнки, резистивное состояние, сверхпроводниковый однофотонный детектор.

Abstract. We model a dynamics of the resistive state created in narrow current-biased thin-film superconducting strip after absorption of a photon. On basis of this we estimate the ultimate of superconducting single-photon detector.

Keywords: superconducting thin films, resistive state, superconducting single-photon detector.

Последнее десятилетие отмечено бурным развитием квантовых технологий передачи информации [1]. Ключевыми элементами этих технологий являются однофотонные источники, оптико-волоконные линии с малыми потерями и однофотонные детекторы. При этом чрезвычайно привлекательным является использование телекоммуникационных длин волн (1.3 и 1.55 мкм), для которых существуют волокна с наименьшим уровнем потерь (0.2 дБ/км на длине волны 1.55 мкм) и развитая инфраструктура. Среди однофотонных детекторов, работающих в указанном диапазоне, одним из наиболее перспективных сегодня является сверхпроводниковый однофотонный детектор (Superconducting Single-Photon Detector, SSPD), сочетающий такие достоинства, как высокая скорость счёта, низкий уровень ложных срабатываний и простота управляющий электроники [2].

SSPD представляет собой узкую полоску из сверхпроводника (NbN), по которой пропускается ток, близкий к критическому току разрушения сверхпроводящего состояния. При поглощении фотона образуется область с подавленной сверхпроводимостью и ненулевым сопротивлением, что приводит к быстрому уменьшению тока в полоске и регистрации импульса напряжения. Импульс отклика сверхпроводникового однофотонного детектора состоит из двух неравных фаз: резкого переднего фронта и пологого заднего, причём длительность заднего фронта может на два и более порядка превосходить длительность переднего и для стандартных SSPD (меандр длиной 500 мкм) достигает 10 нс [3]. Этой величиной ограничивается временное разрешение детектора. Соответствующая максимальная скорость счёта составляет 600 МГц, что хотя и является одним из лучших показателей для детекторов в ближнем ИК-диапазоне, однако далеко от потолка, определяемого другими элементами квантовой коммуникационной линии. Поэтому исследование физических причин, определяющих длительность отклика SSPD, и способов увеличения быстродействия детектора, весьма актуально.

Как было показано в [3], задний фронт импульса напряжения хорошо описывается моделью релаксации LR-цепочки, V(t)~exp(-t/τ_fall), где

(1)

В качестве сопротивления выступает входной импеданс коаксиальной линии, которой осуществляется съём сигнала с детектора (R_load=50 Ом), а параметр L_k был интерпретирован как кинетическая индуктивность сверхпроводящей полоски детектора. Величина кинетической индуктивности плёнки на квадрат, извлечённая из времени спада заднего фронта и геометрических параметров образцов, оказывается равной приблизительно 100 пГн, что хорошо согласуется с теоретическим значением, даваемым формулой микроскопической теории L_sq_,_k=ћR_sq/πΔ (R_sq – сопротивление квадрата плёнки в нормальном состоянии, ).

Тем самым “длинное” время спада не имеет отношения к механизму срабатывания детектора и является “схемным ограничением”. Для преодоления этого ограничения была разработана конфигурация SSPD в виде N параллельных секций [4], для которой кинетическая индуктивность детектора при той же суммарной чувствительной площади в N² раз меньше, чем для стандартной конфигурации.

Измерения, проведённые в работе [4], действительно продемонстрировали соответствующее уменьшениe времени спада. На рис. 1 (a) представлены импульсы напряжения, возникающие после поглощения фотона в структурах с разным числом параллельных секций 5 и 12. Видно резкое уменьшение длительности импульса с ростом числа секций. Из аппроксимации “хвоста” импульсов релаксационной экспонентой извлекалось соответствующее время спада τ_fall. Для N=12 время спада достигает величины 120 пс. Полученная в эксперименте зависимость τ_fall от числа секций (число секций изменялось от 1 до 12) представлена на рис. 1(b). На том же рисунке построена следующая из формулы (1) зависимость τ_fall~N⁻² (сплошная линия).

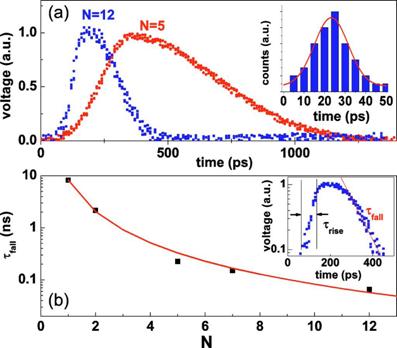
Рис.1. Временные характеристики отклика SSPD, состоящих из параллельно включённых секций. (a) Импульсы напряжения с детекторов, состоящих из 5 и 12 секций. Вставка - джиттер для 12-секционого детектора. (b) Характеристическое время спада τ_fall в зависимости от числа параллельных секций N. Сплошная кривая - зависимость τ_fall~N⁻². Вставка: импульс напряжения с 12-секционного детектора, построенный в полулогарифмическом масштабе.

Полученные в измерениях данные свидетельствуют в пользу того, что для достаточно коротких импульсов кинетическая индуктивность перестаёт быть единственным параметром, определяющим их длительность, и существенной становится собственная динамика резистивного состояния.

Простейшей моделью, позволяющей описать динамику резистивного состояния, является электротермическая модель, подобная используемой для описания явлений тепловой бистабильности в сверхпроводниках, смещённых током (электротепловые домены, горячие пятна). Состояние электронной подсистемы полоски описывается электронной температурой T_e, зависящей от координаты вдоль полоски x. Поглощение фотона моделируется затравочным сопротивлением на длине полоски порядка длины термализации L_th или длины когерентности ξ, смотря по тому, какая из них больше (для плёнок NbN ξ≈7.5 нм [5]). Наличие сопротивления приводит к диссипации на этом участке энергии транспортного тока и к нагреву электронной подсистемы. Это, в свою очередь, влечёт уменьшение локального значения плотности сверхтока, увеличение диссипации энергии и усиление нагрева. Выделяемое в нагретом участке тепло распространяется в соседние области (и, кроме того, в подложку), их температура также повышается, что означает разрастание нагретого участка. Дальнейшая эволюция резистивного состояния зависит от отклика транспортного тока на появляющееся сопротивление, и, тем самым, от «схемных параметров». Для масштабов времён, на которых происходит эволюция резистивного состояния, существенными «схемными параметрами» оказываются кинетическая индуктивность полоски L_k и сопротивление нагрузки (входное сопротивление коаксиальной линии). В случае, если ток фиксирован, резистивная область будет неограниченно разрастаться. Если ток достаточно быстро падает, разогрев резистивной области и электронная температура в ней уменьшаются и резистивная область схлопывается. Ясно, что с уменьшением кинетической индуктивности будет укорачиваться и время реакции тока, и, следовательно, время жизни резистивной области и максимальный размер горячего пятна.

Динамика резистивного состояния в электротермической модели может быть описана следующей системой уравнений:

(2)

(3)

Уравнение (2) представляет собой уравнение теплового баланса, записанное для участка полоски с координатой x. Слева стоит производная по времени от электронной температуры данного участка полоски (C_e – электронная теплоёмкость на единицу длины). В правой части, первый член описывает теплообмен с соседними участками полоски (κ– одномерная теплопроводность плёнки), второй – джоулев нагрев током I (E – напряжённость электрического поля в участке полоски, отличная от нуля при наличии резистивности), третий – уход тепла в фононную подсистему (которая в грубом приближении предполагается находящейся в состоянии теплового равновесия с подложкой) (G – соответствующая одномерная теплопроводность между пленкой и подложкой). Для описания связи между электрическим полем и током используется уравнение резистивной модели:

(4)

где I_s – сверхток, ρ_n – сопротивление полоски на единицу длины в нормальном состоянии.

Уравнение (3) описывает отклик тока на электрическое поле, появляющееся в полоске при наличии сопротивления. I₀ – ток смещения в отсутствие сопротивления в полоске.

В описанной модели электронная подсистема представляется в каждый момент находящейся в состоянии локального равновесия (функция распределения квазичастиц имеет равновесную форму, но с температурой, зависящей от координаты и времени). Условием корректности такого описания является малость времени и длины термализации электронов по сравнению с характерными временами и пространственными масштабами рассматриваемых процессов. В то же время, оценка в рамках этой модели характерного времени джоулева нагрева τ_J=C_e(T_c−T_e)/(I²ρ_n) даёт величину порядка 0.1 пс, что много меньше времени термализации квазичастиц (7 пс [6]). Это означает, что в действительности функция распределения квазичастиц в процессе диссипации энергии тока является неравновесной. Тем не менее, оказывается возможным корректным образом использовать уравнения электротермической модели для описания эволюции резистивного состояния, если учесть запаздывание отклика сверхтока на изменение состояния электронной подсистемы. Именно, поскольку величина критического тока чувствительна лишь к функции распределения квазичастиц в непосредственной окрестности энергетической щели, отклик этой величины на изменение состояния электронной подсистемы наступает лишь к моменту термализации квазичастиц, что можно описать уравнением

(5)

где I_c(T_e) – величина критического тока, соответствующая данной электронной температуре, τ_th – время термализации квазичастиц. При этом τ_th автоматически оказывается и масштабом временных изменений электронной температуры.

a) b)

c) d)

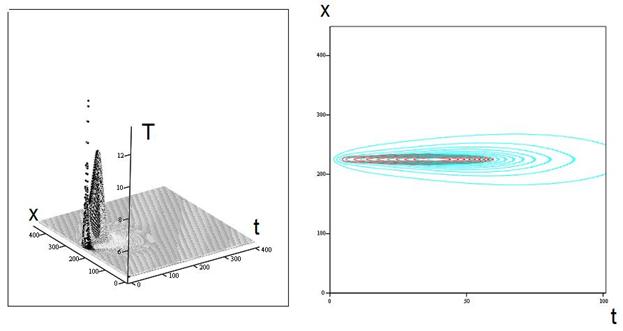
Рис 2. Результаты численных расчётов зависимости электронной температуры (a, c), параметра порядка (голубые изолинии) и электрического поля (красные изолинии) (b, d) от координаты и времени для кинетической индуктивности 500 нГн (a, b) и 5 нГн (c, d). Фотон поглощается в момент времени t=0 в точке с координатой x=225. Единица измерения координаты – 0.5 нм, единица измерения времени – 2 пс.

На рис.2 представлены результаты проведённых нами численных расчётов на основании уравнений (2)-(5). При расчётах были использованы следующие параметры: температура термостата Т0=4.2 К, критическая температура Тс=10 К, эффективная длина когерентности ξ=7.5 нм, постоянная Зоммерфельда γ=240Дж/(K²м³), толщина плёнки 3 нм, ширина полоски 100 нм, сопротивление плёнки на квадрат в нормальном состоянии R_n=700 Ом, рабочий ток I=20 мкА, критический ток при 4.2 К Ic=25 мкА. Численные расчёты показывают, что для индуктивности, соответствующей полоске детектора длиной в 500 мкм (L_k = 500 нГн), время жизни резистивного состояния оказывается равным приблизительно 100 пс, в то время как для кинетической индуктивности в 5 нГн оно сокращается до 50 пс. При этом в первом случае время существования резистивной области приходится в основном на передний фронт импульса, причём успевает сформироваться электротепловой домен. Когда происходит падение тока до величины менее 0.5 I₀, соответствующей абсолютной неустойчивости домена, резистивная область быстро схлопывается и далее происходит релаксационное восстановление тока с постоянной времени 10 нс, даваемой формулой (1). Во втором случае, резистивная область не успевает дорасти до размера, соответствующего электротепловому домену, из-за слишком быстрого падения тока и соответствующего уменьшения джоулева нагрева. Значительная часть времени жизни резистивного состояния приходится на задний фронт импульса, и, тем самым, τ_fall перестаёт определяться только кинетической индуктивностью. Полная длительность импульса, даваемая расчётом, составляет приблизительно 120 пс. Что касается формы переднего фронта, то, как в случае большой, так и в случае малой кинетической индуктивности полученные расчётные зависимости напряжения от времени хорошо согласуются с наблюдаемыми в экспериментах [4].

Таким образом, проведённое моделирование, в согласии с данными эксперимента [4], показывает, что быстродействие SSPD, обусловленное динамикой резистивного состояния в узких полосках NbN, может достигать ≈ 50 ГГц.

Работа выполнена при поддержке ФЦП «Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2007-2012 годы».

Литература

1. R. Hughes and J. Nordholt // Science 333, 1584 (2011).

2. Goltsman G., Minaeva O., Korneev A. et al. //IEEE Trans. Appl. Supercond. 17, 1 (2007).

3. A. Kerman, E. Dauler, W. Keicher et al. // Appl. Phys. Lett. 88, 111 (2006).

4. M. Tarkhov, J. Claudon, J. P. Poizat et al. // Appl. Phys. Lett.-92, 241112 (2008).

5. M. Bell, A. Sergeev, V. Mitin et al. // Phys. Rev. B -.- Vol. 76, 094521 (2007).

6. Semenov A., Gol’tsman G., Korneev A. // Physica C 352, 349 (2001).