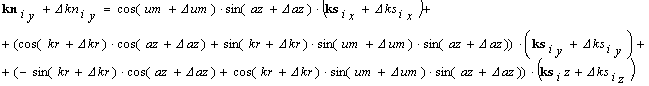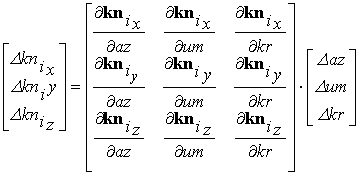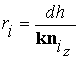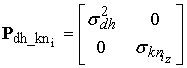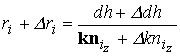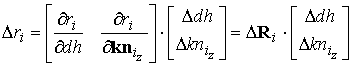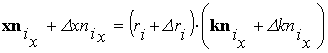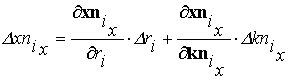УДК 004.93:621.31
Анализ погрешностей определения координат объектов на тепловизионных изображениях при дистанционном обследовании воздушных линий электропередачи *
Г. К. Макаренко 1, А. М. Алешечкин 2
1 ОАО «МРСК Сибири», 2 Сибирский Федеральный Университет
Получена 10 декабря 2012 г.
Аннотация. В представленной работе дано описание разработанного аналитического метода расчета погрешностей определения координат заданных точек тепловизионных изображений. Такие координатно-привязанные тепловизионные изображения могут быть использованы, например, при дистанционной диагностике воздушных линий электропередачи за счет определения мест локальных перегревов, что является признаком предаварийного состояния. В статье предложен алгоритм расчета среднеквадратических погрешностей определения координат заданных точек тепловизионных изображений на основе известных погрешностей измерения первичных влияющих параметров (координаты и угловая ориентация летательного аппарата, и т.д.). Проведено сравнение погрешностей, полученных аналитическим методом, с результатами оценок погрешностей, полученных методом статистического моделирования, подтвердившее правильность полученных результатов. Материал докладывался на 6-й Всероссийской конференции "Радиолокация и радиосвязь" [1].
Ключевые слова: воздушные линии электропередач, тепловизоры, навигация, координаты, погрешности.
Abstract: In the present paper we describe the developed analytical method of calculation errors in determining the coordinates of the given points thermal images. These coordinate attached thermal images can be used, for example, in remote diagnostics of overhead power lines by determining their hot spots, a sign of pre-emergency state. An algorithm calculating a standard error of determining the coordinates of the given points based on thermal images of known errors in the measurement of the primary influencing parameters (coordinates and angular orientation of the aircraft, etc.). A comparison of errors obtained by an analytical method with the results of estimates of the errors produced by the method of statistical modeling, which confirmed the validity of the results. Material reported at the 6th All-Russian Conference "Radars and communications" [1].
Key words: Overhead power line, infra-red chamber, navigation, position, position error.
Введение
В России общая протяженность магистральных воздушных линий (ВЛ) электропередачи составляет более 120 тыс. км [2]. Эффективная эксплуатация ВЛ требует периодической диагностики последних и точного определения координат мест выявленных в ходе диагностики повреждений.
В настоящее время система профилактического обслуживания ВЛ характеризуется низкими оперативностью и точностью выявления координат мест аварийных и предаварийных состояний энергетических объектов.
Повысить эффективность диагностики состояния и определения места повреждения линий электропередач и других объектов электроэнергетики способны летательные аппараты (ЛА), оснащенные средствами тепловизионного обследования [3]. Это позволит выявлять дефекты на ранней стадии их развития, в режиме работы под напряжением, что минимизирует возможность преждевременного выхода оборудования из строя [4].
Авторами статьи в работах [5, 6] предложен комплекс диагностики ВЛ, объединяющий в себе беспилотные ЛА, аппаратуру спутниковых радионавигационных систем (СРНС), и средства получения фото- и тепловизионных изображений. Данный комплекс позволит решать задачи диагностики ВЛ в автоматическом режиме согласно сформированному полетному заданию. Затем полученные фото - и тепловизионные изображения обрабатываются с целью обеспечения их координатной привязки. Разработанный авторами алгоритм определения координат заданных точек тепловизионных и фотоизображений также приведен в источниках [5, 6].
Целью данной работы является оценка погрешностей координатной привязки изображений, получаемых при помощи диагностического комплекса, предложенного в [5, 6].
В настоящей работе решаются следующие задачи:
– разработка алгоритма расчета значений погрешностей координатной привязки полученных фото- и тепловизионных изображений на основе аналитических соотношений, позволяющий определять погрешности координатной привязки заданных точек тепловизионных изображений без необходимости проведения затратного по времени статистического моделирования;
– расчет значений погрешностей по предложенному алгоритму;
– сравнение полученных аналитическим методом значений погрешностей с оценками погрешностей, полученных методом статистического моделирования.
2. Исходные данные
Для
решения поставленной задачи, состоящей в расчете погрешностей требуется знание
исходных значений координат и угловой ориентации беспилотного ЛА, на борту
которого установлена камера тепловизора: широты 
;
долготы 
; высоты 
; азимута 
; угла места 
; крена
, а также углов обзора камеры тепловизора:
; 
и
высоты полета ЛА над землей 
,
определяемой при помощи барометрического или радиовысотомера.
Кроме исходных данных, требуемых для решения задачи определения координат заданной точки изображения необходимы значения погрешностей измерения вышеперечисленных исходных данных, в частности:
–
– среднеквадратическое отклонение (СКО)
погрешности определения высоты ЛА над землей при помощи высотомера;
–
, 
– СКО
погрешности определения географических координат ЛА при помощи приемника
сигналов спутниковой радионавигационной системы (СРНС);
–
– СКО погрешности определения высоты ЛА
при помощи аппаратуры потребителей СРНС;
–
, 
, 
– среднеквадратические погрешности
определения азимута, угла места и крена ЛА.
При расчете погрешностей определения координат точек снимка, погрешности задания начальных значений азимута, угла места и крена ЛА считаются некоррелированными между собой. В этом случае корреляционная матрица погрешностей задания априорной ориентации ЛА определяется в виде:
|
|
(1) |
В качестве заданных точек тепловизионных изображений принимают центр, левый нижний, левый верхний, правый верхний и правый нижний углы тепловизионного изображения [5, 6]. Данным точкам приписывают индексы i = 0, 1, 2, 3 и 4 соответственно. Следует отметить, что координатная привязка указанных точек тепловизионного изображения обеспечивает возможность однозначного определения координат любой другой заданной точки, находящейся на данном тепловизионном изображении или фотоснимке.
3. Алгоритм расчета погрешностей
Задача расчета погрешностей содержит следующие основные этапы.
Согласно приведенному в [5, 6] алгоритму координатной привязки тепловизионных и оптических изображений, получаемых с борта ЛА, на основе заданных значений направляющих косинусов на точки изображения в связанной с объектом (ЛА) системе координат осуществляется пересчет значений погрешностей параметров пространственной ориентации ЛА в погрешности направляющих косинусов пяти векторов от центра объектива камеры тепловизора до точек 0, 1, 2, 3, 4, в топоцентрической системе координат (ТЦСК). Значения направляющих косинусов в ТЦСК функционально связаны со значениями направляющих косинусов в связанной с ЛА системе координат (СК) и являются результатами косвенных измерений [7]. Прямыми измерениями являются углы пространственной ориентации ЛА.
Уравнения
для расчета направляющих косинусов вектора от центра объектива камеры
тепловизора до i-й точки тепловизионного изображения в ТЦСК (
,
,) имеют вид [6]:
|
|
(2) |
При
наличии погрешностей определения азимута, угла места и крена ЛА 
, 
, 
, которые полагаются малыми по сравнению с
действительными значениями азимута, угла места и крена ,
, 
уравнения
(2)
запишутся в виде:
|
|
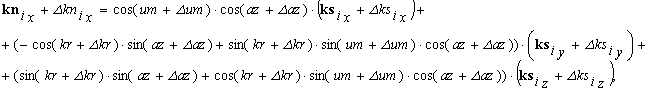
(3) |
Выражения (3) раскладываются в ряд Тейлора. В силу малости погрешностей в сравнении с действительными значениям азимута, угла места и крена в данном ряде могут быть удержаны только линейные члены разложения, компоненты разложения более высоких порядков могут быть отброшены.
Перейдя в выражении (3) к рассмотрению погрешностей измерений, получают выражение для погрешностей определения направляющих косинусов на i-ю точку изображения, которое удобно записать в матричном виде:
|
|
(4) |
Корреляционная матрица погрешностей оценки направляющих косинусов вектора i-й точки снимка в ТЦСК определяется согласно выражению:
|
|
(5) |
где: 
(3´3) -
корреляционная матрица погрешностей определения направляющих косинусов вектора i-й
точки снимка в ТЦСК. На главной диагонали матрицы находятся
дисперсии оценок направляющих косинусов векторов точек снимка в ТЦСК, а вне ее
– корреляционные моменты связи погрешностей; 
-
корреляционная матрица погрешностей определения угловой ориентации, заданная в
соответствии с (1).
Согласно приведенному в [5, 6] алгоритму расчета координат заданных точек изображений по полученным значениям направляющих косинусов в ТЦСК на основе известной высоты полета ЛА над землей определяется расстояние от центра объектива камеры тепловизора до точек тепловизионного изображения в соответствии с формулой:
|
|
(6) |
где i=0, 1, 2, 3, 4 –
номер заданной точки тепловизионного изображения.
Погрешности
измерения высоты полета ЛА над землей 
и определения направляющих
косинусов векторов точек снимка в ТЦСК полагаются также некоррелированными,
поскольку измерения угловой ориентации и высоты полета выполняются разными
устройствами (аппаратура потребителей СРНС и высотомер). Исходя из этого
корреляционная матрица погрешностей задания высоты и z-составляющей
направляющих косинусов вектора i-й точки снимка в ТЦСК
определяется в виде:
|
|
(7) |
При
наличии погрешностей измерения 
, 
выражение (6) принимает
вид:
|
|
(8) |
Для упрощения анализа выражение (8) также раскладывается в ряд Тейлора. В силу малости погрешностей по сравнению с действительными значениями величин в рассмотрении остаются только линейные члены разложения. Погрешности измерений расстояния от i-й точки снимка до центра объектива камеры тепловизора определяются как:
|
|
(9) |
Далее вычисляются значения
частных производных вектора 
, на основе которого
определяется дисперсия определения расстояния от i-й точки снимка до центра
объектива камеры тепловизора:
|
|
(10) |
На следующем этапе алгоритма расчета координат тепловизионных изображений [5, 6] осуществляют определение координат заданной точки в ТЦСК, что выполняется в соответствии с выражениями:
|
|
(11) |
Можно показать, что погрешности задания значений направляющих косинусов векторов точек снимка в ТЦСК по x,y-составляющим и расстояния от камеры до i-й точки являются некоррелированными.
При
наличии погрешностей 
, 
, 
выражение (11) для 
принимает вид:
|
|
(12) |
Разложение (12) в ряд
Тейлора с удержанием линейных членов дает выражения для погрешностей определения
координаты 
:
|
|
(13) |
После вычисления частных производных выражение (13) принимает вид:
|
|
(14) |
Усреднением квадратов левой и правой частей выражения (14) можно определить дисперсию погрешностей определения x-составляющей координат i-й точки снимка в ТЦСК:
|
|
(15) |
где M[.] - означает операцию усреднения (вычисления математического ожидания) величины, заключенной в квадратные скобки.
Аналогичным
образом можно определить дисперсию погрешности определения y
и z - составляющих координат i-й точки
снимка в ТЦСК 
, 
.
Таким образом будут найдены погрешности определения координат i-й точки снимка в ТЦСК, центром которой является центр камеры тепловизора, размещенного на борту беспилотного ЛА.
Аналогичным образом, на основе использования
вышеописанного подхода, могут быть найдены значения СКО погрешности определения
широты 
, долготы 
и
высоты 
для заданной точки тепловизионного
изображения.
4. Результаты моделирования разработанного алгоритма оценки погрешностей
При
моделировании вышеприведенного алгоритма расчета погрешностей осуществлялся расчет
зависимости СКО погрешности 
определения
пространственных координат одной из точек тепловизионного изображения от угла
азимута ЛА, в соответствии с выражением:
|
|
(16) |
, 
, 
– СКО
погрешности определения прямоугольных геоцентрических координат точки (данные
координаты могут быть однозначно получены из широты, долготы и высоты на основе
известных соотношений).
Кроме того, для анализа полученных результатов был произведен расчет погрешностей координатной привязки получаемых изображений на основе использования метода статистического моделирования, исходя из которого на измеряемые исходные параметры накладывались погрешности в виде случайных величин с заданными значениями СКО и нулевыми математическими ожиданиями. Затем проводилось заданное число статистических испытаний, в результате которых рассчитывались статистические оценки СКО определяемых параметров.
В качестве примера рассмотрим расчет погрешностей определения координат точки, принадлежащей левому нижнему углу тепловизионного изображения при следующих исходных данных:
–
координаты и угловая ориентация ЛА, определяемые аппаратурой потребителей СРНС:
широта 
с.ш.; долгота 
в.д.;
высота 
м.; азимут 
; угол
места 
; крен 
0°;
–
углы обзора камеры тепловизора типа TH7102 NEC [8]: 
;
;
–
высота ЛА над землей 
м,
определяемая при помощи барометрического или радиовысотомера;
–
= 10 м – СКО погрешности определения
высоты ЛА над землей при помощи высотомера;
–
= 0,032'', 
=
0,058'' – СКО погрешности определения географических координат ЛА при помощи
приемника спутниковых сигналов (указанные значения и соответствуют СКО погрешности 
=1 м определения координат ЛА в горизонтальной
плоскости);
–
= 10 м – СКО погрешности определения
высоты ЛА при помощи аппаратуры потребителей СРНС;
–
= 10', 
= 20',
= 20' – среднеквадратические погрешности
определения азимута, угла места и крена ЛА;
– z = 100 – число статистических испытаний в каждом заданном значении азимута ЛА.
В
результате моделирования получены зависимости СКО погрешностей определения
направляющих косинусов векторов от центра объектива камеры тепловизора до заданной
точки тепловизионного изображения в ТЦСК от угла азимута ЛА в проекциях на ось x – 
и ось y – 
,
показанные на рис. 1.
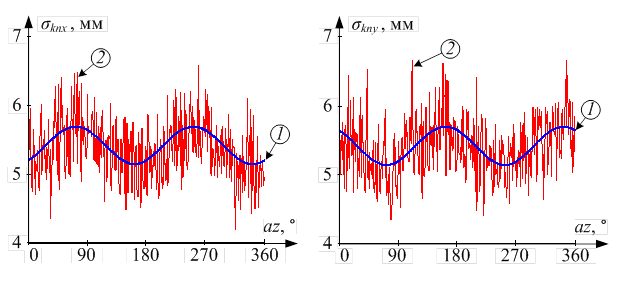
Рис. 1. Кривые
погрешностей определения направляющих косинусов, полеченные:
1) аналитическим
методом; 2) методом статистического моделирования.
Зависимости
СКО погрешностей определения расстояния от центра объектива камеры тепловизора
до заданной точки тепловизионного изображения 
от угла азимута ЛА иллюстрирует рис. 2.
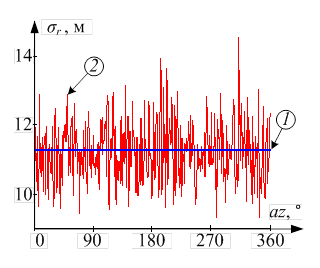
Рис. 2. Зависимости погрешностей определения расстояния, полученные:
1) аналитическим методом; 2) методом статистического моделирования.
Зависимости
СКО погрешностей определения координат x – 
и y –
заданной точки тепловизионного изображения в ТЦСК от
угла азимута ЛА приведены на рис. 3.
Рис. 3. Зависимости погрешностей определения координат, полученные:
1) аналитическим методом; 2) методом статистического моделирования.
Зависимости
СКО погрешностей определения прямоугольных геодезических координат x – 
, y –
и z – 
заданной точки тепловизионного изображения от угла азимута ЛА приведены
на рис. 4.
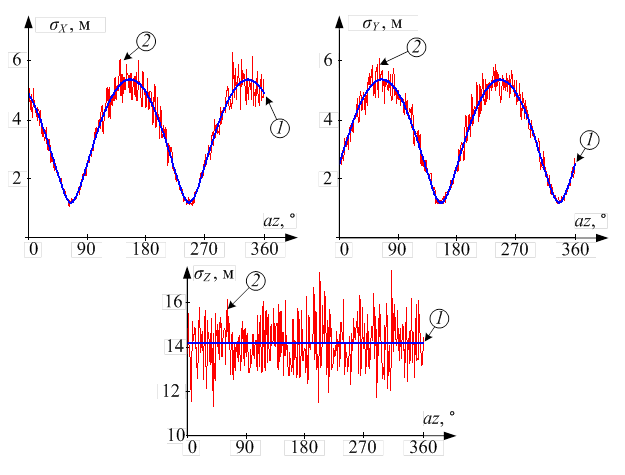
Рис. 4. Зависимости
погрешностей определения прямоугольных геодезических координат, полученные:
1)
аналитическим методом; 2) методом статистического моделирования.
Зависимость
СКО погрешности определения координат объекта в точке принадлежащей левому нижнему
углу тепловизионного изображения от азимута
ЛА в диапазоне 0° – 360° при четырех значениях крена приведена на рис. 5
Рис. 5.
Зависимость СКО погрешности определения координат объекта от углов азимута и
крена ЛА, полученные:
1) аналитическим методом; 2) методом статистического
моделирования.
Приведенные на рис.1–5 зависимости наглядно демонстрируют соответствие результатов статистического и аналитического методов расчета погрешностей координатной привязки получаемых изображений. Значения погрешностей, полученные аналитическим методом, представляют собой математические ожидания оценок полученных методом статистического моделирования. При этом, при увеличении крена ЛА (рис. 5) происходит возрастание погрешности определения координат заданной точки, что объясняется ростом расстояния от камеры тепловизора до точки съемки.
Аналогичные результаты получены для остальных точек тепловизионного изображения.
5. Выводы
Анализ полученных результатов расчета погрешностей координатной привязки получаемых изображений методами статистического и аналитического моделирования, показывает, что методы имеют расхождение менее 1% (число статистических испытаний в методе статистического моделирования составило z=100), что позволяет оценивать погрешности только аналитическим методом по предложенному алгоритму, избегая затратных по времени вычислений, присущих методу статистического моделирования. Кроме того, дополнительным достоинством аналитического метода является возможность учета корреляции между измеряемыми значениями, для чего требуется только изменение вида корреляционных матриц измеряемых параметров (они перестают быть диагональными), при этом алгоритм расчета погрешностей не изменяется.
Предложенный алгоритм может быть использован при определении параметров полета диагностического ЛА для достижения заданной точности определения координат мест повреждений объектов, подлежащих диагностике, а также в оценке точности координатной привязки объектов на полученных тепловизионных изображениях и фотоснимках. Следует отметить, что при оценке погрешностей определения координат объектов в реальных условиях следует учитывать, что разрешающая способность средств тепловизионной– или фотосъемки ограничена, а значит к рассчитанным значениям погрешностей следует дополнительно прибавить погрешность, обусловленную разрешающей способностью фото- или тепловизионной камеры.
Литература
1. Макаренко Г. К. Аналитический метод расчета погрешностей определения координат точек тепловизионных изображений при дистанционном обследовании наземных объектов [Текст] / Г.К. Макаренко, А.М. Алешечкин // материалы VI Всероссийской науч.–тех. конф. «Радиолокация и радиосвязь» (19–22 нояб. 2012, г. Москва) : в 2 т.; Институт Радиотехники и электроники им. В.А. Котельникова РАН. –Москва, 2012. – 401 с. – C. 17 – 20.
2. Сайт Федеральной сетевой компании Единой энергетической системы [электронный ресурс]. URL: http://www.fsk-ees.ru/about.html.
3. Сучкова Г. А. Комплексное обследование и контроль технического состояния элементов ВЛ неразрушающими методами // Энергетик. 2008. №4 С. 20–22.
4. Шалыт Г. М. Определение мест повреждения в электрических сетях. М.: Энергоатомиздат, 1982. 312 с.
7. Винокуров В.И. Электрорадиоизмерения. М.: Высш. шк., 1986. 351 с.
8. Тепловизор Thermo Tracer TH7102 производства NEC [электронный ресурс]. URL: http://www.analyzers.ru/teplovizori/necth7102/.