Погрешности реконструкции параметров токового диполя сердца для неоднородной модели торса человека в виде кругового цилиндра [1]
М. Н. Крамм, Н. О. Стрелков, М. В. Сушок
Национальный исследовательский университет «Московский энергетический институт»
Получена 17 декабря 2012 г.
Аннотация. В данной работе анализируются погрешности реконструкции координат и ориентации дипольного источника потенциалов сердца по электрическим потенциалам, измеренным на поверхности торса человека. Рассматривается влияние выбора модели грудной клетки человека и числа точек съема поверхностных потенциалов на параметры реконструированного токового диполя сердца, включая треки движения диполя и годографы вектора дипольного момента. Полученные годографы также сравниваются с годографами, рассчитанными по методу векторкардиографии Эрнеста Франка. Выводы об эффективности используемых методов делаются на основе найденных погрешностей реконструкции.
Ключевые слова: электрокардиография, векторкардиография, токовый диполь сердца, электрические потенциалы, модель торса человека, неоднородности, обратная задача, реконструкция, треки, годографы.
Abstract. In this study we analyze the errors of reconstruction of heart dipole source parameters (position and orientation) from electric potentials measured on human torso surface. We investigate the effect of selecting human torso model and number of points in which surface potentials are measured on reconstructed dipole parameters (dipole trajectories – tracks and dipole moment vector hodographs). Obtained hodographs are compared with vectorcardiography method, developed by Ernest Frank. Conclusions about effectiveness of the methods are made on base of calculated reconstruction errors.
Keywords: electrocardiography, vectorcardiography, heart current dipole, electric potentials, human torso model, inhomogeneities, inverse problem, reconstruction, track, hodograph.
Основной методикой электрофизиологической диагностики сердца является электрокардиография. Однако электрокардиограммы несут информацию в основном об уровне возбуждения миокарда, не обеспечивая прямого измерения координат и ориентации источников электрической активности сердца. Для повышения информативности диагностических исследований деятельности сердца актуальным является решение обратной задачи электрокардиографии, рассматриваемой, как реконструкция дипольного токового источника (ДТИ) – определение координат и проекций вектора дипольного момента по электрическим потенциалам, регистрируемым в местах размещения поверхностных электродов.
На кафедре ОРТ НИУ «МЭИ» ведется разработка алгоритмов реконструкции характеристик эквивалентных токовых источников по сигналам электродных отведений. Одним из таких алгоритмов является алгоритм, основанный на предположении об однородности и неограниченности проводящей среды, в которой расположен токовый диполь [1]. Позднее был разработан алгоритм [2], который в отличие от созданного ранее учитывает влияние границы между торсом и окружающим воздухом на результаты реконструкции. Решение обратной задачи предполагает в процессе поиска ДТИ использование алгоритма решения прямой задачи, т.е. расчета электрических потенциалов на поверхности грудной клетки, создаваемых токовым диполем. Критерием поиска является минимизация суммы квадратов отклонений измеренных поверхностных потенциалов и потенциалов варьируемого ДТИ [1, 2].
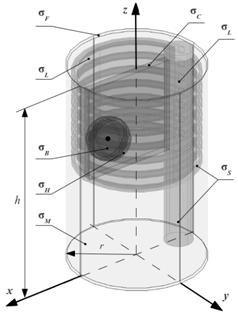
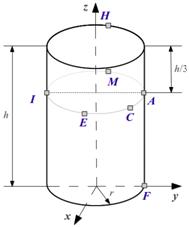
В данной работе, для оценки погрешности реконструкции по алгоритмам [1, 2], в качестве модели грудной клетки (ГК) человека используется электродинамическая модель в форме кругового цилиндра, содержащего внутренние неоднородности (далее по тексту полная неоднородная модель): миокард и полость с кровью, кости (ребра, грудина и позвоночный столб), легкие, скелетные мышцы и слой подкожного жира. Цилиндр окружен непроводящей средой – воздухом. На рис. 1 изображена неоднородная модель грудной клетки человека в форме кругового цилиндра. Радиус цилиндра составляет r = 15.5 см, высота – h = 48 см. Значения проводимостей перечисленных участков внутренней среды ГК выбраны
полость сердца с кровью радиусом 4.25 см – 
См/м, миокард с внешним радиусом
5 см – 
См/м, кости – 
См/м, легкие – 
См/м, полость грудной клетки – 
См/м, скелетные мышцы –
См/м, кожа и подкожный жир – 
См/м. Внутри кругового
неоднородного цилиндра расположен точечный токовый диполь, характеризующийся
координатами положения 
и проекциями вектора дипольного
момента 
.
|
а) |
б) |
|
Рис. 1. Неоднородная модель грудной клетки человека в форме кругового цилиндра: а) в объеме; б) сечение на уровне экватора сферы сердца (z = 2h / 3). |
|
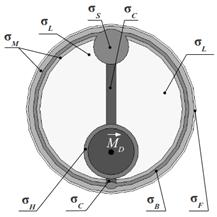
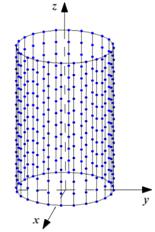
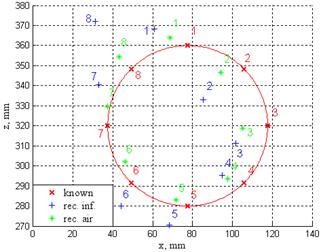
Методические погрешности реконструкции обусловлены как неучетом внутренних неоднородностей (погрешности 1 типа), так и ограниченным количеством и расположением точек съема потенциалов (погрешности 2 типа). Для оценки погрешностей 1 типа использовалась система с достаточно большим числом точек съема потенциалов (312), расположенных в узлах равномерной сетки на боковой поверхности кругового цилиндра. При этом расстояние между горизонтальными круговыми рядами точек – 4 см, шаг по углу между соседними точками, расположенными на одной высоте, – 15° (рис. 2а). Для совместной оценки погрешностей 1 и 2 типа рассматривалась система с 17 точками съема (рис. 2б), расположенными в виде 2 рядов, окружающих область миокарда, с расстоянием между рядами 2w = 8 см [1]. С целью сопоставления результатов с известной методикой векторной электрокардиографии использовалась система отведений Э.Франка (рис. 2б), которая представляет собой ортогональные отведения, отражающие проекции потенциалов сердца на три взаимно перпендикулярные плоскости: фронтальную, горизонтальную и сагиттальную [3].
|
а) |
б) |
в) |
|
Рис. 2. Системы съема
электрических потенциалов: |
||
Для оценки погрешности реконструкции
ДТИ сначала решалась полная прямая задача – при заданных координатах и
ориентации ДТИ, методом конечных элементов (МКЭ) для неоднородной модели
грудной клетки (рис. 1), вычислялись поверхностные потенциалы в точках съема. Токовый диполь задавался координатами
положения 
и проекциями вектора дипольного момента 
. Затем по рассчитанным значениям
поверхностных потенциалов проводилась реконструкция координат и проекций
вектора момента ДТИ алгоритмом [1] и алгоритмом [2], которые не учитывают
внутренних неоднородностей торса. Исследовалось влияние положения и ориентации
вектора дипольного момента на погрешность реконструкции этих параметров.
В первой группе модельных экспериментов ДТИ перемещался для наглядности по окружности с радиусом 4 см, находящейся внутри окружности, ограничивающей полость миокарда с кровью (рис. 1б). При этом линия движения диполя (далее трек) располагался во фронтальной (yz), горизонтальной (xy) и сагиттальной (zx) плоскостях. Вектор дипольного момента был направлен по линии плеч (ось y), по вертикали (ось z) и по направлению от спины к груди (ось x).
Во второй группе модельных экспериментов ДТИ фиксировался в центре миокарда, и конец вектора дипольного момента описывал окружность во фронтальной, горизонтальной и сагиттальной плоскостях. При этом, помимо реконструкции также производится расчет проекций вектора дипольного момента по методу векторкардиографии Э.Франка [3].
Реконструкция параметров токовых
диполей выполнялась согласно стратегии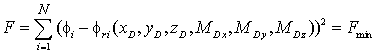 
, в
которой 
–
исходные поверхностные потенциалы, найденные по полной неоднородной модели; 
–
потенциалы ДТИ, реконструированного по алгоритмам [1] или [2], N – число точек съема.
Для оценки погрешностей реконструкции
рассматривались следующие величины: абсолютные погрешности положения диполя: 
, 
, 
, 
, где 
– координаты положения реконструированного диполя; относительные погрешности проекций
момента: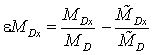 
, 
, 
, 
–
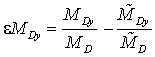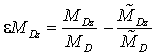характеризуют изменение направления 
; 
, 
, 
, 
–
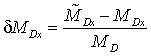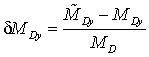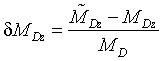характеризуют изменение модуля 
; где 
и 
–
модули векторов моментов исходного и реконструированного диполей; относительные
погрешности поверхностных потенциалов: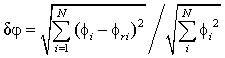 
.
В ходе реконструкции параметров токовых диполей при их движении были получены усредненные погрешности, указанные в таблицах 1-3, где введены сокращения: БС – алгоритм [1], использующий модель безграничной проводящей среды, ВГ – алгоритм [2], учитывающий границу между торсом и окружающим воздухом, т.с. – точки съема потенциалов.
Таблица 1
Средние погрешности при движении диполя в горизонтальной плоскости (ху)
|
Средние погрешности |
x-ориент. |
y-ориент. |
z-ориент. |
||||
|
312 т.с. |
17 т.с. |
312 т.с. |
17 т.с. |
312 т.с. |
17 т.с. |
||
|
|
БС |
1.56 |
9.90 |
1.67 |
2.98 |
6.30 |
3.13 |
|
ВГ |
1.00 |
1.75 |
1.00 |
2.02 |
1.55 |
4.26 |
|
|
|
БС |
0.89 |
7.35 |
0.52 |
0.89 |
3.87 |
2.16 |
|
ВГ |
0.31 |
0.38 |
0.42 |
0.50 |
0.21 |
0.51 |
|
|
|
БС |
0.20 |
0.16 |
0.14 |
0.35 |
0.06 |
0.08 |
|
ВГ |
0.07 |
0.24 |
0.12 |
0.26 |
0.09 |
0.27 |
|
|
|
БС |
8.18 |
7.76 |
7.44 |
9.61 |
17.72 |
8.73 |
|
ВГ |
2.89 |
5.87 |
3.61 |
6.41 |
1.99 |
1.14 |
|
Таблица 2
Средние погрешности при движении диполя во фронтальной плоскости (уz)
|
Средние погрешности |
x-ориент. |
y-ориент. |
z-ориент. |
||||
|
312 т.с. |
17 т.с. |
312 т.с. |
17 т.с. |
312 т.с. |
17 т.с. |
||
|
|
БС |
1.42 |
3.11 |
2.16 |
3.62 |
6.40 |
4.12 |
|
ВГ |
0.92 |
1.66 |
1.02 |
1.97 |
1.68 |
8.46 |
|
|
|
БС |
0.85 |
1.00 |
0.74 |
1.17 |
4.35 |
2.47 |
|
ВГ |
0.30 |
0.36 |
0.47 |
0.48 |
0.32 |
1.02 |
|
|
|
БС |
0.22 |
0.20 |
0.34 |
0.48 |
0.06 |
0.13 |
|
ВГ |
0.06 |
0.20 |
0.20 |
0.25 |
0.11 |
0.63 |
|
|
|
БС |
9.17 |
6.93 |
10.95 |
12.12 |
20.00 |
13.82 |
|
ВГ |
2.87 |
5.59 |
3.63 |
9.30 |
1.98 |
19.88 |
|
Таблица 3
Средние погрешности при движении диполя в сагиттальной плоскости (zx)
|
Средние погрешности |
x-ориент. |
y-ориент. |
z-ориент. |
||||
|
312 т.с. |
17 т.с. |
312 т.с. |
17 т.с. |
312 т.с. |
17 т.с. |
||
|
|
БС |
1.88 |
6.99 |
1.97 |
1.76 |
6.09 |
4.03 |
|
ВГ |
1.00 |
1.96 |
1.17 |
1.17 |
1.30 |
6.90 |
|
|
|
БС |
1.52 |
5.84 |
0.33 |
0.43 |
6.03 |
3.34 |
|
ВГ |
0.21 |
0.32 |
0.46 |
0.45 |
0.28 |
0.78 |
|
|
|
БС |
0.30 |
0.22 |
0.007 |
0.12 |
0.07 |
0.12 |
|
ВГ |
0.11 |
0.24 |
0.006 |
0.10 |
0.11 |
0.39 |
|
|
|
БС |
9.73 |
8.34 |
6.80 |
7.51 |
19.53 |
14.34 |
|
ВГ |
2.99 |
6.33 |
3.15 |
4.81 |
2.33 |
19.76 |
|
Анализируя данные,
представленные в табл. 1-3, можно сделать следующие выводы. Погрешности
реконструкции положения диполя 
, проекции момента 
и ориентации вектора момента 
уменьшаются как при переходе от
алгоритма [1] к алгоритму [2], так и при переходе от системы 312 точек съема
потенциалов к системе с 17 точками съема. За исключением случая
вертикально-ориентированного диполя (z-диполя),
погрешности определения координат ДТИ для алгоритма [2] имеют порядок 1 см при
312 т.с. и 1.5-2 см при 17 т.с.; для алгоритма [1] аналогичные погрешности
примерно в 2 раза хуже. Погрешность определения проекций вектора момента по
алгоритму [2] существенно лучше, чем по алгоритму [1], поскольку учет границы
торса с воздухом означает учет увеличения плотности токов проводимости вблизи
поверхности торса [4]. Увеличение погрешности для z-диполя при 17 т.с. говорит о целесообразности модификации
этой системы съема путем увеличения расстояния между точками съема по
вертикали. Относительная погрешность описания поверхностных потенциалов при
использовании алгоритма [2] за счет неучета внутренних неоднородностей (312
т.с.) находится в пределах 2-3%, дополнительное влияние уменьшения числа точек
съема (17 т.с.) приводит к увеличению 
до 5-10%
В ходе реконструкции параметров ДТИ при вращении вектора дипольного момента в плоскостях декартовой системы координат были получены усредненные погрешности, указанные в табл. 4, также в данной таблице указаны усредненные погрешности проекций дипольного момента для метода Э. Франка.
Таблица 4
Средние погрешности при вращении вектора дипольного момента
|
Средние погрешности |
Горизонтальная плоскость (xy) |
Фронтальная плоскость(yz) |
Сагиттальная плоскость (zx) |
||||
|
312 т.с. |
17 т.с. |
312 т.с. |
17 т.с. |
312 т.с. |
17 т.с. |
||
|
|
БС |
1.41 |
1.88 |
4.8 |
2.34 |
4.5 |
3.04 |
|
ВГ |
0.87 |
1.29 |
1.12 |
2.24 |
1.15 |
3.85 |
|
|
|
БС |
0.23 |
0.27 |
0.45 |
0.37 |
0.41 |
0.32 |
|
ВГ |
0.15 |
0.24 |
0.24 |
0.14 |
0.13 |
0.40 |
|
|
|
БС |
8.89 |
9.83 |
16.83 |
12.32 |
15.38 |
13.64 |
|
ВГ |
3.33 |
6.76 |
3.05 |
14.28 |
1.94 |
16.13 |
|
|
Метод Франка (7 т.с.), |
0.28 |
0.15 |
0.23 |
||||
По данным табл. 4 можно сделать следующие выводы: средние
относительные погрешности проекций вектора дипольного момента 
при реконструкции по алгоритму [1]
находятся в интервале 0.23 – 0.45, применение алгоритма [2] позволяет снизить 
до 0.13 – 0.24 (за исключением
отмеченного выше случая z-диполя при 17 точках съема);
при расчете методом Франка 
находится в интервале
0.15 – 0.28. Таким образом, полученные результаты реконструкции ориентации ДТИ
согласуются с данными, получаемыми по методике Франка.
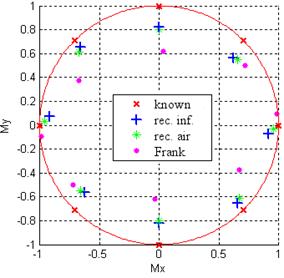
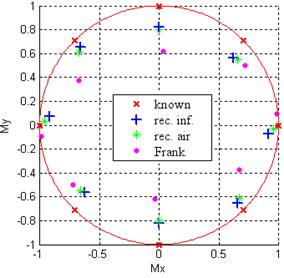
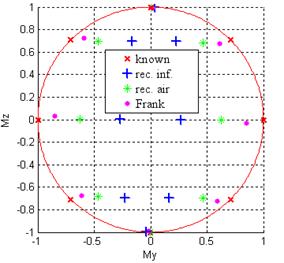
Результаты проведенных экспериментов в наглядном виде могут быть отображены линиями движения ДТИ (треками) и линиями движения конца вектора дипольного момента (годографами). В качестве примера на рис. 3 представлены точки треков движения x-диполя в горизонтальной плоскости, а на рис. 4 – точки нормированных годографов вектора дипольного момента при его вращении также в горизонтальной плоскости для разного числа точек съема потенциалов.
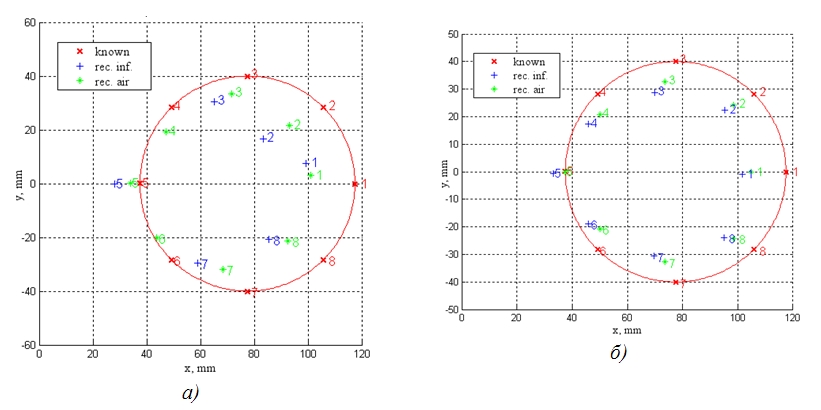
Рис. 3. Треки движения x-ориентированного диполя в горизонтальной плоскости: а) 17 т.с., б) 312 т.с.
Здесь символами “´” показано движение исходного модельного ДТИ, символами “+” результаты реконструкции по алгоритму [1], “*” – по алгоритму [2], “·” – по методике Э.Франка (рис. 2в).
|
а) |
б) |
|
Рис. 4. Нормированные годографы вектора дипольного момента при его вращении в горизонтальной плоскости: а) 17 т.с., б) 312 т.с. |
|
По рис. 3 и 4 можно заключить, что использование большего числа точек съема потенциалов уменьшает погрешности по алгоритму ВГ примерно в два раза, по ВГ годограф для 312 т.с. получается лучше, чем у Э.Франка. Поскольку погрешности определения параметров диполя для 312 т.с. оказываются наименьшими, приведем результаты для других плоскостей именно для такого числа точек съема потенциалов.
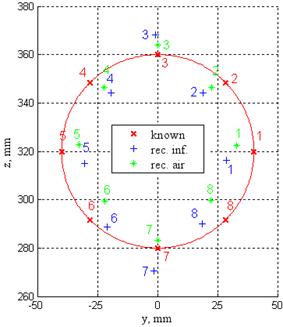
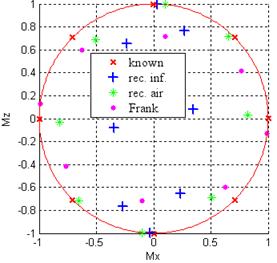
На рис. 5 представлены результаты для фронтальной плоскости (yz) при 312 т.с.
|
а) |
б) |
|
Рис. 5. Трек и годограф
во фронтальной плоскости (yz) для 312 т.с.: |
|
Для трека (рис. 5а) во фронтальной плоскости погрешности с учетом воздушной границы в 1.5 раза меньше, чем для БС. Лучший годограф (рис. 5б) в данной плоскости дает метод Франка, далее идет ВГ.
На рис. 6 представлены результаты для сагиттальной плоскости (zx) при 312 т.с.
Для трека (рис. 6а) в сагиттальной плоскости погрешности по ВГ примерно в два раза меньше, чем для БС. Лучший годограф (рис. 6б) в данной плоскости дает ВГ, оказываясь по погрешности лучше метода Франка в 1.8 раза. Представленные графики визуально подтверждают выводы, сделанные по данным таблиц.
|
а) |
б) |
|
Рис. 6. Трек и годограф
в сагиттальной плоскости (zx) для 312 т.с.: |
|
Таким образом, на основании полученных результатов, можно сделать вывод об уменьшении погрешности реконструкции координат и ориентации токового источника потенциалов в неоднородной модели торса человека при учете границы раздела торса с окружающим воздухом. При этом ошибки реконструкции ориентации ДТИ для алгоритма [2] сопоставимы с результатами, полученными по методу векторкардиографии Э. Франка. Материал настоящей работы докладывался 20 ноября 2012 года на 6-й Всероссийской конференции "Радиолокация и радиосвязь", проходившей в ИРЭ им. В.А. Котельникова РАН [5].
1. Лебедев В.В., Крамм М.Н., Жихарева Г.В., Иванов Г.Г., Попов Ю.Б. Система электродных отведений для измерения координат источников в области миокарда. // Медицинская техника. – 2006. – № 4. С. 7-9.
2. Стрелков Н.О., Винокуров Д.С., Крамм М.Н. Методика реконструкции параметров токового диполя сердца на модели торса человека в виде кругового цилиндра. // Медико-экологические информационные технологии – 2011: сборник материалов XIV МНТК / редкол.: Н.А. Кореневский [и др.]; Юго-Зап. гос. ун-т. – Курск, 2011. – 315 с.
3. Frank E. An accurate, clinically practical system for spatial vectorcardiography. // Circulation. 1956. Vol. 13 (May). P. 737.
4. Стрелков Н.О., Крамм М.Н., Жихарева Г.В. Неоднородная электродинамическая модель грудной клетки человека в форме эллиптического цилиндра // Журнал радиоэлектроники. – 2011. – № 7. – [Электронный ресурс]. – URL http://jre.cplire.ru/jre/jul11/4/text.html (дата обращения 13 октября 2012 г.).
5. Крамм М.Н., Стрелков Н.О., Сушок М.В. Анализ погрешностей реконструкции дипольного источника потенциалов сердца для неоднородной цилиндрической модели торса человека. // Радиолокация и радиосвязь. Сборник докладов VI Всероссийской научно-технической конференции в 2-х т. – М.: JRE - ИРЭ им. В.А. Котельникова РАН, 2012. Т. 2 – 401 с. С. 301-305.