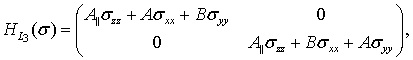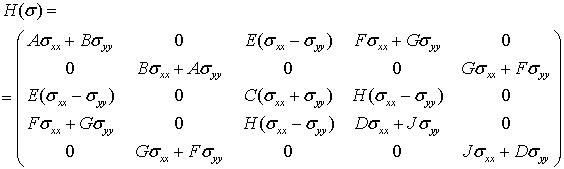УДК 538.9
Исследование Ni в ZnO методом одноосного сжатия
Ю. С. Кутьин 1, Э. В. Лавров 2
1 Казанский федеральный университет
2 Институт радиотехники и электроники им. В.А. Котельникова РАН
Получена 17 декабря 2012
Аннотация. Исследуется влияние одноосного сжатия
на электронные переходы ![]() иона Ni2+ (d8) в ZnO. Показано,
что расщепление и поляризационные свойства линий ИК поглощения согласуются с
тригональной симметрией и спин-орбитальным расщеплением, установленными в предшествующих
исследованиях.
иона Ni2+ (d8) в ZnO. Показано,
что расщепление и поляризационные свойства линий ИК поглощения согласуются с
тригональной симметрией и спин-орбитальным расщеплением, установленными в предшествующих
исследованиях.
Ключевые слова: оксид цинка, никель, ИК поглощение, электронные переходы.
Abstract:
The influence
of the uniaxial compression on the electron transitions ![]() of Ni2+ (d8)
ion into ZnO is investigated. It has been shown that splitting and polarized
properties of the IR absorption lines are adjusted with the trigonal symmetry
and spin-orbital splitting revealed in the previous investigations.
of Ni2+ (d8)
ion into ZnO is investigated. It has been shown that splitting and polarized
properties of the IR absorption lines are adjusted with the trigonal symmetry
and spin-orbital splitting revealed in the previous investigations.
Key words: zinc oxide, nickel, IR absorption, electron transitions.
1. Введение
ZnO – прямозонный полупроводник с шириной запрещенной зоны 3.3 эВ при комнатной температуре – привлекает большое внимание в последние годы благодаря большому количеству потенциальных приложений, таких как материал для создания синих и ультрафиолетовых светоизлучающих диодов, устойчивый к радиации материал для космических приложений, прозрачный проводящий оксид, и т.д. [1]. Из-за теоретически предсказанной высокой температуры Кюри существует также большой интерес к созданию на основе допированного переходными металлами (Co, Mn, Fe, Ni) ZnO разбавленных магнитных полупроводников [2-6].
Никель – распространенная примесь в ZnO, вносимая в материал во время роста кристалла. Никель
приводит к появлению ряда линий в спектрах фотолюминесценции (ФЛ) и ИК
поглощения оксида цинка. В частности, переходы ![]() иона Ni3+ (d7) возникают в спектрах ФЛ на частотах 6090.5 и 6096.2
см-1 [7]. Переходы
иона Ni3+ (d7) возникают в спектрах ФЛ на частотах 6090.5 и 6096.2
см-1 [7]. Переходы ![]() иона Ni2+ (d8) наблюдаются в ИК поглощении на 4216, 4240, и 4247 см-1
[7,8]. Линия на 8340 см-1 приписывается переходу
иона Ni2+ (d8) наблюдаются в ИК поглощении на 4216, 4240, и 4247 см-1
[7,8]. Линия на 8340 см-1 приписывается переходу ![]() [8]. Недавно было продемонстрировано, что
данный спектр имеет структуру, соответствующую основным изотопам никеля 58Ni, 60Ni и 62Ni, что подтвердило микроскопическую
природу данного дефекта [9].
[8]. Недавно было продемонстрировано, что
данный спектр имеет структуру, соответствующую основным изотопам никеля 58Ni, 60Ni и 62Ni, что подтвердило микроскопическую
природу данного дефекта [9].
Пьезоспектроскопия позволяет определить симметрию дефекта и получить величины скоростей сдвига линий под действием давления, в том числе скорость гидростатического сдвига [10-12]. Методом пьезоспектроскопии недавно исследовалось множество дефектов в ZnO, связанных с водородом и медью [13-15].
В данной работе мы приводим результаты исследования Ni методом одноосного сжатия,
выполненного на переходах ![]() на 4216, 4240, и 4247 см-1.
на 4216, 4240, и 4247 см-1.
2. Описание эксперимента
Образцы ZnO, использованные в экспериментах по
одноосному сжатию –субстраты n-типа,
выращенные гидротермальным способом и поставляемые компанией CrysTec GmbH. Размеры номинально нелегированных образцов,
содержащих примесь Ni, составляли
порядка ![]() мм3. Одноосное сжатие производилось
вдоль наиболее длинной стороны образца, которая вырезалась вдоль оси с,
мм3. Одноосное сжатие производилось
вдоль наиболее длинной стороны образца, которая вырезалась вдоль оси с, ![]() и
и ![]() . Намеренное легирование никелем производилось
на образцах ZnO, выращенных из газовой фазы в Институте
прикладной физики Университета Эрлангена (Германия) [16].
. Намеренное легирование никелем производилось
на образцах ZnO, выращенных из газовой фазы в Институте
прикладной физики Университета Эрлангена (Германия) [16].
Измерения выполнялись в диапазоне давлений до 0.3 ГПа при 8-10 К на самодельном прессе, установленном в гелиевом криостате с окнами из ZnSe. Давление прикладывалось к образцам пневматическим цилиндром и передавалось толкающим стержнем. Поляризованные спектры были получены с помощью проволочного поляризатора на субстрате из KRS-5.
Спектры ИК поглощения были записаны на фурье-спектрометре Bomem DA3.01. Использовался глобар в качестве источника света, светоделитель из CaF2 и детектор на основе InSb, охлаждаемый жидким азотом. Спектральное разрешение составляло 0.25 см-1.
Фотолюминесценция ZnO измерялась при 4.2 К на образцах, погруженных в жидкий гелий в криостате Oxford. Возбуждение осуществлялось на длине волны 325 нм лазером HeCd с мощностью возбуждения около 2 мВт.
3. Допирование оксида цинка никелем
В литературе встречается множество линий ИК поглощения и фотолюминесценции, приписываемых различным переходным металлам, внедренным в ZnO [7,8,17-19]. Недавно Vlasenko и др. продемонстрировали, что часто наблюдаемые в ZnO узкие линии ФЛ на 6885 см-1, которые традиционно приписывались меди, в действительности принадлежат ванадию, входящему в ZnO в качестве непреднамеренно вносимой примеси [20].
Для подтверждения химической природы дефекта, спектр которого изучался в данной работе, выращенные из газовой фазы образцы ZnO намеренно легировались никелем. Образцы помещались в кварцевую ампулу с кусочком никелевой проволоки размером примерно 2 мм3 (чистота материала 99.99%). Ампула затем заполнялось кислородом (0.5 бара при комнатной температуре), запаивалась и помещалась на 40 часов в печку при температуре 950 °С.
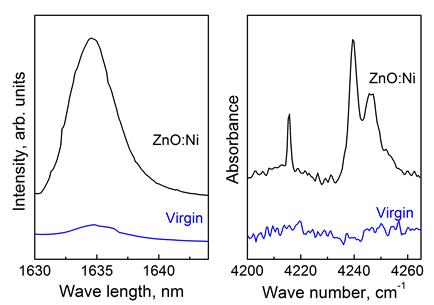
Рис. 1. Фрагменты спектров ФЛ (слева) и ИК поглощения
(справа) образца ZnO, выращенного из газовой фазы. Спектры записаны при
температуре около 10 К до и после диффузии Ni из газовой фазы при 950 °С в течение 40 часов. Спектр
ФЛ соответствует переходу ![]() иона Ni3+, а линии ИК поглощения – переходу
иона Ni3+, а линии ИК поглощения – переходу ![]() иона Ni2+ (для удобства спектры сдвинуты по вертикали).
иона Ni2+ (для удобства спектры сдвинуты по вертикали).
На рис. 1 показаны результаты экспериментов по диффузии Ni. Нижние спектры были записаны до легирования. В данных образцах отсутствуют линии ИК поглощения и ФЛ, приписываемые Ni2+ и Ni3+. Два верхних спектра были сняты непосредственно после обработки образцов. На спектре ФЛ появилась линия на 1640 нм, приписываемая иону Ni3+, а также на спектре ИК поглощения появились три линии на частоте около 4240 см-1, принадлежащие иону Ni2+ [7].
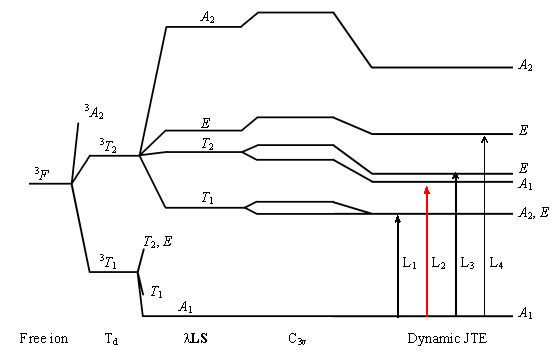
4. Диаграмма энергетических уровней
Замещение цинка никелем не приводит к существенным искажениям решетки ZnO, поскольку ионы Ni2+ и Zn2+ имеет близкие по значению ионные радиусы [21]. Все электронные состояния никеля, замещающего цинк, должны преобразовываться по неприводимым представлениям А1, А2 или Е точечной группы C3v. На диаграмме энергетических уровней Ni2+, приведенной на рис. 2, в порядке уменьшения величины рассматриваются возмущения, действующие на состояние 3F свободного иона. Для ионов переходных металлов кристаллическое поле обычно велико по сравнению со спин-орбитальным взаимодействием [22]. Таким образом, на диаграмме слева направо учтено влияние тетраэдрического кристаллического поля, спин-орбитального взаимодействия и тригонального поля решётки типа вюрцита на основное состояние иона d8.
Рис. 2. Диаграмма энергетических уровней иона Ni2+ в ZnO. Красная и черные стрелки обозначают электрические
дипольные переходы, разрешенные для поляризаций E || c и E ^ c,
соответственно.
Kaufmann и др. продемонстрировали, однако, что статическая теория кристаллического поля не способна адекватно описать наблюдаемые спектры Ni2+ в ZnO [23]. Было показано, что удовлетворительно интерпретировать линии ИК поглощения позволяет учет динамического эффекта Яна-Теллера. Сильная связь между электронными орбитальными состояниями Ni и колебательной модой E оксида цинка приводит к уменьшению всех недиагональных матричных элементов электронных операторов. Диаграмма уровней с учетом эффекта Яна-Теллера показана в правой части рис. 2.
Поскольку измерения по ИК поглощению проводились при температуре около
9 К, только основное состояние А1 является заселенным
(см. рис. 2), и следует рассматривать переходы только с этого состояния. Электрический
дипольный переход между двумя состояниями разрешен, если прямые произведения
неприводимых представлений этих двух уровней с неприводимыми представлениями
электрического дипольного момента d содержат неприводимое представление А1.
В точечной группе C3v вектор d преобразуется
по сумме А1 и Е. Отсюда следует, что переходы ![]() запрещены в электрическом дипольном
приближении, в то время как переходы на уровни А1 и Е
разрешены, соответственно, в параллельной (E || c) и перпендикулярной (E ^ c) поляризации.
запрещены в электрическом дипольном
приближении, в то время как переходы на уровни А1 и Е
разрешены, соответственно, в параллельной (E || c) и перпендикулярной (E ^ c) поляризации.
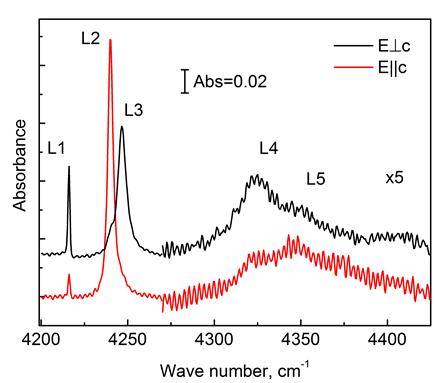
Рис. 3. Поляризованные спектры ИК поглощения иона Ni2+ в ZnO, соответствующие переходам ![]() ,
записанные при 10 К. Для удобства спектры сдвинуты по вертикали.
,
записанные при 10 К. Для удобства спектры сдвинуты по вертикали.
На рис. 3 приведены поляризованные спектры ИК поглощения образца ZnO, выращенного гидротермальным способом и содержащего Ni в качестве неконтролируемой примеси. Видно, что первые три линии (L1, L2 и L3) преимущественно поляризованы, соответственно, перпендикулярно, параллельно, и перпендикулярно оси с, что согласуется с диаграммой энергетических уровней Ni2+ [7, 23].
Отметим, что интенсивность линии L1 в параллельном спектре, вопреки диаграмме никеля, не является исчезающее малой. Для второй и третьей линии поляризационные правила отбора также выполняются нестрого. Похожие эффекты наблюдались также в спектрах поглощения Co2+ (d7) [24] и Cu2+ (d9) [17] в ZnO. Причины такого поведения до конца не ясны. Мы полагаем, что оно объясняется искажениями решетки, приводящими к смешиванию состояний 3F и 3P иона никеля даже в отсутствие внешнего приложенного давления.
Линии L4 и L5 всегда входят в спектры оксида цинка, содержащего Ni, примерно с одинаковыми относительными интенсивностями по сравнению с первыми тремя линиями. Следовательно, эти линии также должны быть приписаны никелю. Отметим, что переход L5 наблюдался прежде, но не был приписан переходам Ni [23]. Линия L4 преимущественно поляризована перпендикулярно, линия L5 – параллельно оси с. Однако степень поляризации в обоих случаях довольно низкая, что не позволяет однозначно интерпретировать данные переходы.
Поскольку переходы L4 и L5 значительно отстоят по энергии от первых трех линий, мы пренебрегаем взаимодействием между двумя этими группами и рассматриваем только переходы L1, L2 и L3.
5. Одноосное сжатие
На рис. 4 показано влияние давления (F), приложенного вдоль с, ![]() и
и ![]() , на переходы L1, L2 и L3, которые принадлежат замещающему цинк Ni. Как и ожидалось, в случае F || c двойное вырождение состояний Е, которым
отвечают переходы L1 и L3, не снимается. Все линии сдвигаются линейно в сторону
больших энергий с близкими скоростями, составляющими 33, 37 и 39 см-1/ГПа для L1, L2 и L3, соответственно.
, на переходы L1, L2 и L3, которые принадлежат замещающему цинк Ni. Как и ожидалось, в случае F || c двойное вырождение состояний Е, которым
отвечают переходы L1 и L3, не снимается. Все линии сдвигаются линейно в сторону
больших энергий с близкими скоростями, составляющими 33, 37 и 39 см-1/ГПа для L1, L2 и L3, соответственно.
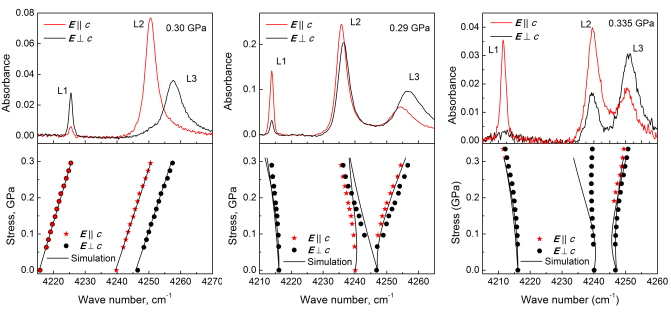
Рис. 4. Поляризованные спектры ИК
поглощения и расщепление линий Ni2+ под
действием одноосного сжатия: ![]() (слева),
(слева), ![]() (посередине)
и
(посередине)
и
![]() (справа). Сплошными линиями показано
расщепление, рассчитанное из выражений (2), (4) и (8). Значения подгоночных
параметров приведены в тексте.
(справа). Сплошными линиями показано
расщепление, рассчитанное из выражений (2), (4) и (8). Значения подгоночных
параметров приведены в тексте.
В случае же, когда давление направлено перпендикулярно оси с, линия L1 смещается нелинейно, и ее суммарная интенсивность растет с давлением. Кроме того, меняются поляризационные свойства линии L1, так, что при давлении s = 0.3 ГПа она поляризована преимущественно параллельно оси с.
Поляризационные свойства линий L2 и L3 также меняются с давлением: запрещенные при нулевом
давлении поляризации становятся существенными при 0.3 ГПа. Кроме того, в
соответствии с ожидаемой картиной расщепления состояний Е в кристаллах с
решеткой типа вюрцита, линия L3 должна вести себя одинаково при
наложении давлении как вдоль ![]() , так и вдоль
, так и вдоль ![]() [25]. Однако результаты измерений, представленные на рис. 4, не
согласуются с данным выводом.
[25]. Однако результаты измерений, представленные на рис. 4, не
согласуются с данным выводом.
Наблюдаемые эффекты можно объяснить, если предположить, что уровни Е, А1 и Е иона Ni2+, которым соответствуют линии поглощения L1, L2 и L3, не являются независимыми. В данном случае энергетические уровни смешиваются под действием давления, что приводит к перераспределению интенсивности и поляризационных свойств между всеми тремя переходами. Необходимо составить Гамильтониан с соответствующими свойствами симметрии, учитывающий взаимодействие между уровнями за счет прикладываемого давления.
Для этого мы выбираем следующие базисные функции: ![]() , и
, и ![]() .
Верхний индекс указывает линию в спектре ИК поглощения, и нижний индекс
обозначает неприводимое представление соответствующего уровня энергии.
.
Верхний индекс указывает линию в спектре ИК поглощения, и нижний индекс
обозначает неприводимое представление соответствующего уровня энергии.
В линейном приближении Гамильтониан системы можно записать как
![]() , (1)
, (1)
где H0 – это Гамильтониан нулевого поля, не зависящий от внешнего давления:
где D = 24 см-1 – разница в энергии между уровнями А1 и Е, соответствующими линиям L2 и L1, а d = 7 см-1 – разница между Е и А1, соответствующими линиям L3 и L2, соответственно (см. рис. 2).
Часть Гамильтониана (1), зависящая от давления, может быть записана как
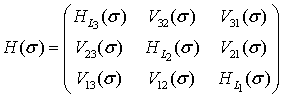 . (3)
. (3)
Матрицы ![]() ,
, ![]() и
и ![]() имеют размерности
имеют размерности ![]() ,
,
![]() и
и ![]() , соответственно.
Они описывают воздействие давления на линии L3, L2, L1 в отсутствие взаимодействия между энергетическими уровнями. Матрицы
Vij описывают вызванное давлением
взаимодействие. Их размерность:
, соответственно.
Они описывают воздействие давления на линии L3, L2, L1 в отсутствие взаимодействия между энергетическими уровнями. Матрицы
Vij описывают вызванное давлением
взаимодействие. Их размерность: ![]() ,
, ![]() и
и ![]() для
для ![]() ,
, ![]() и
и ![]() , соответственно.
, соответственно.
Чтобы получить выражение для Гамильтониана давления в явном виде,
необходимо указать систему координат. Выбираем ![]() и
и ![]() , при этом единственными ненулевыми элементами тензора напряжений sij будут sxx, syy и szz для
, при этом единственными ненулевыми элементами тензора напряжений sij будут sxx, syy и szz для![]() и с,
соответственно.
и с,
соответственно.
Тогда матрицы H(s) могут быть записаны как [25]
![]() (4b)
(4b)
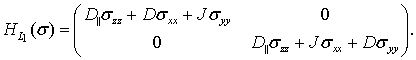 (4c)
(4c)
Как следует из рис. 4, смещение всех трех линий при ![]() линейно с давлением, и подгонка
параметров в данном случае тривиальна: A|| = 33,
C|| = 37
, и D|| = 39 см-1/ГПа.
линейно с давлением, и подгонка
параметров в данном случае тривиальна: A|| = 33,
C|| = 37
, и D|| = 39 см-1/ГПа.
Для подгонки параметров при ![]() необходимо составить
недиагональные матрицы Vij(s). Начнем с разложения возмущения V(s) по неприводимым представлениям точечной группы C3v:
необходимо составить
недиагональные матрицы Vij(s). Начнем с разложения возмущения V(s) по неприводимым представлениям точечной группы C3v:
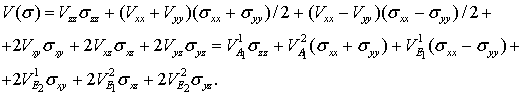 (5)
(5)
Матричные элементы матриц ![]() и
и ![]() вычисляются на функциях, преобразующихся
в соответствии с неприводимыми представлениями Е и А1.
Учитывая также, что
вычисляются на функциях, преобразующихся
в соответствии с неприводимыми представлениями Е и А1.
Учитывая также, что ![]() при
при ![]() , мы
получаем:
, мы
получаем:
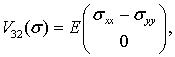 (6a)
(6a)
![]() . (6b)
. (6b)
Матрица ![]() вычисляется на двух наборах
функций, каждый из которых преобразуется по неприводимому представлению Е
и, следовательно, имеет ту же структуру, что и
вычисляется на двух наборах
функций, каждый из которых преобразуется по неприводимому представлению Е
и, следовательно, имеет ту же структуру, что и ![]() и
и ![]() , то есть:
, то есть:
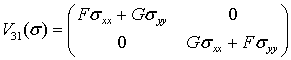 . (7)
. (7)
Собрав вместе все матрицы, мы получаем, что в случае ![]() , то есть при
, то есть при ![]() и
и ![]() , Гамильтониан давления записывается как
, Гамильтониан давления записывается как
Сплошные линии на рис. 4 показывают расщепление линий L1, L2 и L3, полученное из выражений (2), (4) и (8). Найденные
оптимальные значения подгоночных параметров для случая ![]() :
A = -7 ± 5, B = -34 ± 3, C = 16 ± 3,
D = 6 ± 4,
|E| = 27 ± 2,
|F| = 41 ± 5,
|G| = 22 ± 5,
|H| = 11 ± 3,
|J| = 2 ± 3 см-1/ГПа.
Как видно из рис. 4, наша модель удовлетворительно описывает экспериментальные
результаты.
:
A = -7 ± 5, B = -34 ± 3, C = 16 ± 3,
D = 6 ± 4,
|E| = 27 ± 2,
|F| = 41 ± 5,
|G| = 22 ± 5,
|H| = 11 ± 3,
|J| = 2 ± 3 см-1/ГПа.
Как видно из рис. 4, наша модель удовлетворительно описывает экспериментальные
результаты.
6. Обсуждение
Из диаграммы энергетических уровней никеля в ZnO, которую предложили Kaufmann и др. (см. рис. 2) следует, что существует также уровень А2,
расположенный близко к Е, переходу на который соответствует линия L1. Переход ![]() запрещен в
электрическом дипольном приближении и не может наблюдаться в ИК поглощении.
запрещен в
электрическом дипольном приближении и не может наблюдаться в ИК поглощении.
Исследование комплекса Cu-H в ZnO выявило ряд невидимых переходов дефекта, которые
появляются, когда к образцу приложено одноосное сжатие [14]. Данный эффект был
объяснен смешиванием энергетических уровней под действием давления, которое
приводит к переносу интенсивности к комбинационным модам и делает возможным их
наблюдение в спектрах. Подобные результаты ожидались и в случае Ni. Однако в наших измерениях дополнительные
индуцированные давлением линии не наблюдались. Поэтому уровень А2
был исключен из рассмотрения, что позволило сократить размерность Гамильтониана
(8) с ![]() до
до ![]() и,
соответственно, уменьшить число подгоночных параметров.
и,
соответственно, уменьшить число подгоночных параметров.
Еще одно усложнение предложенной модели заключается во влиянии низколежащих уровней никеля (см. рис. 2). В отсутствие давления необходимо учитывать только переходы с основного состояния А1, т.к. измерения проводились при температуре 9 К. Однако возможна ситуация, когда состояния расщепляются и/или сдвигаются под действием давления, и часть компонент подходят близко к основному уровню и также становятся заселенными при 9 К (см., к примеру, [26]). Это, в свою очередь, может усложнить картину расщепления, следующую из Гамильтониана (8).
Неидеальное соответствие между рассчитанной и реальной картинами расщепления (см. рис. 4) может быть объяснено, по крайней мере частично, «недостающим» уровнем А2 и индуцированным давлением сдвигом низколежащих энергетических уровней Ni.
7. Выводы
Исследовалось влияние одноосного сжатия на электронные переходы ![]() иона Ni2+ (d8) в ZnO на 4216, 4240 и 4247 см-1.
Был составлен Гамильтониан давления, который удовлетворительно описывает
поведение исследуемых переходов при одноосном сжатии. Показано, что расщепление
и поляризационные свойства линий ИК поглощения согласуются с симметрией
дефекта, полученной в предшествующих работах.
иона Ni2+ (d8) в ZnO на 4216, 4240 и 4247 см-1.
Был составлен Гамильтониан давления, который удовлетворительно описывает
поведение исследуемых переходов при одноосном сжатии. Показано, что расщепление
и поляризационные свойства линий ИК поглощения согласуются с симметрией
дефекта, полученной в предшествующих работах.
Работа выполнена при поддержке Министерства образования и науки РФ (соглашения № 8514 и № 8862).
Литература
1. Klingshirn C. ZnO: From basics towards applications //Phys. Status Solidi B. 2007. № 244. P. 3027.
2. Dietl T., Ohno H., Matsukura F., Cibert J., Ferrand D. Zener Model Description of Ferromagnetism in Zinc-Blende Magnetic Semiconductors //Science. 2000. № 287. P. 1019.
3. Risbud A.S., Spaldin N.A., Chen Z.Q., Stemmer S., Seshadri R. Magnetism in polycrystalline cobalt-substituted zinc oxide //Phys. Rev. B. 2003. № 68. P. 205202.
4. Norton D.P., Overberg M.E., Pearton S.J., Pruessner K., Budai J.D., Boatner L.A., Chisholm M. F., Lee J.S., Khim Z.G., Park Y. D. Ferromagnetism in cobalt-implanted ZnO //Appl. Phys. Lett. 2003. № 83. P. 5488.
5. Jedrecy N., von Bardeleben H.J., Zheng Y., Cantin J.-L. Electron paramagnetic resonance study of Zn1-xCoxO: A predicted high-temperature ferromagnetic semiconductor //Phys. Rev. B. 2004. № 69, 041308.
6. Wardle M.G., Goss J.P., Briddon P. R. Theory of Fe, Co, Ni, Cu, and their complexes with hydrogen in ZnO //Phys. Rev. B. 2005. № 72. P. 155108.
7. Schulz H.-J., Thiede M. Optical spectroscopy of 3d7 and 3d8 impurity configurations in a wide-gap semiconductor (ZnO:Co,Ni,Cu) //Phys. Rev. B. 1987. № 35. P. 18.
8. Anderson R. S. Lattice-Vibration Effects in the Spectra of ZnO:Ni and ZnO:Co //Phys. Rev. 1967. № 164. P. 398.
9. Lavrov E.V., Börrnert F., Weber J. Dominant hydrogen-oxygen complex in hydrothermally grown ZnO //Phys. Rev. B. 2005. № 71. P. 035205.
10. Limpijumnong S., Zhang S. B. Resolving hydrogen binding sites by pressure—A first-principles prediction for ZnO //Appl. Phys. Lett. 2005. № 86. P. 151910.
11. Jokela S.J., McCluskey M. D. Structure and stability of O-H donors in ZnO from high-pressure and infrared spectroscopy //Phys. Rev. B. 2005. № 72. P. 113201.
12. Wardle M.G., Goss J.P., Briddon P.R. Relationship between binding site and pressure dependence for defect-hydrogen complexes in ZnO //Appl. Phys. Lett. 2006. № 88. P 261906.
13. Lavrov E.V., J. Weber J. Effect of uniaxial stress on vibrational modes of hydrogen in ZnO //Phys. Rev. B. 2006. № 73. P 035208.
14. Lavrov E.V., Weber J. Uniaxial stress study of the Cu–H complex in ZnO //Phys. Status Solidi B. 2006. № 243. P. 2657.
15. Lavrov E.V., Weber J., Börrnert F. Copper dihydrogen complex in ZnO //Phys. Rev. B. 2008. № 77. P. 155209.
16. Helbig R. Über die züchtung von grösseren reinen und dotierten ZnO-kristallen aus der gasphase //J. Cryst. Growth. 1972. № 15. P. 25
17. Weakliem H.A. Optical Spectra of Ni2+, Co2+, and Cu2+ in Tetrahedral Sites in Crystals //J. Chem. Phys. 1962. № 36. P. 2117.
18. Dietz R.E., Kamimura H., Sturge M.D., Yariv A. Electronic Structure of Copper Impurities in ZnO //Phys. Rev. 1963. № 132, P. 1559.
19. Dingle R. Luminescent Transitions Associated With Divalent Copper Impurities and the Green Emission from Semiconducting Zinc Oxide //Phys. Rev. Lett. 1969. № 23. P. 579.
20. Vlasenko L.S., Watkins G.D., Helbig R. Origin of the 6885-cm-1 luminescence lines in ZnO: Vanadium versus copper //Phys. Rev. B. 2005. № 71. P. 115205.
21. Shannon R.D., Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides //Acta Crystallogr. 1976. № A 32. P. 751.
22. Dresselhaus M.S., Dresselhaus G., Jorio A. Group Theory: Application to the Physics of Condensed Matter. Berlin, Heidelberg. Springer-Verlag. 2008.
23. Kaufmann U., Koidl P., Schirmer O.F. Near infrared absorption of Ni2+ in ZnO and ZnS: dynamic Jahn-Teller effect in the 3T2 state //J. Phys. C: Solid State Phys. 1973. № 6. P. 310.
24. Koidl P. Optical absorption of Co2+ in ZnO //Phys. Rev. B. 1977. № 15. P. 2493.
25. McGlynn E., Henry M.O. Splitting of point defect energy levels in wurtzite crystals under uniaxial stresses applied along arbitrary directions //Phys. Rev. B. 2007. № 76. P. 184109.
26. Brumage W.H., Lin C.C. Magnetic Susceptibilities of Transition Elements in Host Crystals. II. Ni2+ in ZnO and CdS //Phys. Rev. 1964. № 134. P. A950.