Коррекция пространственного спектра, искаженного оптической системой, с помощью метода опорного изображения. Часть 1. Классический метод опорного изображения (МОИ).

УДК 621.396

Коррекция пространственного спектра, искаженного оптической системой, с помощью метода опорного изображения.

Часть 1. Классический метод опорного изображения (МОИ).

Ю. В. Гуляев, А. Ю. Зражевский, А. В. Кокошкин, В. А. Коротков, В. А. Черепенин

Институт радиотехники и электроники им. В.А. Котельникова РАН

Статья получена 27 ноября 2013 г.

Аннотация. Методами численного моделирования проанализирован предложенный нами ранее способ улучшения качества радиотепловых изображений ММ диапазона волн, использующий априорную информацию о статистических характеристиках спектров объектов аналогичного класса и известной аппаратной функции системы.

Ключевые слова: радиоизображения, статистические характеристики спектров, пространственное разрешение.

Abstract: The method of improving the quality of the radiothermal images of MM wave range, which uses a priory information about statistical spectrum characteristics of the same class objects and known hardware system function is analyzed by a method of numerical simulation.

Key words: radio image, statistical characteristics of the spectra, the spatial resolution.

Радиоизображения, получаемые в ММ диапазоне, заметно отличаются по качеству от оптических изображений [1,3,4,6]. В основном эти отличия обусловлены малой величиной, выраженной в длине волны, апертуры оптической системы. Свой вклад в изменение полученного радиоизображения вносят и шумы измерительной аппаратуры, неблагоприятные условия наблюдения и несовершенство формирующей изображение оптической системы.

Для компенсации этих изменений применяются различные методы [1,3]. Одна из основных задач, связанных с использованием этих методов, состоит в определении параметров всех шумов (помех), влияющих на приемный сигнал. Однако на практике обычно ограничиваются некими «разумными» предположениями о характере и параметрах возникающих шумов.

В данной работе применяется альтернативный метод [2,7], не требующий знания шумов, влияющих на принимаемый сигнал. Этот метод опорного изображения (МОИ) основан на том, что пространственный спектр изображения имеет некоторые свойства, коренным образом отличающиеся от пространственных спектров шумов, искажающих полученное изображение. Ранее [2,5,7] этот метод применялся для решения задач восстановления изображений и проводилась оценка качества восстановления изображений при различных мешающих факторах, но углублённого исследования особенностей, проблем и возможностей этого метода не проводилось. Именно этим исследованиям и посвящена эта работа.

Большую часть процессов, влияющих на формирование радиоизображения, можно описать в рамках уравнения свертки [1] :

= , (1)

где D – область наблюдения, - элементарная площадка в точке (x,y), - аппаратная функция (АФ) системы, - , исходное изображение,- изображение на выходе этой системы.

Если перейти к спектральным представлениям изображений: исходного и на выходе системы :

(2)

и модуляционной передаточной функции антенны (МПФА)

, (3)

то в частотной области пространственный спектр изображения на выходе системы выражается через спектр исходного изображения и :

Откуда следует, что если известна , восстановленный спектр исходного изображения можно получить по формуле инверсной фильтрации:

= / , (4)

после чего «восстановленное» изображение рассчитывается по формуле обратного Фурье-преобразования:

. (5)

Однако результат этих действий обычно отрицательный. Причем этот результат обеспечивается не только ошибками в определении АФ и изображении на выходе системы, но и неизбежными ошибками вычислений. В работе [2] предлагается перед использованием (5) скорректировать вычисленный в (4) пространственный спектр изображения. Эта коррекция, которая составляет суть метода опорного изображения (МОИ), производится следующим образом.

Алгоритм работы метода опорного изображения (МОИ):

1. Выберем в качестве опорного изображения полутоновое изображение желательно с похожей пространственной структурой. Вычислим амплитудный спектр опорного изображения (СОИ). Разбиваем пространство частот этого спектра на 2 области. Первая, размером 9х9 пикселов от нулевой частоты, соответствует низким, а вторая, содержащая все остальные пикселы, - высоким пространственным частотам. Во второй области организуется плавающее окно усреднения (размером 5 на 5 пикселов), в котором рассчитываются статистические характеристики СОИ: среднее - m и среднеквадратичное отклонение (СКО) - s.

2. Для ликвидации ложных выбросов значений амплитуд в высокочастотной области , используя СОИ, производим процедуру фильтрации спектра , а именно, в текущем окне каждое значение сравниваем с величиной порога опорного спектра n = m+a×s, где a - варьируемый коэффициент. Если > n, то значение в «восстанавливаемом» спектре заменяется на n. Этот новый спектр назовем усредненным спектром опорного изображения (УСО).

После такой коррекции спектра, используя (5), вычислим само изображение.

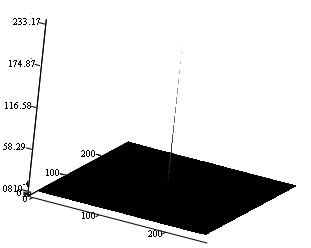
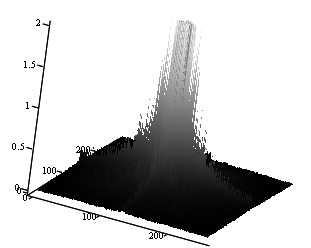
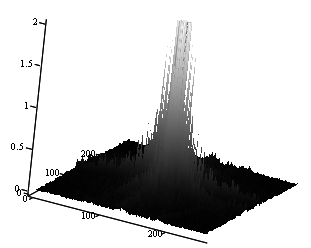
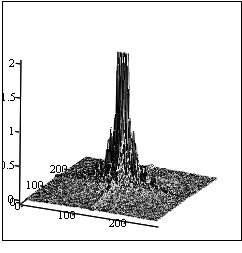
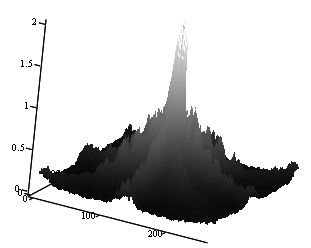
На рис. 1. показан, в линейном масштабе, типичный вид пространственного амплитудного спектра полутонового изображения. Рисунки 2 – 4 иллюстрируют несколько изображений и соответствующих им спектров, причём, для того, чтобы лучше была видна высокочастотная составляющая спектров, масштаб ограничен по вертикали (по амплитуде) величиной равной 2.

Рисунок 1. Вид типичного пространственного амплитудного спектра полутонового изображения в линейном масштабе
(средняя яркость (нулевая гармоника) в середине).

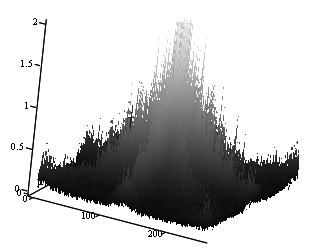
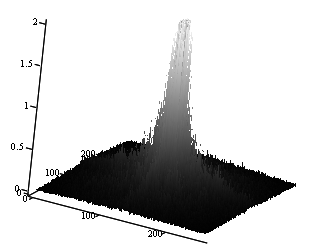
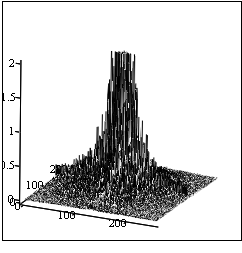
Рассмотрим работу этого метода на примерах. Рассмотрим несколько изображений и их пространственные амплитудные спектры. Для наглядности ограничим вертикальную компоненту величиной равной 2.

А Б

Рис. 2. А) Тестовое изображение букв (Шаблон); Б) Вид пространственного амплитудного спектра этого изображения с ограниченным масштабом по вертикали (амплитуде) (средняя яркость (нулевая гармоника) в середине), линейный масштаб.

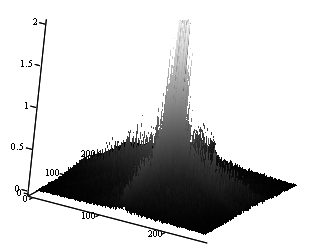
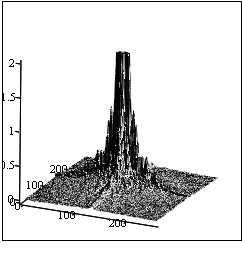
А Б
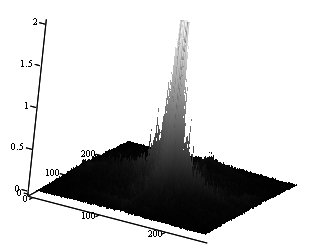
Рис. 3. А) Полутоновое изображение пистолета на фоне бронежилета; Б) Вид пространственного амплитудного спектра этого изображения с ограниченным масштабом по вертикали (амплитуде) (средняя яркость (нулевая гармоника) в середине), линейный масштаб.

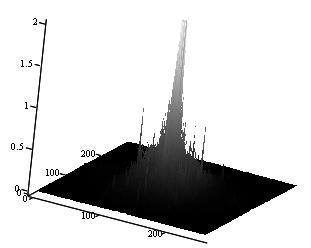
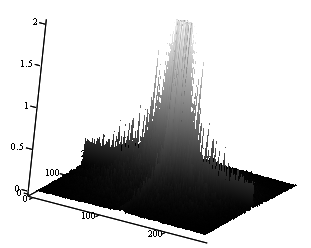
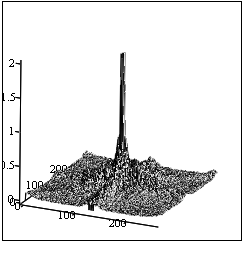
Рис. 4. А) Полутоновое изображение царя Шумера и Аккада Саргона Древнего (конец 24 – начало 23 вв. до н.э.);
Б) Вид пространственного амплитудного спектра этого изображения с ограниченным масштабом по вертикали (амплитуде)
(средняя яркость (нулевая гармоника) в середине), линейный масштаб.

Рис.5. А) Полутоновое изображение танка «Абрамс» США;
Б) Вид пространственного амплитудного спектра этого изображения с ограниченным масштабом по вертикали (амплитуде)
(средняя яркость (нулевая гармоника) в середине), линейный масштаб.

Рис.6. А) Полутоновое изображение «волнения в Париже 1968 год»;
Б) Вид пространственного амплитудного спектра этого изображения с ограниченным масштабом по вертикали (амплитуде)
(средняя яркость (нулевая гармоника) в середине), линейный масштаб.

Рис.7. А) Полутоновое изображение «досмотр на вокзале»;
Б) Вид пространственного амплитудного спектра этого изображения с ограниченным масштабом по вертикали (амплитуде)
(средняя яркость (нулевая гармоника) в середине), линейный масштаб.

Рис. 8. А) Полутоновое изображение танка «Тигр»;
Б) Вид пространственного амплитудного спектра этого изображения с ограниченным масштабом по вертикали (амплитуде)
(средняя яркость (нулевая гармоника) в середине), линейный масштаб.

Рис. 9. А) Полутоновое изображение автомашины «УАЗ»;
Б) Вид пространственного амплитудного спектра этого изображения с ограниченным масштабом по вертикали (амплитуде
(средняя яркость (нулевая гармоника) в середине), линейный масштаб.

Сравнивая между собой спектры разных изображений, можно сделать вывод о том, что у этих спектров есть общее свойство – амплитуда максимальна при нулевой частоте и быстро уменьшается при ее увеличении. Достаточно хорошо проявляются и индивидуальные свойства спектров – разная изрезанность и специфичный рельеф в виде «оврагов» и «гребней».

После прохождения через оптическую систему вид спектров меняется. Для определенности будем использовать аппаратную функцию Гауссова вида:

В дальнейшем при расчетах примем . Изображение букв и спектр на рис. 2 примут, например, следующий вид, приведенный на рис. 10.

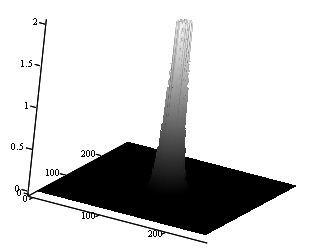
Рис. 10. При S=6. А) Изображение букв; Б) Вид пространственного амплитудного спектра
этого изображения с ограниченным масштабом по вертикали (амплитуде)
(средняя яркость (нулевая гармоника) в середине), линейный масштаб.

На рис.10. хорошо видно, что за счет того, что амплитуда спектра на высоких частотах стала очень малой, буквы на рис. 10А. стали слабо распознаваемы.

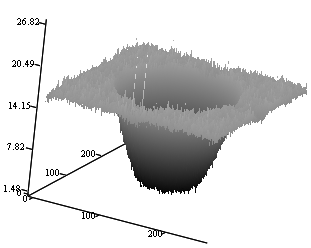
Применение инверсной фильтрации – рис. 11. - не приводит к восстановлению исходного изображения. Из-за появления больших высокочастотных выбросов амплитуды спектра полностью разрушилось восстановленное из него изображение.

Рис. 11. Результат инверсной фильтрации. А) Изображение букв; Б) Вид пространственного амплитудного спектра
этого изображения (средняя яркость (нулевая гармоника) в середине), в логарифмическом масштабе.

Для того, чтобы можно было сравнивать разные амплитудные спектры, будем использовать не объемные рисунки, а разрезы вдоль главной диагонали - . Такой выбор направления разреза обусловлен следующим соображением – в силу того, что у изображений как правило есть элементы, расположенные преимущественно вертикально и горизонтально, то и на спектре эти направления будут особенными. Мы же анализируем в первую очередь общие, а не особенные закономерности. В спектрах на рис. 2-12. хорошо заметна эта особенность спектров. На рис. 2, в силу того, что часть букв повернута под 45 градусов, диагональное направление в спектре особенное, что заметно на спектре. На разрезах мы будем рисовать графики не амплитуды спектра, а его логарифм. Понятно, что это делается из-за большого диапазона изменения амплитуды спектра. На рис. 12. представлены графики диагональных разрезов амплитудных спектров исходного, прошедшего через оптическую систему, инверсно отфильтрованного и опорного изображений.

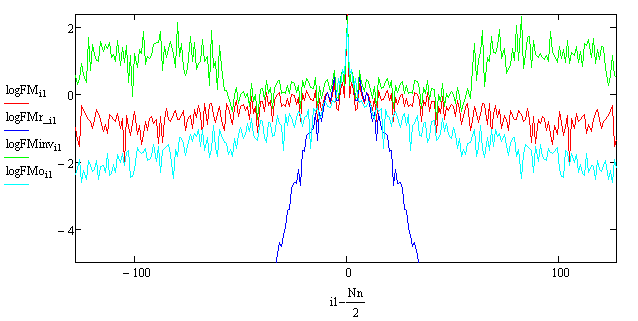
Рис. 12. Графики, в логарифмическом масштабе, диагональных разрезов амплитудных спектров изображений: исходного - - красный; прошедшего через оптическую систему - - синий; инверсно отфильтрованного - - зеленый; опорного - - голубой.

Сравнение графиков на рис. 12. позволяет заключить, что после прохождения через оптическую систему спектр исходного изображения – красная линия потерял часть высоких частот – синяя линия. Инверсная фильтрация позволяет восстановить (частично) высокие частоты и поведение графиков спектров после инверсной фильтрации – зеленая линия и исходного – красная линия в диапазоне частот от -50 до 50 одинаково. Однако за пределами этого диапазона поведение инверсно отфильтрованного спектра сильно отличается от исходного. Это объясняется влиянием ошибок вычислений. Поведение графиков спектров исходного изображения – красная линия походит на поведение спектра выбранного опорного изображения – рис. 5 – голубая линия.

Использование схожести поведений амплитудных спектров и лежит в основе МОИ. Однако непосредственное использование спектра опорного изображения неразумно из-за сильной изрезанности его, причем эта изрезанность спектров разных изображений существенно разная. В качестве образца (опоры) используется так называемый усредненный спектр, являющийся комбинацией среднего значения амплитудного спектра по выбранному спрайту и среднеквадратичного отклонения по этому же спрайту с неким коэффициентом. Величину его мы определили равной 4 по рекомендации [2].

Применим МОИ. Для этого в качестве опорного выберем например изображение на рис. 5. Выбор исходного тестового изображения не случаен. В силу того, что амплитудный спектр рис. 2Б. сильно отличается от остальных спектров рис. 3-9, следует ожидать больших трудностей в восстановлении именно изображения на рис. 2. Кроме этого наличие однородного белого фона, на котором находятся черные буквы позволяет легче увидеть артефакты на восстановленном изображении, являющиеся следствием примененного метода МОИ. Результат применения МОИ представлен на рис. 13.

Рис. 13. Результат применения МОИ. А) Изображение букв; Б) Вид пространственного амплитудного спектра этого изображения с ограниченным масштабом по вертикали (амплитуде) (средняя яркость (нулевая гармоника) в середине), линейный масштаб.

Как видно на рис. 13, изображения букв восстановились, однако спектр на рис. 13Б не похож на исходный спектр на рис. 2Б. Очевидно, что это объясняется выбором опорного изображения. Однако спектр на рис. 13Б только отдаленно напоминает спектр опорного изображения на рис. 5Б. Но в МОИ используется не просто амплитудный спектр опорного изображения, а усредненный спектр - УСО, описанный выше. На рис. 14 приведены спектр и усредненный спектр опорного изображения с ограниченным масштабом по вертикали.

Рис. 14. Вид пространственных амплитудных спектров с ограниченным масштабом по вертикали (амплитуде) (средняя яркость (нулевая гармоника) в середине), линейный масштаб: А) спектр опорного изображения (Рис. 2); Б) усредненный спектр опорного изображения (УСО).

Из сравнения спектров на рис. 13Б и на рис. 14Б следует их очевидная похожесть.

Проанализируем применение МОИ с помощью разрезов спектров на рис. 15.

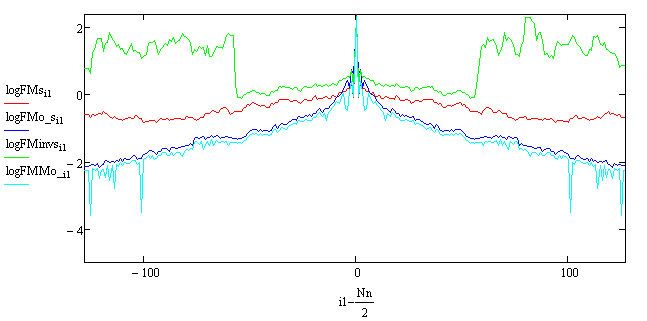
Рис. 15. Графики диагональных разрезов усредненных амплитудных спектров исходного - - красный, опорного - - синий, инверсно отфильтрованного - - зеленый и амплитудного спектра восстановленного МОИ - - голубой.

Из рис.15 следует, что, как и на рис. 12, поведение усредненных и амплитудных спектров исходного и инверсно отфильтрованного одинаково в диапазоне частот от -50 до 50. Вне этого диапазона их поведение разное. Поведение усредненных спектров исходного и опорного изображений вне окрестности нулевой частоты несколько разное – величина усредненного спектра опорного изображения падает быстрее с увеличением модуля частоты, чем величина усредненного спектра исходного изображения. Причиной этого в первую очередь является тот факт, что диагональное направление для исходного изображения является особым в отличие от опорного изображения. Графики, соответствующие восстановленному МОИ спектру и усредненному опорному спектру, очень похожи из-за механизма применения МОИ.

Понятно, что выбор опорного изображения скажется на качестве восстановления. Однако ожидать идеального результата даже при выборе в качестве опорного самого исходного изображения не стоит. Проверим это. На рис. 16. представлены результаты применения МОИ при выборе в качестве опорного изображения рис. 2. Сравнение рис. 13А и рис. 16А показывает, что за счет выбора исходного изображения в качестве опорного изображения удалось улучшить качество восстановления. Но идеального восстановления достигнуть не удалось. Конечно, играют свою роль и потери информации за счет ошибок вычислений, но главным здесь является влияние отличия УСО от спектра исходного изображения.

Рис. 16. Результат применения МОИ. А) Изображение букв; Б) Вид пространственного амплитудного спектра этого изображения с ограниченным масштабом по вертикали (амплитуде) (средняя яркость (нулевая гармоника) в середине), линейный масштаб.

На рис. 17. представлены амплитудный спектр и усредненный спектр опорного изображения. Видно, что эти спектры отличаются друг от друга за счет проведенной операции усреднения. Поэтому и спектр полученного МОИ изображения – рис. 16Б отличается от спектра исходного – рис. 2Б.

Рис. 17. Ограниченные по амплитуде пространственные спектры в линейном масштабе: А) опорного изображения (Рис. 1); Б) усредненный спектр опорного изображения (УСО).

Выводы

1.Амплитудные спектры изображений имеют общие черты и индивидуальные особенности. К индивидуальным особенностям можно отнести изрезанность спектра и наличие «гребней» и «оврагов». Общие черты заключаются в определенной симметрии спектров и вполне устойчивой закономерности поведения усредненной амплитуды от пространственной частоты.

2.Использование общей закономерности поведения спектра позволяет МОИ восстанавливать изображения после инверсной фильтрации.

3.Качество восстановления изображения зависит в том числе и от выбора опорного изображения. Однако даже выбор в качестве опорного самого исходного изображения не гарантирует идеального результата. Большую роль может играть отличие усредненного спектра опорного изображения от спектра исходного изображения.

4.Отличие аппаратной функции, используемой в инверсной фильтрации, от реальной может заметно осложнить восстановление изображение с помощью классического МОИ [5] .

Литература

1. Р. Гонсалес, Р. Вудс. Цифровая обработка изображений. М. «Техносфера» , 2005, 1071 стр.

2. Зражевский А.Ю., Кокошкин А.В., Новичихин Е.П., Титов С.В., «Повышение качества радиоизображений». «Нелинейный Мир», № 9, 2010г., с. 582-590.

3. Тихонов А.Н., Арсенин В.Я. - Методы решения некорректных задач. М.Наука, 1979.

4. Зражевский А.Ю., Голунов В.А, Смирнов М.Т., Новичихин Е.П., Лоскутов В.С., Ермаков Д.М. Поляризационные радиотепловые портреты.

5. А.Ю. Зражевский, А.В. Кокошкин, Влияние уровня боковых лепестков аппаратной функции на качество восстановленного изображения. «Журнал радиоэлектроники» [электронный журнал]. 2013. №4. URL: http://jre.cplire.ru/jre/apr13/8/text.html

6. В.А. Голунов, Г.К.Загорин, А.Ю. Зражевский, Б.А. Розанов, А.В. Соколов, Л.Ф. Черная. Пассивная радиолокация на миллиметровых волнах. В кн. Вопросы перспективной радиолокации. М., Изд. «Радиотехника», 2003, с. 393-463.

7. А.Ю. Зражевский, В.А. Коротков. Особенности восстановления искаженного оптической системой радиоизображения с помощью метода опорного изображения. «Журнал Радиоэлектроники» [электронный журнал]. 2013. №4. URL: http://jre.cplire.ru/jre/apr13/3/text.html