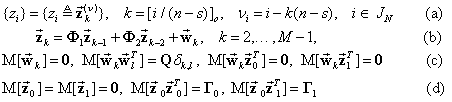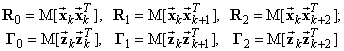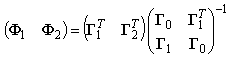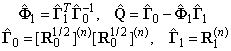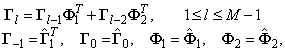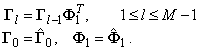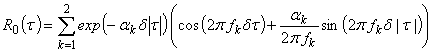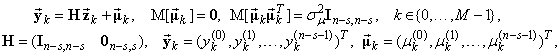ПРЕДСТАВЛЕНИЕ СЛУЧАЙНЫХ ПРОЦЕССОВ ВЕКТОРНОЙ РЕКУРРЕНТНОЙ ЦИРКУЛЯНТНОЙ

МОДЕЛЬЮ ВТОРОГО ПОРЯДКА

В. П. Волчков, Н. Е. Поборчая, А. М. Шлома

Московский технический университет связи и информатики (МТУСИ)

Статья получена 12 декабря 2013 г.

Аннотация. Одной из приоритетных задач цифровой обработки сигналов является уменьшение вычислительной сложности соответствующих алгоритмов, но без значительных потерь их точности. Для синтеза таких алгоритмов нужны хорошие адекватные модели сигналов. В работе для представления случайных сигналов предлагается использовать векторную рекуррентную циркулянтную модель второго порядка. Получены алгоритм вычисления параметров такой модели по заданной корреляционной функции сигнала и выражения для корреляционной функции аппроксимирующего процесса. Проведен сравнительный анализ качества аппроксимации с другими известными моделями. Построены оптимальные рекуррентные алгоритмы фильтрации и сглаживания. Экспериментально исследованы точностные характеристики этих алгоритмов, подтверждающие их высокую эффективность. Основные результаты данной статьи докладывались на 6-ой Всероссийской научно-технической конференции «Радиолокация и радиосвязь»

Ключевые слова: случайный сигнал, случайный процесс, оптимальная оценка, фильтр Калмана, фильтр Винера, авторегрессионная модель, циркулянтная модель, стохастическое разностное уравнение, корреляционная функция, преобразование Фурье.

Abstract. One of а foreground task of digital signal processing is a decrease of computational complexity of appropriate algorithms, but without substantial loss accuracy. Good adequate signal models are necessary for synthesis of these algorithms. In the article, the vectorial recurrent circulant model of the second dynamic order is proposed for random signals representation. For given correlation function of signal the computational procedures of parameters this model and expression of approximating correlation function are derived. The comparative analysis of approximation property of the proposal model and other known models are executed. Optimal recurrent algorithms of filtration and smoothing based on the proposal model are produced. Accuracy behavior and efficiency of these algorithms are confirmed in experimental research. 

Key words: random process, random signal, optimal estimate, Kalman filter, Winner filter, circulant model, autoregressive model, stochastic difference equalization, correlation function, Fourier transform.

 

1.                Введение

При цифровой обработке сигналов и изображений в радиолокации и связи часто возникает необходимость в наилучшей аппроксимации наблюдаемого случайного процесса дискретной динамической моделью определенного порядка. Причем модель должна быть такой, чтобы в дальнейшем ее можно было использовать для эффективного решения задач сглаживания, параметрического спектрального анализа, обнаружения, распознавания и др. Под эффективностью мы здесь понимаем не только простую структуру получаемых оптимальных алгоритмов обработки, но и одновременно возможность их быстрой вычислительной реализации. Для многих известных динамических моделей, например, авторегрессии или  авторегрессии-скользящего среднего [1], последнее может служить ограничительным фактором их применения, если динамический порядок модели  велик. В результате разработчикам часто приходится «деформировать» полученный оптимальный алгоритм с целью его упрощения, но при этом, естественно, теряются и его оптимальные свойства. В данной работе указанное противоречие предлагается разрешить, строя оптимальный синтез алгоритмов на заранее подходящем классе моделей сигналов, который, с одной стороны, достаточно широк, чтобы обеспечить хорошую аппроксимацию реальных сигналов, а, с другой стороны, позволяет получить эффективную реализацию полученных алгоритмов. Для этой цели используется подход [2], при котором для синтеза выбирается класс аппроксимирующих динамических моделей сигналов, обладающих свойством симметрии (инвариантности) по отношению к конечной группе циркулянтных преобразований. Эта группа действует на вектор состояния динамической модели в некотором скользящем временном окне  размера  и обеспечивает в этом окне наилучшую аппроксимацию исходного случайного процесса. Аппроксимирующие свойства вне данного окна будут зависеть от параметра зацепления  соседних скользящих окон и динамического порядка модели. В данной работе порядок динамической аппроксимации  увеличен до двух, что позволило улучшить ее аппроксимирующие свойства, по сравнению с аналогичной моделью, описанной в [2]. Кроме того, показано, что при одном и том же динамическом порядке , применение рекуррентных моделей скользящего окна вместо известных авторегрессионных моделей обеспечивает лучшую аппроксимацию случайного процесса и более адекватные спектральные оценки. В то же время установлено, что циркулянтная симметрия векторной рекуррентной модели позволяет диагонализировать структуру матриц, входящих в соответствующий оптимальный алгоритм сглаживания и упростить его вычислительную реализацию. Для этого достаточно применить к этой модели -точечное дискретное преобразование Фурье (ДПФ), т.е перейти к базису ее собственных функций. Для предложенной векторной рекуррентной модели второго порядка получены алгоритм вычисления ее оптимальных параметров по заданной корреляционной функции сигнала и выражения для корреляционной функции аппроксимирующего процесса. Определены критерии качества аппроксимации и по ним проведен сравнительный анализ с другими известными моделями. На основе предложенной модели построены оптимальные рекуррентные алгоритмы фильтрации и сглаживания во временной и спектральной областях. Экспериментально исследованы точностные характеристики этих алгоритмов, подтверждающие их высокую эффективность.

 

2.   Рекуррентная циркулянтная аппроксимация 2-го порядка случайного процесса с известной корреляционной функцией

Пусть случайный сигнал представляет вещественную последовательность

                                        ,                                            (1)

полученную в результате дискретизации по времени непрерывного стационарного (в широком смысле) случайного процесса  на конечном интервале . При этом сигнал (1) имеет нулевое математическое ожидание и известную корреляционную функцию

                                 , ,                                           (2)

где ,  – оператор математического ожидания. Аппроксимируем последовательность  другим вещественным стационарным случайным сигналом , который описывается векторным стохастическим разностным уравнением [3]:

                              (3)

Здесь  – n-мерный вектор, заданный в скользящем временном окне, , , ;  , , ,  – натуральные числа;  – показывает, сколько общих элементов у соседних векторов (параметр зацепления); ;  – оператор взятия целой части числа;  – округление до ближайшего целого ;  – символ Кронекера;  – n-мерный вектор формирующего шума. Параметры модели ,   – вещественные циркулянтные матрицы размерности , причем  – невырожденная. Запись ,  в (3a) означает, что -ое значение аппроксимирующего процесса  является -ой компонентой вектора , т.е. процедура распаковки векторного процесса (3) сводится к последовательному выстраиванию векторов  в один столбец: . Модель (3) будем называть рекуррентной циркулянтной n-моделью 2-го порядка. Фактически, она является дальнейшим развитием аналогичной модели 1-го порядка, приведенной в [2].

Напомним [4], что элементы любой циркулянтной - матрицы ,  удовлетворяют условию , (где «» – вычитание по модулю ). Семейство  всех таких матриц образует линейное коммутативное подпространство евклидового пространства  квадратных -матриц со скалярным произведением и нормой

                     ,          ,        .       

Обозначим , тогда задача наилучшей аппроксимации сводится к нахождению оптимальных параметров  модели (3) по критерию минимума среднего квадрата ошибки (СКО)

                     ,                                       (4)

 

Определим корреляционные матрицы векторных стационарных случайных процессов  и :

                                (5)

 

Нетрудно убедиться, что , . Если взять ковариации ,  от обеих частей равенства (e33) и учесть  и (5), то получим

                                                      (6)

                                             ,                                                  (7)

                                             .                                                 (8)

Уравнения (6)-(8) можно записать в следующем виде

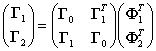,       , тогда

                                  ,                                           (9)

               .                              (10)

 

Определим симметрические квадратные корни корреляционных матриц  

                                           ,.                                                       (11)

Тогда справедливы представления , , где  – случайный вектор, , а выражение для ошибки аппроксимации  в скользящем временном окне  и критерий (4) преобразуются к виду
            ,  

                                    ,  

где запись  в неявном виде указывает на зависимость от матричных параметров модели (3). Следовательно, оптимальное решение  данной экстремальной задачи является проекцией матрицы  на евклидовое подпространство циркулянтных матриц . Это решение единственное и определяется выражением [5]:

                                            ,                               (12)

где  – оператор ортогонального проектирования на подпространство ;  – циркулянтная матрица перестановок размерности , множество степеней которых  образует ортогональный базис в .

Пусть   – корреляционные матрицы векторного процесса (3), удовлетворяющего критерию (4), и покажем, что все они могут быть вычислены из исходных корреляционных матриц  с помощью преобразования (12). Используя представление , имеем . Отсюда при  с учетом (11),(12)

                                         .                                       (13)

Если , воспользуемся известными [5] свойствами оператора :

,    ,     ,

и выполним тождественные преобразования  , т.е.

                                              .                                               (14)

Таким образом, алгоритм наилучшей, по критерию (4), аппроксимации стационарного случайного процесса (1) рекуррентной циркулянтной моделью 2-го порядка (3) состоит в следующем. Сначала по заданной корреляционной функции (2) строятся корреляционные матрицы , затем по формулам (13), (14) вычисляются , с помощью которых по (9) и (10) определяются матричные параметры  модели (3).

Заметим, что описанные в [2] рекуррентная циркулянтная модель 1-го порядка и ее алгоритм идентификации могут быть получены из формул (6)-(8), (13),(14), если в них положить . Соответствующие выражения имеют вид

                                                                          (15)

 

 Наконец, нерекуррентная циркулянтная модель [5], описывающая N-стационарный случайный процесс, может рассматриваться как рекуррентная модель 0-го порядка, получаемая из (3), если в ней положить , , , при этом

          ,                    (16)

где  – корреляционная функция (2) исходного процесса. Отметим, что процедуры оценивания параметров рекуррентных моделей (9)-(10), (15) не зависят от . Поэтому они будут справедливы и на бесконечном интервале представления сигнала.

 

3. Корреляционная функция аппроксимирующего процесса и ее особенности

Пусть аппроксимирующий процесс  описывается рекуррентной моделью (3), а его параметры выбраны по описанному выше алгоритму идентификации. Тогда его корреляционную функцию на интервале  можно представить в виде  

                                                  (17)

где  определяется (3а); ,  – корреляционная матрица векторного процесса (3b), отвечающая временному сдвигу . Если обе части уравнения (3b) умножить справа на  и определить математическое ожидание, получим

, 

Отсюда, с учетом (3c), (5) и свойства стационарности  приходим к рекуррентному уравнению

                                                               (18)

 

где начальные условия определяются формулами (13), (14), (9). Как частный случай, при  получаем аналогичные выражения для рекуррентной циркулянтной модели 1-го порядка

                                                                                 (19)

Для нерекуррентной циркулянтной модели  и с учетом (16), (17)

                                   ,                             (20)

Формулы (16)-(20) полностью определяют алгоритм вычисления корреляционной функции аппроксимирующего процесса для любой указанных циркулянтных моделей. Как следует из (17) , структура корреляционной функции сильно зависит от величины параметра зацепления . Если , имеем

                     ,                            (21)

т.е. корреляционная функция (21) имеет n-периодическую структуру, а соответствующая корреляционная матрица

                             .                              (22)

является эрмитовой блочно-теплицевой с циркулянтными блоками , , количество которых равно . Однако, при  циркулянтная структура блоков нарушается.

Все сказанное справедливо для рекуррентных циркулянтных моделей 1-го и 2-го порядка. В случае нерекуррентной модели (16) корреляционная функция (20) и соответствующая корреляционная матрица

                                                                     (23)

становятся циркулянтными.

Отметим, что специальная структура матриц (22), (23) позволяет значительно упростить вычислительные алгоритмы оптимальной обработки аппроксимирующих процессов . Для этого достаточно применить к ковариационным матрицам  унитарное блочно-диагональное преобразование подобия вида

                    (24)

приводящее  к блочно-теплицевой матрице  с диагональными блоками . (Здесь  – унитарная матрица Фурье, «» – символ эрмитового сопряжения). Mатрица  имеет разреженную структуру с большим числом нулей. Кроме того, она имеет простой и эффективный алгоритм обращения [6], причем обратная матрица  также является разреженной. В частном случае (23), преобразование (24) приводит к диагональной матрице .

 

4. Анализ аппроксимирующих свойств циркулянтных n-моделей

В разделе 1 мы фактически показали, что для стационарного случайного процесса (1) с заданной корреляционной функцией (2) наилучшим рекуррентным циркулянтным приближением 2-го порядка является процесс, описываемый стохастическим уравнением (3) с параметрами . При этом, варьируя параметром зацепления  и размером скользящего окна  можно изменять структуру циркулянтной модели (3) и ее аппроксимирующие свойства. Процедуру выбора адекватной структуры будем называть – идентификацией модели. В нашем случае она сводится к выбору таких значений  и , при которых удовлетворяется выбранный критерий качества аппроксимации (см. ниже).

Для упрощения дальнейшего изложения обозначим модель (3) с оптимально выбранными параметрами  через , аналогичную рекуррентную циркулянтную модель 1-го порядка [2] – через , нерекуррентную циркулянтную модель [5] (нулевого динамического порядка) – через . Наконец, общую модель случайного процесса (1) с произвольной корреляционной функцией (2) обозначим через . Заметим, что в частном случае модели ,  описывают известные процессы авторегрессии 1-го и 2-го порядков, у которых параметры совпадают с решением уравнений Юла-Уолкера [1].

Для сравнительного анализа аппроксимирующих свойств указанных моделей поступим следующим образом. Выберем непрерывный случайный сигнал  с известной корреляционной функцией , дискретизируем его по времени  с шагом  и запишем дискретную корреляционную функцию ,  на конечном интервале . Затем, следуя описанным в разделе 1 процедурам, аппроксимируем полученный дискретный случайный сигнал ,  циркулянтными моделями , ,  и вычислим по формулам (17)-(20) их корреляционные функции , которые обозначим , , , соответственно. Тогда для сигнала  и всех указанных его моделей можно определить соответствующие корреляционные матрицы , , , и среднеквадратически-эквивалентные случайные процессы , , , где , симметрический квадратный корень из матрицы,  – случайный N-вектор, с параметрами . Для оценки качества аппроксимации сигнала ,  циркулянтными моделями будем использовать следующие характеристики и критерии.

К1. Текущие среднеквадратические ошибки (СКО) аппроксимации  на отрезке  и усредненные по времени относительные СКО :

                    ,  ,   (25)

                     ,

где индекс  соответствует порядку аппроксимирующей циркулянтной модели,  – дисперсия значений случайного сигнала ..

К2. Спектральные плотности мощности (СПМ), которые рассчитываются по соответствующим циклическим корреляционным функциям [6, c.426]:

,      (26)

  ,          (27)

где  частотный индекс;  – спектральная плотность сигнала .

Ниже для проведения эксперимента выбран дискретный случайный сигнал  с корреляционной функцией

  ,    (28)

, , , , ,

Алгоритм идентификации рекуррентных моделей ,  состоял в следующем. Среди возможных значений параметров ,  методом перебора выбирались те, при которых текущие ошибки аппроксимации (25) оказывались минимальными, а в их поведении отсутствовала периодичность (последнее гарантирует устойчивость аппроксимирующих характеристик модели). Эксперимент показал, что для  наилучшая аппроксимация случайного сигнала с корреляционной функцией (28) у модели  достигается при , , а у модели  – при , . Если же , т. е. когда аппроксимация сигнала осуществляется в пределах размеров скользящего окна рекуррентной модели, то минимум ошибки (25) в обоих случаях достигается при , а величина этой ошибки практически одинакова.

 

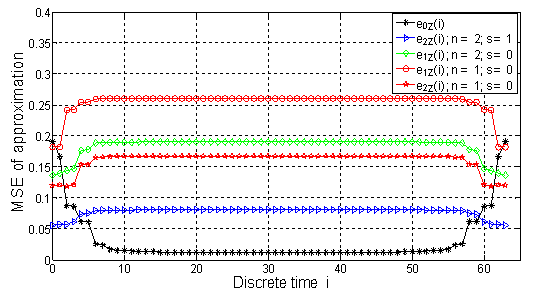
Рис. 1.   Текущие ошибки аппроксимации,

Рис. 2.  Спектр плотности мощности (PSD),

 На рис.1 и рис. 3 представлены графики текущих ошибок (25) для всех указанных значений параметров  и , а на рис.2, рис. 4  – спектральные плотности мощности (26) соответствующих аппроксимирующих процессов. Кроме того, для сравнения на этих же рисунках приведены аналогичные графики, отвечающие известным [1] авторегрессионным моделям 1-го и 2-го порядков , . Анализ этих кривых на рис.1 и рис. 2 показывает, что при  применение рекуррентных циркулянтных моделей 2-го порядка, вместо моделей 1-го порядка, позволяет улучшить аппроксимацию как во временной, так и в частотной областях. При этом средние относительные ошибки для моделей , , соответственно, равны , , а выигрыш по точности составляет . В то же время, эти модели проигрывают нерекуррентной модели , что объясняется гораздо большим числом  параметров, участвующих в описании этой модели. Кривые на этих же рисунках показывают, что модели ,  по сравнению с авторегрессионными моделями ,  того же динамического порядка обладают более хорошими аппроксимирующими свойствами. При этом для моделей , , средние относительные ошибки (25) равны , , а соответствующие проигрыши по точности составляют ,  (здесь  в нижнем индексе указывает на авторегрессионную модель). Интересно также отметить, что двухмодальность спектра исходного сигнала (кривая PSD(k) на рис.2) воспроизводится только моделью . Чтобы выявить этот факт с помощью модели авторегрессии, пришлось бы использовать модель  с динамическим порядком 4.

 

Рис. 3.   Текущие ошибки аппроксимации,

 

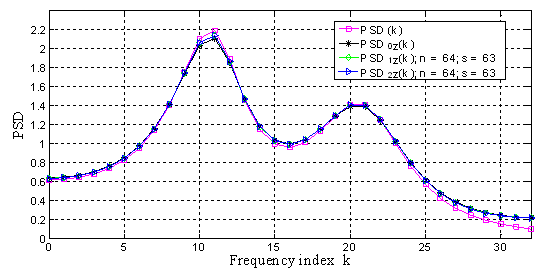
Рис. 4.  Спектр плотности мощности (PSD),

Кривые на рис.3 показывают, что при ,  (т.е. когда интервал аппроксимации сигнала совпадает с размером скользящего окна) текущие и средние ошибки (25) для моделей ,  становятся очень маленькими: . Это почти в три раза меньше , чем у нерекуррентной модели . В результате спектры PSD (26) для этих моделей на рис. 4 практически совпадают со спектром (27) исходного сигнала. Последнее имеет важное практическое значение, так как в отличие от , рекуррентные модели скользящего окна ,  являются параметрическими. Это позволяет строить на их основе эффективные алгоритмы параметрического спектрального оценивания сигналов [7],[8]. Причем, равенство ошибок  означает, что для стационарных сигналов (1) выигрыш от увеличения динамического порядка модели скользящего окна отсутствует.

Можно показать, что ситуация меняется, если анализируемый скалярный сигнал  и его дискретная аппроксимация (3a) являются нестационарными, например,  – узкополосный сигнал, у которого центральная частота изменяется во времени. Если при этом векторный аппроксимирующий процесс (3b) стационарен (в широком смысле), то все изложенное в разделе 2, касающееся нахождения оптимальных параметров модели, оказывается справедливым. Второй порядок у модели  в данном случае позволяет более адекватно описывать сигнал и синтезировать алгоритмы многоканальной частотной автоподстройки.

 

5. Применение рекуррентных циркулянтных моделей для субоптимальной фильтрации

В данном разделе будет показано, что циркулянтность и хорошие аппроксимирующие свойства модели  позволяют синтезировать эффективные вычислительные алгоритмы фильтрации и сглаживания (далее эти понятия уточняются) случайных сигналов на конечном интервале. Рассмотрим сначала применение  для субоптимальной фильтрации сигнала (1). Пусть дискретный стационарный случайный процесс  с заданной корреляционной функцией (2) наблюдается на фоне белого гауссовского шума  

                                ,                                                (29)

с параметрами , ( – символ Кронекера). Требуется, используя аппроксимацию сигнала , на основании текущей выборки  построить субоптимальную фильтрационную оценку  сигнала  по критерию минимума среднего квадрата ошибки (СКО):

                                                                             (30)

Применяя методику, описанную выше в разделе 1, аппроксимируем случайный сигнал ,  рекуррентной n-моделью (3). Тогда соответствующее векторное уравнение наблюдений принимает вид

          (31)

 

где в число наблюдаемых координат включены только те, которые по формуле (3a) непосредственно участвуют в формировании скалярного случайного сигнала . В результате субоптимальная фильтрация (30) сводится к фильтрации векторного сигнала  по критерию

                                                                                           (32)

с последующей распаковкой его оценок  в скалярный вариант по формуле

                                              (33)

Отметим, что минимум в (30) и (32) берется по всем линейным оценкам, зависящим от текущей выборки  и допускающим рекуррентную структуру .

Для уменьшения количества вычислительных операций перейдем в спектральную область, осуществив дискретное преобразование Фурье (ДПФ)

                   ,       ,      

где  – унитарная матрица Фурье; наличие звездочки «*» в нижнем индексе далее означает, что соответствующий вектор или матрица относятся к спектральной области ДПФ. Тогда (3b) и (31) преобразуются к виду:

            ,                 (34)

             ,

где согласно известному свойству циркулянтных матриц [6]  , ,  – являются диагональными. Расширяя вектор состояния, запишем (34) в следующей форме:

                                                                                (35)

                   ,         

 

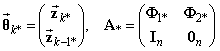В результате экстремальная задача (32) преобразуется к виду

                                                                             

и решается с помощью многомерной линейной фильтрации Калмана. Алгоритм вычисления оценок расширенного процесса  имеет вид:

         ,      

           ,                (36)

                    

 

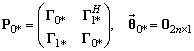
Далее, используя обратное ДПФ, возвращаемся во временную область  и осуществляем распаковку скалярных значений оценок ,  с учетом их временной расстановки внутри соответствующих векторов модели (3): , , .

Напомним, что в формулах (34)-(36) параметры рекуррентной n-модели ,  выбираются из условия наилучшей аппроксимации в соответствии с методикой, описанной выше в разделе 2, т.е. на основе известной корреляционной функции (2). Кроме того, все блочные матрицы, входящие в алгоритм (36), состоят из диагональных подматриц, что обеспечивает его вычислительную эффективность. Результаты статистического моделирования алгоритма (36) для разных аппроксимирующих моделей приводятся ниже в разделе 8.

 

6. Применение рекуррентных циркулянтных моделей для субоптимального сглаживания на закрепленном интервале

Рассмотрим теперь задачу оптимального рекуррентного сглаживания на интервале . В этом случае требуется на основании всей выборки  построить субоптимальную рекуррентную оценку n-сглаживания  сигнала  по следующему критерию минимума СКО:

                    :    ,                                            (37)

что с учетом модели (3) эквивалентно

                         :                          (38)

Отметим, что минимум в (37) и (38) берется по всем линейным оценкам , , зависящим от выборки  и допускающим рекуррентную структуру . Таким образом, оптимальные оценки n-сглаживания в каждый момент времени  учитывают гораздо больший объем информации, чем при n-фильтрации по критерию (30). Известно [9], что алгоритм оптимального сглаживания (на закрепленном интервале ) для рекуррентных марковских моделей вида (35) включает в себя фильтрацию в прямом времени, а затем дополнительное сглаживание фильтрованных оценок в обратном времени. Поэтому с учетом полученного ранее алгоритма n-фильтрации (36), алгоритм n-сглаживания в спектральной области принимает вид

                                                        (39)

                               ,        

                        Нач. усл.:           

Здесь  – оценки фильтрации и сглаживания расширенного вектора n-модели (35), соответственно; ,  ковариационные матрицы ошибок фильтрации и экстраполяции из алгоритма (36);  – матрицы ошибок сглаживания.

Далее, используя обратное ДПФ, возвращаемся во временную область , выделяем в полученном векторе 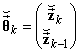 первую компоненту  и осуществляем распаковку скалярных сглаженных оценок ,  с учетом их временной расстановки внутри векторов , , .

Отметим, что для любой из перечисленных выше аппроксимирующих моделей , ,  сглаживание по критерию (38) может быть выполнено с помощью нерекуррентного фильтра Винера [10]:

                             ,       ,                               (40)

где  – вектор аппроксимирующего процесса , отвечающий рекуррентной модели m-го порядка;  – его корреляционная матрица (22) или (23);  – соответствующий вектор оценок сглаживания,  – вектор наблюдаемого процесса (29). В частности, при  алгоритм (40) соответствует аппроксимирующей модели  и эквивалентен рекуррентному алгоритму (39). Для исходного процесса (1) в виде вектора  с корреляционной матрицей ,  алгоритм оптимального сглаживания Винера имеет аналогичный вид

                 , ,                                        (41)

где  – вектор сглаженных оценок,  – ковариационная матрица апостериорных ошибок сглаживания.

При больших  cпециальная блочная структура корреляционной матрицы  (особенно в случае нулевого параметра зацепления ) позволяет значительно упростить вычислительную реализацию алгоритма сглаживания (41), если применить к нему унитарное спектральное преобразование  из формулы (24):

                                    ,                               (42)

Как уже отмечалось в разделе 2, матрицы ,  сильно разреженные, причем процедура матричного обращения допускает эффективную вычислительную реализацию. В частном случае, для циркулянтной модели  (при ) все матрицы в алгоритме (42) будут диагональными. Для возвращения во временную область и получения сглаженных оценок , достаточно применить к спектральным оценкам (42) обратное преобразование .

Таким образом, в спектральной области нерекуррентный алгоритм сглаживания Винера для аппроксимирующих процессов ,  может оказаться более предпочтительным, чем рекуррентный . На практике, фильтр Винера (42) целесообразно применять, если , а . Для больших значений , которые, например, характерны для задач обработки изображений, рекуррентный алгоритм сглаживания (39) более целесообразен, поскольку его реализация требует меньшего объема оперативной памяти и позволяет рекуррентно следить за качеством получаемых оценок.

 

7. Экспериментальное исследование полученных алгоритмов фильтрации и сглаживания

Статистическое моделирование алгоритмов фильтрации и сглаживания выполнялось с использованием пакета прикладных программ MATLAB. Для имитации входного сигнала в эксперименте выбран дискретный случайный сигнал  с корреляционной функцией (28). Выше было показано, что рекуррентные модели со структурой ,  обеспечивают его наилучшую аппроксимацию. Поэтому для анализа эффективности алгоритмов фильтрации и сглаживания в дальнейшем будут использоваться именно указанные модели. Наблюдаемый зашумленный сигнал формировался в соответствии с выражением (29) при отношении сигнал/шум  дБ (, ).

Для исследования алгоритмов фильтрации (36), синтезированных по моделям , , рассчитывались текущие и усредненные по времени среднеквадратические ошибки (СКО) фильтрации ,  по формулам:

        ,              (43)

                               , 

Здесь  – количество реализаций, участвующих в эксперименте, ,  – i-ые отсчеты j-ой реализации сигнала и его фильтрационной оценки, соответственно;  – порядок исследуемой модели, . Относительные ошибки  строились путем нормирования усредненных абсолютных ошибок  к аналогичным ошибкам  (нижней апостериорной границе ошибок), которые соответствуют оптимальным оценкам  фильтра Винера (41) и рассчитывались одновременно с оценками фильтрации. Такая нормировка позволяет оценить потенциальные возможности улучшения качества .

Графики текущих СКО  представлены на рис.5, значения относительных ошибок фильтрации для моделей , , соответственно, равны , , а выигрыш по точности для  составляет .

 

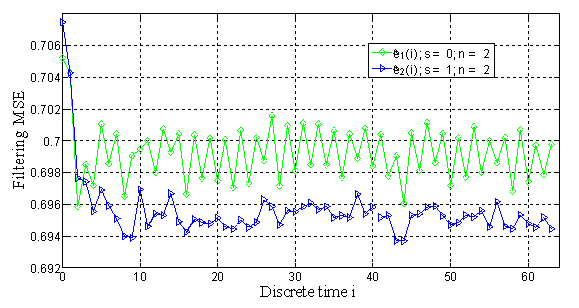
Рис.5.  Ошибки фильтрации для рекуррентных моделей ,  

Анализ кривых рис.5 показывает, что применение модели  позволяет уменьшить не только средний уровень апостериорных ошибок фильтрации, но и их дисперсию (разброс относительно среднего уровня кривой). При этом потенциально обе оценки могут быть улучшены примерно на , если перейти от фильтрации (36) к сглаживанию (41).

Для сравнительного анализа качества оценок сглаживания, получаемых при применении различных аппроксимирующих моделей , ,  воспользуемся алгоритмом (40), полагая, соответственно,  Значения  и  в рекуррентных моделях – те же, что и в задаче фильтрации; корреляционные матрицы  рассчитывались по формулам (22), (23) с использованием соответствующих корреляционных функций . Для получения нижней границы ошибок сглаживания использовался оптимальный нерекуррентный алгоритм Винера (41), построенный для общей стохастической модели  с использованием заданной корреляционной матрицы ,  процесса (1). Имитируемый входной сигнал  и зашумленные наблюдения (29) для всех исследуемых алгоритмов те же, что и в эксперименте фильтрации. Качество сглаживания оценивалось по текущим среднеквадратическим ошибкам:

        ,                         (44)

                               , 

Здесь ,  – i-ые отсчеты j-ой реализации сигнала и оценки сглаживания для соответствующей модели;  и  – те же, что и в эксперименте фильтрации. Кроме того, для модели , используя матрицу  (41), вычислялись теоретические СКО, , которые позволяют судить о состоятельности получаемых оценок. Для указанных моделей рассчитывались также усредненные по времени относительные ошибки фильтрации

                              ,              (45)

Отметим, что одинаковая нормировка у ошибок ,  и один и тот же массив входных реализаций сигнала обеспечивают корректность их сравнения.

Графики всех текущих СКО (44) представлены на рис. 6, значения относительных ошибок сглаживания для моделей  , , соответственно, равны , , , а выигрыш по точности для  по отношению к  составляет . Сравнительный анализ кривых рис. 6 показывает, что применение модели  вместо  позволяет значительно уменьшить ошибки сглаживания. При этом  немного проигрывает нерекуррентной модели  в середине интервала сглаживания, но зато имеет существенно меньшие ошибки сглаживания на его краях, практически приближаясь к теоретическим значениям . По сравнению с фильтром Винера (41), в котором отсутствуют ошибки аппроксимации, проигрыш у моделей  и  оказывается относительно небольшим и составляет , . Однако в рассматриваемой задаче . Поэтому рекуррентная реализация алгоритма сглаживания (39) для модели  по вычислительным затратам может оказаться более предпочтительной, чем нерекуррентная реализация для модели .

 

Рис.6.  Ошибки сглаживания (44) для всех рассматриваемых моделей

 

Литература

1.    С.Л. Марпл-мл. Цифровой спектральный анализ и его приложения. М.: Мир, 1990.

2.    Волчков В.П. Оптимальное рекуррентное представление случайных сигналов в базисах функций Виленкина-Крестенсона.// Радиотехника и электроника, 1997, т. 42, № 8, с. 947-958.

3.    В.П. Волчков, Н.Е. Поборчая. Применение рекуррентных циркулянтных моделей второго порядка для аппроксимации и фильтрации случайных процессов. VI Всероссийская конференция «Радиолокация и радиосвязь», (19-22 ноября) Москва, 2012 г. Сб. докладов, Том.1, с. 105-108.

4.    Хорн Р., Джонсон Ч. Матричный анализ. М.: Мир, 1989.

5.    Волчков В.П. Фидуциальное оценивание m-стационарных гауссовских случайных процессов.// Радиотехника и электроника, 1997, т. 42, № 2, с. 150-160.

6.    Воеводин И.И., Тыртышников Е.Е. Вычислительные процессы с теплицевыми матрицами. М.: Наука, 1987.

7.    В.П. Волчков. Параметрическое спектральное оценивание случайных сигналов с использованием m-рекуррентных моделей. .// Радиотехника и электроника, 1998, т. 43, № 4, с. 421-437.

8.    В.П. Волчков. Фидуциальное оценивание центральной частоты случайного квазигармонического сигнала в базисе дискретных экспоненциальных функций.

9.    Медич Дж. Статистически оптимальные линейные оценки и управление. М: Энергия, 1973.

10. Ахмед Н., Рао К.Р. Ортогональные преобразования при обработке цифровых сигналов. Пер. с англ. Т. Э. Кренкеля. М: Связь, 1980.