УДК 621.382

МОДЕЛИРОВАНИЕ ФИЗИЧЕСКИХ ПРОЦЕССОВ В ПОЛУПРОВОДНИКОВЫХ СТРУКТУРАХ
ПРИ ВОЗДЕЙСТВИИ МОЩНОГО СВЧ-ИМПУЛЬСА. БИПОЛЯРНЫЕ СТРУКТУРЫ

 

С. А. Мещеряков

 

Федеральное автономное учреждение "Государственный научно-исследовательский
испытательный институт проблем технической защиты информации ФСТЭК России"

 

Получена 2 декабря 2013 г.

 

Аннотация. В рамках численной модели в диффузионно-дрейфовом тепловом приближении приведены результаты моделирования физических процессов, протекающих в кремниевой биполярной полупроводниковой структуре при воздействии импульсного сверхвысокочастотного электромагнитного излучения. Представлены энергомощностные и температурные характеристики поведения структуры в широком диапазоне длительностей однократного импульсного воздействия в зависимости от ее конструктивно-технологических параметров.

Ключевые слова: численная модель, диффузия, дрейф, биполярная структура, СВЧ-импульс, тепловое поражение.

Abstract. Results of simulation of the physical processes in silicon bipolar structures at microwave pulse action of electromagnetic radiation are given within the limits of numerical model in drift-diffusion thermodynamic approach. Power and temperature characteristics of structures in durations wide range of the single pulse action depending on their constructive-technological parameters are presented.

Key words: numerical model, diffusion, drift, bipolar structure, microwave pulse, thermal damage.

 

Введение

Представленный в работе [1] подход к расчету энергомощностных и температурных характеристик полупроводниковых структур с барьером Шоттки при воздействии сверхвысокочастотного (СВЧ) импульса электромагнитного излучения (ЭМИ), основанный на решении системы дифференциальных уравнений в диффузионно-дрейфовом тепловом приближении (ДДМТ), позволил дать качественно отличное от [2, 3] описание внутренних взаимосвязанных электро- и теплофизических процессов. Было показано, что рассеиваемая внутри полупроводниковой структуры электрическая мощность преобразуется в Джоулево тепло, связанное с токами проводимости свободных носителей заряда, и термостимулированные генерационно-рекомбинационные процессы. Указанные механизмы приводят не только к выделению тепловой мощности и разогреву структуры, но и к ее частичному поглощению генерационными процессами, что позволяет объяснить рост энергии в области мощных сверхкоротких СВЧ-импульсов и возникновение экспериментально подтвержденного в [4] "генерационного" участка.

Полученные в [1] результаты моделирования показывают, что локализация температуры в ограниченной области структуры с барьером Шоттки, размеры которой определяются, в первую очередь, особенностями внешнего импульсного воздействия и последующего токопереноса, связана с конструктивно-технологическими параметрами структуры. Диоды с барьером Шоттки традиционно считаются униполярными, и, несмотря на то, что в [5] показана необходимость учета при моделировании "жестких" режимов работы обоих типов свободных носителей заряда и полупроводниковой подложки, формирующей изотипный переход с эпитаксиальной пленкой, вклад в общий ток проводимости неосновных носителей заряда незначителен. В отличие от структур с барьером Шоттки механизмы токопереноса в биполярных p – n-переходных структурах базируются, в основном, на поведении неосновных носителей заряда обоих типов, а рекомбинационные процессы в них весьма существенны [6]. Следовательно, можно ожидать определенного различия в энергомощностных характеристиках теплового поражения между биполярными структурами и структурами с барьером Шоттки.

Целью данной работы является моделирование физических процессов в биполярных диодных структурах под воздействием мощного импульсного СВЧ ЭМИ, аналогичное представленному в [1] для барьеров Шоттки.

 

Математическая модель

Как и в [1], будем рассматривать воздействие импульсного СВЧ ЭМИ в виде наведенного на структуру электрического СВЧ-сигнала u(t) с некоторой амплитудой напряжения U₀, пропорциональной мощности импульсного ЭМИ. Результатом воздействия является электрический ток i(t), протекающий внутри диода и поступающий далее в нагрузку тракта обработки сигнала, а возникающий тепловой разогрев, усиливающийся положительной тепловой обратной связью, приводит при импульсном воздействии к повышению температуры внутри структуры. По мере увеличения температуры структура последовательно проходит состояния повышенной рабочей температуры, функциональных сбоев и теплового поражения (выгорания).

Моделирование физических процессов в диодной биполярной структуре проводится, аналогично [1], с использованием системы одномерных дифференциальных уравнений в частных производных в рамках ДДМТ [7, 8]. Система включает уравнение полного тока и два уравнения непрерывности для электронов и дырок, дополненные уравнениями переноса тока и неоднородным уравнением теплопроводности с внутренними источниками и приемниками тепла.

Для решения уравнений задаются следующие граничные и начальные условия. Потенциалы на омических контактах диодной структуры в момент времени t определяются приложенным напряжением u(t). Концентрации свободных носителей заряда на теплоотводящем (температура структуры равна температуре окружающей среды) и на теплоизолированном (градиент температуры нулевой) омических контактах берутся равновесными. Начальным условием являются внутренние распределения поля, концентраций свободных носителей заряда и температуры в диоде при соответствующем режиму эксплуатации постоянном смещении. Электрофизические параметры кремния и их температурные зависимости взяты в соответствии с [9].

 

Результаты моделирования

На рис. 1 представлен профиль распределения легирующей примеси N(x) в кремниевой n⁺– p – p⁺– p⁺⁺ диодной структуре, состоящий из четырех областей: эмиттера с глубиной залегания перехода 1 мкм и уровнем донорного легирования N_d+ = 10¹⁹ см^-3 (в максимуме); базовой области (низколегированной эпитаксиальной пленки) толщиной w_p = 3 мкм и уровнем акцепторного легирования N_a = 10¹⁵ см^-3; высоколегированной акцепторами монокристаллической подложки толщиной w_p+ = 200 мкм и уровнем легирования N_a+ = 5´10¹⁸ см^-3 и области приконтактного акцепторного легирования толщиной w_p++ = 2 мкм и уровнем N_a++ = 10¹⁹ см^-3. К эмиттеру примыкает теплоизолированный омический контакт, к области приконтактного легирования – омический теплоотводящий контакт. Указанные параметры используются по умолчанию, если иное не оговорено. Там же представлены статические вольт-амперные характеристики для данной структуры в прямом и обратном смещении, полученные расчетным путем [1].

  

 

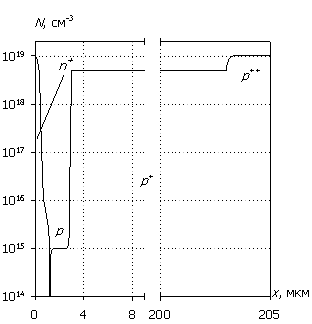
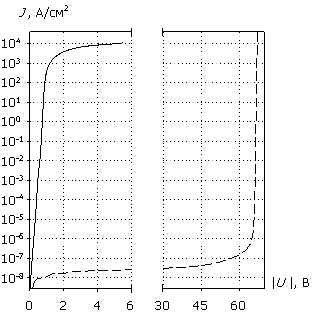
Рис. 1. Профиль легирующей примеси и вольт-амперные характеристики (сплошная линия – прямая, штриховая линия – обратная).

 

Рассмотрим поведение структуры, находящейся при нулевом постоянном смещении, при воздействии на нее импульсного СВЧ ЭМИ с несущей частотой f = 1 ГГц. На рис. 2 приведены зависимости плотности энергии и средней плотности мощности, рассеиваемых в структуре, в зависимости от длительности импульсного СВЧ-воздействия. Характеристики определяются аналогично [1]: интегрирование по длине моделируемой структуры параметров источников и приемников тепла дает мгновенную рассеиваемую плотность мощности P(t); плотность энергии W, рассеиваемая за время импульса t_p, и средняя плотность мощности за время импульса P_mean вычисляются из выражений:

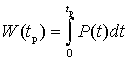,                                                                                      (1)

.                                                                                    (2)

 

Из рис. 2 видно, что, как и в случае структуры с барьером Шоттки [1], характеристика W(t_p) для исследуемой структуры имеет область минимума энергии, приходящуюся в зависимости от температуры саморазогрева T_max на диапазон t_p = 100...1000 нс. Рассмотрим внутренние процессы, протекающие в полупроводниковой структуре и приводящие к данным зависимостям.

 

 

 

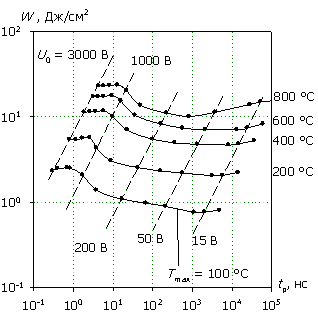
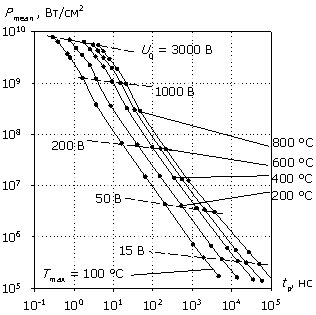
Рис. 2. Зависимости W(t_p) и P_mean(t_p) (в качестве параметров – значения
амплитуды напряжения U₀ воздействующего сигнала и максимальная
температура внутри структуры T_max).

 

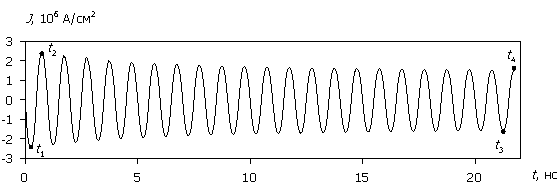
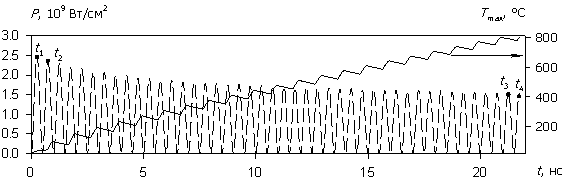
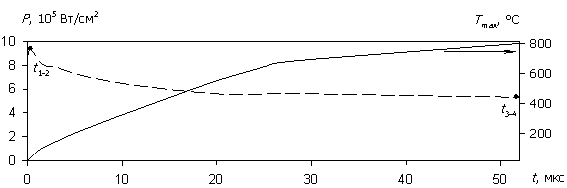
На рис. 3 приведены временные диаграммы плотности тока J(t), протекающего через структуру, рассеиваемой мгновенной плотности мощности P(t) и соответствующей максимальной температуры T_max(t) в моделируемой структуре (для больших временных интервалов на рис. 3в, 3г пунктиром показаны огибающие). Сопоставление зависимостей на рис. 3 показывает, что в отличие от структур с барьером Шоттки, для представленных значений амплитуды напряжения
n⁺– p – p⁺– p⁺⁺ диодная структура изначально пропускает ток в обоих направлениях практически одинаково.

На рис. 4, 5 приведены пространственные распределения внутренних характеристик, соответствующие отмеченным временным точкам на рис. 3а, 3б. Аналогично [1], n⁺– p – p⁺– p⁺⁺ диодная структура при амплитуде входного сигнала U₀ = 1000 В находится в режиме существенной модуляции проводимости базовой области, как в прямом, так и в обратном смещении. Данный режим поддерживается при прямой полуволне воздействующего сигнала инжекцией носителей из высоколегированной подложки, а при обратной полуволне – ударной ионизацией. Максимальная рассеиваемая мощность локализуется у теплоизолированного контакта и в области изотипного p⁺– p⁺⁺-перехода, и там же происходит наибольший рост температуры.

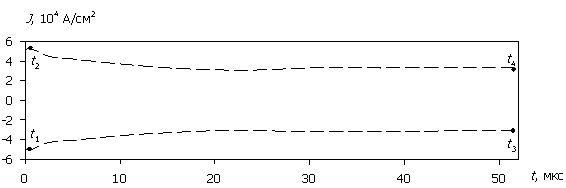
При относительно малых амплитудах воздействующих сигналов ситуация иная, но в отличие от диодов Шоттки, принципиальная разница между режимами видна только при рассмотрении "внутренних" характеристик. На рис. 6, 7 приведены пространственные распределения ряда характеристик, соответствующие отмеченным временным точкам на рис. 3в, 3г при амплитуде воздействующего напряжения U₀ = 15 В. В этом режиме напряженности электрического поля изначально недостаточно для ударной ионизации, способной обеспечить режим лавинной генерации носителей. В результате этого возникает постепенная "накачка" носителей заряда за счет процессов инжекции на прямой полуволне сигнала в базовую область и медленный рост температуры с относительно равномерным разогревом всей структуры.

 

(а)

(б)

(в)

(г)

 

Рис. 3. Зависимости J(t), P(t) и T_max(t) при различных значениях амплитуды напряжения U₀ воздействующего СВЧ-сигнала.
(а), (б) – U₀ = 1000 В; (в), (г) – U₀ = 15 В.

 

 

   

 

   

 

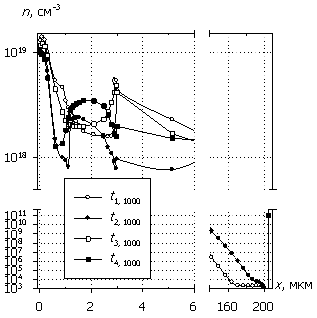
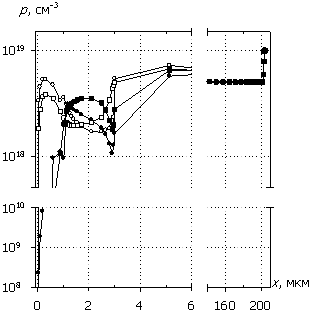
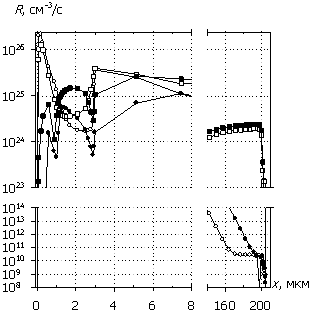
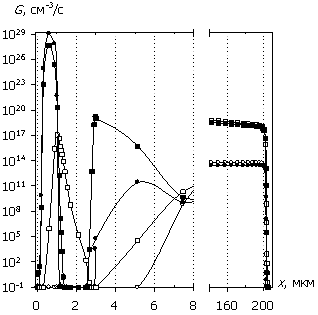
Рис. 4. Распределения электронов n(x), дырок p(x), темпа рекомбинации R(x) и
темпа генерации G(x); U₀ = 1000 В. Маркеры кривых соответствуют n(x).

 

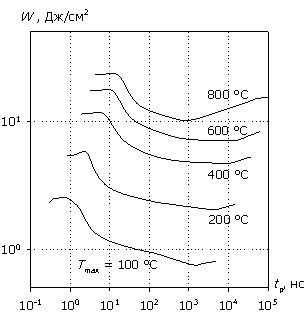
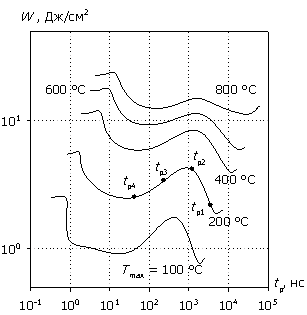
На рис. 8а, 8б представлена характеристика W(t_p) для двух толщин эпитаксиальной пленки, являющейся основой базовой области диодной структуры, демонстрирующая, что при увеличении толщины эпитаксиальной пленки, и, следовательно, базовой области диодной структуры, наблюдается существенное искажение энергетических характеристик с некоторым увеличением их абсолютных значений во всем интервале исследуемых температур саморазогрева. При этом в диапазоне 100 нс…10 мкс возникает участок с достаточно большим максимумом энергии, связанный с поведением темпа рекомбинации внутри структуры. С уменьшением длительности импульсного воздействия (при одновременном увеличении воздействующей мощности) увеличивается количество избыточных свободных носителей заряда в низколегированной области

 

 

    

 

    

 

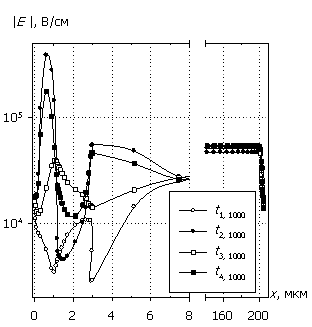
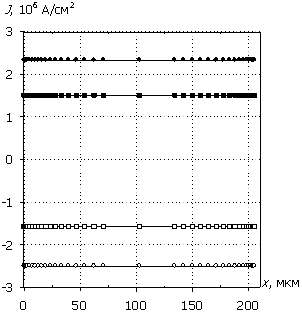
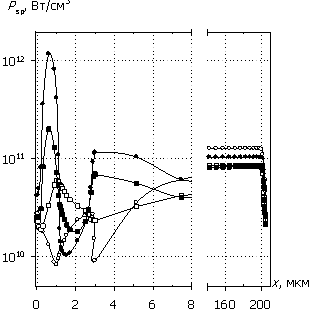
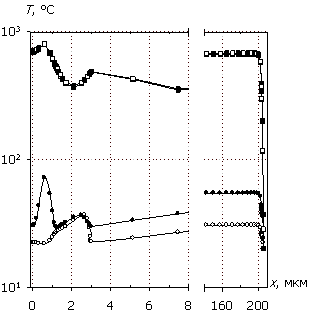
Рис. 5. Распределения электрического поля E(x), плотности тока J(x), удельной электрической мощности P_sp(x) и температуры T(x); U₀ = 1000 В.
Маркеры кривых соответствуют E(x).

 

   

 

    

 

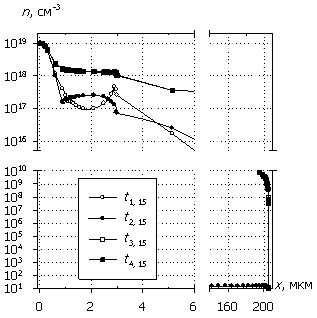
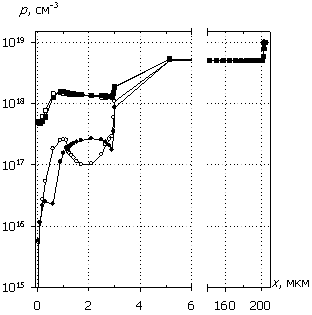
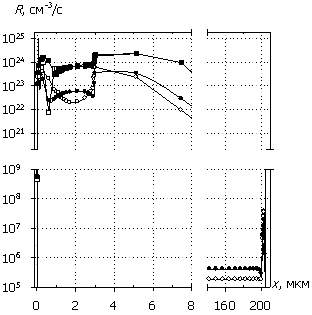
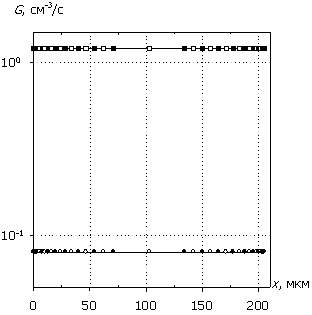
Рис. 6. Распределения электронов n(x), дырок p(x), темпа рекомбинации R(x) и
темпа генерации G(x); U₀ = 15 В. Маркеры кривых соответствуют n(x).

 

базы, концентрация которых затем экспоненциально спадает в достаточно протяженной подложке. Соответственно, чем толще база (при прочих равных условиях), тем больше заряда в ней будет накоплено, и тем выше окажется концентрация свободных носителей в области подложки. Данный процесс усугубляется ограничением области подложки двумя изотипными переходами p – p⁺ и
p⁺– p⁺⁺, ограничивающими скорость оттока неравновесных носителей через близлежащие омические контакты. Это влечет за собой усиление рекомбинационных процессов в области подложки, неравномерно распределенных в ней и дающих дополнительный вклад в саморазогрев структуры, что отражается на ее энергомощностных характеристиках.

 

     

 

    

 

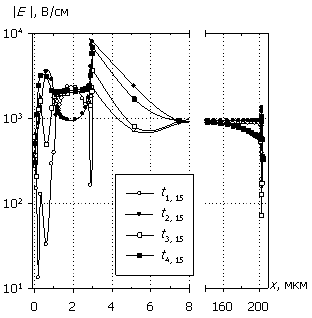
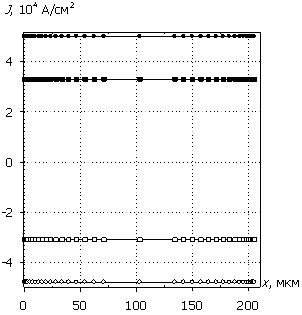
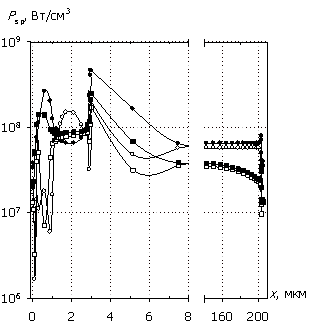
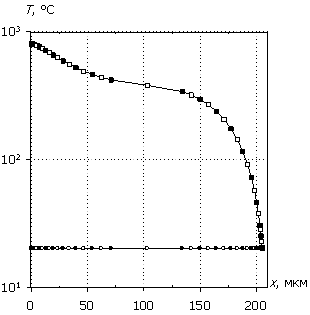
Рис. 7. Распределения электрического поля E(x), плотности тока J(x),
рассеиваемой удельной мощности P_sp(x) и температуры T(x); U₀ = 15 В.
Маркеры кривых соответствуют E(x).

 

 

     

(а)                                                                            (б)

Рис. 8. Зависимость W(t_p) для различных значений толщины эпитаксиальной пленки w_p: (а) – 3мкм; (б) – 10 мкм.

 

Рис. 9 показывает, что с увеличением уровня воздействующего сигнала и уменьшением его длительности большая часть рассеиваемой в диодной структуре мощности перераспределяется из области низколегированной базы в область высоколегированной подложки. Приведенное в таблице 1 рассчитанное значение дисперсии характеристики Р/P_max(x) имеет точку минимума (выделено цветом) для t_p2, соответствующую максимуму энергии на рис. 8б. Иными словами, равномерно распределенная по всей структуре мощность в отсутствии существенных генерационных процессов при средних значениях амплитуды воздействующего сигнала дает максимальную величину энергии саморазогрева. Данная ситуация будет нивелироваться с уменьшением толщины базы при фиксированной частоте сигнала и усиливаться с увеличением частоты при фиксированной толщине базы.

Расчеты показывают, что характеристики W(t_p), аналогично структуре с барьером Шоттки в [1], практически не зависят от степени легирования эпитаксиальной пленки из-за высокого уровня инжекции свободных носителей заряда и сильной модуляции проводимости низколегированной базовой области в процессе импульсного воздействия.

 

    

 

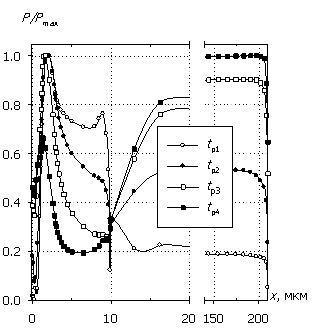
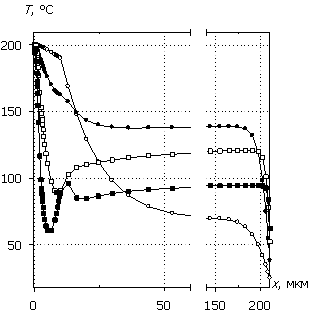
Рис. 9. Распределения P/P_max(x) и T(x) для различных импульсных воздействий.
Приведенные кривые соответствуют точкам на рис. 8(б).

 

 

Таблица 1. Оценка равномерности распределения мощности

Обозначение	Длительность импульса tp, нс	Амплитуда импульса U0, В	Плотность рассеиваемой энергии W, Дж/см2	Средняя плотность рассеиваемой мощности Рmean, Вт/см2	Дисперсия зависимости Р/Pmax(x)
tp1	3570	20	2.18	6.11×105	0.10
tp2	1207	50	4.18	3.50×106	0.05
tp3	235	100	3.40	1.45×107	0.06
tp4	43	200	2.53	5.90×107	0.08

 

Заключение

Полученные в рамках данной работы результаты численного моделирования показывают, что механизмы, приводящие к тепловому разогреву биполярной структуры и структуры с барьером Шоттки [1], одинаковы. Однако влияние рекомбинации на протекающие электротепловые процессы для биполярной структуры более существенно, чем для структур с барьером Шоттки, что отражается на "внешних" характеристиках биполярной структуры (плотности тока и, как следствие, мощности), поведение которых схоже (с точностью до тенденций) и при очень больших, и при относительно малых амплитудах напряжения наведенного импульсным ЭМИ сигнала.

Являясь согласно модели ДДМТ дополнительным источником тепла, рекомбинация, с одной стороны, "выравнивает" рассеиваемую тепловую энергию по длине структуры в широком диапазоне амплитуд воздействующего импульса. С другой стороны, поведение рекомбинационных процессов при длительностях импульса 200…2000 нс (в зависимости от T_max) приводит к возникновению специфического максимума на энергетической характеристике W(t_p). При f = 1 ГГц указанный максимум наиболее выражен для биполярных структур с толстой базой. Для структур с тонкой базой аналогичный эффект будет наблюдаться при увеличении частоты воздействующего сигнала.

На зависимости W(t_p) для n⁺– p – p⁺– p⁺⁺ структуры можно выделить известные согласно классическим тепловым моделям [2, 3] характерные участки, а также генерационный участок, описанный в [1, 4], и соответствующий росту энергии, необходимой для разогрева при длительностях воздействующего
СВЧ-импульса менее 100 нс.

 

Литература

1.            С.А. Мещеряков.  Моделирование физических процессов в полупроводниковых структурах при воздействии мощного СВЧ-импульса. Структуры с барьером Шоттки. // Журнал радиоэлектроники: электронный журнал. 2013. № 11. URL: http://jre.cplire.ru/jre/nov13/2/text.pdf

2.            D.M. Taska.  Pulse power failure modes in semiconductors // IEEE Trans. 1970. V. NS-17. P. 364–372.

3.            V.M. Dwyer, A.J. Franklin, D.S. Campbell.  Thermal failure in semiconductor devices // Solid-State Electron. 1990. V.33. P. 553–560.

4.            Ю.Г. Юшков, П.Ю. Чумерин, С.Н. Артеменко и др.  Экспериментальное исследование воздействия сверхвысокочастотных импульсов на работу персонального компьютера // Радиотехника и электроника. 2001. Т. 46. №8. С. 1020–1024.

5.            A.I. Prokopyev, S.A. Mesheryakov.  Static characteristics of high-barrier Schottky diode under high level injection // Solid-State Electron. 1999. V 43. N 9. P. 1747–1753.

6.            Зи С. Физика полупроводниковых приборов. М.: Мир, 1984. Кн. 1. 456 с.

7.            G.K. Wachutka.  Rigorous thermodynamic treatment of heat generation and conduction in semiconductor device modeling// IEEE Trans. 1990. V. CAD-9. P. 1141–1149.

8.            Мещеряков С.А., Бердышев А.В.  Электротепловая модель воздействия электромагнитного излучения на полупроводниковые структуры // Радиотехника и электроника. 2013. Т. 58. № 11. С. 1127–1135.

9.            NSM Archive – Physical Properties of Semiconductors // [Электронный ресурс]. URL: http://www.ioffe.rssi.ru\SVA\NSM\Semicond\index.html