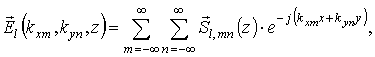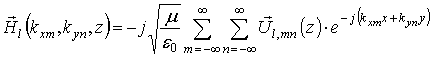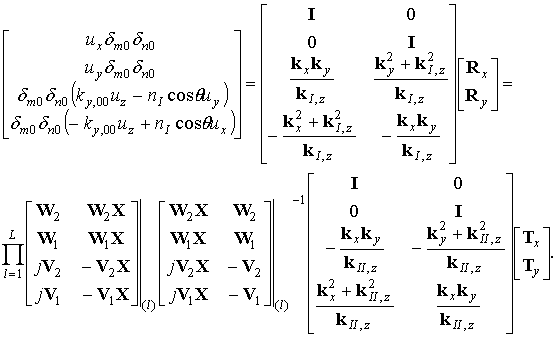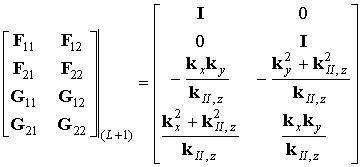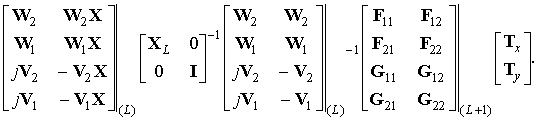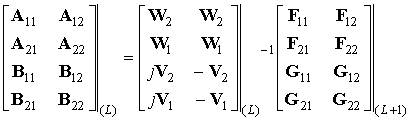УДК 001.891.573
3D МОДЕЛИРОВАНИЕ ЭЛЕКТРОМАГНИТНОГО РАССЕЯНИЯ НА РПМ МЕТОДОМ СВЯЗАННЫХ ВОЛН
А. В. Никитенко 1,2, А. С. Зубов 2, Е. В. Булычев 2
1 МГУ имени М.В. Ломоносова, физический факультет, Москва
2 ИТПЭ РАН
Статья получена 8 декабря 2014 г.
Аннотация. Рассматривается возможность применения метода связанных волн (RCWA) к задаче расчета отражения электромагнитных волн от двухпериодического радиопоглощающего материала. Основной задачей исследования была оценка эффективности данного метода для расчета материалов, использующихся для покрытия стен безэховых камер, и для включения этого алгоритма расчета в комплекс программ по оптимизации компактных полигонов. Использованы различные модификации метода, выбран способ формирования ключевых матриц алгоритма и решения конечной системы уравнений, возникающей в процессе реализации алгоритма. Исследована сходимость алгоритма, проведено сравнение результатов с другими методами решения подобных задач, в частности, методом конечных элементов и методом моментов, реализованных в коммерческих пакетах программ. Сравнение проводилось по таким параметрам, как: точность решения, скорость счета, скорость сходимости. Сравнение проведено на примере расчета материала с параметрами, аналогичными коммерческому пирамидальному материалу, уже имеющему широкое применение на практике. Показано, что метод является достаточно эффективным и по многим параметрам выигрывает у других методов расчета, особенно при расчете материалов с неоднородной диэлектрической проницаемостью и/или материалов, покрытых согласующими слоями.
Ключевые слова: метод связанных волн, радиопоглощающий материал, безэховая камера, компактный полигон.
Abstract. The three-dimensional RCWA method applied to the scattering problem for a two-dimensional radio-absorbing material is presented. The goal of this study is to check applicability of the method for calculation of reflection indices of materials used in modern unechoic chambers and compact ranges. The RCWA method is considered with some enhancements, in particular: method of an eigenvalue problem forming is presented, method of solving final system of linear equations is chosen. Calculations are conducted using characteristics of a commercial pyramidal radio-absorbing material. Verification of the results conducted by RCWA is presented by comparison with results obtained by two different methods –the finite element method and moment method. Good agreement in both cases is shown. Also, it is shown that 3D RCWA algorithm’s performance is at least not worse than others; furthermore 3D RCWA algorithm appears to be better at calculating diffraction on layered materials with non-homogeneous permittivity.
Key words: 3D RCWA, radio-absorbing material, unechoic chamber, compact range.
Введение
Современная электроника, антенны, входящие в состав комплексов связи и прочие устройства на различных этапах своего создания проходят множество тестов и экспериментальных исследований, например, измерения электромагнитных параметров и тесты на электромагнитную совместимость. Измерения электромагнитных свойств проводят как на открытой местности, так и в закрытых помещениях, называемых компактными полигонами [1].
Компактный полигон представляет собой безэховую камеру (помещение, стены которого покрыты радиопоглощающим материалом) и установленный внутри коллиматор для создания поля в рабочей зоне, куда помещается объект измерений. Современные требования к точности измерений на таких полигонах очень высоки, как, соответственно, и требования к характеристикам самих камер, в частности, к степени неравномерности поля в рабочей зоне.
Одним из важных факторов, влияющих на неравномерность поля, является отражение электромагнитных волн от поглощающего материала, которым покрыты стенки БЭК. Существенный вклад в неравномерность также вносит поле, излученное облучателем, отраженное от пола БЭК, и затем переотраженное от зеркала коллиматора. Таким образом, расчет электромагнитных характеристик радиопоглощающих материалов, использующихся в безэховых камерах, имеет большую практическую значимость. Данные таких расчетов могут быть использованы для высокоточного моделирования электромагнитного поля в рабочей зоне компактных полигонов, в задачах оптимизации конфигурации безэховых камер, в задачах синтеза радиопоглощающих материалов с заданной формой и свойствами.
Радиопоглощающие материалы являются, как правило, периодическими структурами. В практике встречаются однопериодические материалы – чаще всего клиновидной формы, и двухпериодические, например, пирамидальной формы. Особый интерес представляют материалы с неоднородными электромагнитными свойствами. Это могут быть материалы с покрытием из тонких слоев с различными значениями диэлектрической проницаемости, материалы с плавным изменением диэлектрической проницаемости по направлению от поверхности материала вглубь и другие.
В исследуемом диапазоне частот соотношение длины падающей волны и размеров радиопоглощающих материалов, использующихся в безэховых камерах, таково, что уровень дифракционных лепестков может превышать уровень зеркально отраженной волны [2]. Спецификации фирм – производителей РПМ обычно описывают частотно-угловые зависимости лишь для зеркального отражения. Полный учет отражения во всех направлениях позволяет более точно сформулировать требования к радиопоглощающему материалу при создании новой камеры или усовершенствовании старой.
Для численного решения задач дифракции в электродинамике используются различные подходы, такие как метод конечных разностей, метод конечных элементов, метод моментов, Фурье-методы и другие. В данной работе рассматривается применение метода связанных волн, вместе с некоторыми модификациями, к задаче расчета отражения от РПМ. Существуют различные варианты как формулировки, так и непосредственной реализации этого метода, примеры можно найти в работах [3-6]. Авторами были изучены достоинства и недостатки различных подходов и модификаций метода, связанных с формированием системы уравнений на собственные значения и с алгоритмом решения конечной системы линейных уравнений. В соответствие с требованиями к скорости и точности расчета были выбраны и улучшены необходимые модификации. Проводится сравнение эффективности метода с двумя традиционными методами решения – методом конечных элементов и методом моментов. Сравниваются важные характеристики методов – сходимость, время счета, точность расчетов.
Сравнение методов произведено на основе расчета отражательных характеристик пирамидального радиопоглощающего материала, широко использующегося для покрытия стен реальных безэховых камер,
1. Постановка задачи
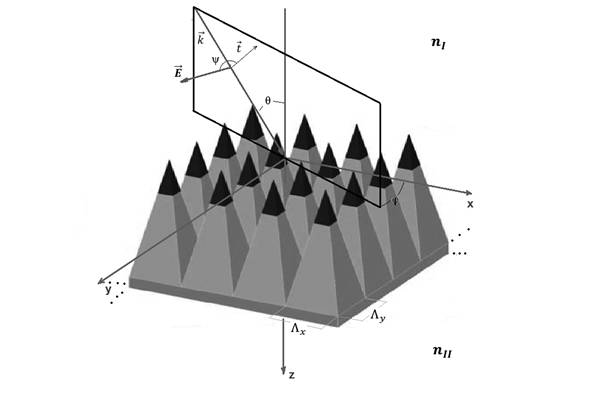
Рис. 1. Геометрия задачи.
Рассматривается
отражение плоской электромагнитной волны от радиопоглощающего материала, угол
падения и поляризация произвольные. Материал представляет собой бесконечную
периодическую пирамидальную структуру с электромагнитными характеристиками µ=1
и 
на заданной частоте (см. рис. 1) , все
пирамидки установлены на слой-подложку из такого же материала. Полупространство
над материалом заполнено однородной средой с коэффициентом преломления 
, полупространство под материалом
заполнено однородной средой с коэффициентом преломления 
.
Период структуры материала не превышает десяти длин волн, высота не превышает
тридцати длин волн, модуль коэффициента преломления материала 
.
Введем
декартову систему координат, как показано на рис. 1 . Оси X и Y
направим параллельно перпендикулярным сторонам оснований пирамид. Начало
координат разместим на вершине одной из пирамид. Ось Z направим
перпендикулярно плоскости основания материала, вниз. Период структуры материала
вдоль оси X обозначим 
, вдоль оси Y - 
.
Плоскость, содержащая волновой вектор k и ось Z, образует угол φ с осью X, вектор k направлен под углом Θ к оси Z, а вектор электрической напряженности поля образует угол ψ с плоскостью падения.
2. Метод связанных волн для случая произвольного падения плоской волны
Напомним основные идеи метода связанных волн (аналогичное изложение для однопериодической структуры можно найти в работах [7, 8, 9]. Поле в верхнем полупространстве представляет собой сумму поля падающей плоской волны и поля отраженной волны, которое можно разложить в ряд по плоским волнам (гармоникам). Таким образом, поле в верхнем полупространстве представляется в виде суперпозиции плоских волн, у каждой из которых свое значение амплитуды. Разобьем радиопоглощающий материал на достаточно тонкие слои. Поле в каждом слое представляется в виде ряда Рэлея-Флоке [10]. Функция диэлектрической проницаемости в каждом слое раскладывается в ряд Фурье. Подставляя эти ряды в уравнения Максвелла и проводя необходимые преобразования, получаем систему линейных уравнений. Искомые поля раскладываются в ряд по собственным векторам матрицы этой системы, а коэффициенты этих разложений и являются амплитудами отраженных и прошедших гармоник. Чтобы найти эти коэффициенты, используют условия сопряжения на границе раздела двух соседних слоев, а именно, условия равенства тангенциальных составляющих полей.
Рассмотрим алгоритм решения подробнее. Для удобства будем использовать обозначения, принятые в статье [9].
Для падающей волны можно записать:
,
где
, 
–
модуль волнового вектора падающей волны, j - мнимая единица, здесь и в
дальнейших выкладках зависимость от времени 
опущена.
Для поля в верхнем (I) и нижнем (II) полупространствах имеем:
где 
и 
-
искомые коэффициенты разложения, D – высота материала, а
коэффициенты 
определяются из соотношений согласования
фаз и условий Флоке [11]:
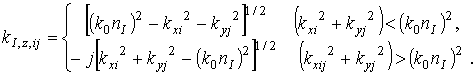
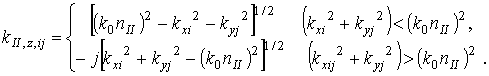
Разложим
электрическую 
и магнитную 
составляющие поля в слое l
в ряд Фурье:
Подставим полученные представления (2) и (3) в уравнения Максвелла
и выразим z компоненты поля через x и y компоненты. Воспользуемся тем фактом, что если некоторая периодическая функция представляет собой произведение двух других периодических функций:
то эта функция может быть разложена в ряд:
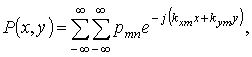
причем коэффициенты
разложения 
выражаются через свертку коэффициентов
Фурье fi и gj функций 
и 
соответственно:
С помощью выражения (*) можно записать в виде ряда произведение функции диэлектрической проницаемости (или обратной ей величины) и одной из компонент поля. Какая именно величина - сама диэлектрическая проницаемость или обратная ей величина – участвует в разложении – зависит от вида уравнения до разложения в ряды. Выбор вида уравнений и, соответственно, величин, участвующих в разложении в ряды, влияет на скорость сходимости конечного результата [12]. В данной работе предложены следующие уравнения (вид этих соотношений не зависит от номера слоя, поэтому индекс l опущен):
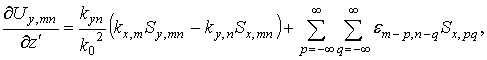
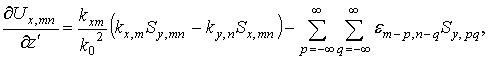
где 
, 
-
коэффициенты ряда Фурье для диэлектрической проницаемости, 
- коэффициенты ряда Фурье для величины,
обратной диэлектрической проницаемости. Для численного решения этой системы
необходимо оставить конечное число членов в каждой двойной сумме. Такую
конечную систему можно, проведя соответствующие преобразования, представить в
матричной форме:
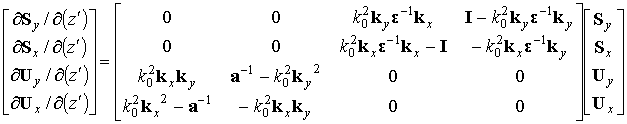
где I
– единичная матрица,
и 
-
диагональные матрицы с элементами на главной диагонали 
и
соответственно,
–
матрица, составленная из коэффициентов ряда Фурье для диэлектрической
проницаемости,
– матрица, составленная
коэффициентов ряда Фурье для величины, обратной диэлектрической проницаемости.
С помощью вторых производных компонент поля, можно получить эти уравнения в более компактном виде:
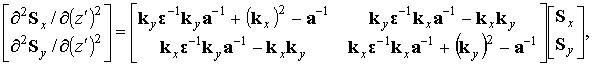
Введем следующие обозначения:
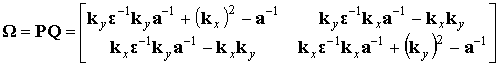
Полученная
система однородных дифференциальных уравнений решается путем нахождения
собственных векторов и собственных значений матрицы 
.
Обозначим диагональную матрицу корней из найденных собственных значений 
, а
матрицу, составленную из собственных векторов, разобьем на две матрицы
следующим образом:
Разложим
тангенциальные компоненты 
в ряд по найденным
собственным векторам:
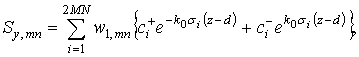
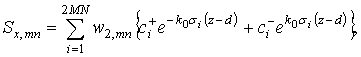
где 
и 
–
элементы матриц 
и соответственно,
d – толщина одного слоя. Аналогичные выражения можно
записать для 
. Эти соотношения можно записать в
матричной форме для электрической и магнитной составляющих поля:
(4.2)
(4.3)
(4.4)
где 
- матрицы коэффициентов разложения, 
– диагональная матрица с элементами на
главной диагонали, равными 
, матрицы 
определяются следующими соотношениями:
Запишем условия сопряжения на границе раздела двух соседних слоев – условия непрерывности тангенциальных компонент поля:
Подставляя в эти соотношения выражения (2), (3), (4.1 - 4.4), получаем уравнения на верхней границе (между верхним полупространством и первым слоем):
Аналогичное выражение можно записать для границы раздела каждого из l-ого и l+1-ого слоев:
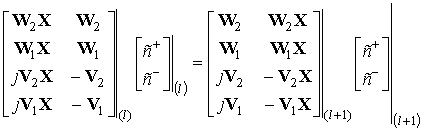
На границе между нижним полупространством и материалом получаем уравнения в следующем виде:
где L – число слоев, на которые разбит материал.
Избавляясь
от коэффициентов 
, получаем систему уравнений для
нахождения искомых амплитуд:
3. Метод улучшенной матрицы прохождения
Расчет
коэффициентов системы (5) включает L обращений составных матриц. Эти
матрицы содержат в себе матрицы с экспонентами от
собственных значений на главной диагонали. В наборе собственных значений есть
величины с большой вещественной частью. Поэтому матрицы будут
содержать столбцы значений, близких к нулю, что может привести к ошибкам при
обращении составной матрицы. Наиболее важно это для материалов с большим
значением мнимой части диэлектрической проницаемости, как, например, в
материале, представляющем интерес в данной работе. Обобщим метод улучшенной
матрицы прохождения из работы [11] для двухпериодической структуры.
Поэтому прежде, чем решать систему, преобразуем ее к виду, не требующему обращения вышеуказанных матриц. Для начала, введем следующие обозначения:
Тогда последний множитель в произведении (5) можно представить в таком виде:
Введем следующие обозначения:
Рассмотрим замену:
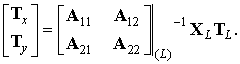
Введем дополнительные обозначения:
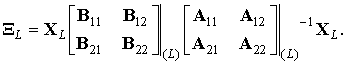
Совершая подстановку (7) и (8) в (6), получаем следующее выражение для матриц F, G на L-том слое:
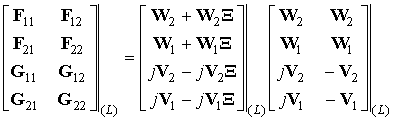
Таким образом, мы, не обращая матрицу экспонент от собственных значений, представили предпоследний множитель произведения в виде, аналогичном (7). Этот процесс можно повторить по всем слоям, и в итоге получить систему уравнений следующего вида:
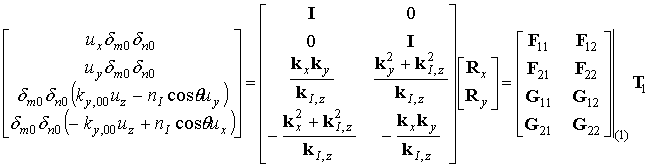
Эта система уравнений может быть решена численно с помощью стандартного LU-разложения без численной нестабильности.
4. Сходимость и верификация алгоритма. Результаты расчетов
В работах по методу связанных волн верификация проводится различными способами: проверяется закон сохранения энергии для периодической структуры без поглощения, исследуется сходимость полной рассеянной энергии в зависимости от количества гармоник, учтенных при расчете, сравниваются результаты расчетов с аналогичными из других статей. Сами объекты сравнения при этом достаточно просты, зачастую состоят из немногих (меньше десяти) слоев.
В данной работе требуемая точность расчетов радиопоглощающего материала достаточно высока ~0.3 дБ. Поскольку при расчете поля в рабочей зоне безэховой камеры вклады гармоник могут быть проанализированы отдельно, возникает потребность анализировать сходимости гармоник по-отдельности, а не рассматривать сходимость полной рассеянной энергии. Кроме того, в методе используется еще одно приближение – ступенчатая аппроксимация геометрической формы материала. Таким образом, должна быть исследована сходимость амплитуд отраженных гармоник в зависимости от числа слоев, на которые разбивается материал.
Также отдельной особенностью исследуемого материала является особенно низкий уровень амплитуды отраженной волны.
Поэтому была проведена верификация алгоритма путем расчета тестового материала другими методами, а именно методом моментов и методом конечных элементов.
Во
всех расчетах, приведенных ниже, а именно, в сравнении результатов алгоритмов,
графиках сходимости и результатах расчета пирамидального материала нижнее
полупространство 
заполнено металлом.
Для сравнения был использован материал пирамидальной формы, аналогичный используемому в реальных безэховых камерах. Высота пирамид (без подложки-основания) 25.1 см, толщина подложки-основания – 2.7 см, период по обеим осям – 10.2 см. В отличие от реальных материалов, обладающих дисперсией, диэлектрическая проницаемость полагается константой, равной 2.248-1.751i , магнитная проницаемость равна 1. Расчеты методом моментов выполнены с помощью программы FEKO, расчеты методом конечных элементов выполнены с помощью программы HFSS, алгоритм RCWA реализован в виде программы на языке C++ с использованием библиотек MKL (Intel Math Kernel Library). Результаты расчетов нулевой гармоники представлены на рис. 2.
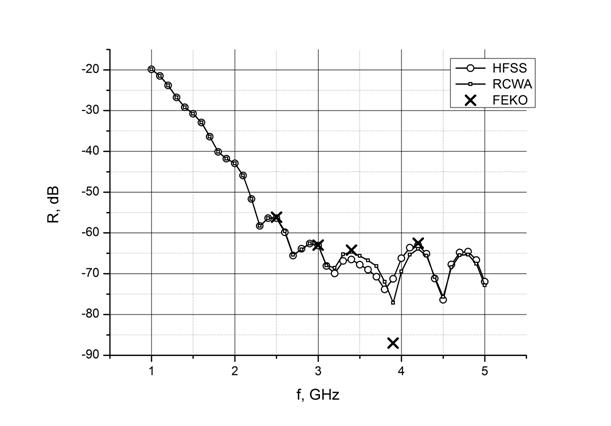
Рис. 2. Графики зависимости амплитуды главной (0,0) гармоники от частоты.
Расчет одной точки методом моментов на программе FEKO на специальном расчетном кластере (96 ядер) занимает очень большое время – десятки часов, поэтому результаты были получены в отдельных точках. Расчеты методом конечных элементов и методом связанных волн имеют одинаковый порядок по скорости счета – десять минут на точку. В среднем, программа HFSS, запущенная на компьютере с 6-ти ядерным процессором, выполняет расчет немного быстрее. Однако на рисунке можно заметить участок (3.2 ГГц – 5.0 ГГц), в котором результаты заметно расходятся. На этом участке не удалось добиться сходимости метода конечных элементов с необходимой точностью, так как для расчетов потребовалось более 8 ГБ оперативной памяти. На этом участке достигается значительный минимум по амплитуде, поэтому точность должна быть еще выше. По-видимому, этим же объясняется столь значительное расхождение с FEKO на частоте 3.9 ГГц.
Также исследована сходимость алгоритма метода связанных волн в зависимости от числа сохраненных гармоник и в зависимости от числа слоев. Расчет проводился для реального коммерческого материала пирамидальной формы. Высота пирамид (без подложки-основания) 27.8 см, толщина подложки-основания – 2.7 см, период по обеим осям – 10.2 см. Магнитная проницаемость равна 1. Зависимость диэлектрической проницаемости от частоты показана на рис. 3.
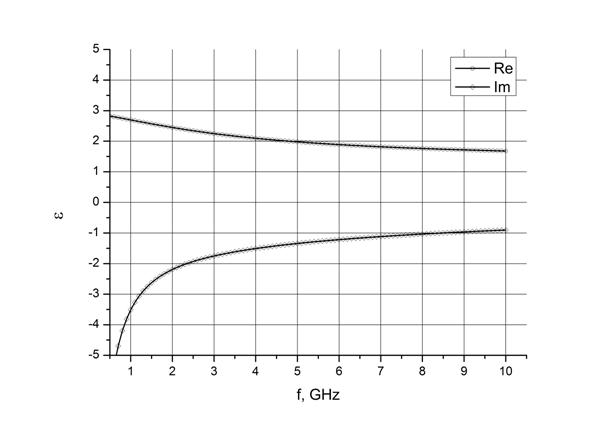
Рис. 3. График зависимости действительной и мнимой части диэлектрической проницаемости радиопоглощающего материала, использовавшегося в расчетах, от частоты.
Напомним, что при реализации метода связанных волн используется приближения в виде ступенчатой аппроксимации профиля материала и замены бесконечной суммы гармоник на конечную. Поэтому перед началом расчетов был проведен выбор количества слоев и количества гармоник, необходимых для достижения точности в расчете амплитуды ~0.3 дБ. Расчеты для осуществления такого выбора были проведены на частотах 3 ГГц (так как примерно на этой частоте при нормальном падении появляются побочные гармоники) и на частоте 8 ГГц. Все расчеты выполнены для угла ψ=90°, так как в этом случае, как правило, при наклонном падении отражение от материала больше, чем при других значениях углов.
Были рассмотрены как случай нормального падения, так и случай падения под скользящим углом. На рис. 4 представлены графики сходимости амплитуды гармоник в зависимости от общего числа гармоник, учтенных при расчете в случае нормального падения. Необходимая точность достигается при учете по 17 гармоник по обеим осям. На этом и последующих графиках гармоники обозначены их индексами Флоке (например, главная гармоника обозначается (0,0)). На аналогичном графике при наклонном падении (рис. 5) видно, что достаточно учесть всего по 13 гармоник по обеим осям. На частоте 8 ГГц при наклонном падении (рис. 6) ситуация ухудшается – если для главной гармоники достаточно 13 гармоник по обеим осям, то для побочной гармоники, которая появляется на этой частоте, уже необходимо учесть в расчете 21 гармонику по обеим осям.
На рис. 7, 8 представлены графики сходимости в зависимости от количества слоев, на которые разбивается материал. На рис. 7 представлены расчеты на разных частотах при нормальном падении, на рис. 8 – при падении под углами θ=80°, φ=45°. При скользящих углах падения достаточно малого количества слоев – требуемая точность достигается и в главной, и в побочных гармониках уже при расчете с 50 слоями (100 слоями на 8 ГГц). Для нормального падения ситуация хуже, и для получения результата с заданной точностью на всем рассматриваемом диапазоне частот необходимо разбиение в 300 слоев.
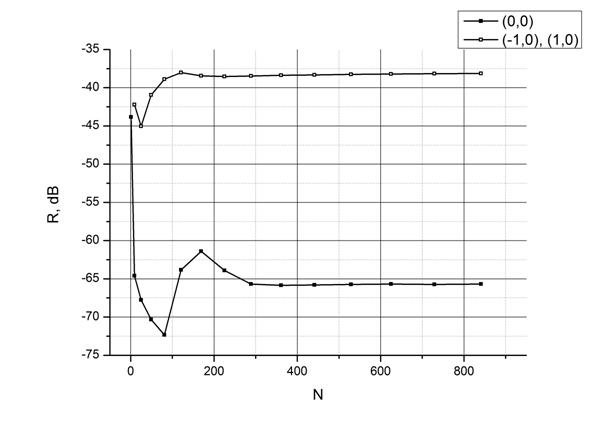
Рис. 4. Сходимость главной и побочных гармоник в зависимости от количества учтенных при расчете гармоник, θ=0°, φ=0°, ψ=90°,частота 3 ГГц.
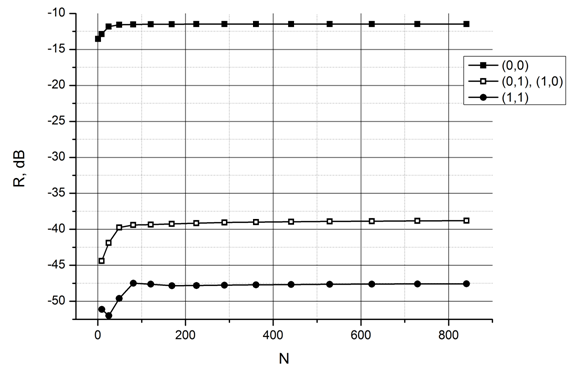
Рис. 5. Сходимость главной и побочных гармоник в зависимости от количества учтенных при расчете гармоник, θ=80°, φ=45°, ψ=90°, частота 3 ГГц.
Рис. 6. Сходимость главной и побочных
гармоник в зависимости от количества учтенных при расчете гармоник, θ=80°,
φ=45°, ψ=90°, частота 8 ГГц.
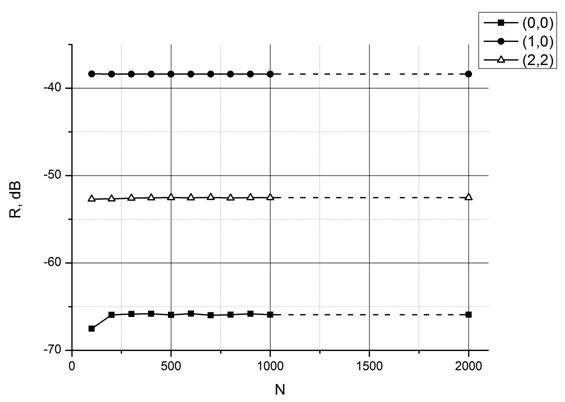
Рис. 7. Сходимость главной и побочных гармоник в зависимости от количества слоев, на которые разбивается материал, θ=0°, φ=0°, ψ=90°,черные символы - частота 3 ГГц, белые – 8 ГГц.
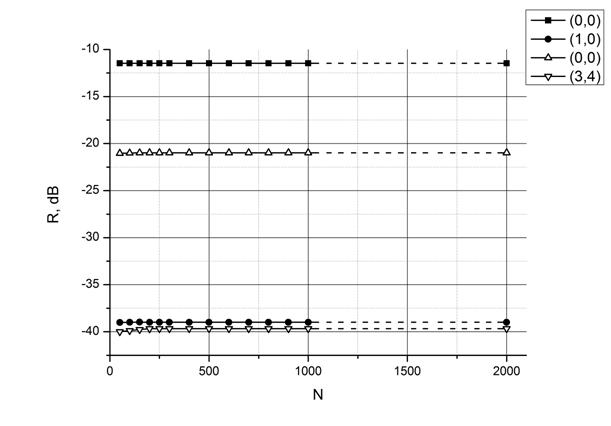
Рис. 8. Сходимость главной и побочных гармоник в зависимости от количества слоев, на которые разбивается материал, θ=80°, φ=45°, ψ=90°,черные символы - частота 3 ГГц, белые – 8 ГГц.
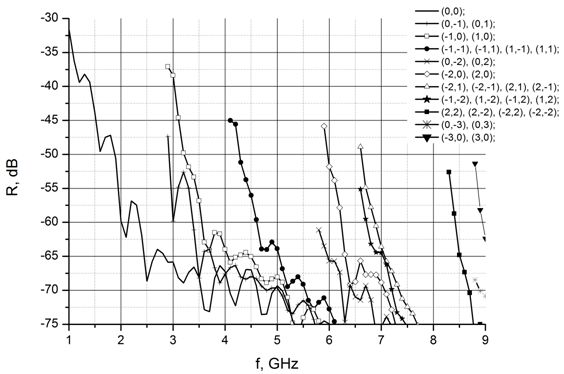
Рис. 9. Результаты расчета пирамидального материала. Углы падения: φ=0°, θ=0°, ψ=90°.
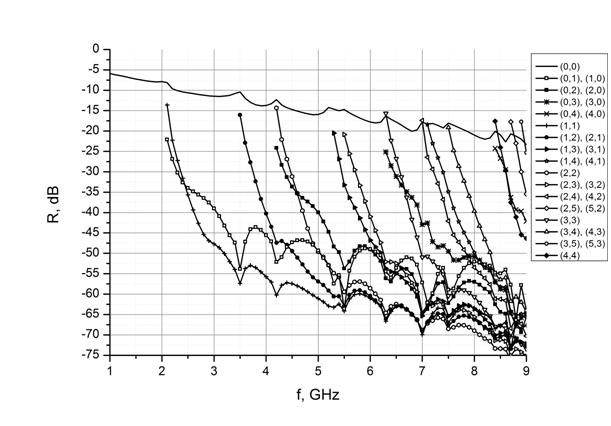
Рис. 10. Результаты расчета пирамидального материала. Углы падения: φ=45°, θ=80°, ψ=90°.
На рисунках 9, 10 представлены результаты расчетов коммерческого пирамидального радиопоглощающего материала в виде графиков зависимостей амплитуды каждой гармоники от частоты. Нескольким гармоникам может соответствовать одна линия, если ввиду симметрии эти гармоники совпадают. Видно, что на многих частотах уровень отраженных побочных гармоник значительно превышает уровень зеркального отражения. Особенно заметен этот эффект при нормальном падении.
Заключение
В работе исследована эффективность метода связанных волн (RCWA) в расчетах отражения электромагнитных волн от двухпериодического радиопоглощающего материала, использующегося для покрытия стен в безэховых камерах, а также для дальнейшего использования при математическом моделировании компактных полигонов и их оптимизации. Характерными значениями таких радиопоглощающих материалов являются период порядка десяти длин волн и высота порядка тридцати длин волн.
Показано, что метод, вместе с некоторыми модификациями, позволяет решить задачу расчета отражательных характеристик радиопоглощающего материала. В качестве примера приведены результаты расчета коммерческого пирамидального материала. Рассмотрена сходимость алгоритма в зависимости от числа геометрических разбиений на слои и числа учтенных гармоник. Алгоритм верифицирован на аналогичной задаче путем сравнения результатов расчета с другими алгоритмами (методом моментов и методом конечных элементов). Сравнение эффективности этих подходов во многом показывает выигрыш метода связанных волн. Так же ясно, что метод даст большой выигрыш в скорости при расчете материалов с т.н. согласующими покрытиями. Кроме того, при некоторых углах падения алгоритм может быть усовершенствован и выполнять расчет еще быстрее [14, 15]. Также, важнейшим преимуществом алгоритма является то, что он позволяет получать поле каждой гармоники отдельно, а поскольку эти поля локализованы в разных областях пространства, можно рассматривать их при оптимизации также отдельно.
Литература
1. Балабуха Н.П., Зубов А.С., Солосин В.С. Компактные полигоны для измерения характеристик рассеяния. М.:Наука, 2007.
2. Никитенко А.В., Зубов А.С., Шапкина Н.Е. Оценка влияния отражения от поглощающего материала, размещенного вблизи облучателя коллиматора, на поле, измеряемое на апертуре коллиматора. Двенадцатая ежегодная научная конференция ИТПЭ РАН (Москва, 4-7 апреля 2011 г.): сб. тез. докл./ Рос. АН, Ин-т теоретич. и прикл. электродинамики, Научная конф. (12; 2011). - М.: ИТПЭ РАН, 2011.
3. Lifeng Li. Formulation and comparison of two recursive matrix algorithms for modeling layered diffraction gratings. // Opt. Soc. Am. A Vol. 13, No. 5/May 1996.
4. J.P. Hugonin, P.Lalanne, I. Delvillar, I.R. Matias. Fourier modal methods for modeling optical dielectric waveguides // Optical and Quantum Electronics (2005) 37:107–119.
5. E. Noponen, J. Turunen. Eigenmode method for electromagnetic synthesis of diffractive elements with three-dimensional profiles. // J. Opt. Soc. Am. A/Vol. 11, No. 9/September 1994.
6. D. Maystre. M. Neviere. Electromagnetic theory of crossed gratings // J. Optics (Paris), 1978, vol. 9, no 5, pp. 301-306.
7. Moraham M.G., Grann E.B., Pommet D.A., Gaylord T.K.. Formulation for stable and efficient implementation of the rigorous coupled-wave analysis of binary gratings. // J. Opt. Soc. Am. A 12, 1068-1076 (1995).
8. M. G. Moharam, T. K. Gaylord. Diffraction analysis of dielectric surface-relief gratings. // J. Opt. Soc. Am. 72 1385–1392 (1982).
9. А.В. Никитенко, А.С. Зубов, Н.Е. Шапкина. Моделирование электромагнитного рассеяния на радиопоглощающем материале методом связанных волн. //Математическое моделирование, 2014, том 26, номер 9, стр. 18-32.
10. Амитей Н., Галиндо В., Ву Ч. Теория и анализ фазированных антенных решеток. Издательство Мир, 1974.
11. Дж. А. Стреттон, Теория электромагнетизма. // ОГИЗ Москва, 1948.
12. P. Lalanne, G.M. Morris. Highly improved convergence of the coupled-wave method for TM polarization. // J. Opt. Soc. Am. A 13, 779-784 (1996).
13. Moraham M.G., Grann E.B., Pommet D.A., and Gaylord T.K.. Stable implementation of the rigorous coupled-wave analysis for surface-relief gratings: enhanced transmittance matrix approach. // J. Opt. Soc. Am. A 12, 1077-1086 (1995).
14. Benfeng Bai, Lifeng Li. Group-theoretic approach to enhancing the Fourier modal method for crossed gratings with C4 symmetry. // J. Opt. A: Pure Appl. Opt. 7 (2005) 783–789.
15. Benfeng Bai, Lifeng Li. Reduction of computation time for crossed-grating problems: a group-theoretic approach. // J. Opt. Soc. Am. A/Vol. 21, No. 10/October 2004.