УДК 621.396.49
ЭКСПЕРИМЕНТАЛЬНЫЙ АНАЛИЗ МЕТОДОВ ОПИСАНИЯ ДИНАМИКИ ДЛЯ МУЛЬТИМАРКОВО-ПОЛИГАУССОВЫХ ВЕРОЯТНОСТНЫХ МОДЕЛЕЙ
С. В. Козлов
Казанский национальный исследовательский технический университет им. А.Н. Туполева
Статья получена 9 декабря 2014 г.
Аннотация. В статье проводятся выбор и обоснование метода описания динамики для мультимарково-полигауссовой вероятностной модели на базе результатов экспериментального сравнительного анализа среднеквадратического отклонения предсказания квадратурных компонент сигналов системы CDMA One.
Ключевые слова: Марковские процессы, смеси, полигауссовы, CDMA, мультимарково-полигауссова модель, модель Джейкса, линейная нестационарная фильтрация, Калман.
Abstract: This article provides justification of the chosen method to describe the dynamics of Multi-Markov poly-Gaussian probabilistic model. This model is based on the experimental data of the comparative analysis for the standard deviation of the quadrature signal prediction of the CDMA One signal components.
Keywords: Markov processes, poly-Gaussian, CDMA, Multi-Markov poly-Gaussian model, Jakes model, linear non-stationary filtration, Kalman.
Введение
Основной особенностью подкласса мультимарково-полигауссовых моделей (ММ-ПГ) от других полигауссовых моделей [1], является использования в качестве элементарных компонент марковских последовательностей. Для повышения эффективности алгоритмов приёма, базирующихся на указанной модели, важным является возможность эффективного предсказания параметров компонент в условиях динамично меняющейся обстановки в мобильных сетях связи. В работе [1] для этих целей предлагается использовать фильтр Калмана, обеспечивающий линейное предсказание квадратурных компонент сигналов. В [2] обосновывается достаточность использования в технических задачах фильтра Калмана первого порядка для предсказания квадратурных компонент сигналов системы CDMA One.
Проведённый в [3] анализ применения фильтра Калмана для предсказания параметров канала, описанных полигармонической моделью Джейкса для узкополосного беспроводного канала движущегося объекта, показывает наличие существенной погрешности оценки, не убывающей в процессе работы алгоритма приёма.
На основании полученных результатов, авторами [3] предлагается новый алгоритм оценки комплексного множителя канала на основе модели Джейкса, параметры которой оцениваются с помощью фильтра Калмана.
Анализ применимости выводов, сделанных в [3] для предсказания квадратурных компонент ММ-ПГ модели применительно к CDMA системам, показывает, что полосы частот и интервалы предсказания сигналов, использованный при моделировании системы с моделью Джейкса не соответствуют аналогичным параметрам сигналов использованным в [2].
Таким образом, на основе имеющихся данных нельзя однозначно сделать вывод об эффективности предложенных решений для оценки квадратурных компонент сигналов и, следовательно, проведение исследований, дающих ответ на этот вопрос, является актуальным.
Постановка задачи
Целью работы является
проведение сравнительного анализа отклонений методов непосредственной оценки
квадратурных компонент и использования модели Джейкса для широкополосных
сигналов систем с кодовым разделением каналов на длительности кодового символа
для порядка моделей 
.
Условия моделирования
В качестве исходных данных рассматривались значения квадратурных компонент пилотного канала
,
полученные с помощью комплекса «CDMA Analyzer» на основе обработки сигналов сети CDMA One, записанных в различных точках города Казани. На основе каждой записи вычислялось около 350 000 значений квадратурных компонент. Для снижения влияния нескольких базовых станций при проведении исследования выбирались точки, где принимался сигнал только одной базовой станции.
Сравниваемые модели были записаны в следующем виде:
1. модель непосредственной оценки квадратурных компонент с использованием фильтра Калмана:
, (2)
где
-
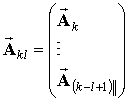вектор столбец 
последовательных
оценок квадратурных компонент пилотного канала до 
-го
кодового символа включительно,
-
матрица выделения
квадратурных компонент -го кодового символа из вектора 
,
-
вектор отсчётов шума измерения,
-
матрица предсказания,
- вектор отсчётов формирующего
шума;
2. модель оценки квадратурных компонент с использованием модели Джейкса:
, (3)
, (4)
где 
- -й
вектор столбец оценок квадратурных компонент квазигармонических составляющих
пилотного канала,
-
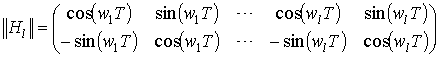матрица модуляции для частоты
квазигармонической составляющей 
и периода предсказания
, -
вектор отсчётов шума измерения,
- вектор отсчётов
формирующего шума.
Для проведения сравнения первоначально необходимо определить неизвестные параметры моделей.
Для первой модели к ним
следует отнести матрицу предсказания 
, которая была получена
на основе вычисленных коэффициентов авторегрессии [2]:
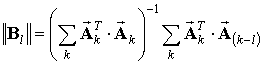. (5)
Для использования второй модели
необходимо знать значения частот квазигармонических составляющих , которые выбирались равномерно
распределёнными и вычислялись также на основе коэффициентов авторегрессии
первого порядка по формуле:
, 
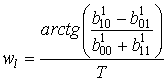. (6)
На основе полученных
параметров производилась фильтрация последовательности квадратурных компонент
пилотного канала с использованием обеих моделей и вычислялась относительная
погрешность оценивания 
:
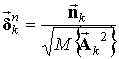, (7)
где 
-
обозначение математического ожидания.
Результаты моделирования
С помощью «CDMA Analyzer» были проведены операции, заданные
выражениями (1 - 7) для типичных записанных сигналов, снятых в различных точках
города Казани, и порядка модели 
.
Причем анализ 
осуществлялся независимо на
каждом участке стационарности каждого луча.
Графики зависимости СКО от порядка моделей для выбранных точек наблюдения, рассчитанные по обеим моделям по сравнению со значениями отклонений оценок авторегрессии из [2], приведёны на рисунках 1-4.
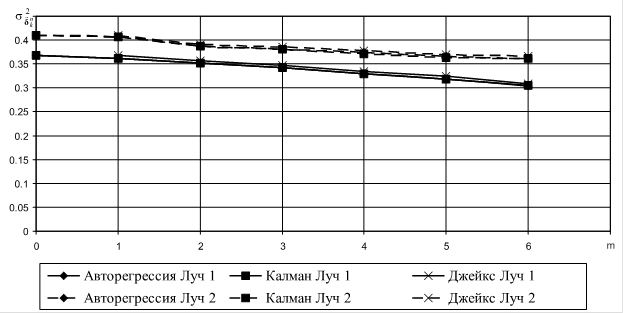
Рис. 1. Зависимость СКО относительной
погрешности оценки для точки 1.
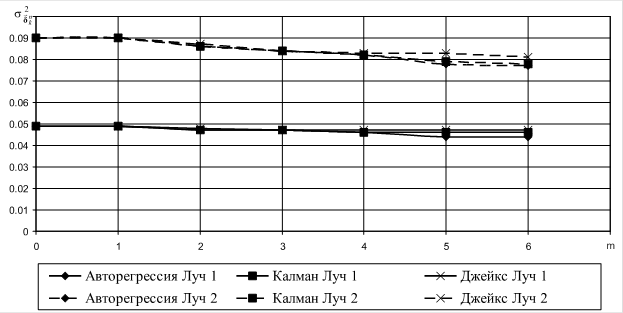
Рис. 2. Зависимость СКО относительной
погрешности оценки для точки 6.
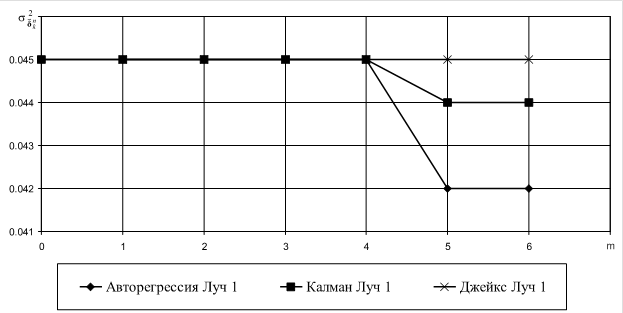
Рис. 3.
Зависимость СКО относительной погрешности оценки для точки
15.
В приведённых результатах отсутствует информация по второму лучу сигнала, снятого в точке 15, из-за малого объёма выборки (второй луч фиксируется редко и в течение короткого временного интервала, не позволяющего оценить для него коэффициенты авторегрессии).
Рис. 4.
Зависимость СКО относительной погрешности оценки для точки
43.
Заключение
Приведённые графики иллюстрируют, что для случая оценки параметров квадратурных компонент на длительности кодового символа все три варианта обеспечивают практически одинаковое СКО относительной погрешности оценки для всех исследованных точек наблюдения и порядков моделей. Кроме того, СКО оценок Калмана, использующего только значения текущих отсчётов, ни в одной из исследованных ситуаций не превышает СКО, предложенного в [3] алгоритма, использующего модель Джейкса.
Следовательно, с учётом приведённого в [2] анализа влияния порядка марковского процесса, в качестве основной модели описания динамики квадратурных компонент можно принять гауссово-марковскую последовательность первого порядка с линейным предсказанием.
Литература
1. Козлов С.В. Мультимарково-полигауссовские модели и алгоритмы в широкополосных системах // Нелинейный мир. -2011. - Том №9.- №11.С.716-726.
2. Козлов С.В. Новые смесевые подходы к проектированию радиоинтерфейса систем связи. – Казань: ООО «Новое знание», 2014. – 132с.
3. Кондрашова С.Ф., Крейнделина В.Б. Полигармоническая фильтрация комплексного множителя канала в системах подвижной радиосвязи // Электросвязь. 2007. №5, С. 49-51.