"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 12, 2014

оглавление

УДК 621.396.96

Пороговый способ измерения скорости протяженных объектов в зоне контроля радиотехнических устройств ближнего действия

 

В. М. Артюшенко 1, В. И. Воловач 2

1 ГБОУ ВПО МО «Финансово-технологическая академия», г. Королев

2 ФГБОУ ВПО «Поволжский государственный университет сервиса», г. Тольятти

 

Статья получена 16 декабря 2014 г.

 

Аннотация. Рассмотрен и проанализирован пороговый способ измерения скорости движение протяженного объекта в зоне контроля радиотехнического устройства обнаружения  ближнего действия. Показано, что применение в нем дополнительного канала измерения скорости позволяет не только обнаруживать протяженный объект, но и измерять параметры его движения. Показано, что применение в канале амплитудной селекции доплеровского сигнала позволяет значительно уменьшить фазовый шум, повышая тем самым точность измерения скорости протяженного объекта. Получена оценка потенциально достижимой точности измерения скорости движения объекта устройством обнаружения ближнего действия.

Ключевые слова: пороговый способ, протяженный объект, доплеровский сигнал, канал измерения скорости, радиотехническое устройство обнаружения, статистические характеристики мгновенной частоты, амплитудный порог.

Abstract. The threshold method for measuring of motion speed of the extended object within detection area of the short-range radio location device reviewed and analyzed. It is shown that the using additional speed measurement channel therein not only allows to detect the extended object, but also allows to measure it’s motion parameters. It is shown that applying of the Doppler signal in the amplitude selection channel can significantly reduce the phase noise, thereby increasing the accuracy of speed measuring of the extended object. An estimation of the potentially achievable object speed measurement accuracy of the short-range location devices is obtained.

Key words: threshold method, extended object, Doppler signal, speed measurement channel, radio location device, statistical characteristics of instantaneous frequency, amplitude threshold.

Введение

В [1] отмечалось, что радиотехнические устройства обнаружения (РУО) ближнего действия могут быть оптимизированы, прежде всего, путем их адаптации. Один из путей адаптации связан с возможностью измерения скорости обнаруженного объекта, если обнаружение осуществляется на основе обработки доплеровского сигнала. В результате, помимо задачи обнаружения РУО будет выполнять также функции измерителя скорости. Измерение скорости, а в более широком смысле параметров движения объекта (ускорения, геометрических размеров объекта, местоположения), позволяет не только более точно решать основную задачу обнаружения объекта РУО, поскольку, например, появляются дополнительные данные об объекте, включая спектр сигнала обнаружения [2-4], но и прогнозировать его поведение по отношению к рубежам зоны контроля. Во многих случаях измерение параметров движения объекта представляет собой самостоятельную задачу [5], [6].

Далее будут рассмотрены некоторые аспекты реализации канала измерения скорости, которым могут быть дополнены обычные РУО.

1. Постановка задачи исследования

Известно [7, 8], что наличие в измерительном объеме одновременно нескольких «блестящих» точек и их случайное положение приводит к существенным флюктуациям частоты доплеровского сигнала, являющейся мерой скорости. Эти флюктуации, называемые фазовым шумом [9], могут достигать значительных величин и существенно ограничивают точность оценки скорости.

Анализ мгновенной частоты доплеровского сигнала, полученной от двух «блестящих» точек, движущихся с одинаковой скоростью, показал, что ее максимальные выбросы соответствуют минимуму амплитуды и, наоборот, при больших значениях огибающей сигнала его частота практически не изменяется.

На основании этих результатов был предложен и реализован [10] пороговый способ обработки доплеровского сигнала, заключающийся в том, что демодуляции подвергается только та его часть, амплитуда которой лежит выше некоторого наперед заданного порога. Значения скорости и промежуточные моменты времени определяются путем интерполяции результатов демодуляции.

Наглядное представление о существе этого способа дает рис. 1, где a–d – участки полезного сигнала.

Рассмотрим основные статистические характеристики мгновенной частоты в зависимости от порога и оценку достигаемого при этом выигрыша в точности измерения.

Задача решается для доплеровского сигнала, моделью которого является узкополосный нормальный случайный процесс вида

,                                          (1)

где  – огибающая сигнала;  – частота несущей;  – функция, отражающая закон фазовой (частотной) модуляции.

 

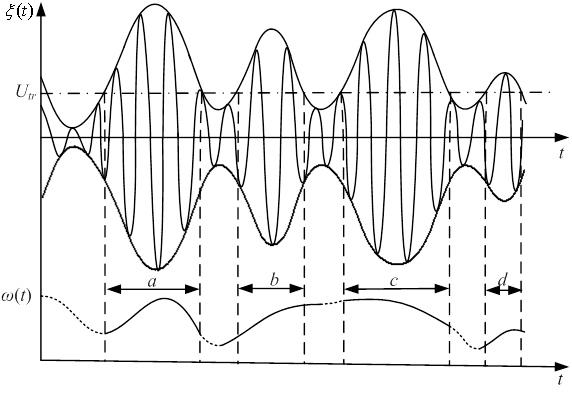
Рис. 1. Иллюстрация порогового способа обработки доплеровского сигнала

 

2. Статистические характеристики мгновенной частоты

Вначале найдем статистическую связь между случайными отклонениями частоты  и значениями огибающей . Двумерная плотность вероятности величин  и U может быть найдена на основании известного выражения [11] для четырехмерной плотности вероятности

,        (2)

где – дисперсия процесса (1),  – значение второй производной коэффициента корреляции в нуле.

Обычно считается, что , где  – полуширина спектра доплеровского сигнала на уровне  от его максимума. Интегрируя (2) по U и f в пределах ,  для U и – π, + π для  f, получим

.

Переходя к новой относительной переменной:

,

где  – средний квадрат огибающей, получим

.         (3)

На основании этого выражения найдем условную плотность вероятности частоты , когда значения огибающей сигнала превышают некоторый заданный порог (threshold (англ.) – «порог»). По определению [12] можно записать

.                                  (4)

Тогда

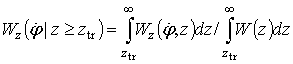,                           (5)

где  – одномерная плотность вероятности относительной огибающей.

В соответствии с [11]

.                                                      (6)

Подставляя (4) и (6) в (5) и вводя новую относительную переменную , представляющую собой флюктуацию мгновенной частоты [13], получим

.

Здесь ;– неполная гамма-функция.

Семейство плотностей вероятности флюктуации мгновенной частоты для различных уровней  приведено на рис. 2.

Из графиков видно, что с увеличением порогового уровня  резко уменьшается вероятность больших отклонений частоты и возрастает вероятность малых отклонений. Следовательно, величина среднеквадратичной ошибки с увеличением  должна снижаться.

 

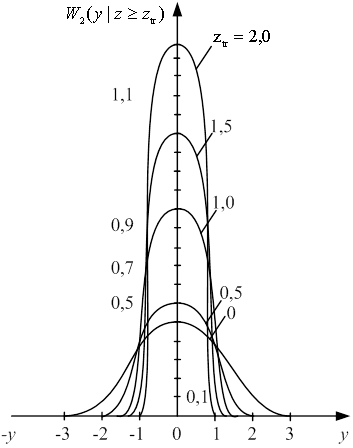
Рис. 2. Зависимости плотностей вероятности флюктуации мгновенной частоты от величины уровня заданного порога

 

Представляет интерес нахождение линии регрессии, устанавливающую зависимость математического ожидания модуля отклонений частоты от заданного значения огибающей.

По определению

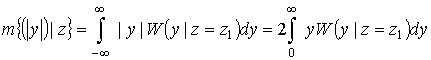,         (7)

где m – символ математического ожидания,  – плотность вероятности частоты при заданном значении . Подставляя в (7) значение , которое в соответствии с (4) равно

,

получим

.                                                   (8)

Как следует из (8), среднее значение модуля отклонений частоты  связано с относительным уровнем огибающей  обратно пропорциональной зависимостью.

Полученные результаты являются теоретическим обоснованием способа уменьшения фазового шума посредством амплитудной селекции доплеровского сигнала.

3. Оценка погрешности измерения частоты

Зависимость дисперсии отклонений частоты от порога может быть найдена из соотношения

,

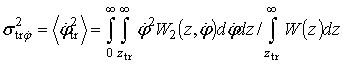где значения и определены выражениями (3) и (6).

С учетом последних можно записать

,                                   (9)

где  – интегральная показательная функция.

Относительное среднеквадратичное значение ошибки для мгновенной частоты как функции порога легко может быть найдено из (9):

.

Введя обозначение , получим:

,                         (10)

где М – любое целое положительное число.

Анализ зависимости (10) показывает, что среднеквадратичная ошибка  вначале быстро падает с увеличением порога, а затем ее крутизна уменьшается

На основании выражения (6) легко получить соотношение между длительностью  полезного сигнала и общей длительностью реализации :

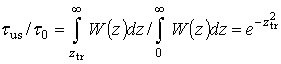,                                  (11)

где .

Из анализа зависимости (11) следует, что если при  длительность полезного сигнала составляет 0,37% от длительности реализации, то уже при  эта величина падает до 2%. Из изложенного можно сделать вывод о нецелесообразности установления , поскольку длительность полезного сигнала при этом будет составлять менее 10% от общей длительности реализации, а существенного снижения ошибки достигнуто не будет.

Погрешность измерения можно еще более снизить путем рациональной фильтрации сигнала на выходе частотного дискриминатора при условии, что известна корреляционная функция или спектральная плотность мгновенной частоты для заданного значения .

Спектральная плотность мгновенной частоты многочастотного доплеровского сигнала при беспороговом детектировании, как известно [9], эквивалентна спектральной плотности нормального узкополосного процесса. Ее значения в нуле S(0) максимальны и равны 4,66Δw [11].

Для беспорогового детектирования среднеквадратичная относительная ошибка определения мгновенной скорости v будет равна

,

где – среднеквадратическое отклонение частоты доплеровского сигнала;  – среднеквадратическое отклонение скорости объекта;  – частота доплеровского сигнала;  – диапазон изменения частоты доплеровского сигнала.

Для реальных значений и получим .

4. Анализ спектральной плотности частоты

Далее перейдем к анализу спектральной плотности частоты в пороговом режиме демодуляции. Вначале сделаем несколько предварительных замечаний. Как было показано, дисперсия частоты доплеровского сигнала в этом режиме конечна и падает с ростом порога. Следовательно, значения ее корреляционной функции в нуле, в отличие от беспороговой демодуляции, также конечны и будут падать с ростом порога. Конечность дисперсии предполагает, что интеграл от спектральной плотности фазового шума тоже конечен, а сама спектральная плотность падает быстрее, чем .

Поскольку корреляционная функция мгновенной частоты при нулевом пороге является монотонной и убывающей, можно полагать, что с ростом порога ее значения не только в нуле, но и во всех других точках начнут снижаться. Если это так, то спектральная плотность флюктуаций мгновенной частоты в нуле, представляющая собой интеграл от корреляционной функции будет падать в функции порога.

Учитывая, что полученное аналитическое выражение для корреляционной функции мгновенной частоты оказалось настолько сложным, что его анализ, даже с применением современных ПК, слишком дорог, для подтверждения полученных выводов количественными оценками был использован метод машинного моделирования. С его помощью было осуществлено моделирование доплеровского сигнала с определением текущих значений огибающей и мгновенной частоты на каждом временном шаге, с выделением участков сигнала с надпороговыми значениями огибающей и численными оценками корреляционной функции и спектральной плотности мгновенной частоты для рассматриваемых участков.

Расчет искомых значений случайной частоты осуществлялся в соответствии с известным [11] выражением

,

где  – соответственно синусная и косинусная компоненты и их производные по времени комплексной амплитуды  сигнала.

Вычисление каждой составляющей осуществлялось по следующим формулам:

;

;

;

.

В приведенных выражениях t – текущее время, дискретные значения которого на каждом временном шаге определяются как qh, h – интервал дискретности,  – огибающая сигнала одиночной блестящей точки,  – случайный момент прихода i-ой «блестящей» точки в центр измерительного объема, a – параметр, определяемый поперечным размером измеряемого объекта.

При известной длительности одночастотного сигнала, выраженной в доплеровских периодах , и заданном среднем числе частиц n, одновременно присутствующих в измерительном объеме, величина l находится как . Последовательные значения интервалов  и моментов прихода частиц  получались с помощью датчика случайных чисел в соответствии с выражениями

,

,

где  – случайное число, равновероятно распределенное в пределах [0,1], генерируемое датчиком случайных чисел. Оценка автокорреляционной функции частоты  при сдвиге qh (q – число шагов, h – интервал дискретности при отсутствии порогового ограничения огибающей) находилась как [14]

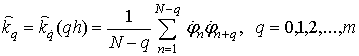.                                   (12)

Здесь N – число отсчетов реализации, m – максимальное число рассчитываемых точек корреляционной функции.

При введении порогового ограничения снизу по огибающей, часть сигнала с малыми амплитудами из рассмотрения исключалась, а значения случайной частоты на этих участках полагались равными нулю. Поэтому в выражение (12) для корреляционной функции частоты при введении порога должна быть внесена поправка, исключающая из общего числа слагаемых члены с нулевыми значениями произведений . Тогда

,

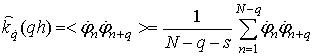где s – число нулевых произведений  (когда  либо  либо и то и другое значения  равны нулю).

Оценка спектральной плотности случайной компоненты мгновенной частоты сигнала в соответствии с [15] может быть найдена двумя способами:

1) стандартный способ, то есть, через Фурье-преобразование корреляционной функции;

2) способ прямого преобразования Фурье исходной реализации мгновенной частоты с использованием алгоритма быстрого преобразования Фурье (БПФ) (так называемый метод Кули и Тьюки), который является более эффективным с точки зрения быстродействия.

Исходя из требований обеспечения точности не менее 5% при оценках спектров и корреляционных функций и разрешения по частоте в спектральной области , были выбраны следующие значения параметров модели: число реализаций , длина реализации  точек, шаг дискретности .

Результаты проведенного численного анализа представлены на рис. 3 и 4.

 

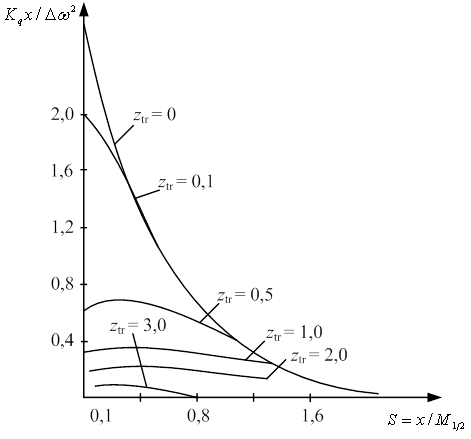
Рис. 3. Семейство корреляционных функций случайной частоты в зависимости от  относительного параметра S.

 

На рис. 3 показано семейство корреляционных функций случайной частоты, построенных в зависимости от относительного параметра , где , , при различных уровнях порогового ограничения огибающей. Показательно, что значения корреляционных функций для  в точности совпадают с теоретически рассчитанными значениями дисперсии частоты при соответствующих уровнях порога , а ход кривых при других значениях относительного сдвига S – с вышеприведенными предположениями.

На рис. 4 приведены графики спектральной плотности частоты  при различных величинах порога (буквы Т и М означают теоретические и моделированный результаты).

 

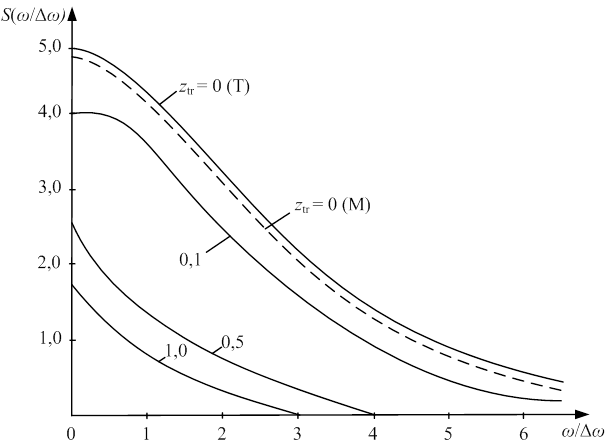
Рис. 4. Графики спектральной плотности частоты  при различных величинах порога

 

Видно, что с увеличением порога происходит как сужение спектра, так и уменьшение всех его абсолютных значений на соответствующих частотах. Изменение спектральной плотности в нуле  от порога аппроксимируется как

.

Следовательно, для  значение  будет уменьшено в 4,5 раза по сравнению со случаем . Это означает, что при исследовании турбулентных пульсаций скорости величина среднеквадратичной ошибки измерения скорости, определяемой в основном величиной , при введении порога будет снижена в  раза по сравнению со случаем, когда порог отсутствует, а полоса частот та же самая.

5. Выводы

Таким образом, проведенный теоретический и численный анализ позволяет дать оценки потенциально достижимой точности измерения, в общем случае параметров движения протяженных объектов, доплеровских устройств обнаружения ближнего радиуса действия в пороговом режиме демодуляции. Введение амплитудного порога в отличие от беспороговой демодуляции доплеровского сигнала позволяет получить конечные значения дисперсии оценок скорости движения протяженного объекта, в зоне действия устройства обнаружения, в широкой полосе частот и уменьшает все спектральные компоненты фазового шума.

 

Литература
 

1.     Воловач В.И. Характеристики обнаружения радиотехнических устройств охраны и повышение эффективности их работы посредством адаптации к изменяющейся помеховой обстановке // Электротехнические и информационные комплексы и системы. 2011, т. 7, № 3. С. 25-30.

2.     Артюшенко В.М., Воловач В.И. Анализ параметров спектра сигнала, отраженного от протяженного объекта // Известия вузов. Приборостроение. 2012, т. 55, № 9. С. 62-67.

3.     Артюшенко В.М., Воловач В.И., Иванов В.В. Статистические характеристики сигналов и помех в радиотехнических устройствах ближнего действия // Известия вузов. Приборостроение. 2014, т. 57, № 7. С. 46-50.

4.     Артюшенко В.М., Воловач В.И. Экспериментальное исследование параметров спектра доплеровского сигнала, отраженного от протяженного объекта // Прикаспийский журнал: управление и высокие технологии. 2012, № 3(19). С. 17-24.

5.     Артюшенко В.М., Воловач В.И. Анализ условий работы системы контроля заполнения путей и ее информационного обеспечения // Научно-технический вестник Поволжья. 2012, № 6. С. 115-119.

6.     Артюшенко В.М., Воловач В.И. Динамические модели параметров движения протяженных объектов // Электротехнические и информационные комплексы и системы. 2014, т. 10, № 2. С. 84-90.

7.     Островитянов Р.В., Басалов Ф.А. Статистическая теория радиолокации протяженных целей. М.: Радио и связь, 1982. 232 с.

8.     Фельдман Ю.И., Мандуровский И.А. Теория флюктуаций локационных сигналов, отраженных распределенными целями. М.: Радио и связь, 1988. 272 с.

9.     Соболев В.С. О спектре фазового шума на выходе лазерного доплеровского измерителя скорости // Автометрия. 1974, № 6. С. 23-28.

10.  Лазерные доплеровские измерители скорости. Новосибирск: Наука, 1975. 128 с.

11.  Тихонов В.И. Статистическая радиотехника. М.: Радио и связь, 1982. 624 с.

12.  Вентцель Е.С. Теория вероятностей. М.: Наука, 1964. 814 с.

13. Воловач В.И. Плотность распределения мгновенной частоты глубоко федингующего сигнала // Сборник научных трудов ГАСБУ "Проблемы повышения качества в сфере сервиса". М.: ГАСБУ, 1997. С. 48-52.

14.  Бендат Дж., Пирсол А. Измерение и анализ случайных процессов. М.: Мир, 1974. 326 с.

15. Артюшенко В.М. Исследование и разработка радиолокационного измерителя параметров движения протяженных объектов. М.: ГБОУ ВПО ФТА, 2013.214 с.