ЧИСЛЕННЫЙ АНАЛИЗ ОТРАЖЕНИЙ ПЛОСКОЙ ПОЛЯРИЗОВАННОЙ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ ОТ НЕОДНОРОДНОГО СЛОЯ МАГНИТОДИЭЛЕКТРИКА
Государственное образовательное учреждение высшего профессионального образования
"Поволжская государственная академия телекоммуникаций и информатики"
Кафедра Теоретических основ радиотехники и связи
Получена 31 января 2007 г.
Предложена методика численного моделирования взаимодействия электромагнитного излучения с неоднородным слоем магнитодиэлектрика. Получено дифференциальное уравнение для коэффициента отражения волны от усеченного слоя.
Введение
В области практических приложений теории электромагнитных волн наиболее характерны задачи об их взаимодействии с неоднородными и нелинейными средами [1]. В последнее время наиболее актуальным является вопрос о создании малоотражающих покрытий, применяемых в качестве экранирования большинства приборов и устройств техники СВЧ от воздействия электромагнитного излучения [2]. Так, например, в работе [3] предложено использование экспоненциально неоднородного слоя магнитодиэлектрика, нанесенного на металл, для создания практически не отражающего радиоволны покрытия. В настоящей работе проведен численный анализ отражений от такого слоя, но при произвольном угле падения электромагнитной волны с Е и H-поляризацией, причем величину волнового сопротивления среды, на которую нанесен магнитодиэлектрик, мы можем варьировать.
Наклонное падение электромагнитной волны с Н–поляризацией на слой неоднородного магнитодиэлектрика
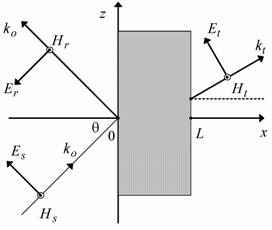
Рассмотрим электродинамическую систему, представляющую собой слой магнитодиэлектрика, расположенный в координатных плоскостях декартовой системы координат (рис.1).
Рис. 1. Наклонное падение электромагнитной волны Н-поляризации на слой неоднородного магнитодиэлектрика
Левая граница слоя находится в плоскости
, а правая –
. В дальнейшем пространство
, будем обозначать как область 1, а пространство
, как область 2. В области 1 на границу слоя под углом
падает плоская волна с Н-поляризацией, с напряженностью электрического
и магнитного
полей, описываемыми выражениями:
,
,
,
где
– волновое сопротивление области 1,
– волновое число в вакууме.
Кроме падающей волны в области 1 в общем случае существует также отраженная волна, имеющая y-компоненту магнитного поля и x-компоненту, z-компоненту напряженности электрического поля.
,
,
,
где
– коэффициент отражения в случае Н-поляризации.
В области 2 существует только одна бегущая волна:
,
,
,
где
– коэффициент прохождения в случае Н-поляризации,
– волновое число в области 2,
– волновое сопротивление области 2.
В неоднородном слое магнитодиэлектрика пространственные зависимости y-составляющей напряженности магнитного поля и z-составляющей напряженности электрического поля описываются первыми двумя уравнениями Максвелла, которые для гармонических полей имеют вид:
Для удобства дальнейших расчетов проведем нормировку этой системы.
– нормированная координата,
– нормированное волновое число,
– нормированная напряженность электрического поля,
– нормированная напряженность магнитного поля.
Уравнения Максвелла можно записать следующим образом:
Представим уравнения Максвелла в компактном виде:
Для уравнений (1), исходя из условий непрерывности тангенциальных составляющих напряженностей полей, записываются следующие граничные условия:
Наклонное падение электромагнитной волны с Е–поляризацией на слой неоднородного магнитодиэлектрика
Падающая на слой под углом
к его нормали электромагнитная волна Е-поляризации имеет только одну составляющую вектора напряженности электрического поля
и две составляющих вектора напряженности магнитного поля
. Лежащие в плоскости слоя проекции векторов описываются выражениями:
,
,
.
Соответствующие проекции в отраженной волне записываются в виде:
,
,
,
где
– коэффициент отражения в случае Е-поляризации.
А для прошедшей слой волны имеем:
,
,
,
где
– коэффициент прохождения в случае Е-поляризации,
– волновое число в области 2,
– волновое сопротивление области 2.
В неоднородном слое магнитодиэлектрика пространственные зависимости y-составляющей напряженности электрического поля и z-составляющей напряженности магнитного поля описываются первыми двумя уравнениями Максвелла, которые для гармонических полей имеют вид:
Для удобства дальнейших расчетов проведем нормировку этой системы.
– нормированная напряженность электрического поля,
– нормированная напряженность магнитного поля.
Уравнения Максвелла можно записать следующим образом:
Представим уравнения Максвелла в компактном виде:
Для уравнений (3), исходя из условий непрерывности тангенциальных составляющих напряженностей полей, записываются следующие граничные условия:
Дифференциальное уравнение для коэффициента отражения
Системы уравнений (1) и (3) вместе с условиями (2) и (4) составляют граничные задачи, решение которых позволяет определять волновые поля в слое магнитодиэлектрика. При изменении волнового числа
можно рассчитать частотные зависимости коэффициентов отражения
и
слоя. Однако (1) и (3) являются уравнениями с переменными коэффициентами, и их аналитическое решение возможно только для небольшого числа модельных зависимостей
и
. Численное решение задачи целесообразно проводить, перейдя от уравнений (1), (3) к дифференциальным уравнениям [4] для коэффициентов отражения от усеченного слоя, расположенного между текущей плоскостью
и задней границе слоя
. Для уравнений (3) переход к уравнению для обобщенного коэффициента отражения выглядит следующим образом.
Предположим, что решения связаны следующей зависимостью:
.
Тогда из граничных условий (4) следует, что
.
Распространим последнюю связь на произвольное сечение
:
.
В предположении, что слева от рассматриваемой плоскости магнитодиэлектрик отсутствует,
представляет собой коэффициент отражения от усеченного слоя. На основе системы (3) нетрудно записать уравнение для
.
Аналогичным образом получаем уравнение для коэффициента отражения волны Н-поляризации:
Нелинейные уравнения (5), (6) численно интегрируются до
с начальными условиями вида:
Значения
дают истинные величины коэффициентов отражения. Таким образом, граничная задача для волновых полей сведена к задаче Коши для обобщенного коэффициента отражения. Отметим, что в условиях (7) мы можем варьировать значение волнового сопротивления области 2. Например, можно смоделировать область 2 как металл, т.е.
При этом условия (7) могут быть записаны в виде:
Полученные уравнения (5), (6) представляют собой комплексное уравнение Риккати, и при его интегрировании можно использовать одно из численных частных решений [5].
Результаты расчетов и выводы
В качестве примера применения предложенного метода приведем результаты расчетов для экспоненциального слоя магнитодиэлектрика, задаваемого следующим образом:
,
,
где
– начальные значения проницаемостей на поверхности слоя,
.
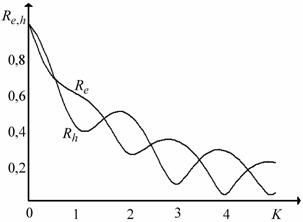
На рис. 2 приведены графики частотных зависимостей модулей коэффициентов отражения
,
для значений параметров слоя
,
и угле падения
, причем
. Данные частотной зависимости могут служить в экспериментах по электромагнитной диагностике слоя магнитодиэлектрика, располагающегося на поверхности металла.
Рис. 2. Частотные зависимости модулей коэффициентов отражения волны Е и Н-поляризации
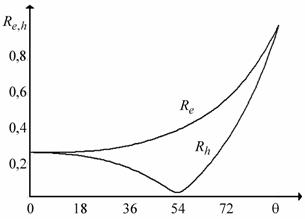
На рис. 3 приведены графики угловых зависимостей модулей коэффициентов отражения
,
для тех же значений параметров слоя и нормированной частоте
.
Рис. 3. Угловые зависимости модулей коэффициентов отражения волны Е и Н-поляризации
Литература
1. Вильхельмссон Х. Когерентное нелинейное взаимодействие волн в плазме. – М.: Энергоиздат, 1981. – 229 с.
2. Пирумов В.С., Алексеев А.Г., Айзикович Б.В. – Новые радиопоглощающие материалы и покрытия. / Зарубежная радиоэлектроника № 6, 1994. – С. 2-8.
3. Лаговский Б.А., Мировицкий Д.И. – Малоотражающий экспоненциальный слой магнитодиэлектрика. / Радиотехника и электроника Т.43., №1, 1998. – С. 609-612.
4. Зайцев В.В., Панин Д.Н., Яровой Г.П. Поляризационные эффекты при отражении электромагнитной волны от неоднородного плазменного слоя. / Электродинамика и техника СВЧ и КВЧ. Вып. 2 (23). – 1999. – С. 72-73
5. Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление. – М.: Наука, 1969. – 320 с.
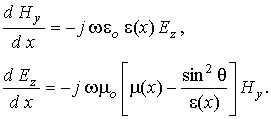
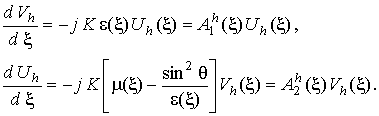
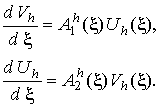 (1)
(1)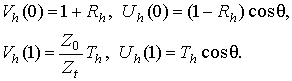 (2)
(2)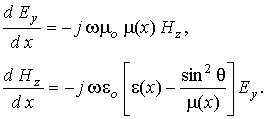
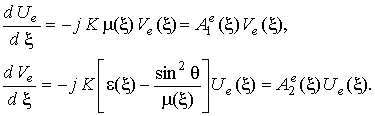
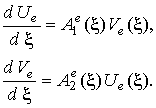 (3)
(3)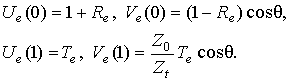 (4)
(4)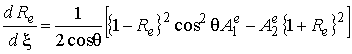 (5)
(5)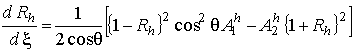 (6)
(6)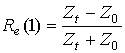 ,
,
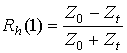 . (7)
. (7)