ЭЛЕКТРОМАГНИТНЫЕ ПОВЕРХНОСТНЫЕ ВОЛНЫ НА ГРАНИЦАХ РЕЛЯТИВИСТСКИ ДВИЖУЩЕГОСЯ СЛОЯ ПЛАЗМЫ
С. Н. Марышев1, Н. С. Шевяхов2
1Московский физико-технический институт, 2Ульяновский филиал Института радиотехники и электроники им. В.А.Котельникова РАН
Получена 4 февраля 2010 г.
Аннотация. Обсуждаются релятивистские эффекты распространения поверхностной электромагнитной ТМ-волны вдоль слоя изотропной бесстолкновительной плазмы, поперечно движущегося в вакууме. Показано, что в лабораторной системе отсчета поверхностная волна вместе с доплеровским повышением частоты претерпевает поворот волновой нормали в сторону движения слоя. Установлено, что в результате линейных релятивистских вкладов электрического и магнитного полей в поляризуемость плазмы вдоль слоя в спектре мод лабораторной системы отсчета к частотной отсечке добавляется снизу отсечка спектра по волновому числу, интерпретируемые вместе как проявление релятивисткой неразрывности пространственно-временного континуума.
Ключевые слова: электромагнитная поверхностная волна, движущаяся плазма, релятивистские эффекты, дисперсия.
Введение
Интерес к электромагнитным волнам в нестационарной плазме ограничивается обычно потоковыми эффектами, когда течение плазмы вдоль границ происходит без изменения их геометрии и местоположения [1]. В работах [2-4] на примере бегущих фронтов фотоионизации разреженной среды рассматривался обратный случай поперечного перемещения границ электронной плазмы, сохраняющей состояние покоя. Из-за кинетических эффектов в плазме структура границ в этих условиях существенно зависит от скорости движения. Именно, при около световых скоростях фронты фотоионизации сильно "размазываются" в силу сравнительно большого времени жизни фотоэлектронов в разреженной среде. Рассмотрение релятивистских эффектов теряло, поэтому, смысл.
Возможность
релятивистского подхода к изучению влияния поперечного движения плазмы на
распространение поверхностных волн предоставляет, однако, перемещение плазмы
как целого. Для полубесконечной плазмы соответствующая релятивистская задача
рассматривалась недавно в [5]. На практике приходится иметь дело с плазменными
сгустками конечной толщины. Лабораторный способ получения релятивистских
сгустков с хорошо выраженными границами испарением металлических пленок под
воздействием мощного лазерного излучения известен давно [6]. В настоящей статье
результаты работы [5] обобщаются на случай плазменного сгустка конечной
толщины, движущегося с релятивистской скоростью V![]() c, c
– скорость света. Другая причина, побуждающая вернуться к проблеме, затронутой
в [5], состоит в недостаточной ясности отдельных ее аспектов по причине
ограниченности цитируемой работы рамками краткого сообщения.
c, c
– скорость света. Другая причина, побуждающая вернуться к проблеме, затронутой
в [5], состоит в недостаточной ясности отдельных ее аспектов по причине
ограниченности цитируемой работы рамками краткого сообщения.
Формулировка задачи и исходные уравнения
В волновых задачах с
движущимися границами [7] почти всегда процессы и состояние сред приходится
описывать в двух системах отсчета: лабораторной системе x0yz с фиксированным положением регистрирующего прибора, и
попутной ![]() – с
фиксированным положением границ. Поперечное движение плазмы как целого отличается
от рассмотренного в задачах [2-4] тем, что позволяет выделить в качестве
системы покоя, общей для плазмы и ее границ, попутную систему отсчета.
Очевидно, что с позиции наблюдателя в этой системе отсчета мы имеем дело с
граничной задачей для неподвижного слоя плазмы, решение которой для
поверхностных ТМ-волн хорошо известно [8]. Предпринятое исследование состоит,
фактически, в пересчете волновых полей указанного решения в лабораторную
систему отсчета.
– с
фиксированным положением границ. Поперечное движение плазмы как целого отличается
от рассмотренного в задачах [2-4] тем, что позволяет выделить в качестве
системы покоя, общей для плазмы и ее границ, попутную систему отсчета.
Очевидно, что с позиции наблюдателя в этой системе отсчета мы имеем дело с
граничной задачей для неподвижного слоя плазмы, решение которой для
поверхностных ТМ-волн хорошо известно [8]. Предпринятое исследование состоит,
фактически, в пересчете волновых полей указанного решения в лабораторную
систему отсчета.
В попутной системе отсчета полевые и, где это необходимо, – параметры плазмы, условимся помечать тильдой сверху. Соответственно, имеем в качестве исходных систему уравнений Максвелла для электромагнитного поля плазмы [7-9]
В гидродинамическом бесстолкновительном приближении к ней добавим линеаризованные уравнение движения плазмы [8]
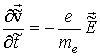 (2)
(2)
и уравнение неразрывности
![]() . (3)
. (3)
В уравнениях
(1)-(3) ![]() и
и![]() – напряженности
электрического и магнитного полей,
– напряженности
электрического и магнитного полей, ![]() – скорость смещения электронов плазмы, n – малое (n
– скорость смещения электронов плазмы, n – малое (n![]() n0) отклонение концентрации электронов от равновесного значения
n0, me – масса, а e
– элементарный заряд. Дополнительно учтем выражение для плотности тока
n0) отклонение концентрации электронов от равновесного значения
n0, me – масса, а e
– элементарный заряд. Дополнительно учтем выражение для плотности тока
![]() . (4)
. (4)
Уравнения (2)-(4) соответствуют элементарной модели, в которой плазма рассматривается как идеальная и изотропная электронная жидкость. Грубость избранного подхода, оправданного для слабых возмущений при низких температурах и отсутствии внешних магнитных полей, искупается простотой модели. Вместе с тем, как будет показано ниже, она вынуждает особенно тщательно отнестись к релятивистским преобразованиям величин при переходе из попутной в лабораторную систему отсчета.
Плазма занимает область ![]() (рис.1, d – толщина слоя) и за ее пределами уравнения (1)-(4)
заменим уравнениями для электромагнитного поля в вакууме. Они аналогичны
уравнениям (1), где
(рис.1, d – толщина слоя) и за ее пределами уравнения (1)-(4)
заменим уравнениями для электромагнитного поля в вакууме. Они аналогичны
уравнениям (1), где ![]() ,
а полевые характеристики снабжены, для отличия, нижним индексом 0. Граничные условия
выразим стандартным требованием непрерывности тангенциальных составляющих напряженностей
полей [8,9]. Для волн ТМ-поляризации это x-составляющая напряженности электрического и z-составляющая напряженности магнитного
полей. Удобнее использовать импедансную форму граничных условий, основываясь на
определения импеданса Z
плазмы и Z0 вакуума равенствами
,
а полевые характеристики снабжены, для отличия, нижним индексом 0. Граничные условия
выразим стандартным требованием непрерывности тангенциальных составляющих напряженностей
полей [8,9]. Для волн ТМ-поляризации это x-составляющая напряженности электрического и z-составляющая напряженности магнитного
полей. Удобнее использовать импедансную форму граничных условий, основываясь на
определения импеданса Z
плазмы и Z0 вакуума равенствами
В таком случае граничные условия задачи примут вид
Оговоримся, что
при использовании равенств (5), (6) подразумевается представление гармонических
колебаний экспонентой ![]() ,
где w – частота, а
,
где w – частота, а ![]() – время, отсчитываемое наблюдателем в
попутной системе отсчета.
– время, отсчитываемое наблюдателем в
попутной системе отсчета.
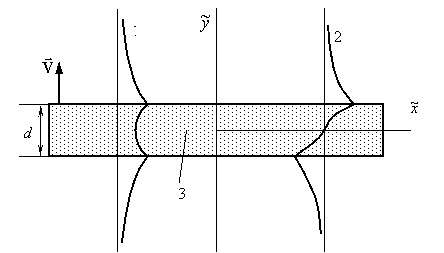
Рис. 1. Геометрия задачи и распределение продольной компоненты
электрического поля поперек слоя плазмы 3 в поверхностной ТМ-волне:
1 – симметричная мода, 2 – антисимметричная мода.
Определение импедансов по формулам (5) требует знания связей z- и x-компонент
соответственно магнитного и электрического полей. С этой целью обратимся к
уравнениям Максвелла (1), из которых в результате исключения ![]() и
и ![]() имеем соотношение
для плотности тока
имеем соотношение
для плотности тока
где We – плазменная частота. Благодаря (7)
при определении полей в плазме можно ограничиться двумя первыми уравнениями
(1). Замечая, что ![]() ,
, ![]() , напишем в составляющих
, напишем в составляющих
Аналогичные уравнения для полей в вакууме формально соответствуют равенствам (8), где компоненты напряженностей снабдим дополнительно нижним индексом 0, а также примем g=0. Уравнения (8) потребуются в дальнейшем для установления полей поверхностной ТМ-волны и определения импедансов по формулам (5).
Поверхностная ТМ-волна в попутной системе отсчета
Единственность компонент полей ![]() и
и ![]() делает предпочтительным их использование
для представления решения. Для поля в плазме, как следует из уравнений (1), (7),
имеем
делает предпочтительным их использование
для представления решения. Для поля в плазме, как следует из уравнений (1), (7),
имеем
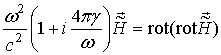 ,
,
или учитывая
равенство ![]() , получим
, получим
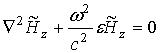 . (9)
. (9)
Здесь величина
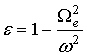 (10)
(10)
представляет собой диэлектрическую проницаемость плазмы. Уравнение (9) является исходным для определения поля в слое плазмы. В вакууме – среде с единичной проницаемостью, в (9) следует принять e=1 и к индексу z добавить 0.
Принимая, что ![]() ~
~![]() ,
,![]() , из требования ограниченности полей в областях определения
получим на основании (9)
, из требования ограниченности полей в областях определения
получим на основании (9)
Волновое
число k и коэффициенты локализации полей s и ![]() поверхностной ТМ-волны при спадании полей
от границ слоя в плазму и вакуум соответственно связаны при этом равенствами
поверхностной ТМ-волны при спадании полей
от границ слоя в плазму и вакуум соответственно связаны при этом равенствами
Согласно (5) и вытекающим с учетом (11), (12) из (8) связям компонент электрических и магнитных полей напишем
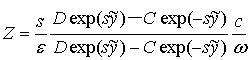 , (14)
, (14)
![]() . (15)
. (15)
В выражении
(15) для верхней границы ![]() выбирается верхний знак и,
соответственно, – нижний знак, если
выбирается верхний знак и,
соответственно, – нижний знак, если ![]() . Подстановка (14), (15) в граничные условия (6) дает систему
алгебраических уравнений, из которых исключением отношения амплитудных
коэффициентов D/C приходим к равенству
. Подстановка (14), (15) в граничные условия (6) дает систему
алгебраических уравнений, из которых исключением отношения амплитудных
коэффициентов D/C приходим к равенству
Оно представляет искомое дисперсионное соотношение для поверхностной ТМ-волны слоя плазмы в попутной системе отсчета, где x=sd/2 .
Ввиду (13) e=(k2-s2)/(k2-s02) и замечая, что ![]() ,
,
уравнению (16) можно придать вид
Выражение
(17) показывает, что существует два типа (моды) поверхностных электромагнитных
волн, удерживаемых слоем. При знаке "плюс" поверхностная волна
характеризуется симметричным распределением продольной компоненты
электрического поля ![]() поперек слоя [12] (профиль 1 на рис.
1), – симметричная мода. При знаке "минус" имеет место антисимметричное
распределение поля
поперек слоя [12] (профиль 1 на рис.
1), – симметричная мода. При знаке "минус" имеет место антисимметричное
распределение поля ![]() с профилем 2 и мода называется
антисимметричной.
с профилем 2 и мода называется
антисимметричной.
Спектр мод по формулам (17) можно рассчитать численно. Достаточно
выразить s через s0, используя равенство ![]() , которое вытекает из соотношений (13).
Тогда равенства (17) принимают форму трансцендентных уравнений, корни которых
по заданному k позволяют
найти соответствующее значение s0.
Дальнейшее очевидно: по формуле, связывающей s и s0 , пересчитывается величина s, а затем согласно любому из соотношений
(13) рассчитывается частота, определяя, таким образом, дисперсионный спектр w=w(k) мод поверхностной электромагнитной волны.
Вместе с представлением полей выражениями (11), (12) и связями компонент (8)
определение дисперсионного спектра мод исчерпывает описание поверхностной
ТМ-волны в попутной системе отсчета.
, которое вытекает из соотношений (13).
Тогда равенства (17) принимают форму трансцендентных уравнений, корни которых
по заданному k позволяют
найти соответствующее значение s0.
Дальнейшее очевидно: по формуле, связывающей s и s0 , пересчитывается величина s, а затем согласно любому из соотношений
(13) рассчитывается частота, определяя, таким образом, дисперсионный спектр w=w(k) мод поверхностной электромагнитной волны.
Вместе с представлением полей выражениями (11), (12) и связями компонент (8)
определение дисперсионного спектра мод исчерпывает описание поверхностной
ТМ-волны в попутной системе отсчета.
Поверхностная ТМ-волна в лабораторной системе отсчета
Лабораторную систему отсчета x0yz, в которой координаты, время и компоненты полей условимся писать без тильды сверху, свяжем с приемной антенной. Рассмотрение в ней полей и спектра мод поверхностной волны – необходимый элемент исследования, так как именно этой форме представления волны соответствуют характеристики, определяемые в эксперименте.
Учитывая, что движение плазмы происходит вдоль оси y, для перехода в лабораторную систему отсчета воспользуемся преобразованиями Лоренца [9,10]
Согласно (18)
несложно установить вид фазы колебаний компонент полей волны в лабораторной
системе отсчета. Однако с подстановкой величин ![]() и
и ![]() из (18) в выражения (11), (12) мы еще
имеем дело с амплитудами полей попутной системы отсчета. Таким образом, в
формулах (11), (12) и им соответствующим компонентам электрических полей нужно
предварительно перейти к значениям
из (18) в выражения (11), (12) мы еще
имеем дело с амплитудами полей попутной системы отсчета. Таким образом, в
формулах (11), (12) и им соответствующим компонентам электрических полей нужно
предварительно перейти к значениям ![]() и
и ![]() ,
записанным в лабораторной системе отсчета.
,
записанным в лабораторной системе отсчета.
Обратимся с этой целью к формулам релятивистского преобразования полей [9,10]:
Индексы || и ![]() в них означают соответственно
параллельность и перпендикулярность компонент движению плазмы. В случае вакуума
компоненты полей в формулах (19), (20) нужно, конечно, снабдить индексом 0
снизу.
в них означают соответственно
параллельность и перпендикулярность компонент движению плазмы. В случае вакуума
компоненты полей в формулах (19), (20) нужно, конечно, снабдить индексом 0
снизу.
Для поверхностной ТМ-волны в попутной системе отсчета имеет место
ортогональность электрического и магнитного полей. Комбинация величин ![]() (
(![]() в попутной системе
отсчета) образуют релятивистский инвариант. Поэтому данное качество волны сохранится
и в лабораторной системе отсчета. С учетом того, что индукции полей в попутной
системе отсчета равны
в попутной системе
отсчета) образуют релятивистский инвариант. Поэтому данное качество волны сохранится
и в лабораторной системе отсчета. С учетом того, что индукции полей в попутной
системе отсчета равны ![]() ,
,![]() ,
,![]() ,
, ![]() на основании (19) заключаем:
на основании (19) заключаем:
тогда как y-составляющие магнитных полей
отсутствуют. Из условия ![]() (
(![]() ) также следует
) также следует
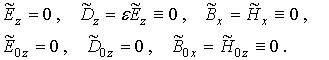 (22)
(22)
Формулы (20) позволяют написать далее
Аналогичные соотношения при замене в (23) e на единицу получаются для компонент поля в вакууме.
Наряду с равенствами (23) из выражений (20) следует с учетом (22), что
![]() . (24)
. (24)
В уравнениях
(24) компоненты ![]() и
и
![]() попарно
связываются между собой и, как нетрудно видеть, удовлетворяются при
попарно
связываются между собой и, как нетрудно видеть, удовлетворяются при ![]() (
(![]() ) только при наложении условий Ez=0, Bx=0,
) только при наложении условий Ez=0, Bx=0, ![]() . Это означает, что в лабораторной системе
отсчета ортогональность электрического и магнитного полей волны выполняется при
сохранении параллельности магнитного поля оси z и компланарности векторов
. Это означает, что в лабораторной системе
отсчета ортогональность электрического и магнитного полей волны выполняется при
сохранении параллельности магнитного поля оси z и компланарности векторов ![]() и
и ![]() плоскости движения слоя.
Аналогичная особенность из-за необходимости соблюдения соотношений типа (24)
при b<1 имеет силу и за пределами слоя. Таким
образом, переход в лабораторную систему отсчета не меняет поляризацию ТМ-волны.
плоскости движения слоя.
Аналогичная особенность из-за необходимости соблюдения соотношений типа (24)
при b<1 имеет силу и за пределами слоя. Таким
образом, переход в лабораторную систему отсчета не меняет поляризацию ТМ-волны.
Если из уравнений (23) для ![]() и
и ![]() исключить
исключить ![]() , то получим продольную компоненту
электрического поля
, то получим продольную компоненту
электрического поля
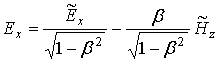 . (25)
. (25)
Аналогичным
образом, исключая из оставшихся выражений (23) ![]() , найдем
, найдем
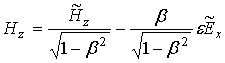 . (26)
. (26)
Для выражения величин ![]() и
и ![]() следует воспользоваться вытекающими из
системы (23) равенствами
следует воспользоваться вытекающими из
системы (23) равенствами ![]() .
.
Исключая вначале ![]() , получим
, получим
а затем найдем
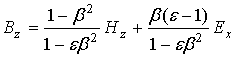 . (28)
. (28)
Соответствующие
представления компонент поля в вакууме получаются из выражений (25)-(28), если
положить ![]() .
.
Формулы (25)-(28) вместе с равенствами (21) позволяют выразить компоненты полей лабораторной системы через компоненты попутной системы отсчета, которые заданы равенствами (11), (12) и согласно (8) определяют компоненты электрических полей. Имеем в итоге следующие выражения для ненулевых компонент полей плазмы в лабораторной системе отсчета
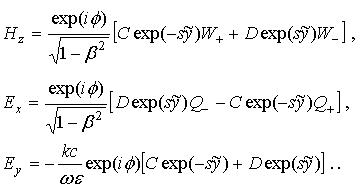 (29)
(29)
Здесь обозначено
![]() . (30)
. (30)
Для полей в вакууме (вне слоя) в силу равенств (25)-(28) при e=1, согласно (12) и следующим из уравнений (8) для вакуума связям компонент полей имеем в лабораторной системе отсчета представления
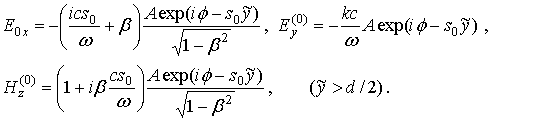 (31)
(31)
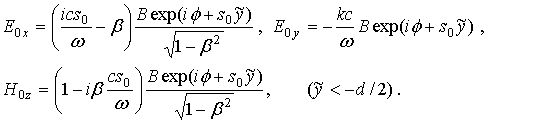 (32)
(32)
Для
окончательной записи полей в лабораторной системе отсчета в выражениях (29),
(31), (32) остается преобразовать фазу колебаний ![]() и заменить
и заменить ![]() согласно (18). Видно, что в преобразованной форме колебания
всех компонент полей описываются в лабораторной системе отсчета экспонентой
согласно (18). Видно, что в преобразованной форме колебания
всех компонент полей описываются в лабораторной системе отсчета экспонентой ![]() , где
, где
Равенства (33) показывают, что в лабораторной системе отсчета имеет место
доплеровское приращение частоты регистрируемых колебаний. Наряду с этим
образуется поперечная составляющая p волнового вектора ![]() (
(![]() ) поверхностной волны, характеризующая
поворот волновой нормали в сторону движения слоя. Таким образом, поверхностная
волна оказывается неколлинеарной поверхностной волной. Существенно, впрочем,
что в отличие от неколлинеарных поверхностных волн на нерелятивистских границах
[2-4] она неколлинеарна только с позиции наблюдателя в лабораторной системе
отсчета. Иначе говоря, ее неколлинеарность – в чистом виде аберрационный
эффект, обязанный сносу волны движущимся слоем.
) поверхностной волны, характеризующая
поворот волновой нормали в сторону движения слоя. Таким образом, поверхностная
волна оказывается неколлинеарной поверхностной волной. Существенно, впрочем,
что в отличие от неколлинеарных поверхностных волн на нерелятивистских границах
[2-4] она неколлинеарна только с позиции наблюдателя в лабораторной системе
отсчета. Иначе говоря, ее неколлинеарность – в чистом виде аберрационный
эффект, обязанный сносу волны движущимся слоем.
Спадание полей в стороны от границ слоя движущейся плазмы выразится
множителями ![]() и
и ![]() . Здесь, конечно,
. Здесь, конечно, ![]() должно быть заменено
согласно (18). Соответственно получим
должно быть заменено
согласно (18). Соответственно получим
![]() ,
, ![]() ,
,
где в
областях определения полей лабораторной системы отсчета разности ![]() всегда положительны.
Величины
всегда положительны.
Величины
![]() (34)
(34)
есть коэффициенты граничной локализации полей в плазме и в вакууме с позиции наблюдателя лабораторной системы отсчета. Из (34) видно, что движение слоя способствует повышению локализации полей на его границах, – результат, представляющий следствие релятивистского сокращения размеров по направлению движения слоя.
Спектры мод в лабораторной системе отсчета
Для завершения описания свойств поверхностной ТМ-волны, удерживаемой релятивистски движущимся слоем плазмы, необходимо рассмотреть особенности спектрального поведения мод с точки зрения наблюдателя лабораторной системы отсчета. Представление в ней дисперсионных спектров естественно получить, подвергнув релятивистскому преобразованию дисперсионное соотношение (16) или (17). Релятивистская инвариантность k и формулы (34) обеспечивают переход к спектрам лабораторной системы отсчета заменой: k®k, s®G(1-b2)1/2, s0®G0(1-b2)1/2. Остается определиться с преобразованием диэлектрической проницаемости плазмы.
Согласно общеизвестному факту релятивистского превращения движущейся среды с частотной дисперсией в среду, демонстрирующую еще и пространственную дисперсию [9] следует ожидать, что диэлектрическая проницаемость будет преобразовываться при переходе в лабораторную систему отсчета по схеме
Ввиду (36) дисперсионное соотношение (16) примет в лабораторной системе отсчета вид
Важно подчеркнуть, что если даже в (36) фиксировать ![]() , зависимость
, зависимость ![]() вовсе не обязана воспроизводить
зависимость e(w) в формате
связи частот равенством (33). По этой причине, чтобы установить преобразование
(36), обратимся к исходному определению величин e и e¢ как показателей поляризационного отклика среды, связующих электрические
индукции и напряженности полей. Предварительно заметим, что в рамках
элементарного подхода к описанию плазмы индуцированную ее движением
пространственную дисперсию уместнее трактовать как специфическую разновидность
оптической анизотропии.
вовсе не обязана воспроизводить
зависимость e(w) в формате
связи частот равенством (33). По этой причине, чтобы установить преобразование
(36), обратимся к исходному определению величин e и e¢ как показателей поляризационного отклика среды, связующих электрические
индукции и напряженности полей. Предварительно заметим, что в рамках
элементарного подхода к описанию плазмы индуцированную ее движением
пространственную дисперсию уместнее трактовать как специфическую разновидность
оптической анизотропии.
В лабораторной системе отсчета, как видно из соотношений (21), величина e продолжает выступать в своем
качестве только по отношению к составляющим электрического поля Ey и Dy. Напротив, это качество она теряет с
переходом в лабораторную систему отсчета по отношению к компонентам
электрических полей, направленным поперек движения плазмы. Чтобы удостоверится
в этом факте достаточно сравнить выражение для величины ![]() из (23) с формулой (27).
из (23) с формулой (27).
На основании изложенного для составляющих индукции электрического поля
напишем ![]() .
Несовпадение e и e¢ в этих равенствах, по сути
вытекающее из различного характера релятивистского преобразования продольных и
поперечных компонент полей (см. формулы (19), (20)), служит типичным признаком
оптической анизотропии среды в лабораторной системе отсчета. Выражение для Dx не противоречит (27), если принять
пропорциональность величин Hz и Ex. Первое слагаемое в (27)
представляет, таким образом, релятивистский вклад магнитного поля в поперечную
поляризуемость плазмы. В области существования поверхностной ТМ-волны e<1 и чтобы указанный вклад в
поляризуемость был положительным, примем
.
Несовпадение e и e¢ в этих равенствах, по сути
вытекающее из различного характера релятивистского преобразования продольных и
поперечных компонент полей (см. формулы (19), (20)), служит типичным признаком
оптической анизотропии среды в лабораторной системе отсчета. Выражение для Dx не противоречит (27), если принять
пропорциональность величин Hz и Ex. Первое слагаемое в (27)
представляет, таким образом, релятивистский вклад магнитного поля в поперечную
поляризуемость плазмы. В области существования поверхностной ТМ-волны e<1 и чтобы указанный вклад в
поляризуемость был положительным, примем
![]() . (38)
. (38)
Подстановка Hz из (38) в (27) сразу приводит к равенству
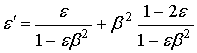 , (39)
, (39)
устанавливающему вид преобразования (36). Аналогичный результат был получен в [5] для полубесконечной плазмы непосредственно из решения граничной задачи с импедансными граничными условиями, подразумевающими непрерывность тангенциальных составляющих напряженностей полей. Как указывалось Островским [11], если скорость границы не является в точности световой (b¹1), именно непрерывность полей, как следствие инерционного отклика движущейся среды на скачкообразное изменение ее характеристик в точках резкой границы, выступает общим правилом поведения. Фактически, это не противоречит стандартным релятивистским граничным условиям [9], из которых данная непрерывность компонент полей вытекает как более жесткое условие на отбор решения вследствие принятой геометричности границы. Итак, в лабораторной системе отсчета дисперсионные спектры мод поверхностной ТМ-волны, удерживаемой границами релятивистски движущегося слоя плазмы, можно получить как совместное решение уравнений (37), (39) с учетом равенств (13) и следующей из них связи величин s и s0.
Если ввести безразмерные спектральные переменные s=Gd, s0=G0d, уравнению (37) можно придать вид
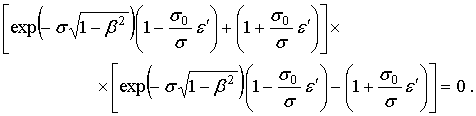 (40)
(40)
Как и в попутной системе отсчета, дисперсионные спектры поверхностной ТМ-волны представлены двумя модами. Каждой из них соответствует дисперсионное соотношение в виде независимого равенства нулю сомножителей, содержащихся в (40) в квадратных скобках. Из них можно выразить e¢, а затем, используя (39), определить в явном виде частоту. В результате указанных преобразований получим
где с учетом (34) обозначено
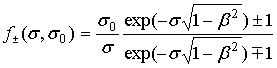 ,
, 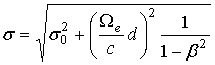 . (42)
. (42)
Формула (41) может, поэтому, рассматриваться как явная функциональная зависимость частоты спектра моды W от приведенного коэффициента граничной локализации ее полей при спадании в плазму s или вакуум s0. Остальные спектральные показатели мод легко пересчитываются по избранному, например, значению s0 и найденным по формулам (41), (42) значениям W и s. Так, приведенное волновое число c=kd можно рассчитать далее по второму из соотношений (13). Ввиду связи частот (33) оно дает:
Выражения (41)-(43),
ко всему прочему, показывают, что варьируемыми параметрами спектров выступает
релятивистский фактор ![]() и
комбинированный показатель плазменного слоя a=Wed/c.
и
комбинированный показатель плазменного слоя a=Wed/c.
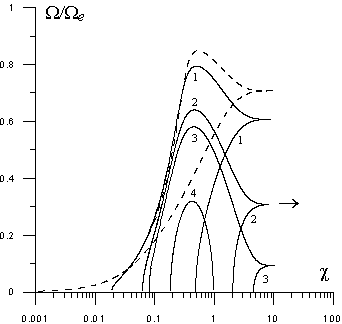
Расчет дисперсионных спектров по формулам (41)-(43) не вызывает трудностей. Основными спектральными зависимостями условимся рассматривать зависимости s0=s0(W) и W=W(c). Наибольший интерес представляет случай, когда Wec/d<0.73 и антисимметричная мода является обратной волной [8]. На рис. 2 показаны спектры мод, отвечающие этому условию. Штриховые кривые соответствуют неподвижному (b=0) слою, а сплошные – движущемуся слою и пронумерованы в порядке возрастания его скорости.
При малых скоростях слоя (b<<1) изменения дисперсионных спектров выражены чрезвычайно слабо. В этой связи расчет спектров мод выполнен, начиная с умеренных значений b<1. Аналогично статичному слою, спектр мод движущегося слоя образуется двумя ветвями, которые сливаются в горизонтальную прямую (продолжение ее показано для кривых 2 стрелкой), представляющую коротковолновую асимптоту спектра. Та из ветвей, что лежит ниже этой асимптоты, представляет симметричную моду поверхностной ТМ-волны. Ветвь антисимметричной моды вначале круто поднимается над асимптотой, а затем, пройдя максимум, опускается к ней.
|
|
|
|
|
|
Рис. 2. Дисперсионные спектры поверхностной ТМ-волны в лабораторной системе отсчета: Wed/c=0.4, 1 – b=0.4, 2 – b=0.55, 3 – b=0.575, 4 – b=0.63. |
|
Выходу на асимптотический уровень спектра мод в условиях релятивистского движения слоя соответствует переход к пределу d®¥ в дисперсионном соотношении (37). Именно этот случай полубесконечной плазмы рассматривался в работе [5]. Наряду с понижением уровня асимптот по мере роста b, что наглядно демонстрируют кривые рис. 2, в [5] отмечалось также обрезание ветвей спектра со стороны длинноволновой его части. Этот результат объяснялся следствием неразрывной связи пространства-времени в условиях релятивистского движения плазмы: частотная отсечка спектра (ограничение спектра по временнóму фактору, выраженное образованием коротковолновой асимптоты) влечет в релятивистских условиях отсечку спектра со стороны длинных волн (вступает в действие ограничение спектра и по пространственному фактору).
Для полубесконечной плазмы, как и в коротковолновом пределе, различие между симметричной и антисимметричной модами слоя пропадает. Поэтому спектры работы [5] получатся из спектров рис.2, если отбросить “дублирующие” ветви антисимметричной моды[1]. Кривая 4, относящаяся целиком к антисимметричной моде, будет отсутствовать, а сохранившиеся ветви 1-3 симметричной моды дадут в итоге картину, которая представлена в [5] на втором рисунке.
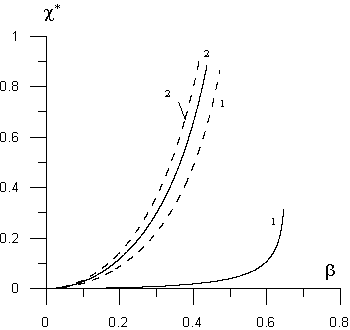
Наличие нижней, релятивистской границы спектра по волновому числу c, как видно из рис. 2, сохраняется и при конечной толщине слоя плазмы. Качественное отличие от случая полубесконечной плазмы состоит в том, что существует режим релятивистского движения слоя, при котором симметричная мода отсекается полностью и не воспринимается наблюдателем в лабораторной системе отсчета, тогда как антисимметричная мода (см. кривую 4) сохраняется в спектре своей вершинной частью. В точках релятивистской границы спектра c=c* имеем W=0. Поэтому, в соответствии с (41) для определения c* требуется численно решить трансцендентные уравнения
![]() , (44)
, (44)
где предварительно следует выразить s через s0. Найденные так с учетом формулы (43) значения c*=(1-b2)1/2 s0, будут неодинаковыми для симметричной и антисимметричной мод из-за неравенства f+ (s,s0)¹ f-(s,s0). Типичные зависимости c* от b представлены на рис. 3, где штриховыми кривыми показаны изменения релятивистской границы спектра для симметричной моды. Сплошные кривые, лежащие всегда ниже штриховых кривых, представляют здесь зависимости c*(b) для антисимметричной моды. Сравнение кривых позволяет заключить, что для плотной плазмы слоя (кривые 2) различие в релятивистских границах спектра симметричных и антисимметричных мод выражено заметно слабее, чем в случае "рыхлой" плазмы (кривые 1).
|
|
|
|
|
|
Рис.3. Зависимости волновых чисел релятивистской отсечки спектра мод поверхностных ТМ-волн от b: 1 – Wed/c=0.4, 2 – Wed/c=3. |
|
Для полноты описания мод в лабораторной системе отсчета кривым дисперсии рис.2 полезно сопоставить частотные зависимости коэффициента s0. Они получаются непосредственно численным обращением уравнений (41), демонстрируя качественное сходство с кривыми дисперсии рис. 2. Соответствующую картину можно представить, если на рис. 2 поменять местами горизонтальную и вертикальную оси, а затем заменить c на s0. Из нее следует, что при отсутствии движения слоя (b=0, штриховые кривые) в пределе W®0 происходит полная делокализация колебаний вне слоя. Для движущегося слоя плазмы (сплошные кривые 1-4) этому препятствует релятивистская отсечка спектра по волновому числу. В коротковолновом асимптотическом пределе спектров имеет место неограниченный рост локализуемости колебаний обеих мод, а на частотах ниже частоты коротковолнового асимптотического предела, где возможно сосуществование симметричной и антисимметричной мод, локализуемость полей антисимметричной моды в вакууме всегда ниже, чем у симметричной моды.
Выводы
В работе исследовано поведение мод поверхностных ТМ-волн на границах релятивистски движущегося слоя плазмы. Показано, что при переходе в лабораторную систему отсчета поверхностная ТМ-волна вместе с доплеровским повышением частоты претерпевает поворот волновой нормали в сторону движения слоя и становится неколлинеарной поверхностной волной. Установлено, что линейные релятивистские вклады электрического и магнитного полей в поляризуемость плазмы вдоль слоя добавляют в спектре мод к частотной отсечке релятивистскую отсечку по волновому числу. Последнее интерпретируется как проявление релятивистской неразрывности пространства-времени.
Отмечается, что из-за релятивистского сокращения размеров по направлению движения слоя граничная локализация полей мод повышается. Показано, что существуют такие режимы релятивистского движения плазмы, когда наблюдатель в лабораторной системе отсчета воспринимает колебания только антисимметричной моды с частотами выше частоты отсечки спектра.
Литература
1. Ерохин Н.С., Кузелев М.В, Моисеев С.С. и др. Неравновесные и резонансные процессы в плазменной радиофизике. М.: Наука, 1982.
2. Шевяхов Н.С. // Письма в ЖТФ. 2002. Т. 28. № 12. С. 40.
3. Гуляев Ю.В., Колчина Г.А., Шавров В.Г., Шевяхов Н.С. // РЭ. 2003. Т. 48. № 4. С. 459.
4. Колчина Г.А., Неганов В.А., Шевяхов Н.С. // Физика волновых процессов и радиотехнические системы. 2004. Т. 7. № 2. С. 19.
5. Марышев С.Н., Шевяхов Н.С.. // Письма в ЖТФ. 2004. Т. 30. № 23. С. 40.
6. Аскарьян Г.А., Манзон Б.М. // Письма в ЖЭТФ. 1980. Т. 31. № 5. С. 283.
7. Красильников В.Н. Параметрические волновые явления в классической электродинамике. С.-Пб: Изд-во СПб Университета, 1996.
8. Кондратенко А.Н. Поверхностные и объемные волны в ограниченной плазме. М.: Энергоатомиздат, 1985.
9. Бредов М.М., Румянцев В.В., Топтыгин И.Н. Классическая электродинамика.
М.: Наука, 1985.
10. Паули В. Теория относительности. М.: Наука, 1983.
11. Островский Л.А. // УФН. 1975. Т. 116. № 2. С. 313.
[1] Полагая предельный переход d®¥ уже свершившимся и ветви антисимметричной моды сколь угодно приблизившимися к соответствующим ветвям симметричной моды, под спектральной переменной c следует теперь понимать волновое число k, нормированное на какое-либо характерное его значение, например, на We/c.
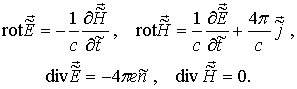 (1)
(1)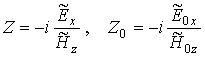 .
(5)
.
(5)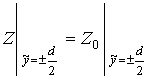 . (6)
. (6)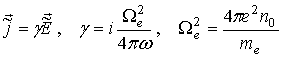 , (7)
, (7)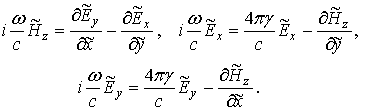 (8)
(8)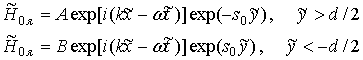 . (12)
. (12)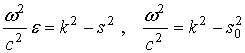 . (13)
. (13)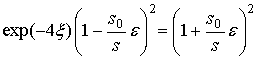 . (16)
. (16)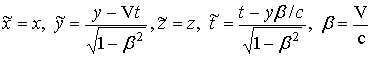
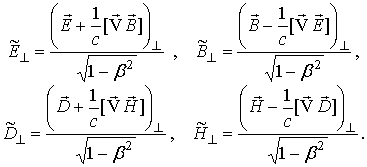
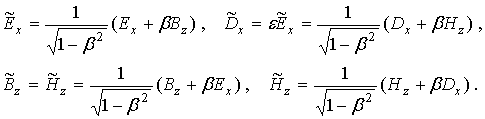 (23)
(23)
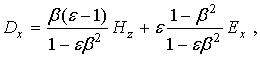 (27)
(27)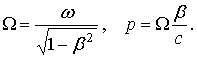 (33)
(33)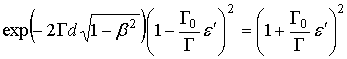 . (37)
. (37)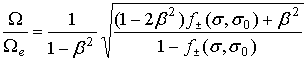 , (41)
, (41)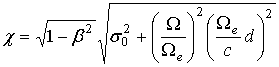 . (43)
. (43)