УДК 621.396.67.01
ХАРАКТЕРИСТИКИ РАССЕЯНИЯ ПЛОСКОЙ ВИБРАТОРНОЙ РЕШЁТКИ ФАЗОВОЙ МОНОИМПУЛЬСНОЙ СИСТЕМЫ [*]
Б. Д. Мануилов 1, А. А. Кузнецов 2
1Федеральное государственное унитарное предприятие «Ростовский-на-Дону научно-исследовательский институт радиосвязи», г. Ростов-на-Дону
2Ростовский технологический институт сервиса и туризма (филиал) ФГОУ ВПО «Южно-российский государственный университет экономики и сервиса»,
г. Ростов-на-Дону
Получена 11 января 2013 г.
Аннотация. С использованием аппарата матриц рассеяния получены выражения для структурной и антенных составляющих полей двухпозиционного рассеяния плоской решётки вибраторов фазовой моноимпульсной системы. Учтена схема возбуждения решётки, состоящая из суммарно-разностного преобразователя и четырёх формирующих многополюсников с фазовращателями в каналах излучателей. Матрица рассеяния входов вибраторов найдена через их матрицу сопротивлений, для определения которой применён метод наведённых ЭДС. На основе энергетического подхода, применявшегося ранее к задачам рассеяния Л.И. Пономарёвым, получены оценки различных составляющих эффективной площади рассеяния (ЭПР). Приведены объёмные диаграммы направленности рассеянного поля и максимальные значения компонент ЭПР для плоской решётки из 144-х вибраторов.
Ключевые слова: антенная решетка, фазовая моноимпульсная система, диаграмма направленности рассеянного поля.
Abstract: The expressions for structural and antenna components of two-position scattering field of plane array of dipoles of phase monopulse system are obtained on the base of scattering matrix technique. The scheme of excitement of array consists of four forming multiterminal networks with phase shifters in channels of radiators and the total and differential converter. The matrix of dispersion of entrances of vibrators is found through their matrix of resistance which is determined by a method of induced EDS. Estimates of various components of the effective area of dispersion (EAD) are received on the basis of power approach (L.I. Ponomarev applied earlier to problems of dispersion). Volume directional patterns of a scattered field and the maximum values the EAD component for a array from 144 vibrators are provided in the report.
Key words: antenna array, phase monopulse system, directional patterns of a scattered field.
Учёт характеристик рассеяния антенн важен как для оценки радиолокационной заметности объектов, так и для решения вопросов электромагнитной совместимости систем. В известных работах, посвящённых характеристикам рассеяния антенн (см. например, [1-6]), рассмотрены многие фундаментальные вопросы, связанные с соотношением мощностей, принимаемых и рассеиваемых антеннами и антенными решётками (АР), со структурой полей рассеяния и методами их расчёта, с интегральными и дифференциальными поперечниками рассеяния, с синтезом антенн с заданными рассеивающими свойствами и ряд других. В частности, в работе [7] рассмотрены особенности характеристик рассеяния плоских вибраторных АР при формировании ими многолепестковых диаграмм направленности (ДН). Однако в известных работах не исследовались характеристики рассеяния моноимпульсных АР, хотя моноимпульсные методы автосопровождения в настоящее время широко применяются не только в радиолокации, но и в системах связи с летательными аппаратами. При этом моноимпульсная АР формирует суммарную и две разностных диаграммы направленности (ДН).
Целью работы является анализ диаграмм направленности структурной и антенных составляющих рассеянного поля и дифференциальной эффективной площади двухпозиционного рассеяния плоских вибраторных АР конечных размеров для фазовых моноимпульсных систем.
Для определения ДН структурной и антенных составляющих поля рассеяния с учётом схемы возбуждения излучателей в статье применен аппарат матриц рассеяния, разработанный Д.М. Сазоновым [2].
В идейном плане статья является развитием работы [7], в которой аналогичная задача решалась для плоской решётки вибраторов, формирующей многолепестковую диаграмму направленности.
Схематически структура
излучающей системы представлена на рис. 1. Цифрами 0, I и II обозначены
соответственно суммарно-разностный преобразователь, формирующий многополюсник и
антенное полотно. Греческими буквами обозначены соответствующие сечения входов
системы, причём входы ![]() соответствуют дальней зоне АР.
На входах системы обозначены также нормированные напряжения падающих и
отражённых волн.
соответствуют дальней зоне АР.
На входах системы обозначены также нормированные напряжения падающих и
отражённых волн.
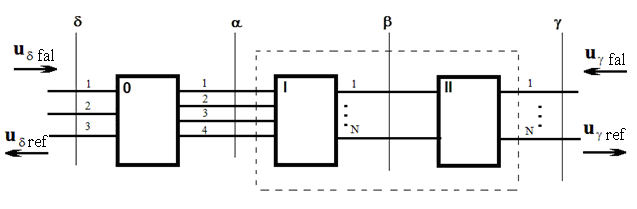
Рис. 1. К построению матрицы рассеяния АР для фазовой моноимпульсной системы
АР состоит из ![]() вибраторов,
расположенных в узлах квадратной сетки с шагом d над бесконечным
проводящим экраном (
вибраторов,
расположенных в узлах квадратной сетки с шагом d над бесконечным
проводящим экраном (![]() ) на высоте
) на высоте ![]() и ориентированных вдоль оси 0y.
и ориентированных вдоль оси 0y.
Излучатели каждого из
четырёх квадрантов соединены с соответствующим входом формирующего многополюсника
и далее через комплексные взвешивающие устройства ![]()
![]() либо
только фазовращатели соединены со своим распределителем (сумматором). Последний
в свою очередь подсоединен к одному из четырёх входов суммарно-разностного преобразователя,
формирующего суммарную и две разностные диаграммы направленности.
либо
только фазовращатели соединены со своим распределителем (сумматором). Последний
в свою очередь подсоединен к одному из четырёх входов суммарно-разностного преобразователя,
формирующего суммарную и две разностные диаграммы направленности.
Будем искать структурную и антенные составляющие полей рассеяния.
Матрица рассеяния ![]() антенной системы может быть найдена путём
объединения матриц рассеяния суммарно-разностного преобразователя (
антенной системы может быть найдена путём
объединения матриц рассеяния суммарно-разностного преобразователя (![]() ), формирующего многополюсника (
), формирующего многополюсника (![]() ) и антенного полотна (
) и антенного полотна (![]() ):
):
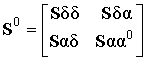 ,
, 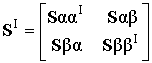 и
и 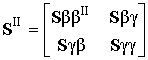 . (1)
. (1)
Индексами ![]() ,
, ![]() ,
, ![]() , и
, и ![]() обозначены соответственно 3 входа
суммарно-разностного преобразователя, 4 входа формирующего многополюсника,
обозначены соответственно 3 входа
суммарно-разностного преобразователя, 4 входа формирующего многополюсника, ![]() входов, соединяющих этот многополюсник с
антенным полотном, и
входов, соединяющих этот многополюсник с
антенным полотном, и ![]() выходов антенного полотна. Под
выходами последнего будем понимать
выходов антенного полотна. Под
выходами последнего будем понимать ![]() ортогональных
парциальных характеристик направленности.
ортогональных
парциальных характеристик направленности.
Элементы блочных матриц
![]() ,
, ![]() ,
, ![]() являются квадратными матрицами размера
являются квадратными матрицами размера ![]() , за исключением матриц
, за исключением матриц ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Перейдём к
конкретизации элементов матриц рассеяния ![]() ,
, ![]() ,
, ![]() .
.
Если
суммарно-разностный преобразователь выполнен на четырёх согласованных кольцевых
мостах без потерь, то диагональные блоки ![]() -
нулевые, а недиагональные определяются соотношениями:
-
нулевые, а недиагональные определяются соотношениями:
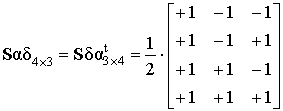 . (2)
. (2)
Первый столбец в (2) соответствует суммарному каналу, а два остальных – разностным; t – знак транспонирования матрицы.
Полагая, что входящий в
состав формирующего многополюсника высокочастотный сумматор обеспечивает
равномерное распределение мощности, поступающей на каждый из четырёх входов ![]() , между соответствующими
, между соответствующими ![]() входами, представим элементы идеальной
матрицы рассеяния формирующего
входами, представим элементы идеальной
матрицы рассеяния формирующего ![]() – полюсника в
следующем виде:
– полюсника в
следующем виде:
 ,
(3)
,
(3)
 ,
(4)
,
(4)
![]() ,
, ![]() , (5)
, (5)
Здесь ![]() -
нулевая матрица размера
-
нулевая матрица размера ![]() /4.
/4.
Отличные от нуля
элементы матрицы ![]() имеют вид:
имеют вид:
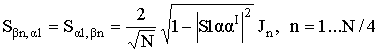 ,
,
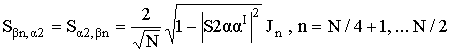 ,
,
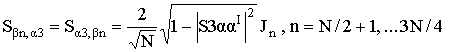 ,
,
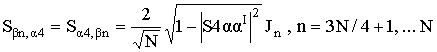 . (6)
. (6)
Матрица ![]() связывает
векторы нормированных напряжений падающих (fal)
и отражённых (ref)
волн как на входах вибраторов (
связывает
векторы нормированных напряжений падающих (fal)
и отражённых (ref)
волн как на входах вибраторов (![]() ), так и в пространстве
(
), так и в пространстве
(![]() ):
):
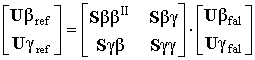 .
(7)
.
(7)
Используя результаты работы [2],
запишем выражения для блоков матрицы ![]() :
:
![]() ;
(8)
;
(8)
![]() ;
(9)
;
(9)
![]() ;
(10)
;
(10)
![]() .
(11)
.
(11)
Здесь ![]() -знак
комплексного сопряжения,
-знак
комплексного сопряжения, ![]() - единичная матрица,
- единичная матрица, ![]() означает матрицу нормированных
сопротивлений входов вибраторов. Матрица сопротивлений вибраторной АР найдена
методом наведённых ЭДС с использованием функции Грина полупространства. Через
означает матрицу нормированных
сопротивлений входов вибраторов. Матрица сопротивлений вибраторной АР найдена
методом наведённых ЭДС с использованием функции Грина полупространства. Через ![]() обозначена так называемая
ортогонализующая матрица токов [2]
обозначена так называемая
ортогонализующая матрица токов [2]
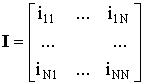 , (12)
, (12)
каждому столбцу которой соответствует
одна из ![]() ортонормированных характеристик
направленности решётки
ортонормированных характеристик
направленности решётки ![]() :
:
![]() , или
, или
![]() . (13)
. (13)
Через ![]() обозначена
ДН изолированного элемента. Углы
обозначена
ДН изолированного элемента. Углы ![]() отсчитываются от
положительных направлений осей x
и y. Вид ортогонализующей
матрицы токов не принципиален, так как она в конечных выражениях отсутствует.
отсчитываются от
положительных направлений осей x
и y. Вид ортогонализующей
матрицы токов не принципиален, так как она в конечных выражениях отсутствует.
Определив блоки матриц ![]() ,
, ![]() ,
, ![]() , перейдём к построению математической
модели данной антенной системы, конкретизируя вид матрицы рассеяния всей
решётки как 2(N+3)-полюсника, применив
формулы объединения каскадно соединённых многополюсников. В итоге получим:
, перейдём к построению математической
модели данной антенной системы, конкретизируя вид матрицы рассеяния всей
решётки как 2(N+3)-полюсника, применив
формулы объединения каскадно соединённых многополюсников. В итоге получим:
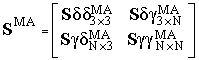 . (14)
. (14)
Входящие в (14) блочные матрицы описываются выражениями:
![]() , (15)
, (15)
![]() , (16)
, (16)
![]() , (17)
, (17)
Верхним индексом ![]() в (15)–(18) обозначены блоки объединённой
матрицы рассеяния антенного полотна и формирующего многополюсника, обведённых
на рис. 1 штриховой линией. Их структура приведена в [7]. Небольшие отличия
обусловлены увеличением числа входов формирующего многополюсника. Матрица
в (15)–(18) обозначены блоки объединённой
матрицы рассеяния антенного полотна и формирующего многополюсника, обведённых
на рис. 1 штриховой линией. Их структура приведена в [7]. Небольшие отличия
обусловлены увеличением числа входов формирующего многополюсника. Матрица ![]() - единичная.
- единичная.
Если приемники соответствующих каналов не согласованы с выходами суммарно-разностного преобразователя, то векторы нормированных напряжений падающих (по отношению к решётке) и отражённых волн связаны диагональной матрицей коэффициентов отражения:
![]() . (19)
. (19)
С учётом этого для вектора нормированных напряжений волн, рассеянных решёткой в режиме приёма, можно получить:
![]() . (20)
. (20)
Из (20) видно, что
рассеянное поле можно разделить, как это принято, на две составляющие. Второе
слагаемое определяет так называемые антенные (зависящие от нагрузки)
составляющие. Здесь фигурируют как N входов γ, относящиеся к
дальней зоне, так и 3 входа δ, относящиеся ко входам приёмников. В
случае согласования фидеров с выходами суммарно-разностного преобразователя и
приёмниками матрица ![]() становится нулевой и антенные
составляющие рассеянного поля обращаются в нуль. Обратимся к первому слагаемому
в (20), вид которого определён выражением (18). Здесь не фигурируют входы
приёмников δ, то есть оно не зависит от нагрузки. Тем не менее оно
зависит от структуры АР, причём матрицы
становится нулевой и антенные
составляющие рассеянного поля обращаются в нуль. Обратимся к первому слагаемому
в (20), вид которого определён выражением (18). Здесь не фигурируют входы
приёмников δ, то есть оно не зависит от нагрузки. Тем не менее оно
зависит от структуры АР, причём матрицы ![]() и
и ![]() содержат информацию о состояниях
фазовращателей и других устройств. Чаще всего эти составляющие рассеянного поля
называют структурными. Однако заметим, что в последние годы появились и другие
названия. В книге Пономарёва Л.И. и Попова В.В. [3], изданной в 2003 г., применено название «оболочка» антенны. В книге Бина Манка [4], изданной в том же году,
используется название «остаточная составляющая». Тем не менее, в справочнике
Константина Баланиса [5], изданном в 2008 г., используется традиционное название. Мы также будем использовать это название.
содержат информацию о состояниях
фазовращателей и других устройств. Чаще всего эти составляющие рассеянного поля
называют структурными. Однако заметим, что в последние годы появились и другие
названия. В книге Пономарёва Л.И. и Попова В.В. [3], изданной в 2003 г., применено название «оболочка» антенны. В книге Бина Манка [4], изданной в том же году,
используется название «остаточная составляющая». Тем не менее, в справочнике
Константина Баланиса [5], изданном в 2008 г., используется традиционное название. Мы также будем использовать это название.
Для диаграмм направленности структурной (res) и антенных (ant) составляющих рассеянного поля получены следующие представления:
![]() .
(22)
.
(22)
Через ![]() обозначен вектор-столбец ДН
элементов АР,
обозначен вектор-столбец ДН
элементов АР, ![]() обозначает
вектор-столбец из ЭДС холостого хода на входах вибраторов при падении на
решётку плоской волны с направления
обозначает
вектор-столбец из ЭДС холостого хода на входах вибраторов при падении на
решётку плоской волны с направления ![]() [2]. Диагональная
матрица
[2]. Диагональная
матрица ![]() содержит информацию о
коэффициентах отражения от трёх приёмников. Выражение (22) является
суперпозицией трёх антенных составляющих поля, рассеянного не согласованной с
приёмниками решёткой.
содержит информацию о
коэффициентах отражения от трёх приёмников. Выражение (22) является
суперпозицией трёх антенных составляющих поля, рассеянного не согласованной с
приёмниками решёткой.
Заметим, что здесь рассмотрение также ограничено так называемой «параллельной» составляющей падающего поля, которая взаимодействует с АР.
Численное моделирование
проведено на равномерно возбуждённой АР, состоящей из ста сорока четырёх (![]() ) вибраторов с радиусом
) вибраторов с радиусом ![]() и длиной плеч
и длиной плеч ![]() при
при ![]() ,
, ![]() (как и
в [7]). Это даёт возможность сравнить формы структурных составляющих полей
рассеяния АР в моноимпульсном и обычном режимах. На рис. 2 представлена в виде
линий уровня нормированная ДН структурной составляющей поля рассеяния
моноимпульсной АР, облучаемой волной перпендикулярной поляризации, падающей с
направления
(как и
в [7]). Это даёт возможность сравнить формы структурных составляющих полей
рассеяния АР в моноимпульсном и обычном режимах. На рис. 2 представлена в виде
линий уровня нормированная ДН структурной составляющей поля рассеяния
моноимпульсной АР, облучаемой волной перпендикулярной поляризации, падающей с
направления ![]() ,
, ![]() . Имеем
полное совпадение с рис. 2 из [7].
. Имеем
полное совпадение с рис. 2 из [7].
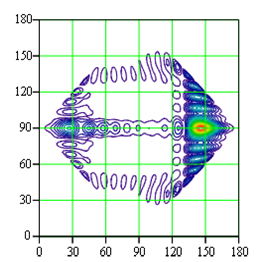
Рис. 2. ДН структурной составляющей поля рассеяния
фазовой моноимпульсной системы при ![]() ,
, ![]()
Из (18) видно, что
полного совпадения не будет, если ![]() , то есть если входы a
суммарно-разностного преобразователя не будут согласованы и развязаны.
Диаграммы направленности суммарной и разностных антенных составляющих поля
рассеяния имеют точно такую же форму, как соответствующие ДН на передачу. Их
уровень зависит от согласования фидеров с соответствующими каналами АР и
приёмниками, а также от уровня той или иной ДН в направлении падающей волны.
, то есть если входы a
суммарно-разностного преобразователя не будут согласованы и развязаны.
Диаграммы направленности суммарной и разностных антенных составляющих поля
рассеяния имеют точно такую же форму, как соответствующие ДН на передачу. Их
уровень зависит от согласования фидеров с соответствующими каналами АР и
приёмниками, а также от уровня той или иной ДН в направлении падающей волны.
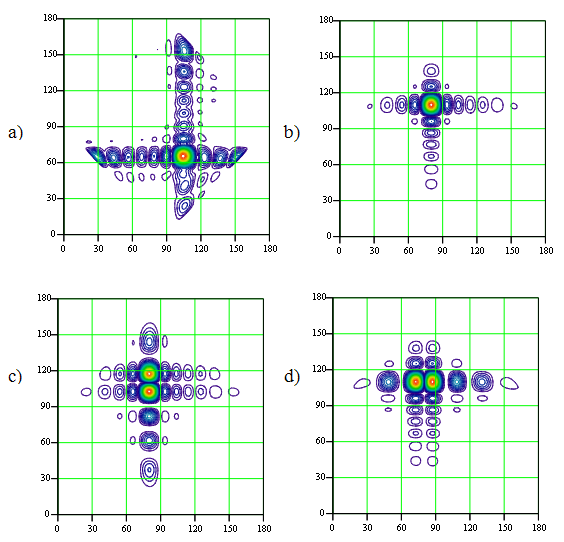
Рис. 3. Диаграммы направленности структурной
составляющей поля рассеяния моно-импульсной АР (а), суммарной (b), разностных
антенных составляющих поля рассеяния по азимуту (c) и по углу
места (d) при ![]() ,
, ![]() ,
, ![]() ,
, ![]()
На рис. 3 приведены ДН
структурной и трех антенных (суммарной и разностных по азимуту и углу места)
составляющих рассеянного поля при падении волны с направления ![]() ,
, ![]() и
ориентации суммарной ДН в направлении
и
ориентации суммарной ДН в направлении ![]() ,
, ![]() . Очевидно, что ДН антенных компонент по форме
идентичны соответствующим ДН фазовой моноимпульсной АР. Суперпозиция ДН трёх
антенных компонент рассеянного поля представлена на рис. 4. В связи с тем, что
разностные ДН рассеянного поля антисимметричны, максимум совокупности антенных
составляющих рассеянного поля оказывается смещён относительно равносигнального
направления. Изображённые на рис. 2-4 диаграммы направленности компонент
рассеянного поля несут информацию лишь об относительном уровне рассеиваемых
полей.
. Очевидно, что ДН антенных компонент по форме
идентичны соответствующим ДН фазовой моноимпульсной АР. Суперпозиция ДН трёх
антенных компонент рассеянного поля представлена на рис. 4. В связи с тем, что
разностные ДН рассеянного поля антисимметричны, максимум совокупности антенных
составляющих рассеянного поля оказывается смещён относительно равносигнального
направления. Изображённые на рис. 2-4 диаграммы направленности компонент
рассеянного поля несут информацию лишь об относительном уровне рассеиваемых
полей.
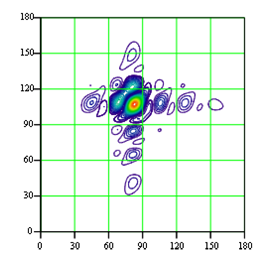
Рис.4. Суперпозиция трёх антенных составляющих рассеянного поля
Для более полной характеристики
рассеивающих свойств линейно поляризованных АР чаще всего применяют скалярную
диаграмму двухпозиционного рассеяния [1], под которой понимают зависимость
дифференциальной (эффективной) поверхности рассеяния решётки ![]() от углов (направления) наблюдения
от углов (направления) наблюдения ![]() при фиксированных углах падения
при фиксированных углах падения ![]() .
.
В работе [7] нами выполнен критический анализ ряда известных представлений для антенных и структурных компонент ЭПР антенных решёток. На основе энергетического метода, применявшегося ранее к задаче рассеяния в работе [3], уточнены содержавшиеся в ряде публикаций выражения для антенных и структурных компонент ЭПР антенных решёток.
Прежде, чем рассматривать структурную составляющую ЭПР решётки для моноимпульсной АР, получим выражения для антенных составляющих ЭПР. Начнём с составляющей, соответствующей суммарному каналу, и воспользуемся определением ЭПР:
где ![]() - расстояние между антенной и РЛС,
- расстояние между антенной и РЛС,
![]() - плотность потока мощности поля вблизи
АР,
- плотность потока мощности поля вблизи
АР,
![]() - плотность потока мощности вблизи РЛС, обусловленная
антенной компонентой суммарного канала.
- плотность потока мощности вблизи РЛС, обусловленная
антенной компонентой суммарного канала.
При падении на решётку
волны с направления ![]() мощность, принятая согласованным
с решёткой приёмником суммарного канала, составляет
мощность, принятая согласованным
с решёткой приёмником суммарного канала, составляет
![]() . (24)
. (24)
Здесь через ![]() обозначен КНД суммарного канала АР с
реальным амплитудно-фазовым распределением (АФР),
обозначен КНД суммарного канала АР с
реальным амплитудно-фазовым распределением (АФР), ![]() - геометрическая
площадь раскрыва,
- геометрическая
площадь раскрыва, ![]() - коэффициент использования
площади раскрыва для суммарного канала,
- коэффициент использования
площади раскрыва для суммарного канала, ![]() - угол,
образуемый равносигнальным направлением с осью z,
- угол,
образуемый равносигнальным направлением с осью z,
![]() – кпд, учитывающий омические потери в
тракте суммарного канала АР,
– кпд, учитывающий омические потери в
тракте суммарного канала АР, ![]() - значение
нормированной ДН суммарного канала в направлении
- значение
нормированной ДН суммарного канала в направлении ![]() ,
, ![]() - скалярное произведение ортов поляризации
поля и антенны. При ориентации вибраторов вдоль оси 0y и использовании поля с
нормальной поляризацией:
- скалярное произведение ортов поляризации
поля и антенны. При ориентации вибраторов вдоль оси 0y и использовании поля с
нормальной поляризацией:
![]() , (25)
, (25)
причём
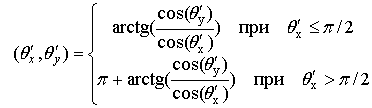 . (26)
. (26)
Доля отражённой от
приёмника суммарного канала мощности определяется квадратом коэффициента
отражения, учитывающим рассогласование фидера с приёмником (![]() ) и решёткой (в режиме передачи
) и решёткой (в режиме передачи ![]() ):
):
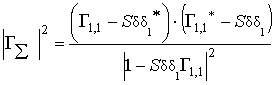 . (27)
. (27)
Плотность потока мощности вблизи РЛС антенной составляющей поля рассеяния, обусловленной рассогласованием тракта суммарного канала, определяется выражением
![]() . (28)
. (28)
Подставив (28) и (24) в (23), получим выражение для антенной составляющей диаграммы двухпозиционного рассеяния, обусловленной рассогласованием тракта суммарного канала
![]() . (29)
. (29)
Аналогично можно получить выражения для двух остальных антенных составляющих диаграммы двухпозиционного рассеяния, обусловленных рассогласованием трактов разностных каналов азимута и угла места:
![]() , (30)
, (30)
![]() . (31)
. (31)
Форма антенных составляющих диаграммы двухпозиционного рассеяния, как это следует из выражений (29) – (31), не зависит от направления падения волны и определяется квадратом соответствующей ДН в режиме передачи.
Для определения структурной составляющей диаграммы двухпозиционного рассеяния в случае АР фазовой моноимпульсной системы применим так называемый энергетический подход [3]. Будем полагать, что мощность плоской волны, проходящей через теневой поперечник антенны, частично поступает на входы приёмников суммарного и разностных каналов, а остальная её часть рассеивается апертурой антенны. При этом с точки зрения структурной составляющей не имеет значения, какая часть поступившей на входы приёмников энергии принимается ими, а какая рассеивается в виде антенных составляющих. После очевидных преобразований можно получить
![]()
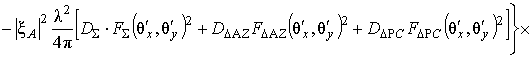
![]() .
(32)
.
(32)
Здесь ![]() и
и ![]()
![]() - нормированная ДН структурной
составляющей двухпозиционного рассеяния и её КНД,
- нормированная ДН структурной
составляющей двухпозиционного рассеяния и её КНД, ![]() - ДН
элемента АР. Сомножители
- ДН
элемента АР. Сомножители ![]() и
и ![]() в первом слагаемом (32) выделяют из
потока мощности через теневой поперечник АР так называемую «параллельную»
составляющую поля, взаимодействующую с АР.
в первом слагаемом (32) выделяют из
потока мощности через теневой поперечник АР так называемую «параллельную»
составляющую поля, взаимодействующую с АР.
Заметим, что под ![]() следует понимать нормированную ДН структурной
составляющей поля рассеяния, определённой выражением (21)
следует понимать нормированную ДН структурной
составляющей поля рассеяния, определённой выражением (21)
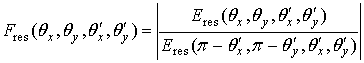 , (33)
, (33)
по которой находится значение КНД ![]() структурной
составляющей рассеянного поля.
структурной
составляющей рассеянного поля.
Из выражения (32)
следует, что форма структурной составляющей диаграммы двухпозиционного
рассеяния ![]() вибраторной АР фазовой
моноимпульсной системы определяется квадратом ДН соответствующей компоненты
рассеянного поля
вибраторной АР фазовой
моноимпульсной системы определяется квадратом ДН соответствующей компоненты
рассеянного поля ![]() . Форма же последней зависит как
от направления наблюдения, так и от направления падения волны. Уменьшение доли
мощности падающей волны, принимаемой каналами АР, автоматически увеличивает
долю структурной компоненты ЭПР.
. Форма же последней зависит как
от направления наблюдения, так и от направления падения волны. Уменьшение доли
мощности падающей волны, принимаемой каналами АР, автоматически увеличивает
долю структурной компоненты ЭПР.
Тестирование
проводилось путём сравнения ЭПР синфазной равномерно возбуждённой АР с ЭПР
металлической пластины при нормальном падении волны, то есть при ![]() ,
, ![]() . При
отсутствии потерь в каналах АР (
. При
отсутствии потерь в каналах АР (![]() =1), согласовании
поляризации падающего поля с ориентацией вибраторов (
=1), согласовании
поляризации падающего поля с ориентацией вибраторов (![]() )
и коротком замыкании выходов суммарного и разностных каналов (
)
и коротком замыкании выходов суммарного и разностных каналов (![]() ) совокупность различных составляющих ЭПР
решётки должна быть близка к ЭПР пластины. Расчёт дал следующие значения максимальных
величин антенных компонент ЭПР:
) совокупность различных составляющих ЭПР
решётки должна быть близка к ЭПР пластины. Расчёт дал следующие значения максимальных
величин антенных компонент ЭПР: ![]() ,
, ![]() ,
,
![]() (здесь
фигурирует та длина волны, в которой заданы размеры АР). На долю структурной
составляющей рассеянного поля при этом приходится ЭПР
(здесь
фигурирует та длина волны, в которой заданы размеры АР). На долю структурной
составляющей рассеянного поля при этом приходится ЭПР ![]() .
ЭПР пластины с размерами АР составляет
.
ЭПР пластины с размерами АР составляет ![]() , что
свидетельствует об успешности тестирования.
, что
свидетельствует об успешности тестирования.
Заметим, что в
приведённом на рис. 3 – 4 примере при коэффициентах отражения от приёмников ![]() структурная
составляющая ЭПР равна
структурная
составляющая ЭПР равна ![]() , а три антенных вместе
, а три антенных вместе ![]() .
.
Выводы
1. Построенная с использованием аппарата матриц рассеяния модель плоской решётки вибраторов над идеально проводящим экраном для фазовой моноимпульсной системы позволяет рассчитывать ДН структурной и антенной составляющих поля рассеяния с учётом схемы возбуждения элементов решётки, а также соответствующие значения дифференциальной ЭПР.
2. Каждая из ДН трёх нормированных антенных составляющих поля рассеяния, имеет точно такую же форму, как соответствующая ДН на передачу. Её уровень зависит от согласования фидера с АР и приёмником, а также от уровня соответствующей ДН в направлении падающей волны.
3. Форма структурной компоненты дифференциальной ЭПР решётки для фазовой моноимпульсной системы в случае согласованных и развязанных входов формирующих многополюсников и суммарно-разностного преобразователя не зависит от АФР, в то время как абсолютное значение ЭПР зависит от АФР. Снижение уровня боковых лепестков суммарной и разностных ДН в направлении падающей волны, уменьшающее величины антенных составляющих ЭПР, приводит к росту структурной компоненты ЭПР.
1. Бененсон Л.С., Фельд Я.Н. Рассеяние электромагнитных волн антеннами (обзор)// Радиотехника и электроника, 1988, т. 33, №2, с. 225 – 245.
2. Сазонов Д.М. Основы матричной теории антенных решёток // Сборник научно-методических статей по прикладной электродинамике. – М.: Высшая школа, 1983, с. 111-162.
3. Пономарёв Л.И., Попов В.В. Рассеивающие свойства антенн и фазированных антенных решёток: Монография. -М.: Изд-во РУДН, 2003,–144 с.
4. Finite Antenna Arrays and FSS / Munk Ben A. - IEEE Press, Wiley – Intersciense, 2003, 357 pp.
5. Modern Antenna Handbook / Balanis Konstantin A. – IEEE Press, Wiley – Intersciense, 2008, 1700 pp.
6. Хансен Р.С. Соотношения между антеннами как рассеивателями и как излучателями // ТИИЭР, 1989, т. 77, №5, с. 30 – 34.
7. Мануилов Б.Д., Кузнецов А.А. Характеристики рассеяния плоских вибраторных решёток при формировании «многолучевых» диаграмм направленности // Антенны, 2012, №1, с. 34 – 42.