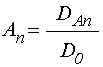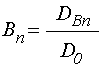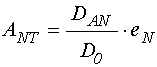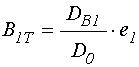УДК 537.874; 537.624
ПРОСТРАНСТВЕННОЕ РАСПРЕДЕЛЕНИЕ АМПЛИТУД ВНЕШНИХ И ВНУТРЕННИХ ВОЛН В ОГРАНИЧЕННОЙ МНОГОСЛОЙНОЙ СТРУКТУРЕ С ПЕРИОДИЧЕСКОЙ НЕОДНОРОДНОСТЬЮ
ЧАСТЬ 1. ОДНОМЕРНАЯ ВОЛНА
И. В. Антонец1, В. Г. Шавров2, В. И. Щеглов2
1 Сыктывкарский государственный университет, Сыктывкар, Россия
2 Институт радиотехники и электроники РАН, Москва, Россия
Статья получена 20 января 2015 г.
Аннотация. Методом пошагового алгоритма рассмотрено распространение волн прямого и обратного направлений в структуре ограниченной длины с периодической неоднородностью меандрового вида. Рассмотрены особенности распространения волн, связанные с периодичностью структуры, выявлен эффект «вторичной модуляции», интерпретированный на основе многорезонаторных свойств структуры. Исследованы амплитуды волн прямого и обратного направлений при изменении координаты или номера слоя структуры, а также среднего волнового числа. Рассмотрена неоднородность пилообразного вида, в том числе влияние формы зубьев пилы на условия распространения волн. Рассмотрено распределение амплитуд в случае большого изменения соотношения между волновыми числами сред, составляющих структуру. Исследована пространственная модуляция амплитуды, в характере которой выявлены пять основных режимов. Для объяснения особенностей пространственной модуляции предложена аналогия с цепочкой последовательно соединенных связанных резонаторов.
Ключевые слова: распространение волн, периодическая структура, пространственная модуляция.
Abstract. By successive steps algorithm method the waves of forward and backward directions propagation in limited length structure with periodical nonuniformity of meander type is investigated. The properties of wave propagation connected with periodicity of structure are explored. It is found the “secondary modulation” effect explained by the multi-resonator properties of structure. It is investigated the forward and backward direction wave amplitudes by the changing of the coordinate or structure slide number and so the average wave number. It is investigated the nonuniformity having similar to saw form and the influence of saw tooth forms on wave propagation conditions. It is investigated the amplitudes distribution in the case of large correlation changing between wave numbers of included in structure media wave numbers. It is investigated the spatial modulation of amplitude. In its character it is found five main regimes. For the explanation of spatial modulation peculiarities it is proposed the analogy with the chain of successive connected related resonators.
Key words: wave propagation, periodical structure, spatial modulation.
Введение
Распространение волн различной природы через слоистые и неоднородные среды издавна привлекает внимание исследователей [1-6]. Особое место здесь занимают задачи, где неоднородность имеет периодический характер [7], возникающие во множестве в электро и радиотехнике, в теории связи, колебаний, теории распространения упругих, электромагнитных или электронных волн в кристаллах, в том числе в магнитных средах [8-14]. Характерным свойством всех периодических сред является наличие чередующихся по частоте полос пропускания и непропускания [7].
Для решения подобных задач традиционно используются методы, основанные на решении уравнений Хилла, Матье или Кронига-Пенни [7,15-17], весьма удачно приспособленные к периодическому характеру среды. Однако в случае хотя бы небольшого нарушения периодичности, например при возникновении какого-нибудь промежуточного барьера, приходится использовать уже классические методы решения задач для сред с произвольными неоднородностями. Наиболее последовательным здесь является прямой метод, состоящий в решении волновых уравнений в каждом слое с последующим их сшиванием на границах [3,4,18,19], однако свойственные этому методу громоздкие определители высоких порядков делают его непригодным уже при количестве сред более пяти. Методы последовательных вычислений – матрицы [18,20] и импеданса [1,2,21], хотя и являются менее громоздкими, однако пригодны для рассмотрения за один проход волн только одного направления без учета встречных волн.
В работах [22-27] предложен универсальный «метод пошагового алгоритма», позволяющий путем крайне простых «пошаговых» алгебраических преобразований получать аналитические выражения для амплитуд как внешних, так и внутренних волн в многослойной структуре со значительным числом слоев. Машинная реализация предложенного алгоритма также крайне проста и содержит всего два цикла, соответствующих прохождению слоев структуры в прямом и обратном направлениях.
В работах [28-32] предложен весьма удобный «метод исключения», позволяющий путем исключения промежуточных вычислений находить амплитуды отраженной и проходящей волн относительно всей структуры в целом. Универсальность метода исключения позволила применить его для рассмотрения периодических структур [31], являющихся частным случаем структур с барьерными неоднородностями. Выгодное преимущество предложенного метода по сравнению с классическими состоит в возможности исследования периодических структур не только с бесконечно большим числом слоев, но и с весьма малым, начиная с одного-двух барьеров, вплоть до бесконечного их числа.
Однако нахождение амплитуд волн в промежуточных слоях структуры методу исключения недоступно.
Настоящая работа посвящена дальнейшему развитию исследований периодических структур с ограниченным числом слоев. В работе [34] выполнено частичное исследование подобных структур при малом изменении волновых чисел в соседствующих слоях. Настоящая работа является продолжением и дальнейшим развитием результатов, полученных в [34], в том числе в случае произвольного соотношения волновых чисел. В дополнение к работе [31], исследование проведено методом алгоритма, что позволяет определить амплитуды волн во всех слоях структуры.
Работа состоит из двух частей. В настоящей части рассмотрение проведено на основе одномерной волны. В следующей части будет произведено обобщение полученных результатов на случай электромагнитных волн.
1. Геометрия задачи
Рассмотрим распространение волны через ограниченную многослойную неоднородную структуру, вид и характер неоднородности в которой по длине структуры периодически повторяется. Предположим, что структура содержит неоднородность в виде одинаковых прямоугольных барьеров, с одинаковыми промежутками между ними. Такую структуру будем называть «меандровой». В случае равенства длины барьеров длине промежутков меандровую структуру будем называть «симметричной». В случае различия упомянутых длин – «несимметричной». Дальнейшее рассмотрение посвящено в первую очередь симметричной меандровой структуре, общая схема которой иллюстрируется рис.1.
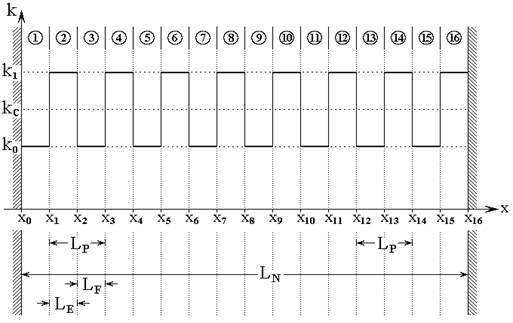
Рис.1. Общая схема ограниченной многослойной структуры с периодической неоднородностью симметричного меандрового вида.
Цифры в кругах – номера слоев (сред).
Число слоев может быть
произвольным, главным требованием является лишь периодическое чередование их
параметров (показан частный случай 16 слоев). Структура содержит два вида сред,
в одном из которых волновое число равно ![]() , а в
другом
, а в
другом ![]() , причем
, причем ![]() . Среднее
значение волнового числа равно:
. Среднее
значение волнового числа равно:
причем добавка к нему ![]() , такова, что:
, такова, что:
Полная длина структуры
равна ![]() . Структура представляет собой совокупность
одинаковых барьеров длиной
. Структура представляет собой совокупность
одинаковых барьеров длиной ![]() , разделенных
промежутками длиной
, разделенных
промежутками длиной ![]() . Период неоднородности
структуры равен:
. Период неоднородности
структуры равен: ![]() .
.
Будем полагать, что отражение волн при
координатах ![]() и
и ![]() отсутствует,
причем в среде №1 распространяется в положительном направлении волна с
амплитудой
отсутствует,
причем в среде №1 распространяется в положительном направлении волна с
амплитудой ![]() , а в среде №16 – в отрицательном
направлении волна с амплитудой
, а в среде №16 – в отрицательном
направлении волна с амплитудой ![]() . Для упрощения записи
экспонент введем обозначения:
. Для упрощения записи
экспонент введем обозначения:
При этом ![]() , где
, где ![]() – начальная фаза, обычно равная нулю.
– начальная фаза, обычно равная нулю.
2. Схема расчета методом пошагового алгоритма
Для расчета амплитуд в слоях такой многослойной структуры будем пользоваться методом пошагового алгоритма [22-27], позволяющим получить значения амплитуд во всех слоях. Приведем сначала общую схему метода алгоритма, после чего дадим ее аналитическую реализацию.
3. Общая схема алгоритма
Рассмотрим алгоритм
получения детерминантов, определяющих амплитуды волн, для произвольного числа ![]() слоев. Алгоритм содержит два этапа,
состоящих в последовательном прохождении по слоям структуры от одного конца структуры
к другому и обратно.
слоев. Алгоритм содержит два этапа,
состоящих в последовательном прохождении по слоям структуры от одного конца структуры
к другому и обратно.
На первом этапе сначала с помощью простых правил задаются вспомогательные величины, определяемые параметрами первого слоя. Эти величины считаются величинами первого слоя. Из них на основе параметров первого и второго слоев формируются новые величины, принадлежащие второму слою. Затем таким же образом из величин второго слоя формируются величины третьего слоя и так далее до тех пор, пока все слои структуры не будут исчерпаны. Формирование последующих величин из предыдущих происходит с помощью формальной процедуры, состоящей в увеличении порядковых индексов всех предыдущих величин на единицу.
При исчерпании всех слоев структуры первый этап заканчивается и происходит переход ко второму. Второй этап начинается с формирования вспомогательных величин, определяемых параметрами последнего слоя структуры. Далее из этих величин с использованием параметров последнего и предпоследнего слоев формируются подобные величины для предпоследнего слоя и так далее, подобно первому этапу, но в обратном порядке. Процедура формирования последующих величин из предыдущих состоит в уменьшении порядковых индексов всех предыдущих величин на единицу.
Таким образом, на первом этапе происходит проход от начала структуры к ее концу, а на втором – обратный ход от конца структуры к ее началу.
Из всех величин, получаемых на обоих этапах, с помощью простых правил суммирования формируются детерминанты, определяющие амплитуды волн внутри слоев.
4. Аналитическая реализация алгоритма
Этап №1.
Сначала введем вспомогательное обозначение:
а также положим начальную тройку основных обозначений:
С использованием (5)-(7) формируем новую тройку выражений:
Далее, увеличивая порядковые номера
индексов на единицу, получаем следующую тройку подобных выражений и так далее,
вплоть до ![]() ,
, ![]() ,
, ![]() . Общие формулы для получения последующих
выражений из предыдущих при произвольном номере
. Общие формулы для получения последующих
выражений из предыдущих при произвольном номере ![]() имеют
вид:
имеют
вид:
Процесс заканчивается при достижении ![]() значения
значения ![]() . При
этом получаем:
. При
этом получаем:
Полученные выражения
используются далее для формирования компонент детерминантов ![]() , соответствующих волнам,
распространяющимся в отрицательном направлении оси
, соответствующих волнам,
распространяющимся в отрицательном направлении оси ![]() (будем
называть это направление обратным).
(будем
называть это направление обратным).
Найдем теперь выражения,
позволяющие формировать компоненты детерминантов ![]() ,
соответствующих волнам, распространяющимся в положительном направлении оси
,
соответствующих волнам, распространяющимся в положительном направлении оси ![]() (которое будем далее называть прямым).
(которое будем далее называть прямым).
Этап №2.
Введем еще одно вспомогательное обозначение:
а также положим другую начальную тройку основных обозначений, индексы которых зададим равными полному количеству слоев:
С использованием (18)-(20) формируем тройку выражений:
Далее, уменьшая порядковые номера
индексов на единицу, получаем следующую тройку подобных выражений и так далее,
вплоть до ![]() ,
, ![]() ,
, ![]() . Общие формулы для получения последующих
выражений из предыдущих при произвольном номере
. Общие формулы для получения последующих
выражений из предыдущих при произвольном номере ![]() имеют
вид:
имеют
вид:
Процесс заканчивается при достижении ![]() значения
значения ![]() . При
этом получаем:
. При
этом получаем:
При этом детерминанты ![]() ,
, ![]() и
и ![]() выражаются через (4)-(29) следующим образом:
выражаются через (4)-(29) следующим образом:
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Здесь индексы детерминантов
соответствуют номерам слоев, а выражения (30) и (37), определяющие ![]() , имея различный вид записи, тождественно
равны.
, имея различный вид записи, тождественно
равны.
Найденные детерминанты (30)-(37)
позволяют определить амплитуды всех волн через ![]() и
и ![]() с помощью формул, задающих амплитуды волн
в точках их исхода:
с помощью формул, задающих амплитуды волн
в точках их исхода:
При этом амплитуда волны, выходящей
из структуры в положительном направлении оси ![]() , в
точке
, в
точке ![]() равна:
равна:
а амплитуда волны, выходящей в
отрицательном направлении оси ![]() , в точке
, в точке ![]() равна:
равна:
Описанный здесь метод был применен для численного расчета амплитуд волн прямого и обратного направлений в структуре, схема которой показана на рис.1. Перейдем к описанию результатов расчетов.
5. Амплитуды волн в крайних слоях структуры
Рассмотрим сначала амплитуды
волн в крайних слоях структуры при изменении волнового числа. Пусть структура
содержит 16 слоев. Полная длина структуры ![]() ,
толщина одного слоя
,
толщина одного слоя ![]() , период неоднородности
, период неоднородности ![]() . На структуру падает одна волна прямого
направления с амплитудой
. На структуру падает одна волна прямого
направления с амплитудой ![]() (при этом
(при этом ![]() ). Рассмотрим изменение среднего волнового
числа
). Рассмотрим изменение среднего волнового
числа ![]() в интервале от
в интервале от ![]() до
до
![]() , причем добавка к нему во всем интервале
его изменения остается постоянной:
, причем добавка к нему во всем интервале
его изменения остается постоянной: ![]() .
.
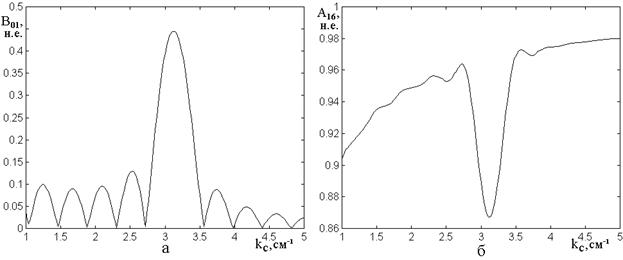
На рис.2 показаны зависимости амплитуд волн обратного (а) и прямого (б) направлений в крайних слоях структуры от среднего волнового числа.
Рис.2. Зависимости амплитуд волн в крайних слоях структуры от среднего волнового числа.
а – волна обратного направления (отраженная) в слое №1.
б – волна прямого направления (проходящая) в слое №16.
Из рисунка видно, что
амплитуды волн как прямого, так и обратного направлений распространения имеют ярко
выраженные особенности вблизи ![]() . При этом амплитуда
волны обратного направления в среде №1 –
. При этом амплитуда
волны обратного направления в среде №1 – ![]() (а)
имеет максимум, что соответствует максимуму отражения падающей волны от
структуры в целом, а амплитуда волны обратного направления в среде №16 –
(а)
имеет максимум, что соответствует максимуму отражения падающей волны от
структуры в целом, а амплитуда волны обратного направления в среде №16 – ![]() (б) имеет минимум, что соответствует минимуму
прохождения падающей волны через структуру в целом.
(б) имеет минимум, что соответствует минимуму
прохождения падающей волны через структуру в целом.
Волновое
число ![]() соответствует длине волны
соответствует длине волны ![]() , что вдвое превышает период изменения
параметров (волнового числа) структуры. То есть на величине периода
укладывается одна половина длины волны. Такое соотношение соответствует хорошо
известному условию прохождения волны через периодическую структуру, говорящему
о наличии полос непропускания при равенстве между периодом структуры и целым
числом распространяющихся в структуре полуволн [7]. Осцилляции по обе стороны
от главного максимума, особенно ярко выраженные для амплитуды отраженной волны
, что вдвое превышает период изменения
параметров (волнового числа) структуры. То есть на величине периода
укладывается одна половина длины волны. Такое соотношение соответствует хорошо
известному условию прохождения волны через периодическую структуру, говорящему
о наличии полос непропускания при равенстве между периодом структуры и целым
числом распространяющихся в структуре полуволн [7]. Осцилляции по обе стороны
от главного максимума, особенно ярко выраженные для амплитуды отраженной волны ![]() , обусловлены интерференционными явлениями
за счет конечности общего числа барьеров структуры. Дополнительный расчет
показывает, что при увеличении количества барьеров амплитуды осцилляций
уменьшаются, причем главный максимум сужается.
, обусловлены интерференционными явлениями
за счет конечности общего числа барьеров структуры. Дополнительный расчет
показывает, что при увеличении количества барьеров амплитуды осцилляций
уменьшаются, причем главный максимум сужается.
6. Амплитуды волн внутри полос непропускания
В общем случае число полос непропускания, чередующихся с полосами пропускания, может быть неопределенно велико. Поэтому представляет интерес оценить амплитуды волн внутри этих полос, что и сделано далее.
Исследование зависимости
амплитуды отраженных и проходящих волн от количества полуволн, укладывающихся
на длине периода структуры, показало, что амплитуда отраженной волны ![]() испытывает осцилляции, максимумы которых
соответствуют нечетному числу полуволн, а минимумы – четному. Однако при
увеличении количества полуволн на периоде структуры различие между максимумами
и минимумами осцилляций убывает.
испытывает осцилляции, максимумы которых
соответствуют нечетному числу полуволн, а минимумы – четному. Однако при
увеличении количества полуволн на периоде структуры различие между максимумами
и минимумами осцилляций убывает.
Дополнительный расчет
показывает, что при дальнейшем увеличении количества полуволн убывание между
максимумами и минимумами сменяется нарастанием и затем снова убыванием. Так при
![]() и
и ![]() величина
величина
![]() составляет соответственно
составляет соответственно ![]() и
и ![]() , а при
, а при
![]() и
и ![]() –
– ![]() и
и ![]() . Более
подробное исследование выявляет четкую периодичность таких изменений с периодом
по волновому числу около
. Более
подробное исследование выявляет четкую периодичность таких изменений с периодом
по волновому числу около ![]() , причем величина
периода с увеличением различия между волновыми числами в слоях структуры
, причем величина
периода с увеличением различия между волновыми числами в слоях структуры ![]() и
и ![]() уменьшается.
Амплитуда проходящей волны
уменьшается.
Амплитуда проходящей волны ![]() ведет себя подобным же
образом, однако в противофазе с амплитудой
ведет себя подобным же
образом, однако в противофазе с амплитудой ![]() , что
обусловлено энергетическим балансом системы в целом.
, что
обусловлено энергетическим балансом системы в целом.
Подобную осцилляцию амплитуд отраженной и проходящей волн при изменении среднего волнового числа можно назвать «вторичной модуляцией», проявление которой в подобных структурах впервые было отмечено в работе [31]. Причина вторичной модуляции, по-видимому, связана с тем, что в структуре барьеры и промежутки между ними представляют собой ограниченные с двух сторон участки однородной среды, то есть обладают определенными резонансными свойствами. Поскольку имеются только два вида таких участков, то и резонансных частот получается всего две. Таким образом, волна распространяется через цепочку распределенных резонаторов, частоты которых чередуются. Такое распространение приводит к биению между этими частотами, в результате чего появляется разностная частота с периодом значительно большим, чем исходные. Этот период и проявляет себя в периодическом изменении амплитуды пиков отражения. При увеличении разности между частотами составляющих структуру резонаторов (то есть между значениями скоростей в них) частота биений увеличивается, в результате чего период вторичной модуляции уменьшается, как это и отмечено выше.
7. Амплитуды волн в различных слоях структуры
Рассмотрим теперь, что происходит с волнами прямого и обратного направлений при изменении координаты или номера слоя структуры, а также при изменении среднего волнового числа.
8. Изменение номера слоя структуры
По мере распространения в прямом или обратном направлении волна последовательно проходит от одного слоя структуры к другому, причем амплитуды волн в различных слоях получаются различными.
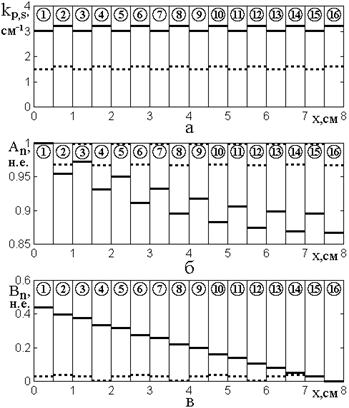
Рис.3. Зависимости волновых чисел (а) и амплитуд волн прямого (б) и обратного (в) направлений от координаты в различных слоях структуры.
Утолщенные сплошные горизонтальные
линии построены при среднем волновом числе ![]() (
(![]() ,
, ![]() ); утолщенные
пунктирные линии – при
); утолщенные
пунктирные линии – при ![]() (
(![]() ,
, ![]() ).
).
Такое их поведение
иллюстрируется рис.3, где показаны зависимости волновых чисел (а) и амплитуд
волн прямого (б) и обратного (в) направлений от координаты в различных слоях
структуры при различных значениях среднего волнового числа. Сплошные
горизонтальные линии соответствуют волновому числу в середине первой полосы
непропускания (![]() ), пунктирные горизонтальные
линии – волновому числу вдали от такой полосы (
), пунктирные горизонтальные
линии – волновому числу вдали от такой полосы (![]() ).
).
Из рисунка видно, что в
полосе непропускания амплитуды волн прямого направления (б) по мере увеличения
номера среды монотонно падают от ![]() в среде №1 до
в среде №1 до ![]() в среде №16, тогда как амплитуды тех же
волн вне полосы непропускания, перемежаясь, осциллируют между
в среде №16, тогда как амплитуды тех же
волн вне полосы непропускания, перемежаясь, осциллируют между ![]() и
и ![]() с периодом,
равным периоду структуры. Амплитуды волн обратного направления (в) в тех же
условиях в полосе непропускания монотонно спадают от
с периодом,
равным периоду структуры. Амплитуды волн обратного направления (в) в тех же
условиях в полосе непропускания монотонно спадают от ![]() в
среде №1 до
в
среде №1 до ![]() в среде №16, тогда как вне полосы
непропускания осциллируют между
в среде №16, тогда как вне полосы
непропускания осциллируют между ![]() и
и ![]() с периодом близким к удвоенному периоду
структуры.
с периодом близким к удвоенному периоду
структуры.
Такое поведение амплитуд волн обоих направлений соответствует постепенному просачиванию волны через структуру с убыванием энергии волны в полосе непропускания и сохранением ее энергии вне такой полосы.
Поведение амплитуд волн в других различных полосах непропускания и вне таких полос соответствует описанному при рассмотрении рис.3, с тем отличием, что при увеличении номера полосы проявляется эффект вторичной модуляции, рассмотренный в предыдущем разделе. При этом монотонный характер спада и нарастания волн в полосе непропускания сохраняется, однако амплитуды волн обоих направлений в среде №1 периодически осциллируют с периодом, равным периоду вторичной модуляции.
Период осцилляций
зависимости ![]() (рис.4в, пунктирные линии), будучи первоначально
близким к удвоенному периоду структуры, постепенно увеличивается, достигая,
например, в десятой полосе непропускания величины порядка пяти-шести периодов
структуры.
(рис.4в, пунктирные линии), будучи первоначально
близким к удвоенному периоду структуры, постепенно увеличивается, достигая,
например, в десятой полосе непропускания величины порядка пяти-шести периодов
структуры.
9. Изменение среднего волнового числа
Рассмотрим теперь
амплитуды волн в различных слоях структуры. Поведение амплитуд при изменении
волнового числа для волн обратного (а) и прямого (б) направлений иллюстрируется
рис.4. Все параметры структуры – те же, что использовались при построении
рис.1, добавка к волновому числу также постоянна и равна ![]() .
.
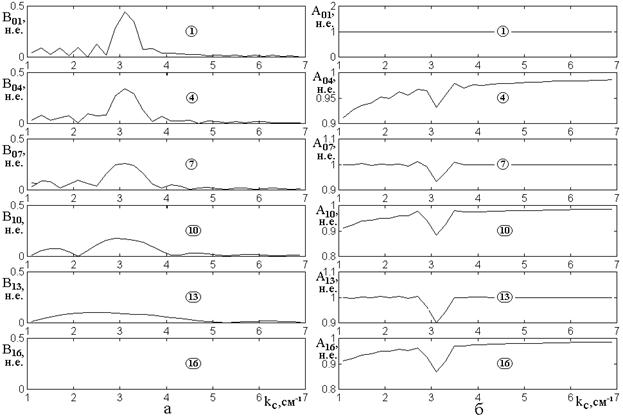
Рис.4. Зависимости амплитуд волн обратного (а) и прямого (б) направлений в различных слоях структуры от среднего волнового числа.
Цифры в кругах – номера слоев.
Из рисунков видно, что
зависимости для волн обоих направлений имеют экстремумы вблизи ![]() , что соответствует первой полосе непропускания.
В окрестности волнового числа
, что соответствует первой полосе непропускания.
В окрестности волнового числа ![]() , соответствующего
второй полосе непропускания, видимые экстремумы отсутствуют благодаря явлению
вторичной модуляции, рассмотренному в предыдущем разделе.
, соответствующего
второй полосе непропускания, видимые экстремумы отсутствуют благодаря явлению
вторичной модуляции, рассмотренному в предыдущем разделе.
Интенсивный максимум
зависимости ![]() от
от ![]() по
мере увеличения номера среды, то есть удалении от точки возбуждения, постепенно
расплывается, амплитуда его падает, экстремальный характер рассасывается,
переходя в монотонно спадающий, стремящийся к нулю по мере приближения к
крайнему слою структуры (№16).
по
мере увеличения номера среды, то есть удалении от точки возбуждения, постепенно
расплывается, амплитуда его падает, экстремальный характер рассасывается,
переходя в монотонно спадающий, стремящийся к нулю по мере приближения к
крайнему слою структуры (№16).
Зависимости для волн
обратного направления чередуются: в слоях с четными номерами они имеют
выпуклость вверх и возрастают по мере увеличения ![]() , в
слоях с нечетными номерами – осциллируют с крайне малой амплитудой (менее 10%)
в окрестности единицы.
, в
слоях с нечетными номерами – осциллируют с крайне малой амплитудой (менее 10%)
в окрестности единицы.
Такие два вида поведения обусловлены тем, что в слоях с нечетными номерами волновые числа те же, что в первой среде, а с нечетными – отличные от первых. То есть во всех нечетных средах волны находятся в тех же условиях, что и на входе в структуру, тогда как в нечетных – в условиях отличных. Поэтому, в случае изменения условий параметры волны испытывают как бы скачок, тогда как при сохранении условий такой скачок отсутствует.
Некоторое превышение амплитуд волн над единицей в процессе осцилляций в нечетных средах отражает увеличение амплитуды волны при прохождении из более плотной среды в менее плотную, то есть от слоя с большим волновым числом к слою с меньшим.
10. Неоднородность пилообразного вида
В качестве еще одного примера рассмотрим распространение волны через структуру с периодической неоднородностью пилообразного вида, иллюстрируемое рис.5.
На рис.5а для частного
случая 16 слоев показана схема распределения волновых чисел, меняющихся по
координате от слоя к слою по «пилообразному» закону, при котором каждый зубец
«пилы» представлен в виде четырехступенчатой ломаной линии. Таким образом
структура содержит четыре вида сред с равноотстоящими друг от друга четырьмя
волновыми числами ![]() ,
, ![]() ,
, ![]() ,
, ![]() , где
, где ![]() , причем
, причем ![]() .
Среднее волновое число определяется соотношением:
.
Среднее волновое число определяется соотношением:
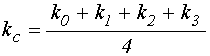 . (41)
. (41)
При этом волновые числа в первых четырех средах равны:
![]() ; (42)
; (42)
![]() ; (43)
; (43)
![]() ; (44)
; (44)
![]() . (45)
. (45)
При номере слоев больше ![]() все параметры сред периодически повторяются.
Полная длина структуры равна
все параметры сред периодически повторяются.
Полная длина структуры равна ![]() . В общем случае такую
периодическую структуру можно рассматривать как совокупность одинаковых «треугольных»
барьеров длиной
. В общем случае такую
периодическую структуру можно рассматривать как совокупность одинаковых «треугольных»
барьеров длиной ![]() , внутри которых волновое число
по координате
, внутри которых волновое число
по координате ![]() возрастает по ступенчато-прямолинейному
закону (42)-(45).
возрастает по ступенчато-прямолинейному
закону (42)-(45).
На рис.5 в пределах ![]() помещается четыре «зубца пилы», то есть
четыре периода
помещается четыре «зубца пилы», то есть
четыре периода ![]() . Дополнительное исследование показывает,
что в такой структуре, аналогично меандровой, имеются полосы непропускания,
соответствующие укладыванию половины длины волны на периоде структуры. При
этом, учитывая, что период структуры равен
. Дополнительное исследование показывает,
что в такой структуре, аналогично меандровой, имеются полосы непропускания,
соответствующие укладыванию половины длины волны на периоде структуры. При
этом, учитывая, что период структуры равен ![]() ,
получаем, что первая полоса непропускания соответствует
,
получаем, что первая полоса непропускания соответствует ![]() (длина
волны
(длина
волны ![]() ). Поэтому на рис.5 представлены два вида
зависимостей, первый – соответствующий первой полосе непропускания при
). Поэтому на рис.5 представлены два вида
зависимостей, первый – соответствующий первой полосе непропускания при ![]() (сплошные горизонтальные линии), второй –
вне такой полосы при
(сплошные горизонтальные линии), второй –
вне такой полосы при ![]() (пунктирные горизонтальные линии).
(пунктирные горизонтальные линии).
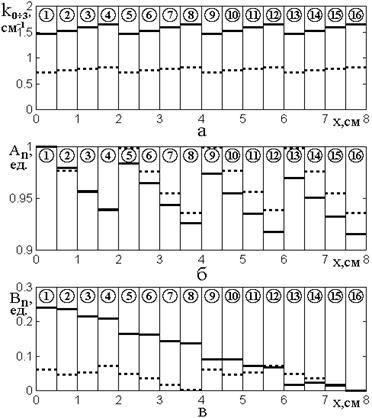
Рис.5. Зависимости волновых чисел (а) и амплитуд волн прямого (б) и обратного (в) направлений от координаты в различных слоях структуры.
Утолщенные
сплошные горизонтальные линии построены при среднем волновом числе ![]() (
(![]() ,
, ![]() ,
, ![]() ,
, ![]() ); утолщенные пунктирные горизонтальные
линии – при
); утолщенные пунктирные горизонтальные
линии – при ![]() (
(![]() ,
, ![]() ,
, ![]() ,
, ![]() ).
).
11. Амплитуды волн в различных слоях структуры
На рис.5, кроме волновых чисел (а), показаны зависимости от координаты для амплитуд волн прямого (б) и обратного (в) направлений в различных слоях структуры.
Из рисунка видно, что в
полосе непропускания амплитуды волн прямого направления (б) по мере увеличения
номера среды на каждом периоде зависимости ![]() монотонно
падают: на первом периоде от
монотонно
падают: на первом периоде от ![]() в среде №1 до
в среде №1 до ![]() в среде №4, после чего на границе между
средами №4 и №5 резко возрастают до
в среде №4, после чего на границе между
средами №4 и №5 резко возрастают до ![]() , на втором периоде
опять падают от
, на втором периоде
опять падают от ![]() в среде №5 до
в среде №5 до ![]() в среде №8, затем на границе сред №8 и №9
возрастают до
в среде №8, затем на границе сред №8 и №9
возрастают до ![]() , после чего снова падают и так
далее. Вне полосы непропускания амплитуды волн прямого направления на каждом
периоде монотонно спадают от
, после чего снова падают и так
далее. Вне полосы непропускания амплитуды волн прямого направления на каждом
периоде монотонно спадают от ![]() в средах №№ 1, 5, 9,
13 до
в средах №№ 1, 5, 9,
13 до ![]() в средах №№ 4, 8, 12, 16. То есть, в
общем, в полосе непропускания амплитуды волн прямого направления имеют
тенденцию к убыванию, тогда как вне полосы непропускания такая тенденция
отсутствует.
в средах №№ 4, 8, 12, 16. То есть, в
общем, в полосе непропускания амплитуды волн прямого направления имеют
тенденцию к убыванию, тогда как вне полосы непропускания такая тенденция
отсутствует.
В
полосе непропускания амплитуды волн обратного направления (в) по мере увеличения
номера среды монотонно спадают от ![]() в среде №1 до
в среде №1 до ![]() в среде №16. Амплитуды волн того же
обратного направления вне полосы непропускания по мере увеличения номера среды
осциллируют с размахом от
в среде №16. Амплитуды волн того же
обратного направления вне полосы непропускания по мере увеличения номера среды
осциллируют с размахом от ![]() в средах №4 и №12 до
в средах №4 и №12 до ![]() в средах №8 и №16, причем период осцилляций
составляет около
в средах №8 и №16, причем период осцилляций
составляет около ![]() . Таким образом, в полосе
непропускания амплитуды волн обратного направления имеют тенденцию к уменьшению,
тогда как вне той же полосы такая тенденция отсутствует.
. Таким образом, в полосе
непропускания амплитуды волн обратного направления имеют тенденцию к уменьшению,
тогда как вне той же полосы такая тенденция отсутствует.
12. Сопоставление со случаем меандровой неоднородности
Таким образом, из сопоставления рис.5 с рис.3 для меандровой неоднородности можно видеть, что в случае пилообразной неоднородности амплитуды волн прямого и обратного направлений, в основном, качественно, ведут себя подобно аналогичным амплитудам волн в случае неоднородности типа меандра.
Явное количественное
различие наблюдается в амплитудах. Так в полосе непропускания для волн прямого
направления в среде №16 амплитуда ![]() в случае меандровой
неоднородности составляет
в случае меандровой
неоднородности составляет ![]() , тогда как в случае
пилообразной –
, тогда как в случае
пилообразной – ![]() . В той же полосе для волн
обратного направления в среде №1 амплитуда
. В той же полосе для волн
обратного направления в среде №1 амплитуда ![]() в
случае меандровой неоднородности составляет
в
случае меандровой неоднородности составляет ![]() , тогда
как в случае пилообразной –
, тогда
как в случае пилообразной – ![]() . Амплитуды осцилляций
вне полосы непропускания для волн обратного направления в случае меандровой
неоднородности составляет
. Амплитуды осцилляций
вне полосы непропускания для волн обратного направления в случае меандровой
неоднородности составляет ![]() , тогда как в случае
пилообразной – всего
, тогда как в случае
пилообразной – всего ![]() .
.
Таким образом, можно
видеть, что при одной и той же величине добавки к среднему волновому числу (![]() ) пилообразная неоднородность на
амплитудах распространяющихся волн сказывается значительно слабее, чем
меандровая (приблизительно в полтора-два раза).
) пилообразная неоднородность на
амплитудах распространяющихся волн сказывается значительно слабее, чем
меандровая (приблизительно в полтора-два раза).
Другим важнейшим
различием можно считать изменение скорости нарастания осцилляций по координате ![]() . Однако такое различие является вполне
ожидаемым и связано с изменением величины периода пилообразной структуры по
отношению к периоду меандровой. Действительно, поскольку период пилообразной
структуры (рис.5) по отношению к меандровой (рис.3) увеличивается в два раза (с
. Однако такое различие является вполне
ожидаемым и связано с изменением величины периода пилообразной структуры по
отношению к периоду меандровой. Действительно, поскольку период пилообразной
структуры (рис.5) по отношению к меандровой (рис.3) увеличивается в два раза (с
![]() до
до ![]() ), то и
скорость изменения амплитуды, например, волны прямого направления (
), то и
скорость изменения амплитуды, например, волны прямого направления (![]() на рис.3б и
на рис.3б и ![]() на
рис.5б) уменьшается, хотя и несколько меньше, чем в два раза (то есть с
на
рис.5б) уменьшается, хотя и несколько меньше, чем в два раза (то есть с ![]() до
до ![]() ).
Скорость спада амплитуды волны обратного направления (от
).
Скорость спада амплитуды волны обратного направления (от ![]() до
до ![]() ) также
уменьшается почти в два раза (с
) также
уменьшается почти в два раза (с ![]() на рис.3в до
на рис.3в до ![]() на рис.5в).
на рис.5в).
Дополнительное исследование показывает, что при уменьшении периода пилообразной неоднородности вплоть до периода меандровой эти численные различия сглаживаются и амплитуды волн обоих направлений при пилообразной неоднородности приближаются к амплитудам таких же волн при неоднородности меандровой. То есть тонкая структура «зубца» пилы проявляется тем слабее, чем ближе его длина приближается к длине барьера меандра. При увеличении периода пилообразной неоднородности вплоть до полной длины структуры в целом (то есть когда из всей пилы остается лишь один зубец), характер распространения волн обоих направлений приближается к таковому для случая линейной неоднородности.
При изменении наклона зубцов пилы с положительного на отрицательное (то есть с наклона вперед к наклону назад) распределение амплитуд в слоях для волн прямого направления практически не меняется (при приведенных выше параметрах – с точностью до четвертого-пятого знака), а для волн обратного направления, хотя и меняется, но крайне мало (не более чем на единицы или доли процента).
13. Пространственная модуляция амплитуды
В предыдущих разделах
было рассмотрено распределение амплитуд для сравнительно малого изменения
волнового числа от слоя к слою. Так для рис.3 среднее волновое число составляет
![]() , а волновые числа в чередующихся слоях
структуры равны
, а волновые числа в чередующихся слоях
структуры равны ![]() и
и ![]() , то
есть соотношение между ними
, то
есть соотношение между ними ![]() составляет всего
составляет всего ![]() , то есть отклонение от среднего значения
не превышает
, то есть отклонение от среднего значения
не превышает ![]() .
.
Рассмотрим теперь, что происходит с амплитудами волн обоих направлений при более сильном изменении соотношения между волновыми числами двух видов сред, составляющих структуру.
Исследование показывает, что при увеличении такого соотношения распределение амплитуд волн в слоях структуры приобретает зависящий от координаты характер, то есть имеет место пространственная модуляция этой амплитуды.
На данном этапе ограничимся рассмотрением периодической структуры в виде симметричного меандра, то есть такой, которая состоит из слоев одинаковой толщины, имеющих чередующиеся волновые свойства, в качестве которых за основу примем волновое число.
14. Основные режимы пространственной модуляции
В поведении
пространственной модуляции в зависимости от соотношения волновых чисел в
соседствующих слоях ![]() можно выделить пять характерных
режимов: синусоидальный, полусинусоидальный, линейный, экспоненциальный и
синусоидальный с верхним пределом, соответствующих различным интервалам значений
такого соотношения.
можно выделить пять характерных
режимов: синусоидальный, полусинусоидальный, линейный, экспоненциальный и
синусоидальный с верхним пределом, соответствующих различным интервалам значений
такого соотношения.
Будем
полагать, что волна падает со стороны начала структуры (![]() ,
,![]() ), и сначала рассмотрим характерные
свойства этих режимов, после чего установим интервалы их существования.
), и сначала рассмотрим характерные
свойства этих режимов, после чего установим интервалы их существования.
Режим №1 – синусоидальные колебания амплитуды.
В этом случае
распределение амплитуды колебаний по координате имеет вид довольно правильной
синусоиды, не имеющей ограничения сверху или снизу по своему значению. Типичная
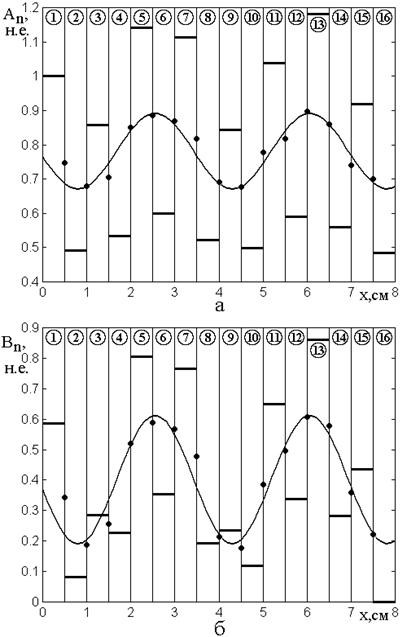
картина распределения амплитуд для такого режима иллюстрируется рис.6, где
показаны зависимости амплитуд волн прямого (а) и обратного (б) направлений от
координаты в различных слоях структуры. Рисунок построен при отклонении
значений волновых чисел в слоях от среднего значения на ![]() .
Укрупненные точки являются результатами машинного эксперимента и построены как
середины перепадов между амплитудами волн в соседствующих слоях. Синусоидальная
кривая на рис.6а построена по эмпирической формуле:
.
Укрупненные точки являются результатами машинного эксперимента и построены как
середины перепадов между амплитудами волн в соседствующих слоях. Синусоидальная
кривая на рис.6а построена по эмпирической формуле:
![]() , (46)
, (46)
подобная кривая на рис.6б построена по формуле:
![]() .
(47)
.
(47)
Из рисунка видно, что в
этом режиме линии, проведенные через экспериментальные точки, близки к
многократно осциллирующим синусоидам, вследствие чего режим назван
«синусоидальным». При этом эмпирические кривые согласуются с точками, в
основном, с точностью не хуже ![]() . Несколько большие
отклонения наблюдаются только на границе между первым и вторым слоями, где для
волн прямого направления отличие составляет
. Несколько большие
отклонения наблюдаются только на границе между первым и вторым слоями, где для
волн прямого направления отличие составляет ![]() , а для
волн обратного –
, а для
волн обратного – ![]() , что, по-видимому, связано с
недостаточным установлением режима распространения волн вблизи точки их
излучения.
, что, по-видимому, связано с
недостаточным установлением режима распространения волн вблизи точки их
излучения.
Рис.6. Зависимости амплитуд волн прямого (а) и обратного (б) направлений от координаты в различных слоях структуры.
Утолщенные горизонтальные линии – амплитуды волн в слоях.
Волновые числа: ![]() ,
, ![]() ,
, ![]() .
.
Как видно из приведенных формул, частоты и фазы обеих кривых совпадают, однако амплитуды и постоянные составляющие значительно различаются. Так амплитуда синусоиды, соответствующей волнам прямого направления, примерно в два раза меньше амплитуды синусоиды волн обратного направления, а соотношение для постоянных составляющих – обратное: постоянная составляющая синусоиды для волн прямого направления примерно в два раза больше подобной составляющей для волн обратного направления.
Такой синусоидальный
характер полученных кривых говорит о том, что для обоих направлений перепады
амплитуд волн в соседних слоях по мере изменения координаты периодически
осциллируют. Период осцилляций амплитуды здесь равен ![]() ,
что соответствует изменению аргумента синуса на
,
что соответствует изменению аргумента синуса на ![]() ,
причем этот период одинаков для волн обоих направлений.
,
причем этот период одинаков для волн обоих направлений.
Режим №2 – полусинусоидальное изменение амплитуды.
В этом случае распределение амплитуды по координате напоминает по форме положительную половину периода синусоиды, вследствие чего режим назван «полусинусоидальным». Типичная картина распределения амплитуд для такого режима иллюстрируется рис.7, где показаны зависимости амплитуд волн прямого (сплошные линии и закрытые точки) и обратного (пунктирные линии и открытые точки) направлений от координаты в различных слоях структуры.
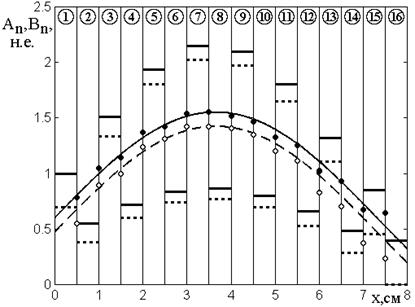
Рис.7. Зависимости амплитуд волн прямого (сплошные линии и закрытые точки) и обратного (пунктирные линии и открытые точки) направлений от координаты в различных слоях структуры.
Кривые построены по формулам (48) и (49).
Волновые числа: ![]() ,
, ![]() ,
, ![]() .
.
Рисунок построен при
отклонении значений волновых чисел в слоях от среднего значения на ![]() . Укрупненные точки являются результатами
машинного эксперимента и построены как середины перепадов между амплитудами
волн в соседствующих слоях. Сплошная кривая построена по эмпирической формуле:
. Укрупненные точки являются результатами
машинного эксперимента и построены как середины перепадов между амплитудами
волн в соседствующих слоях. Сплошная кривая построена по эмпирической формуле:
![]() , (48)
, (48)
пунктирная кривая построена по формуле:
![]() . (49)
. (49)
Из рисунка видно, что как
и при синусоидальном режиме частоты и фазы обеих кривых совпадают, здесь же
совпадают также и амплитуды, а различаются только постоянные составляющие,
причем всего на ![]() от среднего значения (
от среднего значения (![]() ). То есть зависимости амплитуд волн обоих
направлений от координаты, в отличие от синусоидального режима, почти
совпадают. Если принять наблюдаемую половину синусоиды за половину периода осцилляций,
то можно видеть, что здесь он равен
). То есть зависимости амплитуд волн обоих
направлений от координаты, в отличие от синусоидального режима, почти
совпадают. Если принять наблюдаемую половину синусоиды за половину периода осцилляций,
то можно видеть, что здесь он равен ![]() и одинаков для волн
обоих направлений.
и одинаков для волн
обоих направлений.
Режим №3 – линейный спад амплитуды.
В этом режиме амплитуда
по координате спадает линейным образом. Типичная картина распределения амплитуд
для такого режима иллюстрируется рис.8, где показаны зависимости амплитуд волн
прямого (сплошные линии и закрытые точки) и обратного (пунктирные линии и
открытые точки) направлений от координаты в различных слоях структуры. Рисунок
построен при отклонении значений волновых чисел в слоях от среднего значения на
![]() . Укрупненные точки являются результатами
машинного эксперимента и построены как середины перепадов между амплитудами
волн в соседствующих слоях. Сплошная линия построена по эмпирической формуле:
. Укрупненные точки являются результатами
машинного эксперимента и построены как середины перепадов между амплитудами
волн в соседствующих слоях. Сплошная линия построена по эмпирической формуле:
![]() , (50)
, (50)
пунктирная – построена формуле:
![]() . (51)
. (51)
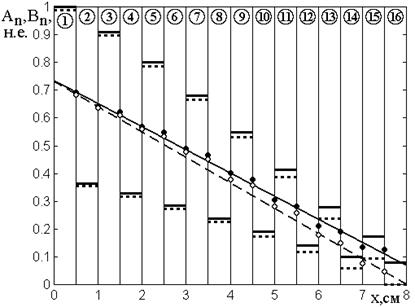
Рис.8. Зависимости амплитуд волн прямого (сплошные линии и закрытые точки) и обратного (пунктирные линии и открытые точки) направлений от координаты в различных слоях структуры.
Прямые построены по формулам (50) и (51).
Волновые числа: ![]() ,
, ![]() ,
, ![]() .
.
Из рисунка видно, что в этом режиме линии, проведенные через экспериментальные точки, являются прямыми, вследствие чего режим назван «линейным».
В отличие от
синусоидального и полусинусоидального режимов здесь какая либо периодичность
зависимостей полностью отсутствует, постоянные составляющие для волн обоих
направлений совпадают, а угловые коэффициенты прямых слегка различаются, хотя и
незначительно – всего на ![]() от среднего значения (
от среднего значения (![]() ). Зависимости амплитуд волн того и
другого направлений от координаты при малых номерах слоев (до 10) практически
совпадают (с точностью до
). Зависимости амплитуд волн того и
другого направлений от координаты при малых номерах слоев (до 10) практически
совпадают (с точностью до ![]() ) и только при слоях с
номерами 14 и 15, то есть вблизи конца структуры, достигают
) и только при слоях с
номерами 14 и 15, то есть вблизи конца структуры, достигают ![]() .
.
Режим №4 – экспоненциальный спад амплитуды.
В этом режиме амплитуда
колебаний по координате спадает сначала резко, а потом более плавно. С
достаточной точностью такой спад можно приблизить экспонентой, благодаря чему
приближению этот режим назван «экспоненциальным». Типичная картина
распределения амплитуд для такого режима иллюстрируется рис.9, где показаны
зависимости амплитуд волн прямого и обратного направлений от координаты в
различных слоях структуры. Амплитуды волн прямого и обратного направлений в
каждом слое попарно совпадают друг с другом с точностью в доли процента,
поэтому приведенные на рисунке амплитуды, точки и приближающая кривая
соответствуют волнам как того, так и другого направлений в равной степени.
Рисунок построен при отклонении значений волновых чисел в слоях от среднего
значения на ![]() . Спадающая кривая построена по
эмпирической формуле:
. Спадающая кривая построена по
эмпирической формуле:
![]() . (52)
. (52)
На врезке – те же
зависимости в логарифмическом масштабе по вертикальной оси. Сплошные
горизонтальные линии соответствуют ![]() , пунктирные –
, пунктирные – ![]() . Видно, что здесь, начиная с
. Видно, что здесь, начиная с ![]() , они несколько различаются тем сильнее,
чем больше
, они несколько различаются тем сильнее,
чем больше ![]() . Такое различие обусловлено растягивающим
действием логарифмического масштаба при малых амплитудах.
. Такое различие обусловлено растягивающим
действием логарифмического масштаба при малых амплитудах.
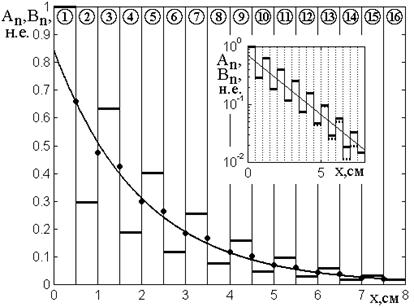
Рис.9. Зависимости амплитуд волн прямого и обратного
направлений (совпадают) от координаты в различных слоях структуры.
Спадающая кривая построена по формуле (52).
Волновые числа: ![]() ,
, ![]() ,
, ![]() .
.
Из рисунка видно, что в логарифмическом масштабе (врезка) зависимость амплитуд от координаты с высокой точностью (доли процента) представляет собой прямую линию, что говорит о хорошем приближении экспериментальных данных спадающей экспонентой, что оправдывает название режима. В этом режиме зависимости амплитуд волн обоих направлений от координаты практически полностью совпадают.
Дополнительное
исследование показывает, что спад экспоненты при увеличении отношения волновых
чисел от ![]() до
до ![]() увеличивается,
причем коэффициент при переменной в ее показателе меняется в пределах от
увеличивается,
причем коэффициент при переменной в ее показателе меняется в пределах от ![]() до
до ![]() . В
остальном характер режима полностью сохраняется.
. В
остальном характер режима полностью сохраняется.
Режим №5 – синусоидальные колебания амплитуды с верхним пределом.
В этом случае
распределение амплитуды колебаний по координате, как и при режиме №1, имеет вид
довольно правильной синусоиды, однако здесь все амплитуды ограничены сверху
определенным значением, единым для всех слоев. Благодаря такому ограничению в названии
режима присутствует формулировка «с верхним пределом». Типичная картина
распределения амплитуд для такого режима иллюстрируется рис.10, где показаны
зависимости амплитуд волн прямого (сплошные линии и точки) и обратного
(пунктирные линии и открытые точки) направлений от координаты в различных слоях
структуры. Рисунок построен при отклонении значений волновых чисел в слоях от
среднего значения на ![]() . Укрупненные точки являются
результатами машинного эксперимента и построены как середины перепадов между
амплитудами волн в соседствующих слоях. Сплошная синусоидальная кривая
построена по формуле:
. Укрупненные точки являются
результатами машинного эксперимента и построены как середины перепадов между
амплитудами волн в соседствующих слоях. Сплошная синусоидальная кривая
построена по формуле:
![]() ,
(53)
,
(53)
пунктирная – по формуле:
![]() .
(54)
.
(54)
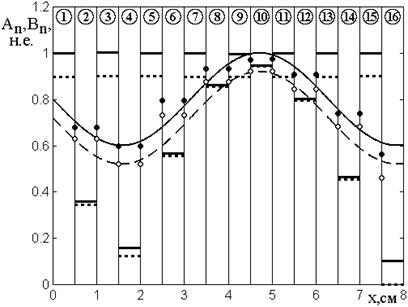
Рис.10. Зависимости амплитуд волн прямого (сплошные линии и точки) и обратного (пунктирные линии и открытые точки) направлений от координаты в различных слоях структуры.
Сплошная кривая построена по формуле (53), пунктирная – по формуле (54).
Волновые числа: ![]() ,
, ![]() ,
, ![]() .
.
Из рисунка видно, что в
этом режиме синусоидальные кривые ведут себя подобно таковым при режиме №1,
причем здесь они совпадают не только по фазе, но и по амплитуде. Период
осцилляций составляет ![]() , что соответствует изменению
аргумента синуса на
, что соответствует изменению
аргумента синуса на ![]() . Однако соответствие между упомянутыми
кривыми и экспериментальными точками здесь несколько хуже, чем при режиме №1 и
в ряде слоев отклонение достигает
. Однако соответствие между упомянутыми
кривыми и экспериментальными точками здесь несколько хуже, чем при режиме №1 и
в ряде слоев отклонение достигает ![]() .
.
Амплитуды колебаний в
слоях с четными и нечетными номерами ведут себя существенно различным образом.
Так амплитуды для нечетных слоев все ограничены сверху одним и тем же
значением, для волн прямого направления близким к единице, а для волн обратного
направления – близким к величине ![]() Амплитуды волн в
четных слоях везде меньше этих значений. Исключение составляет только амплитуда
волны обратного направления в слое №10, где она равна
Амплитуды волн в
четных слоях везде меньше этих значений. Исключение составляет только амплитуда
волны обратного направления в слое №10, где она равна ![]() ,
что впрочем, отличается от основного значения всего на
,
что впрочем, отличается от основного значения всего на ![]() ,
то есть весьма незначительно.
,
то есть весьма незначительно.
Причина отмеченного несколько неполного соответствия синусоидальных кривых экспериментальным точкам состоит в равенстве перепадов между амплитудами соседствующих слоев для слоев с четными номерами.
15. Интервалы существования различных режимов
При увеличении
соотношения между волновыми числами составляющих структуру сред в пределах ![]() описанные выше режимы №1-№4 по очереди
сменяют друг друга следующим образом: при
описанные выше режимы №1-№4 по очереди
сменяют друг друга следующим образом: при ![]() имеет
место синусоидальный режим №1; при
имеет
место синусоидальный режим №1; при ![]() – полусинусоидальный
№2; при
– полусинусоидальный
№2; при ![]() – линейный №3; при
– линейный №3; при ![]() – экспоненциальный №4.
– экспоненциальный №4.
Далее наблюдаются широкие интервалы господства экспоненциального режима №4, перемежаемые относительно узкими «островками» синусоидального режима №5, где амплитуды ограничены верхним пределом. Так
при ![]() в
интервале
в
интервале ![]() наблюдается режим №4,
наблюдается режим №4,
при ![]() в
интервале
в
интервале ![]() – режим №5,
– режим №5,
при ![]() в
интервале
в
интервале ![]() – режим №4,
– режим №4,
при ![]() в
интервале
в
интервале ![]() – режим №5,
– режим №5,
при ![]() в интервале
в интервале
![]() – режим №4 и т. д. Как видим, интервалы
существования режима №5 заметно короче интервалов режима №4, причем с увеличением
отношения
– режим №4 и т. д. Как видим, интервалы
существования режима №5 заметно короче интервалов режима №4, причем с увеличением
отношения ![]() интервалы режима №5 сужаются.
интервалы режима №5 сужаются.
Границы между всеми режимами являются плавными, какие-либо скачки отсутствуют, однако интервалы изменения режимов, как правило, значительно короче интервалов, где режимы существуют в устойчивом виде.
Из
сравнения величин интервалов существования режимов по величине ![]() при
при ![]() можно
видеть, что наиболее протяженными, то есть основными режимами являются
синусоидальный и экспоненциальный, занимающие интервалы
можно
видеть, что наиболее протяженными, то есть основными режимами являются
синусоидальный и экспоненциальный, занимающие интервалы ![]() и
и
![]() относительных единиц соответственно,
тогда как на долю полусинусоидального и линейного режимов приходятся интервалы
всего по
относительных единиц соответственно,
тогда как на долю полусинусоидального и линейного режимов приходятся интервалы
всего по ![]() относительных единиц. То есть основными
режимами являются синусоидальный и экспоненциальный, а режимы полусинусоидальный
и линейный – переходными.
относительных единиц. То есть основными
режимами являются синусоидальный и экспоненциальный, а режимы полусинусоидальный
и линейный – переходными.
16. Динамика переходов между режимами
Рассмотрим теперь, как
именно происходят переходы между режимами по мере увеличения отношения волновых
чисел. Начнем с синусоидального режима, как соответствующего наименьшему
отношению ![]() . Характерным свойством этого режима является
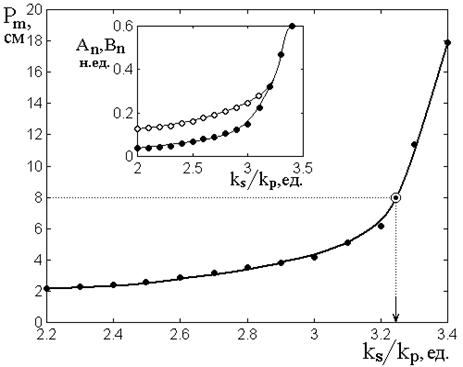
период описывающей его синусоиды. Рассмотрим рис.11, где показана зависимость
периода синусоидальной модуляции от отношения волновых чисел барьера и промежутка
. Характерным свойством этого режима является
период описывающей его синусоиды. Рассмотрим рис.11, где показана зависимость
периода синусоидальной модуляции от отношения волновых чисел барьера и промежутка
![]() .
.
Рис.11. Зависимость периода синусоидальной модуляции от отношения волновых чисел барьера и промежутка.
На врезке – зависимости максимальной амплитуды синусоиды (по половине максимального размаха) от отношения волновых чисел. Сплошные точки – волны прямого направления, открытые – обратного.
Из рисунка видно, что по
мере увеличения этого отношения период увеличивается тем быстрее, чем больше
отношение волновых чисел становится ближе к величине ![]() ,
при которой длина периода сравнивается с полной длиной структуры, в данном
случае равной
,
при которой длина периода сравнивается с полной длиной структуры, в данном
случае равной ![]() . Горизонтальная точечная линия,
упирающаяся в укрупненную точку, соответствует как раз полной длине структуры.
Опущенный из этой точки перпендикуляр на горизонтальную ось приходится на
. Горизонтальная точечная линия,
упирающаяся в укрупненную точку, соответствует как раз полной длине структуры.
Опущенный из этой точки перпендикуляр на горизонтальную ось приходится на ![]() . Можно видеть, что правее этой точки
период еще продолжает увеличиваться, однако теперь уже на длине структуры укладывается
только часть периода.
. Можно видеть, что правее этой точки
период еще продолжает увеличиваться, однако теперь уже на длине структуры укладывается
только часть периода.
На том же рис.11 на
врезке приведены зависимости максимальной амплитуды синусоиды (по половине
максимального размаха) от отношения волновых чисел. Такой максимальный размах
наблюдается где-то вблизи середины структуры. Из рисунка видно, что при ![]() максимальная амплитуда волн обратного
направления превышает такую же амплитуду волн прямого направления приблизительно
в два раза (как это и наблюдается на рис.6), однако при
максимальная амплитуда волн обратного
направления превышает такую же амплитуду волн прямого направления приблизительно
в два раза (как это и наблюдается на рис.6), однако при ![]() амплитуды
волн обоих направлений сравниваются между собой тем точнее, чем отношение
амплитуды
волн обоих направлений сравниваются между собой тем точнее, чем отношение ![]() больше.
больше.
Синусоидальный режим
существует в интервале отношения волновых чисел ![]() .
Нижняя граница этого интервала определяется тем, что период модуляции
приближается к суммарной толщине двух соседствующих слоев, то есть сравнивается
с периодом самой структуры. Верхняя граница соответствует увеличению периода
модуляции выше полной длины структуры, то есть ситуации, когда на длине структуры
период уже не укладывается.
.
Нижняя граница этого интервала определяется тем, что период модуляции
приближается к суммарной толщине двух соседствующих слоев, то есть сравнивается
с периодом самой структуры. Верхняя граница соответствует увеличению периода
модуляции выше полной длины структуры, то есть ситуации, когда на длине структуры
период уже не укладывается.
Эволюция изменения
характера синусоиды при увеличении отношения ![]() состоит
в сдвиге ее по фазе в сторону меньших значений координаты
состоит
в сдвиге ее по фазе в сторону меньших значений координаты ![]() , причем этот сдвиг сопровождается
увеличением величины периода до такой степени, что на всей длине структуры
помещается только один полупериод синусоиды. При этом амплитуда остающегося
полупериода увеличивается настолько, что превышает амплитуду падающей волны
благодаря наступающему пространственному резонансу (на длине структуры укладывается
половина длины волны модуляции). При таком увеличении отношения
, причем этот сдвиг сопровождается
увеличением величины периода до такой степени, что на всей длине структуры
помещается только один полупериод синусоиды. При этом амплитуда остающегося
полупериода увеличивается настолько, что превышает амплитуду падающей волны
благодаря наступающему пространственному резонансу (на длине структуры укладывается
половина длины волны модуляции). При таком увеличении отношения ![]() (то есть выше величины
(то есть выше величины ![]() ) синусоидальный режим сменяется полусинусоидальным,
после чего линейным, а затем экспоненциальным.
) синусоидальный режим сменяется полусинусоидальным,
после чего линейным, а затем экспоненциальным.
Схема такой последовательной смены режимов иллюстрируется рис.12, к рассмотрению которого переходим.
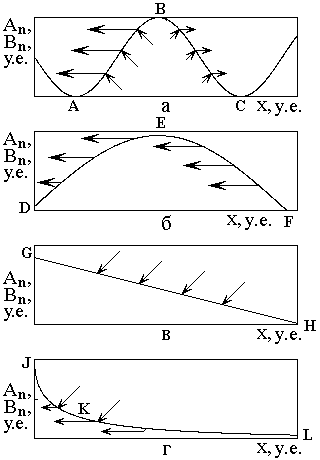
Рис.12. Схема переходов между режимами.
Масштаб не соблюден, единицы по осям – условные.
а – режим синусоидальный; б – режим полусинусоидальный;
в – режим линейный; г – режим экспоненциальный.
Основной общей тенденцией
изменения зависимостей ![]() и
и ![]() при увеличении
при увеличении
![]() является смещение кривых в сторону меньших
значений координаты, то есть влево по рисунку. Стрелками показаны направления
смещения отдельных участков кривых.
является смещение кривых в сторону меньших
значений координаты, то есть влево по рисунку. Стрелками показаны направления
смещения отдельных участков кривых.
В синусоидальном режиме
(а) положительный полупериод синусоиды ABC смещается в левую сторону, одновременно расширяясь.
При этом участок АВ смешается сильнее, чем участок ВС, который от него
несколько отстает. В результате на всем протяжении структуры остается только
один положительный полупериод синусоиды, что соответствует переходу к режиму
полусинусоидальному (б), то есть кривая АВС трансформируется в кривую DEF. Далее вся эта кривая опять
смещается влево с одновременным расширением, в результате чего участок DE уходит за левый край рисунка, а
участок EF, также смещаясь влево,
распрямляется, трансформируясь в прямую линию GH линейного режима (в). Далее участки линии GH продолжают смещаться влево, в
результате чего плоская часть кривой GH проваливается и прямая трансформируется в убывающую экспоненту, то есть
наступает экспоненциальный режим (г). При дальнейшем увеличении отношения ![]() участок экспоненты JK стремится к вертикальной оси, а
участок KL – к горизонтальной, то есть
показатель экспоненты постепенно увеличивается.
участок экспоненты JK стремится к вертикальной оси, а
участок KL – к горизонтальной, то есть
показатель экспоненты постепенно увеличивается.
Более подробное
рассмотрение описанного поведения приведенных зависимостей показало, что рост
амплитуды при увеличении ![]() , отмеченный на врезке
в рис.11 имеет место только до того момента, когда синусоидальный режим полностью
перейдет в полусинусоидальный, после чего при дальнейшем увеличении
, отмеченный на врезке
в рис.11 имеет место только до того момента, когда синусоидальный режим полностью
перейдет в полусинусоидальный, после чего при дальнейшем увеличении ![]() амплитуды колебаний в слоях спадают.
Такой спад амплитуды объясняется выходом системы из условий отмеченного выше
пространственного резонанса. Заметим, что, несмотря на отсутствие затухания в
данном рассмотрении, амплитуда колебаний при пространственном резонансе
остается конечной, что наводит на мысль об аналогии рассматриваемых явлений с колебаниями
закрепленной на концах механической струны.
амплитуды колебаний в слоях спадают.
Такой спад амплитуды объясняется выходом системы из условий отмеченного выше
пространственного резонанса. Заметим, что, несмотря на отсутствие затухания в
данном рассмотрении, амплитуда колебаний при пространственном резонансе
остается конечной, что наводит на мысль об аналогии рассматриваемых явлений с колебаниями
закрепленной на концах механической струны.
Замечание. Заметим, что в условиях настоящего исследования распространения такой аналогии на моды выше первой обнаружено не было, то есть явно выраженные пространственные резонансы при укладывании на длине структуры двух и более полуволн не наблюдались. Возможной причиной такого обстоятельства может быть недостаточное число слоев, составляющих структуру (здесь – шестнадцать). При этом форма пространственной моды, в отличие от непрерывной струны, где она плавная, здесь получается ступенчатой, причем узлы стоячих мод могут приходиться на внутренние участки ступенек, то есть синусоидальная структура мод получается как бы состоящей из «крупных клеток», затрудняющих точную идентификацию. Таким образом, в качестве рекомендации для обнаружения пространственных мод более высоких порядков можно указать на необходимость увеличения числа слоев структуры хотя бы до нескольких десятков.
17. Структура областей существования режимов по волновому числу
Описанные переходы между
режимами хорошо наблюдается при ![]() . При
. При ![]() переходы между режимами №4 и №5 также
являются плавными и происходят через посредство режимов №2 и №3 в прямом или
обратном порядке, однако интервалы этих переходов становятся крайне узкими, не
более
переходы между режимами №4 и №5 также
являются плавными и происходят через посредство режимов №2 и №3 в прямом или
обратном порядке, однако интервалы этих переходов становятся крайне узкими, не
более ![]() , причем по мере увеличения отношения
, причем по мере увеличения отношения ![]() далее сужаются. Рассмотрим чередование
режимов №4 и №5 при увеличении
далее сужаются. Рассмотрим чередование
режимов №4 и №5 при увеличении ![]() более подробно.
более подробно.
18. Отражающие свойства структуры
Естественно предположить, что при увеличении различия между волновыми числами составляющих структуру слоев, отражение от структуры в целом должно увеличиваться, так как ее неоднородность при этом возрастает.
Поэтому сначала обратимся
к волне обратного направления ![]() в слое №1, характеризующей
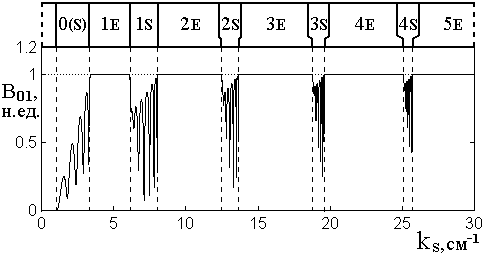
отражающие свойства структуры в целом. Для этого рассмотрим рис.13, где
показана зависимость амплитуды волны обратного направления
в слое №1, характеризующей
отражающие свойства структуры в целом. Для этого рассмотрим рис.13, где
показана зависимость амплитуды волны обратного направления ![]() от волнового числа
от волнового числа ![]() при
при
![]() .
.
Из
рисунка видно, что на упомянутой зависимости действительно имеются довольно
широкие области, где ![]() , то есть волна от структуры полностью
отражается. Эти области обозначены как 1Е, 2Е, 3Е и так далее, где цифра
обозначает порядковый номер области, а буква «Е» – экспоненциальный характер
распределения амплитуды по слоям структуры, то есть режим №4.
, то есть волна от структуры полностью
отражается. Эти области обозначены как 1Е, 2Е, 3Е и так далее, где цифра
обозначает порядковый номер области, а буква «Е» – экспоненциальный характер
распределения амплитуды по слоям структуры, то есть режим №4.
Рис.13. Зависимость амплитуды волны
обратного направления в слое №1 от волнового числа ![]() при
при ![]() .
.
Полная длина структуры – ![]() , толщины слоев –
, толщины слоев – ![]() ,
число слоев –
,
число слоев – ![]() .
.
В верхнем ряду – схема расположения
областей существования по волновому числу ![]() режимов
экспоненциального (Е) и синусоидального (S).
режимов
экспоненциального (Е) и синусоидального (S).
Однако наряду с областями
полного отражения имеются области, где ![]() значительно
уменьшается, причем зависимость
значительно
уменьшается, причем зависимость ![]() от
от ![]() имеет осциллирующий характер. Эти области
обозначены как 1S, 2S, 3S, . . . , где цифра означает порядковый номер области, а
буква «S» – синусоидальный с верхним пределом
характер распределения амплитуды по слоям структуры, то есть режим №5.
имеет осциллирующий характер. Эти области
обозначены как 1S, 2S, 3S, . . . , где цифра означает порядковый номер области, а
буква «S» – синусоидальный с верхним пределом
характер распределения амплитуды по слоям структуры, то есть режим №5.
Малым значениям волнового
числа ![]() соответствует область 0(S), где характер распределения
амплитуд является синусоидальным, но верхнего предела не имеет, что
соответствует режиму №1.
соответствует область 0(S), где характер распределения
амплитуд является синусоидальным, но верхнего предела не имеет, что
соответствует режиму №1.
Начала областей
синусоидального режима соответствуют следующим волновым числам: 1S – ![]() ; 2S –
; 2S – ![]() ; 3S –
; 3S – ![]() ; 4S –
; 4S – ![]() , то
есть выполняется соотношение
, то
есть выполняется соотношение ![]() , где
, где ![]() – номер соответствующей области.
– номер соответствующей области.
Можно полагать, что
существование подобных чередующихся областей связано с пространственным
резонансом волны на длине слоя. То есть синусоидальный ражим №5 наступает
тогда, когда на толщине слоя укладывается половина длины волны. Действительно,
при толщине слоя ![]() , если полагать, что эта толщина
соответствует половине длины волны, то полная длина волны равна
, если полагать, что эта толщина
соответствует половине длины волны, то полная длина волны равна ![]() , то есть волновое число при этом равно:
, то есть волновое число при этом равно: ![]() , что как раз соответствует волновому
числу
, что как раз соответствует волновому
числу ![]() в начале области 1S. Если на толщине слоя укладывается
две полуволны, то
в начале области 1S. Если на толщине слоя укладывается
две полуволны, то ![]() , что соответствует
, что соответствует ![]() , то есть
, то есть ![]() в
начале области 2S. Следующая
область 3S соответствует укладыванию на толщине
слоя трех полуволн и так далее.
в
начале области 2S. Следующая
область 3S соответствует укладыванию на толщине
слоя трех полуволн и так далее.
Заметим, что речь идет о
тех слоях структуры, где волновое число равно именно ![]() ,
так как в других слоях волновое число
,
так как в других слоях волновое число ![]() –
другое, то есть резонанс в этих слоях не возбуждается. При этом, в силу геометрии
задачи, слои, где волновое число равно
–
другое, то есть резонанс в этих слоях не возбуждается. При этом, в силу геометрии
задачи, слои, где волновое число равно ![]() , имеют
четные номера, а слои, где волновое число равно
, имеют
четные номера, а слои, где волновое число равно ![]() –
нечетные. То есть резонансными слоями являются именно четные, а нечетные
являются лишь связующими звеньями между резонансными. То есть структура в целом
представляет собой многорезонаторную систему, состоящую из цепочки резонаторов,
связанных нерезонансными звеньями.
–
нечетные. То есть резонансными слоями являются именно четные, а нечетные
являются лишь связующими звеньями между резонансными. То есть структура в целом
представляет собой многорезонаторную систему, состоящую из цепочки резонаторов,
связанных нерезонансными звеньями.
Осциллирующий характер
зависимостей амплитуды волны ![]() от
от ![]() внутри резонансных областей 1S, 2S, 3S и
так далее, по-видимому, обусловлен взаимодействием связанных колебаний в
соседних слоях структуры, обладающих одинаковыми резонансными свойствами, то
есть имеет место расщепление общей резонансной кривой, свойственное
многорезонаторной системе.
внутри резонансных областей 1S, 2S, 3S и
так далее, по-видимому, обусловлен взаимодействием связанных колебаний в
соседних слоях структуры, обладающих одинаковыми резонансными свойствами, то
есть имеет место расщепление общей резонансной кривой, свойственное
многорезонаторной системе.
Наблюдаемое сужение
резонансных областей по мере увеличения ![]() ,
по-видимому, связано с уменьшением эффективности возбуждения резонансных мод по
мере увеличения их номера (с уменьшением «интеграла перекрытия»).
,
по-видимому, связано с уменьшением эффективности возбуждения резонансных мод по
мере увеличения их номера (с уменьшением «интеграла перекрытия»).
Таким образом, отражающие свойства рассматриваемой многослойной структуры подобны свойствам классической многорезонаторной системы, где роль частоты играет волновое число, в результате чего частотный резонанс проявляется как пространственный резонанс по координате.
Отметим, что в отличие от классического резонанса, предполагающего высокую амплитуду в резонансных условиях, здесь при выполнении условий резонанса, то есть равенства целого числа полуволн толщине слоя, амплитуда в резонансных слоях (четных) получается меньшей, чем в нерезонансных (нечетных), что в той или иной степени наблюдается во всех режимах. Таким образом, резонансный слой как бы «выталкивает из себя» энергию колебаний, то есть благодаря кратности своей длины целому числу полуволн, при попадании в него распространяющейся волны, стремится передать эту энергию дальше, не накапливая ее в себе самом.
19. Пропускающие свойства структуры
Обратимся теперь к
рассмотрению пропускающих свойств той же структуры. При рассмотрении рис.10 уже
отмечалась сильно различающаяся роль четности и нечетности номера слоя. Так
амплитуды волн прямого направления в двух последних слоях равны: ![]() ,
, ![]() , то
есть отличаются на порядок. Поэтому далее рассмотрим поведение амплитуд
указанных волн в обоих этих слоях, иллюстрируемое рис.14.
, то
есть отличаются на порядок. Поэтому далее рассмотрим поведение амплитуд
указанных волн в обоих этих слоях, иллюстрируемое рис.14.
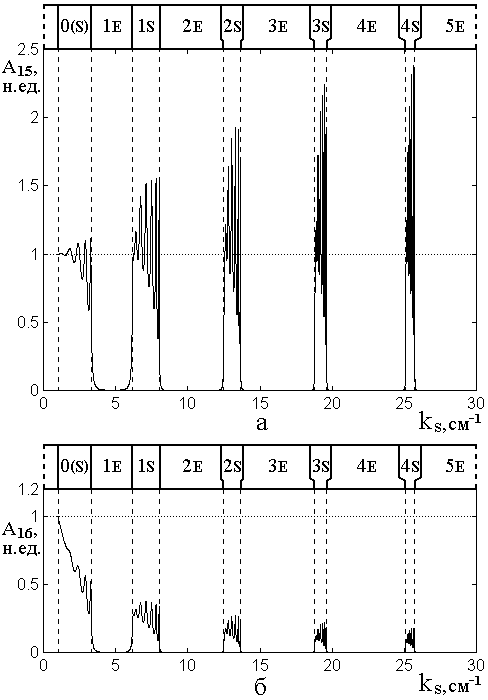
Рис.14. Зависимости амплитуд волн
прямого направления в слоях №15 (а) и №16 (б) от волнового числа ![]() при
при ![]() .
.
Все параметры совпадают с приведенными на предыдущем рисунке.
Из рисунка видно, что общая структура по волновому числу границ областей максимумов амплитуды прямых волн для обоих слоев совпадает со структурой минимумов обратных волн для слоя №1, приведенной на рис.13.
То есть, при тех значениях волнового числа, где в слое №1 наблюдается уменьшение амплитуды, здесь в слоях №15 и 16 наблюдается ее увеличение. В этих интервалах волнового числа имеет место соответственно режим №5 – синусоидальный с верхним пределом. Между этими интервалами имеет место режим №4 – экспоненциальный со спадом амплитуды по координате, при котором амплитуды волн в слоях №15 и 16 близки к нулю.
В областях существования
режима №5 амплитуда волн в слое №15, всегда будучи большей единицы, по мере
увеличения ![]() возрастает, тогда как в слое №16, будучи
меньшей единицы, соответственно убывает. Так в области 1S при
возрастает, тогда как в слое №16, будучи
меньшей единицы, соответственно убывает. Так в области 1S при ![]() амплитуда
амплитуда
![]() составляет около
составляет около ![]() ,
а амплитуда
,
а амплитуда ![]() –
– ![]() , тогда
как в области 4S при
, тогда
как в области 4S при ![]() эти же величины соответственно равны:
эти же величины соответственно равны: ![]() и
и ![]() То
есть с увеличением волнового числа различие между амплитудами в соседствующих
слоях растет.
То
есть с увеличением волнового числа различие между амплитудами в соседствующих
слоях растет.
Резонансным размером здесь обладает слой №16 (четный), так что можно полагать, что по мере увеличения числа укладывающихся на его длине полуволн, условия резонанса становятся более критичными, то есть резонансная линия сужается, вызывая соответствующее усиление свойства «выталкивания» энергии из резонансного слоя, отмеченного при разборе рис.13. Такое «выталкивание» и приводит к уменьшению амплитуды в слое №16 с соответствующим увеличением в слое №15.
Тонкая
структура изрезанности рассматриваемых зависимостей в областях существования
режима №4, надо полагать, обусловлена теми же причинами, что и подобная
структура для волны ![]() , то есть расщеплением резонансной
характеристики за счет сильной связи нескольких резонаторов в многорезонаторной
системе.
, то есть расщеплением резонансной
характеристики за счет сильной связи нескольких резонаторов в многорезонаторной
системе.
20. Замечание о частотных свойствах структур с периодическими неоднородностями
Здесь рассмотрены зависимости амплитуд волн обоих направлений от волнового числа, что не ограничивает общности задачи в том плане, что ее решение с частотой волны напрямую никак не связано. В то же время, как известно (см. напр.[33] и множество других учебников), волновое число волны, распространяющейся в какой-то среде, связано с частотой той же волны дисперсионным соотношением, которое в общем случае является нелинейным.
Однако в частном случае сред с линейной дисперсией, волновое число и частота прямо пропорциональны друг другу, в результате чего зависимости, полностью подобные показанным на рис.2-6, будут не только от волнового числа, но также и от частоты, что может быть особенно важным для построения частотноселективных систем.
Заключение
Рассмотрено распространение волн прямого и обратного направлений в структуре ограниченной длины с периодической неоднородностью меандрового вида. Получены амплитуды волн в крайних слоях структуры. Показано, что амплитуды волн как прямого, так и обратного направлений распространения имеют ярко выраженные особенности в случае, когда на длине периода структуры укладывается одна половина длины волны. По обе стороны от главного максимума обнаружены осцилляции, обусловленные интерференционными явлениями за счет конечности общего числа барьеров структуры, причем при увеличении количества барьеров амплитуды осцилляций уменьшаются, а главный максимум сужается.
Выявлен эффект «вторичной модуляции», состоящий в периодической осцилляции амплитуд отраженной и проходящей волн при изменении среднего волнового числа. Высказано предположение, что причиной вторичной модуляции является чередование пространственных резонаторов, образованных периодически повторяющимися участками структуры с различными свойствами.
Исследованы амплитуды волн прямого и обратного направлений при изменении координаты или номера слоя структуры, а также среднего волнового числа. Выявлен монотонно спадающий характер амплитуды волн обратного направления в сочетании с осциллирующим спадом амплитуды волн прямого направления, объясненный сочетанием постепенного просачивания волны через структуру с убыванием энергии волны в полосе непропускания и сохранением ее энергии вне такой полосы.
Рассмотрено распространение волн в условиях неоднородности пилообразного вида, в том числе влияние структуры зубца «пилы». Показано, что пилообразная неоднородность на амплитудах распространяющихся волн сказывается значительно слабее, чем меандровая (приблизительно в полтора-два раза), причем тонкая структура «зубца» пилы проявляется тем слабее, чем ближе его длина приближается к длине барьера меандра.
Рассмотрено распределение амплитуд в случае большого (до нескольких раз) изменения соотношения между волновыми числами двух видов сред, составляющих структуру.
На основе периодической структуры в виде симметричного меандра выявлена сильная зависимость распределения амплитуд в слоях от координаты, соответствующей продольному размеру структуры, интерпретированная как пространственная модуляция амплитуды.
В характере пространственной модуляции выявлены пять основных режимов: синусоидальный, полусинусоидальный, линейный, экспоненциальный и синусоидальный с верхним пределом. Показано, что по мере увеличения отношения волновых чисел в слоях того и другого вида эти режимы сменяют друг друга последовательно. При этом основными режимами являются синусоидальный и экспоненциальный, интервалы существования которых значительно (в несколько раз) превышают интервалы существования режимов линейного и полусинусоидального, которые по существу являются переходными между двумя основными.
Полусинусоидальный режим интерпретирован как соответствующий резонансу, при котором на полной длине структуры укладывается половина длины волны пространственной модуляции амплитуды.
Синусоидальный режим с верхним пределом интерпретирован как соответствующий резонансу, при котором на толщине одного слоя укладывается целое число полуволн распространяющейся волны. При этом на зависимости амплитуд волн от большего волнового числа из двух видов слоев имеет место периодическое расположение областей упомянутого режима.
Показано, что такая зависимость имеет вид широких областей экспоненциального режима, перемежающихся периодически расположенными узкими областями синусоидального режима с верхним пределом, причем соотношение протяженностей областей, соответствующих этим двум режимам, может достигать нескольких раз и увеличивается по мере увеличения волнового числа. Отмечено, что зависимость амплитуд от волнового числа в областях синусоидального режима с верхним пределом имеет осциллирующий характер.
На основе рассмотрения распространения волн прямого и обратного направлений в отдельных слоях исследованы отражающие и пропускающие свойства структуры в целом. Показано, что в областях экспоненциального режима структура практически полностью отражает падающую волну. В областях синусоидального режима с верхним пределом отражение падает до нескольких раз, а пропускание волны в случае нечетного числа слоев может приближаться к полному, тогда в случае четного уменьшается относительно амплитуды падающей волны почти на порядок.
В качестве возможного объяснения наблюдаемых особенностей пространственной модуляции амплитуды волн в слоях многослойной структуры предложена аналогия с многорезонаторной системой, представляющей собой цепочку последовательно соединенных связанных резонаторов.
Рассмотренные свойства многослойных структур обобщены на случай линейной дисперсии волн. Дана рекомендация использования исследованных структур для построения частотноселективных систем.
Работа выполнена при финансовой поддержке за счет гранта Российского Научного Фонда (проект № 14-22-00279).
Литература
1. Бреховских Л.М. Волны в слоистых средах. М.: Наука. 1973.
2. Бреховских Л.М., Годин О.А. Акустика слоистых сред. М.: Наука. 1989.
3. Розенберг Г.В. Оптика тонкослойных покрытий. М.: Гос.изд.физ-мат.лит. 1958.
4. Кизель В.А. Отражение света. М.: Наука. 1973.
5. Oksanen M.I., Hanninen J., Tretyakov S.A. // IEEE Proc.H. 1991. V.138. №7. P.513.
6. Шварцбург А.Б. // УФН. 2000. Т.170. №12. С.1297.
7. Бриллюэн Л., Пароди М. Распространение волн в периодических структурах. М.: ИЛ. 1959.
8. Кирюхин Н.Н., Лисовский Ф.В. // ФТТ. 1968. Т.10. №3. С.709.
9. Зубков В.И., Моносов Я.А., Щеглов В.И. // Письма в ЖЭТФ. 1971. Т.13. №5. С.229.
10. Медников А.М., Никитов С.А., Попков А.Ф. // ФТТ. 1982. Т.24. №10. С.3008.
11. Герус С.В., Харитонов В.Д. // ФММ. 1984. Т.58. №6. С.1069.
12. Вороненко А.В., Герус С.В., Харитонов В.Д. // Изв. ВУЗов. Физика. 1988. Т.31. №11. С.76.
13. Анненков А.Ю., Герус С.В. // РЭ. 1996. Т.41. №2. С.216.
14. Бутько Л.Н., Бучельников В.Д., Бычков И.В., Шавров В.Г. // Журнал радиоэлектроники [электронный журнал]. 2007. №3. URL:
http://jre.cplire.ru/jre/mar07/3/text.html
15. Уиттекер Э.Т., Ватсон Д.Н. Курс современного анализа. Ч.2. М.: ИЛ. 1963.
16. Мак-Лахлан Н.В. Теория и приложения функций Матье. М.: ИЛ. 1953.
17. Флюгге З. Задачи по квантовой механике. Т.1. М.: МИР. 1974.
18. Борн М., Вольф Э. Основы оптики. М.: Наука. 1970.
19. Антонец И.В., Щеглов В.И. Распространение волн через многослойные структуры. Часть первая. Прямой метод. Сыктывкар: ИПО СыктГУ. 2011.
20. Антонец И.В., Щеглов В.И. Распространение волн через многослойные структуры. Часть вторая. Метод матрицы. Сыктывкар: ИПО СыктГУ. 2012.
21. Антонец И.В., Щеглов В.И. Распространение волн через многослойные структуры. Часть третья. Метод импеданса. Сыктывкар: ИПО СыктГУ. 2012.
22. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2012. Т.57. №1. С.67.
23. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2013. Т.58. №1. С.16.
24. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // Журнал радиоэлектроники [электронный журнал]. 2013. №1. URL:
http://jre.cplire.ru/jre/jan13/11/text.pdf
25. Антонец И.В., Щеглов В.И. Алгоритмы определения амплитуд отраженных и проходящих волн при распространении встречных волн в многослойных неоднородных структурах. Часть первая. Укороченный алгоритм. Учебное пособие (электронное). Сыктывкар: ИПО ФГБОУ ВПО СыктГУ. 2013.
26. Антонец И.В., Щеглов В.И. Алгоритмы определения амплитуд отраженных и проходящих волн при распространении встречных волн в многослойных неоднородных структурах. Часть вторая. Полный алгоритм. Учебное пособие (электронное). Сыктывкар: ИПО ФГБОУ ВПО СыктГУ. 2013.
27. Антонец И.В., Щеглов В.И. Распространение волн через многослойные структуры (монография). Часть пятая. Алгоритмические методы. Сыктывкар: ИПО СыктГУ. 2014.
28. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // Журнал радиоэлектроники [электронный журнал]. 2013. №4. URL:
http://jre.cplire.ru/jre/apr13/6/text.pdf
29. Антонец И.В., Шавров В.Г., Щеглов В.И. // РЭ. 2013. Т.58. №12. С.1149.
30. Антонец И.В., Шавров В.Г., Щеглов В.И. // Сборник трудов XXI Международной конференции «Электромагнитное поле и материалы». Москва, МЭИ: «НИУ МЭИ». 2013. С.130.
31. Антонец И.В., Шавров В.Г., Щеглов В.И. // Сборник трудов XXI Международной конференции «Электромагнитное поле и материалы». Москва, МЭИ: «НИУ МЭИ». 2013. С.145.
32. Антонец И.В., Щеглов В.И. Распространение волн через многослойные структуры (монография). Часть четвертая. Специфические методы. Сыктывкар: ИПО СыктГУ. 2013.
33. Карлов Н.В., Кириченко Н.А. Колебания, волны, структуры. М.: ФИЗМАТЛИТ. 2003.
34. Антонец И.В., Шавров В.Г., Щеглов В.И. // Сборник трудов XXII Международной конференции «Электромагнитное поле и материалы», Москва, МЭИ: «НИУ МЭИ». 2014. С.124.