УДК 621.385.69;621.385.19
ОБ ОДНОМ РЕЖИМЕ ГЕНЕРАЦИИ В ОРОТРОНЕ С ДВУХРЯДНОЙ ПЕРИОДИЧЕСКОЙ СТРУКТУРОЙ ТЕРАГЕРЦОВОГО ДИАПАЗОНА
Е. А. Мясин1, Ю. В. Андреев2, В. В. Евдокимов1, А. Ю. Ильин1
1 Фрязинский филиал ИРЭ им. В.А.Котельникова РАН
2 ИРЭ им. В.А.Котельникова РАН, Москва
Статья получена 16 февраля 2015 г.
Аннотация. В результате математического моделирования электронно - волнового взаимодействия в оротроне с двухрядной периодической структурой впервые обнаружена возможность существования двух режимов стационарной генерации, один из которых никогда ранее не исследовался. Он характеризуется малой величиной электронного КПД при малой напряжённости высокочастотного (ВЧ) поля в открытом резонаторе (ОР), наряду с известным стационарным режимом генерации при большей напряжённости ВЧ поля в ОР и большей величине электронного КПД. Существование этого режима подтверждено экспериментом.
Ключевые слова: оротрон, двухрядная периодическая структура, открытый резонатор, миллиметровый диапазон волн.
Abstract. As a result of computer simulation of electron-wave interaction in the orotron with double-row periodic structure the possibility of existence of two stationary generation regimes has been found. One of those regime was never explored before. It is characterized by low value of electron efficiency when the high frequency electric field intensity in open resonator is low, while the well-known stationary generation regime occurs when these parameters are high enough. The experimental verification of a new regime is presented.
Key words: orotron, double-row periodic structure, open resonator, millimeter wavelength range.
Введение
Несмотря на заметный прогресс в освоении низкочастотной части терагерцового диапазона вплоть до 1.5 ТГц (или длинноволновой части субмиллиметрового диапазона вплоть до 0.2мм) классическими приборами О – типа (ЛОВ - генераторами), задача увеличения мощности генерируемого излучения приборами О – типа остаётся актуальной. В этой связи оротрон с двухрядной периодической структурой (ДРПС) мог бы оказаться весьма подходящим прибором для достижения этой цели, так как исследования работы этого прибора в 3-миллиметровом диапазоне волн показали возможность получения относительно большого КПД (6%) и большой мощности (³ 1кВт) в импульсном режиме при напряжении 20кВ [1]. Однако для достижения такого результата при создании прибора должны быть выполнены определённые условия [2]: 1) длина ДРПС = (4-5) rк, где rк - радиус каустики на плоском зеркале открытого резонатора (ОР) в 2-3 раза больше длины волны; 2) расстояние между зеркалами резонатора HОР £ 10 мм; 3)отношение периода l к высоте 2H пролётного канала ³ 3; 4) ширина электронного потока 2С £ rк. Выполнение условий 3) и 4) позволяет не учитывать неоднородность ВЧ поля по ширине и толщине электронного потока. Так как rк = Ö(l/pÖ HОР (R - HОР)), то по мере уменьшения длины волны уменьшается rк и, как следствие, ширина электронного потока, а значит и генерируемая ВЧ мощность. Кроме того, если принять за максимально возможное напряжение U = 20кВ, то, например, для l =1мм период будет 0.27мм и, чтобы выполнить условие 3), пролётный канал должен быть 0.07мм, а для генерации на длине волны 0.8мм – период l = 0.21мм, пролётный канал 0.05мм и т.д. На практике реализовать эти условия чрезвычайно сложно.
Поэтому приходится идти на нарушение условия 3) и мириться с тем, что отношение l/2H < 3. Но в этом случае ухудшается эффективность электронно-волнового взаимодействия и возрастает пусковой ток, поэтому может оказаться, что нельзя выполнить условие 1). В этом случае приходится увеличивать длину пространства взаимодействия, и длина ДРПС может быть увеличена до 10 rк и более [3]. Тем не менее, для генерации относительно длинноволнового излучения, например, для l =1.3мм (~230ГГц), весьма заманчиво использовать ДРПС длиной 5rк, выполнив также условие 3).
В работе [4] на основе приближённой аналитической теории [5] была проведена оптимизация электронно - волнового взаимодействия в оротроне для генерации на длине волны для l =1.3мм. Для оротрона с «короткой» (5 радиусов каустики) ДРПС и ОР со сферическим фокусирующим зеркалом проведен расчёт геометрических и энергетических характеристик прибора с ДРПС, имеющей период 0,29 мм. Выяснены основные закономерности влияния различных параметров на эффективность взаимодействия электронного потока с ВЧ полем ДРПС. Показано, что при определённых условиях оротрон с ДРПС может генерировать на длине волны 1,3 мм мощность, выводимую в нагрузку, в десятки Ватт. Однако, может оказаться, что эти условия реализовать не представляется возможным, и тогда мощность, выводимая в нагрузку, будет существенно меньше (порядка единиц Ватта или даже меньше) [4].
Теория
В этой связи необходимо было исследовать оптимизацию параметров оротрона более детально на основе точных, а не приближённых уравнений нелинейной теории той же работы [5].
Самосогласованное решение нелинейной теории электронно-волнового взаимодействия в оротроне получается в результате совместного решения системы уравнений: нелинейного уравнения движения и уравнения возбуждения, а также решения уравнения обмена энергией в ОР прибора. Самосогласованное решение задачи может быть представлено как точка пересечения зависимости электронного КПД he_1(F0) от безразмерной напряжённости поля F0, полученной в результате решения нелинейной системы уравнений, с зависимостью электронного КПД he_2(F0), полученного в результате решения уравнения обмена энергией в ОР.
Для нахождения электронного КПД в результате решения уравнения движения и возбуждения [5] необходимо вычислить двойной интеграл
he_1 = - (L1F0/p)0ò1 f(y) [0ò2pcos( Ф - jy)dj0] dy, где (1)
f(y) =exp[-m2(y-0,5)2], m = L0/rк, rк - радиус каустики,
а величина фазы Ф найдена в результате решения уравнения движения [2]:
d2Ф/dy2 = - m [1 + 1/L1 (dФ/dy)]3 f (y) cos(Ф - jy), где (2)
y = z/L0; Ф = (w t -be z); L1 =be L0; F0 = (E0c)/(2beU0); be=w /V0; j =bL1; b=V0/Vф-1; m = (L1)2F0; c = E1/E0 – отношение амплитуды рабочей гармоники ВЧ поля к амплитуде объёмного поля в ОР. При y = 0; Ф =j0; dФ / dy = 0.
Из уравнения обмена энергией в ОР электронный КПД находится по формуле [5]:
he_2 = (135/pc2)(F0)2, где (3)
p = qнI0/na2, a = rк/l; qн – нагруженная добротность в 1000; I0 – рабочий ток; n – число полуволн между зеркалами ОР.
Уравнения нелинейной теории работы [5] были решены в среде Math lab. Для представления электронного потока использовался метод «крупных частиц», число которых на период колебания было равно 50. Нелинейное уравнение движения, преобразованное в дифференциальное уравнение второго порядка для фазы колебания в системе координат, связанной с электронным потоком, решалось методом Рунге – Кутта 4,5 порядка. Интеграл в выражении (1) вычислялся методом Симпсона.
Результат вычислений зависимостей по формулам (1) и (3) представлялся графически в виде двух функций, соответственно he_1(F0) и he_2(F0), а точки их пересечения вычислялись численно путем нахождения нулей разностной функции he_1(F0) – he_2(F0). Эти точки пересечения представляют режимы стационарных состояний генерации в оротроне, о чём уже говорилось ранее.
Поведение этого решения исследовалось для различных параметров, путём моделирования на компьютере для длины волны l =1.3мм. Использовались те же физические параметры, что и в работе [4] для решения этой задачи на основе приближённой аналитической теории. Таким образом, в оротроне используется полусферический открытый резонатор (ОР) с радиусом каустики на плоском зеркале rк = 3l = 3.9 мм, длина ДРПС L0 = 5 rк = 19.5мм, период l = 0.29мм, отношение щели d к периоду l d /l = 0,5, замедление nф = с/ Vф = l/ l » 4.48.
Собственная добротность Q0 для ДРПС: Q0 = 2HОР/ d(4 +l/l) =ln/d(4 +l/l), где n – число полуволн основного типа колебаний ТЕМ00n между зеркалами ОР. Задав n = 15, будем иметь Q0 » 16000. Однако, как следует из опыта, реальная добротность оказывается обычно в 1.5 - 2 раза меньшей величины. Поэтому полагаем Q0 » 8000. HОР = 9.75 мм. Rсф = 148мм.
Введём безразмерные переменные, необходимые для расчёта, задав значения параметра несинхронности b = 0.05, 0.04, 0.03, 0.02:
b1 = 0.05;, L1 = be L0 = (2p/l) [nф /(1+ b1)] L0 » 402; m = L0/rк = 5; a = rк/l= 3, отношение амплитуды рабочей гармоники E1 к амплитуде E0 ВЧ поля в ОР c = E1/E0 = 0.3,.., 0,637; нагруженная добротность Qн в 1000 qн = 1,.., 4, рабочий ток I0 = 0.15... 0.4 А, n = 15-17. Отметим, что при выбранных геометрических размерах физической длины L0 ДРПС и ОР параметры m = 5, a = 3 постоянны.
Прежде всего, исследуем поведение КПД от параметра несинхронности при некотором наборе других параметров. Итак, b1 = 0.05, L0 » 402, m = 5, a =3, qн = 4 при Q0 » 8000 обеспечивает КПД ОР 0.5. Возьмём максимальную величину c = 0,637, соответствующую четвертьволновому резонансу в ОР, n = 15, а варьировать будем величину рабочего тока в пределах I0 = 0.15… 0.4А.
Результат решения (1) на компьютере, представленный на Рис.1, даёт зависимость he-1 = f(F0) кривой 1, а результат решения (3) параболой he-2 = f(F02) кривой 2. Точки пересечения этих двух кривых являются решением системы уравнений и определяют стационарное состояние генерации при достижении безразмерной напряжённостью ВЧ поля F0 величины, соответствующей абсциссам этих точек пересечения.
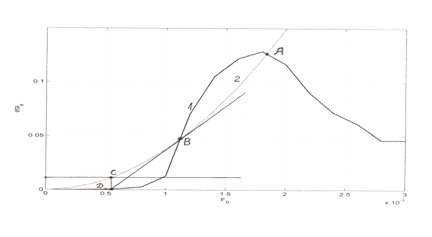
Рис.1
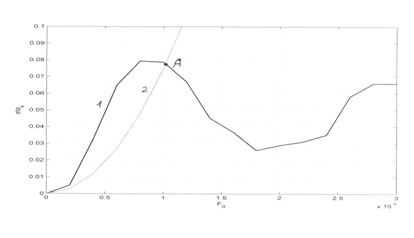
Рис.2
Прежде всего, сравним вид решения для электронного КПД по формуле (1) для параметров несинхронности b1 = 0.05, L0 » 402 (Рис.1) и b2 = 0.03, L0 » 410 (Рис.2) для одних и тех же значений всех параметров, кроме тока. На Рис.1 ток I0 = 0.3А, а на Рис.2 - I0 = 0.15А.
Из сравнения рисунков 1 и 2 следует, что при b1 = 0.05 максимальное значение КПД достигается при большей величине ВЧ – поля F0, чем при b2 = 0.03. Кроме того, при b1 = 0.05 отличная от нуля величина КПД появляется также при значительной величине ВЧ поля F0, в то время как для b2 = 0.03 нарастание КПД происходит практически от нулевых значений ВЧ поля F0. Поэтому, даже при малой величине тока 0.15А, в случае b2 = 0.03 имеется всего одна точка (т. А) пересечения двух кривых, в то время как для тех же значений других параметров в случае b1 = 0.05 – их две. Одна т. В – соответствует малой величине КПД и ВЧ – поля F0, вторая т. А – большим значениям того и другого.
Рассмотрим вопрос о зависимости стационарного режима генерации от тока, вытекающей из (3). Как видно из (3), he ~(F0)2/I0, т.е. электронный КПД уменьшается с ростом тока. При этом поведение точек пересечения на Рис.1 будет обусловлено смещением параболы в сторону больших значений F0. Поэтому точка B пересечения с более низким КПД сместится в сторону меньших значений F0, а т. А с более высоким – в сторону больших значений F0. К чему это должно приводить? Рассмотрим вопрос о пусковом токе для каждого положения точек пересечения на Рис.1. Очевидно, что он должен соответствовать некоторому меньшему значению F0, которому соответствует некоторое меньшее значение he-2. Так как he-2 ~ (F0)2 /I0, то это меньшее значение при фиксированном значении F0 определяется точкой D пересечения оси абсцисс на Рис.1 с касательной, проведенной к параболе в точке B пересечения её с кривой 1. Электронный КПД, соответствующий пусковому режиму, определяется точкой C пересечения перпендикуляра, восстановленного из этой точки, до пересечения с параболой he-2 ~ (F0)2.
Теперь не трудно проанализировать изменение режима генерации при увеличении тока для обоих стационарных режимов Рис.1. Итак, для стационарного состояния, представляемого точкой B пересечения с малым электронным КПД при увеличении рабочего тока мощность генерации сначала из-за роста тока возрастает. Но электронный КПД уменьшается. Эта точка стационарного режима постепенно будет смещаться вниз и пересечёт, в конце концов, горизонтальную линию, проходящую через точку С и соответствующую he пускового режима (тока). Поэтому генерация должна прекратиться.
Для стационарного состояния, представляемого точкой A пересечения he-2 ~(F0)2 с большим электронным КПД, с увеличением рабочего тока она будет смещаться за максимум в сторону увеличения F0, т.е. КПД будет плавно уменьшаться, а мощность генерации также будет возрастать. Но, в отличие от стационарного состояния с малым КПД, для пересечения с линией пускового тока в случае этого стационарного состояния необходимо настолько сильное его увеличение, что реализовать эту ситуацию невозможно. Поэтому, несмотря на увеличение тока и падения КПД, увеличение генерируемой мощности будет происходить без срыва генерации. Это обычно наблюдается в эксперименте, когда выполнены условия для эффективной генерации в оротроне с ДРПС. Для реализации режима генерации, соответствующего точке B пересечения с малым he, достаточно не выполнить эти условия, т.е. чтобы в приборе напряжённость ВЧ поля F0 в ОР была мала.
Эксперимент
На основе проведенного теоретического рассмотрения была разработана и создана электродинамическая система оротрона с короткой (20.6мм) ДРПС и с полусферическим открытым резонатором (ОР) при радиусе кривизны сферы 170мм. ДРПС имела период l = 0.29мм, высоту рядов по 0.24мм, переменную высоту пролётного канала 2H = 0.1мм и 0.15мм. Отметим, что отношение периода к высоте пролётного канала l/2H для высоты пролётного канала 0.1мм чуть меньше 3 (2.9) и близко к значению, являющемуся границей, ниже которой уже нельзя пренебрегать неоднородностью поля по высоте пролётного канала [2]. Для высоты пролётного канала 0.15мм это отношение уже чуть меньше 2 (1.93) и по этой причине эффективность электронно-волнового взаимодействия должна существенно уменьшиться. В этом случае возможность наблюдения «странного» режима, предсказанного теоретически [6] и характеризующегося срывом генерации при увеличении рабочего тока, оказывается весьма высокой.
Оротрон с ДРПС обладает широким диапазоном перестройки. Поэтому генерация возникает на более низких частотах, чем на расчётной частоте, при более низком напряжении. Отметим также, что в приборе возможно изменение связи ОР с нагрузкой за счёт смещения фокусирующего зеркала вдоль движения электронного потока относительно плоского зеркала, в котором расположен вывод энергии [7]. Изменяя положение фокусирующего зеркала можно оптимизировать связь ОР с нагрузкой и, следовательно, выходную мощность для определённого диапазона частот.
Первоначально были проведены эксперименты по исследованию диапазона перестройки оротрона с пролётным каналом 0.15мм при слабой связи ОР с нагрузкой (D=0). При этом электронный поток формировался диодной электронной пушкой с высотой катода 0.1мм и анода 0.1мм, обеспечивая заполнение канала в 0.67. Эти измерения представлены на Рис.3.
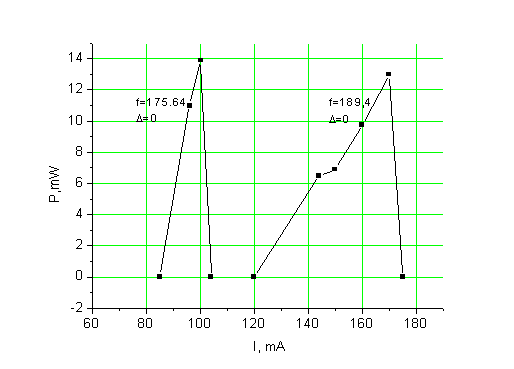
Рис.3
Как видно на Рис. 3, мощность генерации на каждой частоте при неизменном напряжении при увеличении рабочего тока сначала возрастает, а затем при достижении некоторого значения тока падает до 0. Такая картина наблюдается на всех частотах генерации в полном соответствии с предсказанием теории [6].
Затем были проведены аналогичные эксперименты при сильной связи ОР с нагрузкой (D=+1). Результаты измерений представлены на Рис.4 сплошными линиями. На этом же рисунке пунктирными линиями представлены результаты измерений для оротрона с пролётным каналом 0.1мм при той же связи ОР с нагрузкой.
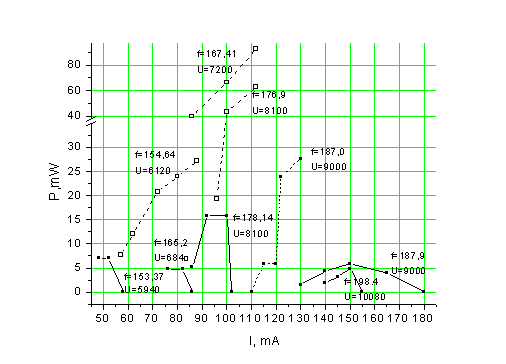
Рис. 4
Как видно на Рис.4, в случае высоты пролётного канала 0.15мм зависимость мощности генерации от тока такая же, как на Рис.3, а в случае высоты пролётного канала 0.1мм, когда эффективность электронно-волнового взаимодействия высокая (работает вся толщина электронного потока) генерируемая мощность с ростом рабочего тока только возрастает.
Заключение
Таким образом, в результате математического моделирования найден режим работы оротрона, никогда до настоящего времени не рассматривавшийся в теории и не наблюдавшийся в эксперименте. Определены условия его возникновения. Существование этого режима подтверждено экспериментом.
Следует отметить, что в силу недостаточной величины фокусирующего магнитного поля в нашем приборе получить генерацию на частоте 230ГГц не удалось, так как невозможно было провести на коллектор ток достаточной величины при соответствующем высоком напряжении.
Литература
1. Myasin Ye.A., Tseytlin M.B. at al. Study of centimeter and millimeter wave range powerful orotron’s efficient regimes at the IRE of the Academy of sciences of the USSR. //Inter. Confer.on MM Wave and Far-Infrared Science and Technology. 1992. China. Beijin. Confer. Digest. P. 94.
2. Белявский Б.А., Цейтлин М.Б. Анализ работы оротрона на основе двумерной теории. //РиЭ, 1980, Т.25, №5, С.1108-1112
3. Мясин Е. А., Соловьёв А. Н.// Оротрон с ДПС при длине волны 1 мм на первой пространственной гармонике. - 20-я Международная Крымская конференция «СВЧ-техника и телекоммуникационные технологии». 13—17сентября 2010 г. Севастополь, Крым, Украина . Материалы конференции. Т.1. С.279-280.
4. Мясин Е.А. Оптимизация оротрона с двухрядной периодической структурой на длину волны 1.3 мм на основе приближённой аналитической теории // Радиотехника и электроника. 2014. Т. 59. № 8. С.770.
5. Myasin Ye.A., Tseitlin M.B., Nutovich L. M. Analysis of the electron-wave interaction in the orotron on the basis of the approximate analytic nonlinear theory// IEEE Transactions on ED, 1990. V.37. №12. P. 2634.
6. Мясин Е.А., Андреев Ю.В. О возможном режиме генерации в оротроне с двухрядной периодической структурой терагерцового диапазона. Труды II Всероссийской Микроволновой конференции (26-28 ноября 2014 г.) г. Москва.
7. Мясин Е.А., Белявский Б.А., Соловьёв А.Н.// Патент 2274922 (РФ) Оротрон. Опубл. Б.И. 2006. № 11.