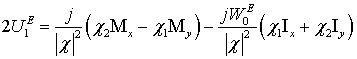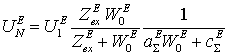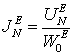Методика расчёта радиотехнических характеристик системы антенна-обтекатель
К. М. Басков, А. М. Федоренко, С. А. Федоров
ФГБУН Институт теоретической и прикладной электродинамики Российской академии наук (ИТПЭ РАН)
Статья поступила в редакцию 18 января 2016 г.
Аннотация. В статье представлена методика, основанная на принципах физической оптики, расчёта радиотехнических характеристик системы антенна – обтекатель. Эта методика сравнивается с другими существующими физико-оптическими методиками. Показывается, что точность предлагаемой методики существенно выше точности существующих методик. Приводятся результаты тестирования методики путём сравнения с расчётами в строгой постановке методом интегральных уравнений с использованием программного пакета FEKO. Также приводятся результаты расчётных и экспериментальных исследований по снижению перегиба зависимости ошибки пеленга носового осесимметричного обтекателя самолёта от угла сканирования в Н плоскости (в плоскости вектора магнитного поля). Результаты исследований, представленные в статье, были доложены на второй Всероссийской микроволновой конференции (26-28 ноября 2014, Москва).
Ключевые слова: обтекатель, диаграмма направленности, физическая оптика, ошибка пеленга.
Abstract. The paper presents a new technique, based on the principles of physical optics, for the calculation of the radio-technical characteristics of antenna – radome system with dimensions of tens of wavelengths. This method is compared with the other existing physico-optical methods. It is shown that the accuracy of the new method is significantly better than the accuracy of existing methods. The developed method was tested via comparison of results with the moment method calculations in CAD program package FEKO. Also, the results of computational and experimental studies to improve the radiotechnical characteristics of the radome are discussed. The research results presented in this article have been reported at the Second All-Russian Microwave Conference (26-28 November 2014, Moscow).
Keywords: radome, radiation pattern, physical optics, boresight error.
Введение
Для анализа влияния обтекателя на характеристики антенной системы необходимо использовать электродинамическую модель, позволяющую оценивать такие радиотехнические характеристики (РТХ), как коэффициент пропускания (КП) обтекателя, ошибку пеленга (ОП), изменение уровня боковых лепестков диаграммы направленности (ДН) антенны. Имеется достаточно много работ, в которых используются различные подходы к моделированию систем антенна – обтекатель. В [1] применён конечно – разностный метод, в [2] проиллюстрировано моделирование системы антенна – обтекатель в пакете программ FEKO, в котором для решения задачи дифракции используется метод интегральных уравнений (ИУ). Для анализа РТХ обтекателей очень больших электрических размеров используются методы геометрической оптики [3].
Для анализа систем антенна-обтекатель с размерами от 10 до 100 длин волн обычно используются методики на основе метода физической оптики [4,5,6]. Суть этих методик заключается в том, чтобы найти эквивалентные токи на внешней поверхности обтекателя или на эквивалентной апертуре, находящейся вне обтекателя, для последующего расчёта ДН антенны с обтекателем.
В [7] представлена методика точного расчёта ДН антенны с учётом многослойного магнитодиэлектрического укрытия, имеющего плоскую, цилиндрическую или сферическую форму. Метод основан на скаляризации уравнений Максвелла с помощью потенциалов Дебая для задач рассеяния электромагнитной волны слоистыми структурами из магнитодиэлектриков, который описан в [8]. В данной статье будет представлена методика, основанная на таком же подходе, расчета ДН антенны в присутствии обтекателя только произвольной формы со сложной многослойной конструкцией стенки.
1. Новая методика расчёта радиотехнических характеристик системы антенна-обтекатель
Исходя из анализа литературы, подходы, основанные на принципах физической оптики, можно разделить на три типа, именуемые далее как 1-я, 2-я и 3-я методики.
1-я методика. В [9] представлена электродинамическая модель системы антенна – обтекатель с приёмной антенной. Плоская электромагнитная волна падает на внешнюю поверхность обтекателя. В каждой точке стенка обтекателя считается локально плоской, что позволяет найти эквивалентные электрические и магнитные токи на её внутренней поверхности и далее интегрированием определить поле, принимаемое антенной. Недостаток этой модели - значительные вычислительные затраты на расчет ДН, так как для каждого направления падения волны необходимо производить интегрирование по всей поверхности обтекателя для каждой точки на поверхности антенны. В [10] предлагается способ ускорения вычислений для такой модели с использованием метода стационарной фазы.
2-я методика. В [5] рассмотрена модель системы антенна – обтекатель с передающей антенной. Как и в 1-й методике, поверхность обтекателя в каждой точке представляется локально плоской, а поле антенны в этой точке рассматривается как локально плоская волна, распространяющаяся вдоль действительной части вектора Пойнтинга. Поле с внутренней поверхности стенки пересчитывается на внешнюю поверхность обтекателя с помощью КП. Далее при расчете поля излучения интегрирование проводится по внутренней поверхности обтекателя, т.е. толщина стенки полагается нулевой. При этом КП нормируется на набег фазы, который получает фронт волны, проходя в свободном пространстве расстояние, равное толщине стенки с учётом угла падения.
3-я методика описана в [6]. В отличие от предыдущей модели внутренняя и внешняя поверхности обтекателя разнесены в пространстве на расстояние, равное реальной толщине стенки и, значит, КП не нормируется на фазовый набег волны в свободном пространстве. При таком подходе учитывается преломление волны в случае, что особенно важно, когда стенка изготовлена из плотного диэлектрика. В результате в некоторых случаях повышается точность вычисления такого важного параметра, как ОП системы антенна – обтекатель.
Основной причиной погрешностей всех выше описанных методик является предположение, что поле антенны на внутренней поверхности обтекателя является локально-плоской волной, распространяющейся вдоль действительной части вектора Пойнтинга. Часто точности этих методик не хватает, поэтому в статье предлагается новая, далее по тексту 4-я методика. Суть методики заключается в том, что на внутренней поверхности обтекателя по точным формулам рассчитывается поле излучения передающей антенны, определяются эквивалентные электрический и магнитный токи и вычисляются пространственные спектры этих токов на элементарной площадке, размеры которой намного меньше длины волны. Далее с использованием найденных спектров и аппарата длинных линий [8,11] рассчитываются спектры компонентов поля излучения на элементарных площадках внешней поверхности обтекателя и определяется ДН в дальней зоне как сумма спектров полей элементарных площадок.
Алгоритм 4-й методики представляется следующим:
1. По точным формулам рассчитывается поле антенны в каждой точке на внутренней поверхности обтекателя:
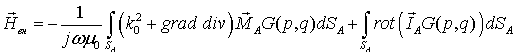 ,
,
где q - точка
интегрирования на апертуре антенны SА; p - точка
наблюдения на поверхности обтекателя; 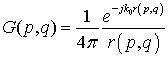 -
функция Грина свободного пространства;
-
функция Грина свободного пространства; ![]() -
расстояние от точки p до точки q; e0 и m0 –
диэлектрическая и магнитная проницаемости свободного пространства;
-
расстояние от точки p до точки q; e0 и m0 –
диэлектрическая и магнитная проницаемости свободного пространства;![]() - волновое число свободного
пространства; w - круговая частота электромагнитной волны;
- волновое число свободного
пространства; w - круговая частота электромагнитной волны; ![]() - электрический и магнитный токи на
апертуре антенны.
- электрический и магнитный токи на
апертуре антенны.
Вводятся эквивалентные токи на внутренней поверхности обтекателя как
![]() ,
,
![]() , (2)
, (2)
где
![]() - внешняя нормаль к поверхности стенки.
- внешняя нормаль к поверхности стенки.
2. В каждой точке на
внутренней поверхности обтекателя вводится локальная система координат (1x, 1y, 1z) с
осью Z, направленной вдоль ![]() (рисунок 1). Определяются величины
(рисунок 1). Определяются величины ![]() - проекции эквивалентных токов на оси
локальной системы координат. С учётом того, что на поверхности стенки обтекателя
рассматривается небольшая по сравнению с длиной волны окрестность dS точки, в пределах которой компоненты
эквивалентных токов Ix,y, Mx,y изменяются незначительно, спектры этих компонентов Ix,y и Mx,y в пространственной области
принимаются постоянными (не зависят от пространственных частот
- проекции эквивалентных токов на оси
локальной системы координат. С учётом того, что на поверхности стенки обтекателя
рассматривается небольшая по сравнению с длиной волны окрестность dS точки, в пределах которой компоненты
эквивалентных токов Ix,y, Mx,y изменяются незначительно, спектры этих компонентов Ix,y и Mx,y в пространственной области
принимаются постоянными (не зависят от пространственных частот ![]() ) и могут быть записаны в виде
) и могут быть записаны в виде
![]() ,
,
![]() .
(3)
.
(3)
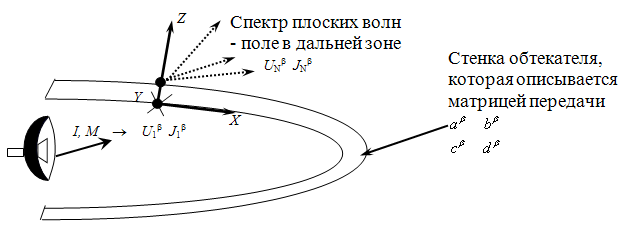
Рисунок 1 - Представление поля антенны в каждой точке на поверхности обтекателя в виде элементарного излучателя
3. Вводятся эквивалентные источники напряжения электрического и магнитного типов [8, 11] в эквивалентной схеме на рисунке 2, описывающей многослойную диэлектрическую стенку обтекателя в рассматриваемой точке
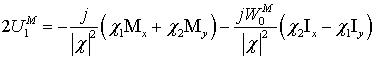 ,
,
где ![]() - пространственные частоты,
связанные с углами распространения волны
- пространственные частоты,
связанные с углами распространения волны ![]()
![]() в
локальной системе координат, которые в свою очередь могут быть найдены по
ориентации осей локальной системы координат и направлению распространения волны
во внешнем пространстве,
в
локальной системе координат, которые в свою очередь могут быть найдены по
ориентации осей локальной системы координат и направлению распространения волны
во внешнем пространстве, ![]() - волновые сопротивления
для плоских волн электрического или магнитного типов в свободном пространстве,
падающих на стенку под углом
- волновые сопротивления
для плоских волн электрического или магнитного типов в свободном пространстве,
падающих на стенку под углом ![]() .
.
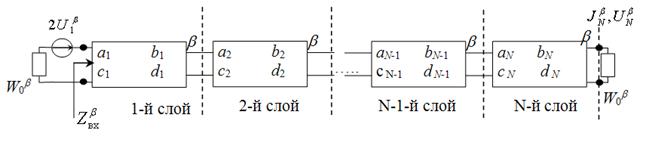
Рисунок 2 - Эквивалентная длинная линия N-слойной стенки обтекателя (b = E или М)
4. Рассчитываются токи и напряжения на выходе N- го слоя схемы на рисунке 2 по формулам:
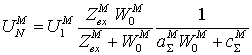 ,
, 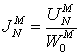 ,
,
где ![]() и
и ![]() -
элементы матрицы передачи, описывающей многослойный диэлектрик (результат произведения
матриц передачи всех слоёв стенки),
-
элементы матрицы передачи, описывающей многослойный диэлектрик (результат произведения
матриц передачи всех слоёв стенки), ![]() -входное сопротивление
длинной линии со стороны первого слоя.
-входное сопротивление
длинной линии со стороны первого слоя.
5. Зная токи и напряжения
на выходе эквивалентной длинной линии, можно найти спектры составляющих
электрического поля ![]() на внешней стороне стенки
обтекателя в локальной системе координат
на внешней стороне стенки
обтекателя в локальной системе координат
![]() ,
,
![]() ,
(6)
,
(6)
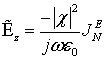 .
.
6. В итоге, зная спектр
электрического поля ![]() на внешней поверхности обтекателя, можно, не делая обратное
преобразование Фурье, сразу найти поле излучения в дальней зоне от токов на
элементарной площадке dS
на поверхности обтекателя
на внешней поверхности обтекателя, можно, не делая обратное
преобразование Фурье, сразу найти поле излучения в дальней зоне от токов на
элементарной площадке dS
на поверхности обтекателя
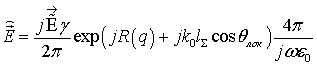 , (7)
, (7)
где ![]() ;
; ![]() ;
; ![]() - единичный вектор, определяющий направление
распространения волны в декартовой системе координат, связанной с антенной;
- единичный вектор, определяющий направление
распространения волны в декартовой системе координат, связанной с антенной; ![]() – точка интегрирования на
внешней поверхности обтекателя;
– точка интегрирования на
внешней поверхности обтекателя; ![]() - общая толщина стенки
обтекателя;
- общая толщина стенки
обтекателя; ![]() -поле в дальней зоне, нормированное на
величину
-поле в дальней зоне, нормированное на
величину ![]() .
.
В формуле (7) наличием
второго слагаемого в показателе степени экспоненты прошедшее поле нормируется
на набег фазы волны, проходящей в свободном пространстве расстояние ![]() , что позволяет совмещать внешнюю и
внутреннюю поверхности стенки обтекателя. Такое преобразование спектра полного
поля является абсолютно точным.
, что позволяет совмещать внешнюю и
внутреннюю поверхности стенки обтекателя. Такое преобразование спектра полного
поля является абсолютно точным.
7. Полное поле в дальней зоне системы антенна – обтекатель находится в виде суммы всех полей от каждой элементарной площадки на его поверхности.
8. Токи на внутренней поверхности обтекателя, обусловленные отражением электромагнитной волны от стенки, можно найти с помощью известных методов, когда поле на внутренней поверхности представляется локально-плоской волной, распространяющейся вдоль действительной части вектора Пойнтинга. Пересчитывать же поле этих токов на внешнюю поверхность обтекателя лучше с помощью предлагаемой методики по формулам (1)-(7) (необходимо повторить пункты 1-7 для поля токов, обусловленных отражением волны от стенки обтекателя).
Таким образом, в рассмотренном алгоритме использованы два приближения. Первое – неизменность компонентов эквивалентных токов Ix,y, Mx,y в пределах элементарной площадки dS, второе – замена произвольной формы стенки в каждой точке плоской структурой, параметры которой используются в формулах (5) при пересчете поля на внешнюю поверхность обтекателя (неявное применение приближения физической оптики).
Из формул (4)-(7) видно, что для определения поля в дальней зоне не требуется нахождение полей на внешней стороне стенки обтекателя, а необходимо вычислить только их спектры. Это позволяет достаточно быстро рассчитывать поле в дальней зоне в любом направлении.
2. Тестирование новой методики
Предлагаемая 4-я методика расчёта ДН антенны в присутствии обтекателя была протестирована с помощью строгого метода ИУ, реализованного в программе FEKO. Рассматривалась система антенна – обтекатель, представленная на рисунке 3. Распределение поля на апертуре антенны задавалось равномерным. Стенка обтекателя имела толщину 10 мм и диэлектрическую проницаемость равную 4,4 – j0,066. Тестирование проводилось на частоте 5 ГГц в плоскости Н, плоскости вектора магнитного поля, на границе применимости методов, основанных на принципах физической оптики, и метода ИУ. Необходимо отметить, что расчёт на суперкомпьютере одной ДН такой системы с помощью программы FEKO длился приблизительно один час, и требовалось 88 Гигабайт оперативной памяти. Расчёт с помощью предлагаемой методики, основанной на принципах физической оптики, на обычном компьютере длился не больше минуты.
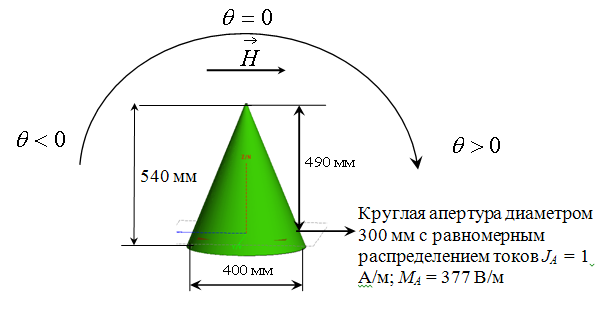
Рисунок 3 - Модель системы антенна-обтекатель в программе FEKO для тестирования новой методики
На
рисунке 4 представлены рассчитанные разными методами ДН системы
антенна-обтекатель (рисунок 3) на частоте 5 ГГц в плоскости Н при разных углах
сканирования ![]() . Погрешность в определении КП (изменение
уровня главного лепестка ДН антенны за счёт обтекателя) по 4-й методике в
сравнении с точным методом ИУ составила около 0,1 дБ. Достаточно хорошо совпали
боковые лепестки ДН до углов |q| < 500, которые связаны с искажениями фронта волны при
прохождении стенки и с отраженным от стенки полем. Погрешности в ДН, вычисленной
по 4-й методике, в секторе углов |q| > 500, связаны с тем, что в расчётах не
учитывалось вторичное отражение поля от стенки, которое в данном случае имеет
высокий уровень. Для хорошо настроенной стенки обтекателя уровень вторично
отражённого поля пренебрежимо мал. ДН, рассчитанные по 2-й методике, описанной
в [5], плохо совпадают с ДН, рассчитанными строгим методом. Погрешность в
определении КП составила более одного дБ.
. Погрешность в определении КП (изменение
уровня главного лепестка ДН антенны за счёт обтекателя) по 4-й методике в
сравнении с точным методом ИУ составила около 0,1 дБ. Достаточно хорошо совпали
боковые лепестки ДН до углов |q| < 500, которые связаны с искажениями фронта волны при
прохождении стенки и с отраженным от стенки полем. Погрешности в ДН, вычисленной
по 4-й методике, в секторе углов |q| > 500, связаны с тем, что в расчётах не
учитывалось вторичное отражение поля от стенки, которое в данном случае имеет
высокий уровень. Для хорошо настроенной стенки обтекателя уровень вторично
отражённого поля пренебрежимо мал. ДН, рассчитанные по 2-й методике, описанной
в [5], плохо совпадают с ДН, рассчитанными строгим методом. Погрешность в
определении КП составила более одного дБ.
Для рассмотренной системы антенна-обтекатель с небольшими электрическими размерами старые методики, основанные на принципах физической оптики, не подходят. Представленная методика даёт более высокую точность даже при таких небольших размерах системы.
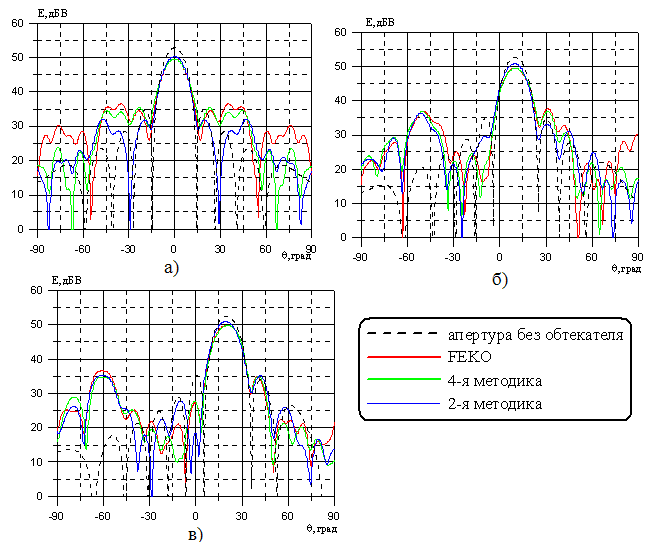
Рисунок 4 – ДН системы
антенна-обтекатель на частоте 5 ГГц в плоскости Н, рассчитанные
разными
методами при углах сканирования а) qс
= 00; б) qс = 100
и в) qс = 200
К сожалению, для модели с малыми электрическими размерами с помощью 4-й методики не удаётся с достаточной точностью определить такую важную характеристику как вносимая ОП (смещение равносигнального направления разностной ДН антенны за счёт обтекателя). На рисунке 5 представлены вычисленные разностные ДН этой же системы антенна-обтекатель на частоте 5 ГГц в плоскости Н. Для систем с размерами меньше десяти длин волн, у которых антенна имеет широкую ДН, 4-я методика даёт существенную погрешность (около 20 угловых минут) при определении ОП, хотя общий вид разностных ДН достаточно хорошо совпадает. Погрешность связана не только с тем, что размеры системы малы, но и с тем, что радиус кривизны обтекателя соизмерим с толщиной стенки. С увеличением электрических размеров и при уменьшении толщины стенки относительно радиуса кривизны обтекателя погрешность будет уменьшаться.
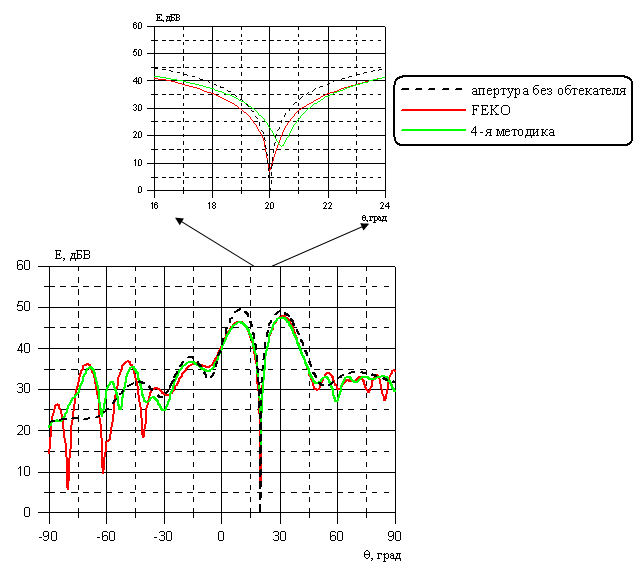
Рисунок 4 – ДН системы
антенна-обтекатель на частоте 5 ГГц в плоскости Н, рассчитанные
разными
методами при углах сканирования а) qс
= 00; б) qс = 100
и в) qс = 200
3. Экспериментальная проверка точности новой методики
Точность предлагаемой 4-й методики оценивалась при сравнении результатов расчётов и измерений ДН реального носового осесимметричного обтекателя летательного аппарата с оживальной образующей (рисунок 6). Обтекатель имел оптимальную стенку многослойной конструкции из слоёв стеклопластика. Антенна, моделировалась круглой апертурой диаметром 900 мм, на которой в расчетах задавалось амплитудно-фазовое распределение поля максимально приближенное к распределению для реальной антенны. Подбор амплитудно-фазового распределения поля на апертуре проводился по результатам измерений по методике, описанной в [12]. На рисунке 7 представлены измеренные и рассчитанные с помощью 2-й и 4-й методик ДН антенны с обтекателем в плоскости Н на верхней частоте рабочего диапазона, где вблизи главного лепестка наблюдаются заметные искажения ДН, обусловленные наличием обтекателя. Можно заметить, что для таких размеров систем обе методики позволяют достаточно точно рассчитывать ДН, но всё-таки 4-я методика даёт результат, более близкий к эксперименту.
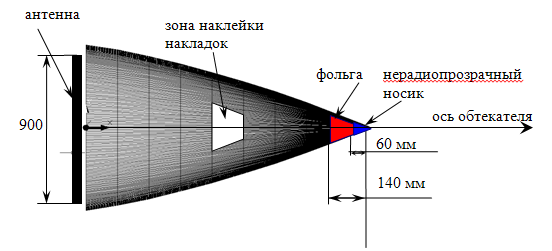
Рисунок 6 – Носовой осесимметричный обтекатель
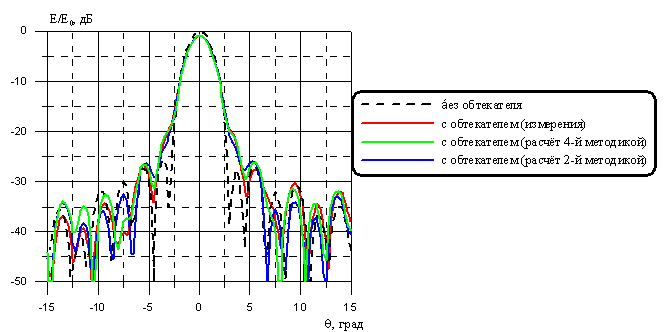
Рисунок 7 – ДН антенны с обтекателем (рисунок 6) в плоскости Н на верхней частоте рабочего диапазона
Предлагаемая методика является очень полезным и удобным инструментом для решения радиотехнических задач, связанных с обтекателями. Так, для обтекателя на рисунке 6 была поставлена задача выяснить причину и избавиться от перегиба в зависимости ОП от угла сканирования (пеленгационная характеристика) вблизи оси обтекателя в плоскости Н. Сначала были проведены расчёты, которые дали возможность правильно поставить дорогостоящий эксперимент. Расчёты по старым методикам давали существенные погрешности в определении ОП, что не позволяло их использовать для постановки эксперимента. Рассматривались три варианта комплектации обтекателя: 1-й вариант – обтекатель в исходном виде; 2-й вариант – обтекатель с увеличенным до 140 мм с помощью фольги нерадиопрозрачным носиком; 3-й вариант – обтекатель с двумя диэлектрическими накладками, наклеенными в определённые зоны (рисунок 6) на внутренней поверхности стенки. Зоны наклейки накладок оптимизировались с помощью расчётов. На рисунках 8а, б и в представлены измеренные и рассчитанные с помощью 4-й методики зависимости ОП от угла сканирования в плоскости Н для 3-х вариантов комплектации обтекателя на средней частоте рабочего диапазона. Из сравнения зависимостей ОП от угла сканирования 1-го и 2-го вариантов (рисунки 8 а и б) становится понятно, что величина перегиба пеленгационной характеристики зависит от размера нерадиопрозрачного носика. При увеличении его размера перегиб увеличился в два раза с 1,5 до 3 угловых минут. После наклейки диэлектрических накладок величина перегиба составила 0,5 угловых минут (рисунок 8в), при этом другие характеристики обтекателя (КП, изменения уровня боковых лепестков ДН) практически не изменились.
Если обратить внимание на расчётные пеленгационные характеристики (пунктирные линии на рисунках 8), то можно увидеть, что они имеют небольшие изломы. Эти изломы связаны с погрешностями при вычислении полей в дальней зоне от токов на участках поверхности обтекателя, которые находятся на границе “свет-тень”. Также эти погрешности наблюдаются в виде высокого уровня боковых лепестков при вычислении ДН в тех направлениях, в которых излучение с достаточно большой части поверхности обтекателя идёт под скользящими углами. Погрешность расчётов при углах наблюдения, близких к границе “свет-тень”, которая также была отмечена в работе [12], является недостатком 4-й методики, который надо учитывать при проведении расчётов.
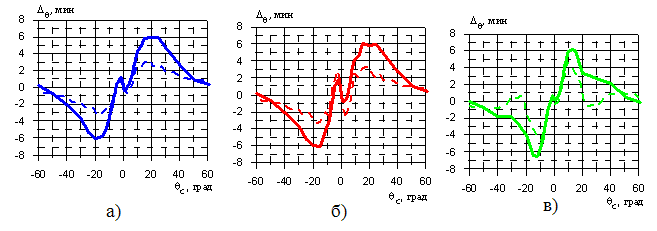
Рисунок 8 – Зависимости ОП от угла
сканирования носового обтекателя в Н плоскости
на средней частоте рабочего
диапазона для трёх вариантов комплектации:
а) 1 вариант; б) 2 вариант и в) 3
вариант (сплошные линии – измерения,
пунктирные линии - расчёт)
Заключение
Разработанная методика расчёта РТХ системы антенна – обтекатель, основанная на принципах физической оптики, позволяет с высокой точностью рассчитывать поле излучения антенны в дальней зоне с учётом обтекателя с многослойной диэлектрической стенкой. Главным преимуществом предлагаемой методики перед другими методиками, основанными на принципах физической оптики, является то, что она сохраняет точность расчётов ДН систем с размерами меньше десяти длин волн.
Проведённые тесты показали, что предлагаемая методика позволяет быстро и с высокой точностью рассчитывать РТХ обтекателя любой формы, размера и с произвольной конструкцией диэлектрической стенки. Кроме этого, учитывается преломление волны при прохождении стенки, что позволяет точно рассчитывать ОП для больших систем антенна - обтекатель. Предлагаемая методика легко может быть модернизирована для случая, когда стенка обтекателя содержит дифракционную решётку.
К недостаткам предлагаемой методики следует отнести существенную погрешность при вычислении ДН антенны с обтекателем в направлениях, при которых большая часть его поверхности находится под скользящими углами.
Литература
1. Бойко М.А., Титов А.Н., Ястребов В.П. “Обтекатели РЛС самолетов нового поколения” // Радиотехника, 2002, № 11.
2. Кисель Н. “Моделирование системы антенна обтекатель в пакете программ FEKO” // Современная электроника, 2011, № 9.
3. Князева Л.В. “Методы расчета характеристик системы антенна – обтекатель” // Антенны, 1998, № 1.
4. Абрамов В.В., Каплун В.А. “Расчёт диаграмм направленности антенн при наличии диэлектрических оболочек” // Вопросы радиоэлектроник, 1971, выпуск 22.
5. Wu D.C.F., Rudduck R.C. “Plane wave Spectrum-Surface integration technique for Radome analysis” // IEEE Transactions on Antennas and Propagation, 1974, №5, May.
6. Uno T., Adachi S., Sawaya K. “Three-dimensional computational analysis of Radomes” // Radio Science, 1987, vol. 22, №6, November, pp. 913-916.
7. Суркова И.В. “Влияние многослойных диэлектрических укрытий различной конфигурации на характеристики антенн с плоской апертурой” / Диссертация на соискание учёной степени кандидата технических наук – Москва, 1994.
8. Бодров В.В., Сурков В.И. “Математическое моделирование устройств СВЧ и антенн” Учебное пособие – Москва: Издательство МЭИ, 1994 год.
9. Kazimierz Siwiak, Thomas B. Dowling, Lawrence R. Lewis “Boresight Errors Induced by Missile Radomes” // IEEE Transactions on Antenna and Propagation, 1979, vol. AP-27, № 6, November.
10. Колосов Ю.А., Левков Ф.Е. “Об использовании метода стационарной фазы в экспресс – оценке влияния обтекателя на параметры антенны” // Антенны, 2012, №1.
11. Бодров В.В., Романов С.И. “Учёт влияния плоскослоистой среды на характеристики вибраторных антенн” // Радиотехника и электроника, 1998, т. 43, № 10.
12. Басков К.М., Бобков Н.И., Краснолобов И.И., Семененко В.Н. “Моделирование сверхширокополосной зеркальной антенны” // Журнал радиоэлектроники [электронный журнал], 2013, № 4. URL: http://jre.cplire.ru/jre/apr13/9/text.html
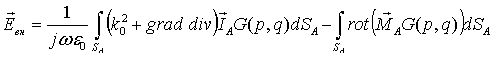 ; (1)
; (1)