Анализ двумерно-периодической волноводно-щелевой решетки с частотно-фазовым сканированием луча

 

В. И. Калиничев¹, А. А. Бабаскин^2
1 ИРЭ им. В. А. Котельникова РАН
² RF Mtech, Сеул, Юж. Корея

 

Статья поступила в редакцию 2 февраля 2016 г.

 

Аннотация. Предложена модель для численного анализа постоянной распространения вытекающей моды в двумерно-периодической решетке из прямоугольных волноводов со щелями в широкой стенке. Рассчитаны частотные зависимости действительной и мнимой частей постоянной распространения для разных фазовых сдвигов между соседними волноводами. Приведено сравнение с постоянной распространения вытекающей моды в линейной одномерной решетке. Показано, что частотные зависимости фазовой постоянной и постоянной затухания имеют особенности при  определенных фазовых сдвигах. Рассчитаны угловые координаты луча в пространстве и диапазон сканирования при изменении частоты и фазового сдвига в рассмотренных пределах.

Ключевые слова. Антенные решетки, волноводы со щелями, вытекающая мода, двумерное сканирование.

Abstract. A model is proposed for the numerical analysis of the propagation constant of the leaky mode in a dual-periodic array of rectangular waveguides with slots in the broad wall. The real and imaginary parts of the propagation constant depending on the frequency are computed for different phase shifts between adjacent waveguides. Comparison with the propagation constant of the leaky mode in the linear one-dimensional array is given. It is shown that the frequency dependences of the phase and attenuation constants have specific features at certain phase shifts. The angular coordinates of the beam in space and the 2D scanning range are calculated with changing the frequency and phase shift in the considered bounds.

Keywords:  antenna arrays, slotted waveguides, leaky mode, 2D beam scanning.

 

Введение

Планарные двумерно-периодические антенные решетки на щелевых волноводах представляют интерес с точки зрения построения антенн с двумерным частотно-фазовым сканированием луча.  Обзоры волноводно-щелевых решеток, методы их анализа и проектирования, включающие аналитические и численные методы, содержатся в  [1-7]. Некоторые приложения таких решеток в многолучевых устройствах представлены в [8-12].

 

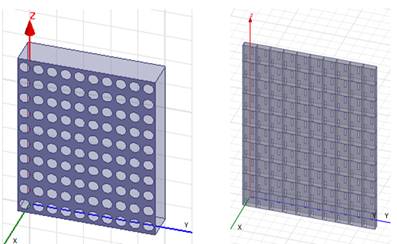
а                                              б

Рис. 1. Двумерно-периодические решетки: (а) в экране планарного волновода,
(б) решетка прямоугольных волноводов со щелями в широкой стенке

Можно выделить  два характерных типа двумерно-периодических планарных решеток, показанных на рис. 1: решетка отверстий-щелей в экране планарного волновода (а) и решетка прямоугольных волноводов со щелями в широкой стенке (б). Антенны с двумерным сканированием можно строить на основе решеток обоих типов.  В решетке типа (а) волна не имеет ограничений на направление распространения в виде внутренних металлических стенок и может распространяться под любым углом относительно некоторой выделенной оси. При равенстве периодов вдоль осей Z и Y структура является практически изотропной по направлению распространения. В отличие от нее, в решетке из волноводов типа (б) имеется выделенное направление распространения волн внутри решетки вдоль оси волноводов (ось Z). В этом смысле она является существенно более анизотропной по сравнению с решеткой (а) и представляет совокупность взаимодействующих по внешнему пространству отдельных линейных решеток. Печатным аналогом решетки (б) является антенная решетка из интегральных волноводов, стенки которых образованы системой сквозных металлизированных отверстий в подложке, a щели прорезаны в верхней металлизации подложки. В зарубежной литературе для таких волноводных структур используется термин substrate integrated waveguides (см., например, [11]).

Для получения узкого луча с большим усилением необходимо использовать большие по размеру решетки с большим числом периодов вдоль обоих направлений периодичности. Для определения характеристик большой конечной решетки естественно воспользоваться идеализированной моделью бесконечной двумерно-периодической решетки. В рамках этой модели можно пытаться рассчитать постоянную распространения собственной излучающей моды и направление излучения при задании произвольных фазовых сдвигов в обоих направлениях периодичности. Для расчета постоянной распространения в щелевом прямоугольном волноводе в [13] предложена модель, основанная на выделении ячейки-периода и использовании периодических граничных условий. В [14] этот метод используется для решения задачи синтеза антенны вытекающей волны на прямоугольном волноводе с эквидистантной решеткой двойных щелей переменной длины в широкой стенке и с синусоидальным распределением поля вдоль волновода. Что касается двумерно-периодических решеток, в [13] содержится пример численного расчета постоянной распространения для планарной решетки типа (а) с отверстиями в верхнем экране. В этом случае выделяется ячейка решетки и используются периодические граничные условия на двух парах границ ячейки вдоль  осей Z и Y, включая части границ внутри волновода, с фазовыми сдвигами, зависящими от направления распространения волны в планарном волноводе. В случае решетки типа (б) с направлением распространения вдоль оси волноводов метод расчета постоянной распространения вытекающей волны в ней, в основном, аналогичен. Однако при этом периодические граничные условия на границах ячейки, ограничивающих ее размер вдоль оси Y, задаются только на части границ в области над решеткой в виде фазового сдвига, равного сдвигу фазы в соседних волноводах решетки. В такой модели учитывается более сложный механизм распространения вытекающей волны в решетке волноводов, при котором фаза волны внутри волноводов изменяется вдоль оси Z, а фаза волны в области над решеткой изменяется в направлении под углом к оси Z. Величина этого угла зависит от отношения сдвига фазы на периоде вдоль оси Z к сдвигу фазы на периоде вдоль оси Y.

Естественно, в модели бесконечной двумерно-периодической решетки не могут быть учтены края решетки и их влияние на характеристики излучения конечной решетки.  Однако можно предполагать, что расчет постоянной распространения вытекающей моды при использовании модели бесконечной решетки позволяет достаточно точно определить направление излучения в решетке конечных размеров. Подтверждение соответствия углов излучения, определенных на основе постоянной распространения в бесконечной решетке и путем решения задачи возбуждения конечной решетки, содержится ниже в разделе 2. Цель данной работы - предложить метод расчета и провести численный анализ постоянной распространения, а также угла излучения вытекающей моды в двумерно-периодической решетке волноводов со щелями (рис. 1б) в зависимости от частоты и фазового сдвига между соседними волноводами.

1.                Модель и анализ постоянной распространения

Для вычисления постоянной распространения вытекающей моды в двумерной решетке на рис. 1б будем использовать модель на рис. 2, аналогичную предложенной в [13] для решетки на рис. 1а. Выделяем ячейку структуры с размерами, равными периодам вдоль  Z и Y, и используем периодические граничные условия на двух парах ее границ. Причем на границах, ограничивающих ячейку вдоль оси Y, периодические условия ставятся только на той части границ, которая расположена в пространстве над решеткой. На части границ внутри волновода используются обычные граничные условия нуля тангенциальной компоненты напряженности электрического на узких стенках волновода. Кроме того, как и в [13], в данной модели используем согласующий слой (по определению perfect matched layer (PML)), расположенный на некотором расстоянии от широкой стенки со щелями, через которые происходит излучение вытекающей моды. Контур границы раздела PML - воздух обозначен голубой линией внутри ячейки на рис. 2.

 

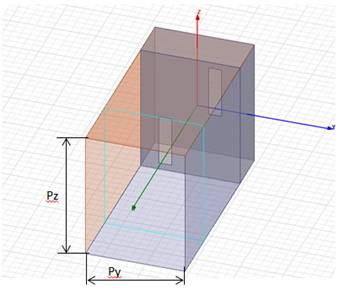
Рис. 2. Модель ячейки двумерно-периодической решетки на рис. 1б с двумя парами
периодических граничных условий на двух парах граней вдоль Z и вдоль Y
и с PML слоем на некотором расстоянии от широкой стенки со щелями

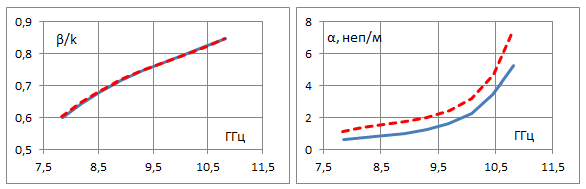
Задавая фазовый сдвиг Φy на периоде в поперечном направлении вдоль Y как параметр, будем находить действительную и мнимую части постоянной распространения в зависимости от фазового сдвига на периоде вдоль продольной оси Z. В такой постановке на основе метода [13] можем рассчитать дисперсионные характеристики вытекающей волны  в бесконечной двумерной решетке при разных значениях сдвига фазы Φy между соседними волноводами. На рис. 3 представлены рассчитанные частотные зависимости фазовой постоянной распространения и постоянной вытекания волны в решетке для нескольких значений Φy от 0 до 150° с шагом 30° для волновода с бесконечно-тонкими идеально проводящими стенками. Период вдоль оси Z задан Pz=30 мм, период вдоль Y равен размеру широкой стенки волновода Py=23 мм, длина и ширина щелей заданы соответственно 12 мм и 3 мм. Для сравнения пунктирные линии на этих графиках показывают соответствующие зависимости для одномерной линейной решетки на уединенном волноводе. Значение Φy=0 относится к случаю синфазной двумерной решетки. Видим, что при сравнительно небольших фазовых сдвигах Φy постоянная затухания в линейной решетке превышает аналогичную величину для двумерной синфазной решетки. При увеличении Φy величина затухания для двумерной решётки растет, и при достаточно больших фазовых сдвигах (Φy=150° на рис. 3) постоянная затухания в двумерной решетке может быть выше, чем в одномерной. Особенности в частотных зависимостях постоянной распространения и вытекания, представленных на рис. 3, возникают на частотах, при которых начинает выполняться условие для распространения -1 пространственной гармоники, связанной с периодичностью вдоль оси Y. Это имеет место при условии (Φy-2π)/Py = -k, где Py – период вдоль Y, k = 2π/λ – волновое число в свободном пространстве на заданной частоте. При Φy=60° это условие выполняется на частоте 10.8 ГГц, при Φy=90° - на частоте 9.6 ГГц, при Φy=120° - на частоте 8.8 ГГц. При Φy=150° левая часть по модулю меньше волнового числа k во всем рассмотренном диапазоне частот > 7.8 ГГц. Это означает, что при таком сдвиге фазы условие для распространения и излучения -1 пространственной гармоники вдоль оси Y выполняется при всех рассмотренных в данном расчете частотах. Для удобства сравнения  на рис. 4 а, б на одном графике представлены фазовая постоянная и постоянная вытекания в решетке с разными значениями Φy. Пунктирные линии соответствуют характеристикам для линейной решетки на щелевом волноводе с бесконечно тонкой стенкой. Более детальный анализ дисперсионных характеристик в окрестности частот, на которых возникает -1 пространственная гармоника по Y, не входит в задачу данной работы.

 

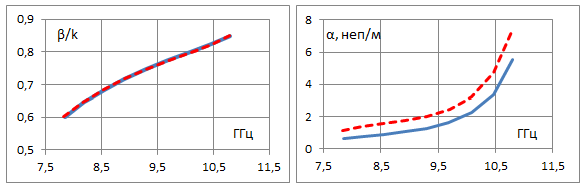
Φy=0

Φy=30°

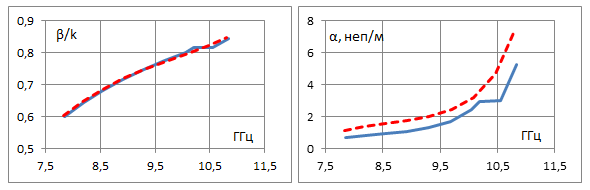
Φy=60°

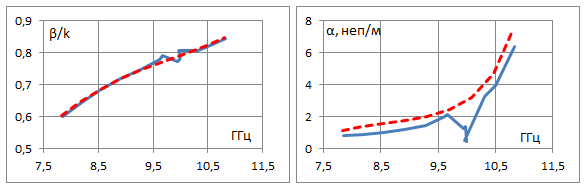
Φy=90°

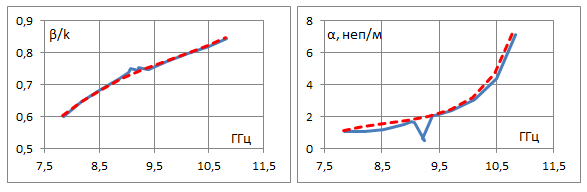
Φy=120°

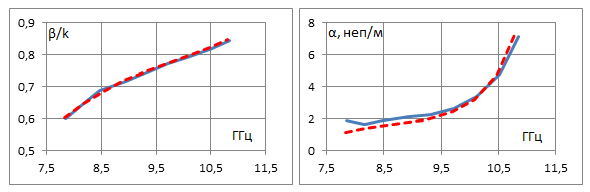
Φy=150°

 Рис. 3. Действительная и мнимая части постоянной распространения  вытекающей моды
 в двумерно-периодической решетке волноводов с продольными щелями в широкой стенке
в зависимости от частоты при разных фазовых сдвигах между соседними волноводами

 

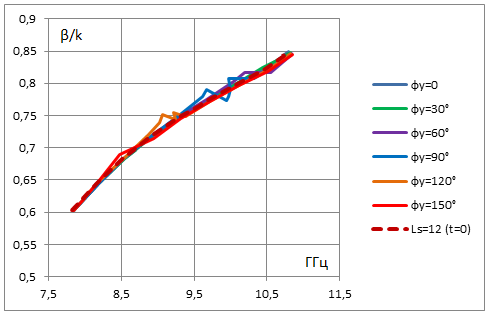
а

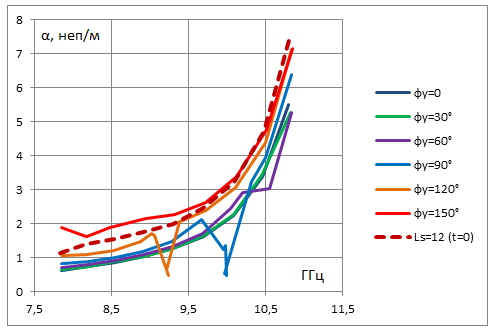
б

Рис.4. Сравнение фазовой постоянной (а) и постоянной затухания (б) вытекающей моды
 в зависимости от частоты при разных фазовых сдвигах между соседними волноводами

 На рис. 5 представлены распределения поля вытекающей моды  в трех ортогональных плоскостях внутри ячейки двумерно-периодической решетки. Наглядно проявляются наклоны фазового фронта в области над решеткой в плоскостях XY и ZX, в данном случае при сдвиге фаз Φy=60° между соседними волноводами.

 

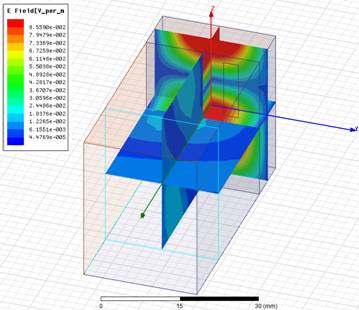
Рис. 5. Распределения амплитуды электрического и магнитного полей в
 ячейке для вытекающей моды на частоте 8.907 ГГц при  фазовом сдвиге 60°

2.                Направление излучения

По результатам расчета постоянной распространения на рис. 6 построены частотные зависимости угла излучения вытекающей моды в сферической системе координат с осью, направленной по нормали к плоскости решетки (ось X), см. рис. 1б. Параметром является фазовый сдвиг между соседними волноводами. В данной системе координат угол θ₀ - угол места, отсчитываемый от оси X, в плоскости, содержащей направление максимального излучения. Угол φ₀ – азимутальный угол, отсчитываемый в плоскости решетки ZY от оси - Z в направлении оси +Y, которой соответствует φ₀= 90°. Отрицательные значения θ₀ на рис. 6а соответствуют тому, что излучение волны происходит  на -1 пространственной гармонике, связанной с периодичностью по Z, в заднее полупространство относительно направления распространения волны вдоль положительного направления оси Z. Положительные значения φ₀ на рис. 6б соответствуют направлению излучения 0-ой пространственной гармоники, связанной с периодичностью вдоль Y. При синфазном возбуждении волноводов (Φy=0) угол φ₀ равен 0 независимо от частоты, так как при этом направление максимального излучения лежит в плоскости XZ. Таким образом, углы θ₀, φ₀ на рис. 6 соответствуют лучу, который формируется излучением на -1 пространственной гармонике по Z и на 0-ой пространственной гармонике по Y. Как и следовало ожидать, при увеличении сдвига фаз между волноводами отклонение луча от плоскости XZ возрастает (растет угол φ₀). Кроме того, при этом растет также отклонение луча от нормали (растет абсолютная величина θ₀). Следует отметить, что отклонение луча от нормали растет с понижением частоты для всех рассмотренных величин фазового сдвига между волноводами. И, наоборот, с повышением частоты угол излучения приближается к нормали. Как отмечалось выше, при наличии сдвига  фазы между соседними волноводами на определенной частоте в рассмотренном частотном диапазоне может возникать и распространяться  -1 гармоника по Y, которой соответствует другой пространственный луч. Этот луч, формируемый -1 гармоникой по Z и -1 гармоникой по Y, в данном диапазоне частот может быть сравним и даже превосходить по амплитуде луч на 0-ой гармонике по Y. Таким образом, при изменении частоты и фазы между волноводами при определенных условиях может наблюдаться режим  излучения двух сравнимых по амплитуде лучей. При дальнейшем росте частоты по мере возникновения и распространения новых высших пространственных гармоник число лучей может быть больше двух. В представленных на рис. 6 зависимостях наглядно проявляется эффект двумерного частотно-фазового сканирования в рассматриваемой двумерно-периодической решетке из прямоугольных волноводов.

 

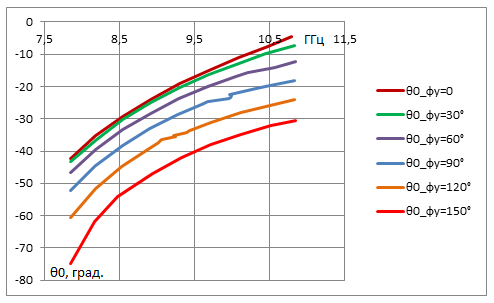
а

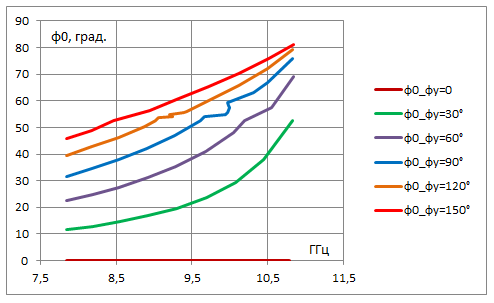
б

Рис. 6. Частотные зависимости направления излучения волны в двумерно-периодической решетке для разных фазовых сдвигов между соседними волноводами: а – угол места, б – азимутальный угол. Пространственная гармоника -1 (по Z), 0 (по Y)

Для подтверждения рассчитанных выше значений угла излучения на основе расчета постоянной распространения собственной вытекающей моды в бесконечной двумерно-периодической решетке была составлена модель фрагмента из 10 волноводов 23х10 мм. Каждый волновод имеет одинаковую решетку щелей с длиной вдоль Z, равной 10 периодам щелевой структуры. Таким образом, полный размер щелевой апертуры данной двумерной решетки 300х230 мм. Предполагаем, что все волноводы возбуждаются с одинаковой амплитудой, в то время как фазовый сдвиг между волноводами может меняться по линейному закону. Подробный анализ характеристик такой решетки при разных амплитудно-фазовых распределениях на входах волноводов является предметом отдельной работы. Здесь нас интересует только направление излучения волны в решетке при разных фазовых сдвигах Φy между соседними волноводами. Рассчитанные с помощью метода конечных элементов в рамках данной модели углы максимального излучения (θ_м, φ_м) в сферической системе координат для разных значений Φy от 0 до 150° на частоте 9.5 ГГц представлены в таблице 1. Там же для сравнения приведены углы (θ₀,  φ₀), рассчитанные выше и представленные на рис. 6. Следует еще раз отметить, что содержащиеся в таблице угловые координаты соответствуют направлению луча за счет излучения -1 пространственной гармоники по Z и 0-й гармоники по Y. 

Таблица 1. Углы максимального излучения в градусах для разных фазовых сдвигов между волноводами на частоте 9.5 ГГц

Φy,°	θм	φм	θ0	φ0
0	-17	0	-17	0
30	-18	21	-18	22
60	-22	38	-22	38
90	-26	49	-26	50
120	-32	56	-33	57
150	-40	62	-40	63

 

Видим, что значения углов, полученные из решения задачи на собственные значения, отличаются от соответствующих значений в  задаче возбуждения фрагмента из 10 волноводов не более чем на градус. Это отличие лежит в пределах погрешности вычисления диаграммы направленности в методе конечных элементов с заданным разрешением 1° по обеим угловым координатам θ и φ. Сравнение значений углов в таблице 1 может служить подтверждением справедливости использования модели бесконечной решетки для определения направления излучения в конечной решетке. Также это подтверждает результаты расчета постоянной распространения вытекающей моды в двумерно-периодической решетке.

Заключение

Рассмотрена задача распространения и излучения вытекающей моды в двумерно-периодической волноводно-щелевой решетке для случая линейного сдвига фазы между волноводами, образующими решетку. Показано, что при сравнительно небольших фазовых сдвигах между соседними волноводами постоянная затухания вытекающей моды в рассмотренной двумерно-периодической  решетке меньше, чем в отдельной линейной решетке. При увеличении фазового сдвига величина затухания в двумерной решетке растет, и при достаточно больших сдвигах фазы начинает превосходить затухание в одномерной решетке. Отмечены особенности фазовой характеристики и постоянной затухания в окрестности частоты возникновения -1 пространственной гармоники, обусловленной периодичностью в направлении, перпендикулярном осям волноводов. Путем сравнения с решением задачи возбуждения конечной решетки показано, что на основе рассчитанных значений постоянной распространения вытекающей моды в бесконечной двумерно-периодической решетке удается достаточно точно (до одного градуса) предсказать направление излучения в конечной решетке больших размеров. Результаты могут быть использованы при анализе и проектировании антенных решеток вытекающей волны с двумерным сканированием луча. Характерной особенностью рассмотренной решетки на полых прямоугольных волноводах является сканирование луча в заднем полупространстве относительно направления распространения волны в волноводах. Одним из способов расширения диапазона сканирования и включения в него углов излучения в переднем полупространстве может быть  использование щелевых волноводов с диэлектрическим заполнением.

Авторы выражают благодарность В. А. Калошину за постановку задачи и обсуждение результатов работы.

Литература

1. К. Уолтер. Антенны бегущей волны. Пер. с англ. под ред. А. Ф. Чаплина. М.: Энергия, 1970.

2. R. J. Mailloux. Phased array antenna handbook, Artech House, 1994, Norwood, MA.

3. В. А. Калошин. Антенны миллиметровых волн. Зарубежная радиоэлектроника, 1984, №11, с.97-106.

4. М. Б. Мануилов, В. А. Лерер, Г. П. Синявский. Методы расчета и новые применения волноводно-щелевых антенных решеток. Успехи современной радиоэлектроники, 2007, №5, с. 3-28.

5. M. Manuilov, V. Lerer, G. Sinyavsky. Fast and Accurate Full-Wave Analysis of Large Slotted Waveguide Array Antennas. Proc. of 37th Eur. Microw. Conf., Oct 2007, pp. 360–363.

6. С. Е. Банков. Антенные решетки с последовательным питанием. М.: Физматлит, 2013.

7. F. Xu and K. Wu. Understanding Leaky-Wave Structures. IEEE Microwave Magazine, July/Aug. 2013, vol. 14, No. 5, p. 87-96.

8. Y. J. Cheng, W. Hong, and K. Wu. Millimeter-Wave Substrate Integrated Waveguide Multibeam Antenna Based on the Parabolic Reflector Principle. IEEE Trans. on Antennas and Propagation, 2008, vol. 56, No. 9, p. 3055-3058.

9. M. Ettorre, A. Neto, G. Gerini, and S. Maci. Leaky-Wave Slot Array Antenna Fed by a Dual Reflector System, IEEE Trans. on Antennas and Propagation, 2008, vol. 56, No. 10, p. 3143-3149.

10. Y. J. Cheng, et al. Substrate Integrated Waveguide (SIW) Rotman Lens and Its Ka-Band Multibeam Array Antenna Applications. IEEE Trans. on Antennas and Propagation, 2008, vol. 56, No. 8, p. 2504-2513.

11. P. Chen, et al. A Multibeam Antenna Based on Substrate Integrated Waveguide Technology for MIMO Wireless Communications, IEEE Trans. on Antennas and Propagation, 2009, vol. 57, No. 6, p.1813-1821.

12. M. Ettorre, R. Sauleau, and L. Le Coq. Multi-Beam Multi-Layer Leaky-Wave SIW Pillbox Antenna for Millimeter-Wave Applications. IEEE Trans. on Antennas and Propagation, 2011, vol. 59, No. 4, p. 1093-1100.

13. В. И. Калиничев, А. А. Бабаскин. Метод расчета постоянной распространения вытекающей моды в волноводах со щелями. Журнал радиоэлектроники, 2015, №7. http://jre.cplire.ru/jre/jul15/2/text.pdf

14. В. И. Калиничев. Анализ и синтез волноводно-щелевой антенны с заданным амплитудным распределением. // Журнал радиоэлектроники: электронный журнал.  2015. №12. URL: http://jre.cplire.ru/jre/dec15/8/text.pdf